Back to Journals » Drug Design, Development and Therapy » Volume 17

Editorial

Statistical Analysis in Clinical and Experimental Medical Research: Simplified Guidance for Authors and Reviewers

       

Authors Panos GD , Boeckler FM 

Received 24 June 2023

Accepted for publication 30 June 2023

Published 3 July 2023 Volume 2023:17 Pages 1959—1961

DOI https://doi.org/10.2147/DDDT.S427470

Checked for plagiarism Yes

Download Article [PDF] 


Georgios D Panos,1,2 Frank M Boeckler3,4

1Department of Ophthalmology, Queen’s Medical Centre, Nottingham University Hospitals NHS Trust, Nottingham, UK; 2Division of Ophthalmology and Visual Sciences, School of Medicine, Faculty of Medicine and Health Sciences, University of Nottingham, Nottingham, UK; 3Department of Pharmacy and Biochemistry, Eberhard Karls Universität Tübingen, Laboratory for Molecular Design and Pharmaceutical Biophysics, Institute of Pharmaceutical Sciences, Tübingen, 72076, Germany; 4Institute for Bioinformatics and Medical Informatics (IBMI), Eberhard Karls Universität Tübingen, Tübingen, 72076, Germany

Correspondence: Georgios D Panos, Department of Ophthalmology, Eye & ENT Centre, Queen’s Medical Centre, Derby Road, Lenton, Nottingham, NG7 2UH, UK, Tel +44 115 924 9924, Email [email protected]

There has been a growing emphasis in recent years on the importance of statistical analysis in medical research. Accurate statistical analysis is essential for ensuring the validity and reliability of research findings, as well as experiment reproducibility. However, many researchers may not have a strong background in statistics, which can lead to problems with study design, data analysis, and result interpretation.

The main takeaway from our extensive editorial experience is that basic statistical rules are not routinely followed by the authors, including extremely small group size, data distribution assessment, inappropriate use of parametric tests and pseudoreplication, and this is missed during the peer review process.

To address this issue we are, hereby, providing guidance for authors and peer reviewers on medical statistics. These guidelines provide a helpful framework for the researchers to follow when designing studies and analysing data, and for the reviewers to use when assessing the quality and accuracy of the manuscripts. Our authors are kindly requested to provide a detailed data and statistical analysis paragraph within the Methods section to facilitate the implementation of these guidelines.

  • 1. Although there is no universally defined minimum group size, group sizes must be large enough to allow for meaningful statistical analysis. For datasets undergoing statistical analysis, we have established a minimum “n” of 5 independent observations per group. If carefully justified (eg, limited sample availability, medico-legal reasons, etc.), it is acceptable to design a study to compare groups with “n” below 5; however, in this case, no statistical analysis should be performed, the findings must be presented as preliminary and authors should discuss this limitation in their manuscript.An alternative option to handle very small groups (n < 5) is the permutation and bootstrap tests that do not rely on distributional assumptions.1–3
  • a) For randomised clinical trials and prospective clinical studies, researchers are required to conduct power calculations based on the anticipated effect size, desired level of significance (typically 0.05), and desired statistical power (must be 80% or higher), to determine the appropriate sample size.4,5
  • b) The “resource equation method” offers an alternative approach to determine sample sizes, taking into account the law of diminishing returns. This method proves particularly valuable for biological experiments and animal studies involving multiple treatment groups with small sample size that require analysis through analysis of variance (ANOVA). In such cases, conducting a power analysis becomes challenging.6,7 The “resource equation method” establishes the acceptable range for error degrees of freedom, in an ANOVA, between 10 and 20.

    • The case can be simplified to the following equation: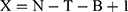

    N = total number of observations,

    T = number of treatments,

    B = number of blocks

    X = should be between 10 and 20.

  • 2. Authors should use groups of equal size when the number of observations (sample size) is n < 20 per group, to maximise statistical power and minimise bias and error variance.
  • 3. Each group should consist of independent observations. In clinical studies, it is a common mistake to include both sides (eg, both eyes) of the same patient and analyse these data with traditional statistics (ie, ANOVA, t-test, etc.). Including both sides of the same subject violates the assumption of the independence of observations, and therefore traditional statistical tests are not appropriate. Authors should either choose one side of each patient or (if it is necessary to include both sides to minimise waste of data) use more advanced statistics such as mixed-effects models and generalised estimating equations to account for within-subject and between-subject variability.8–10Similarly, in experimental studies, pseudoreplication must be avoided.11 One sample run three times (“in triplicate”) is n = 1 and not n = 3. Pseudoreplication is not acceptable in Drug Design Development and Therapy and can only be used to test the reliability of single values. Our authors are kindly advised to check the Partnership for Assessment and Accreditation of Scientific Practice (PAASP GmbH) website for further instructions on how to avoid pseudoreplication in their experiments.12
  • 4. Authors should assess data distribution and homogeneity before conducting any statistical analysis. Applying parametric tests when the data are skewed is not acceptable, unless the sample size is large and the data do not deviate significantly from normality. We recommend that authors use the Shapiro–Wilk test and not the Kolmogorov–Smirnov, as the latter is not powerful enough, especially when the group size is relatively small, or alternatively, plots such as Q–Q and P–P plots.13 In cases where the sample size is very small (n < 10 per group), it is advised to evaluate the data distribution visually using histograms, Q–Q plots, P–P plots or other graphical techniques. Even in situations where traditional statistical tests might not have enough power, these visual evaluations can provide valuable insights. Finally, we strongly advise against data transformation and normalisation due to issues related to back-transformation which can lead to interpretational problems.14
  • 5. Data should be presented properly according to their distribution. For normally distributed data, the mean and standard deviation (SD) or standard error of the mean (SEM) are commonly used as measures of central tendency and spread, respectively. When dealing with skewed data, on the other hand, the median and interquartile range (IQR) can be used as robust measures of central tendency and spread, respectively.
  • 6. Authors should always mention the post-hoc tests used following ANOVA, Kruskal–Wallis, Friedman test, etc. When using ANOVA, authors should be aware that when the assumption of equal variances is violated, ANOVA may lead to incorrect results, inflating the Type I error rate. In such cases, Welch ANOVA is a suitable alternative, as it does not assume equal variances and is robust to violations of this assumption.15
  • 7. Outliers are data points that differ significantly from the majority of the data and, if not properly handled, can have a significant impact on statistical analyses and results. Outliers should not be excluded from the analysis without a valid justification. This approach may result in biased estimates, misleading conclusions, and loss of valuable information. Outliers might, often, be actual extreme values or unique observations that are crucial to comprehending the underlying phenomenon.
  • 8. Authors should provide the accurate p values together with the statistical test used ie “(unpaired t-test, p = 0.03)” and not just “(p<0.05)”.

    • Statistical analysis is the foundation of both clinical and experimental medical research. To ensure the credibility and replicability of their findings, authors must take a rigorous and transparent approach to data analysis and presentation. Reviewers must also understand statistical principles in order to evaluate the validity of submitted manuscripts. While the process may appear daunting, we hope that this information has helped to simplify some important aspects of statistical analysis. Remember that statistics do not constitute a necessary evil, but rather a necessary tool in our scientific endeavour. Collaboration between authors and statisticians is essential for the advancement of medical research and we strongly recommend that authors seek professional statistical advice when this is necessary.

    Disclosure

    The authors have no conflicts of interest in this work.

    References

    1. Fieberg JR, Vitense K, Johnson DH. Resampling-based methods for biologists. PeerJ. 2020;8:e9089. doi:10.7717/peerj.9089

    2. Dwivedi AK, Mallawaarachchi I, Alvarado LA. Analysis of small sample size studies using nonparametric bootstrap test with pooled resampling method. Stat Med. 2017;36(14):2187–2205. doi:10.1002/sim.7263

    3. Neuhauser M, Jockel KH. A bootstrap test for the analysis of microarray experiments with a very small number of replications. Appl Bioinformatics. 2006;5(3):173–179. doi:10.2165/00822942-200605030-00005

    4. Gupta KK, Attri JP, Singh A, Kaur H, Kaur G. Basic concepts for sample size calculation: critical step for any clinical trials! Saudi J Anaesth. 2016;10(3):328–331. doi:10.4103/1658-354X.174918

    5. Schulz KF, Grimes DA. Sample size calculations in randomised trials: mandatory and mystical. Lancet. 2005;365(9467):1348–1353. doi:10.1016/S0140-6736(05)61034-3

    6. Festing MF. Design and statistical methods in studies using animal models of development. ILAR J. 2006;47(1):5–14. doi:10.1093/ilar.47.1.5

    7. Arifin WN, Zahiruddin WM. Sample size calculation in animal studies using resource equation approach. Malays J Med Sci. 2017;24(5):101–105. doi:10.21315/mjms2017.24.5.11

    8. Mancl LA, Leroux BG, DeRouen TA. Between-subject and within-subject statistical information in dental research. J Dent Res. 2000;79(10):1778–1781. doi:10.1177/00220345000790100801

    9. Murdoch I. People and eyes: statistics in ophthalmology. Community Eye Health. 1998;11(27):43.

    10. Cheng CY, Liu JH, Chiang SC, Chen SJ, Hsu WM. Statistics in ophthalmic research: two eyes, one eye or the mean? Zhonghua Yi Xue Za Zhi. 2000;63(12):885–892.

    11. Nikinmaa M, Celander M, Tjeerdema R. Replication in aquatic biology: the result is often pseudoreplication. Aquat Toxicol. 2012;116–117:iii–iv.

    12. Emmerich C. Accurate design of in vitro experiments – why does it matter? 2019. Available from: https://paasp.net/accurate-design-of-in-vitro-experiments-why-does-it-matter/. Accessed June 30, 2023.

    13. Ghasemi A, Zahediasl S. Normality tests for statistical analysis: a guide for non-statisticians. Int J Endocrinol Metab. 2012;10(2):486–489. doi:10.5812/ijem.3505

    14. Lee DK. Data transformation: a focus on the interpretation. Korean J Anesthesiol. 2020;73(6):503–508. doi:10.4097/kja.20137

    15. Jan SL, Shieh G. Sample size determinations for Welch’s test in one-way heteroscedastic ANOVA. Br J Math Stat Psychol. 2014;67(1):72–93. doi:10.1111/bmsp.12006

    Creative Commons License © 2023 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License. By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.

    Download Article [PDF]