Back to Journals » Clinical Epidemiology » Volume 6
Empirical comparison of four baseline covariate adjustment methods in analysis of continuous outcomes in randomized controlled trials
Authors Zhang S, Paul J, Nantha-Aree M, Buckley N, Shahzad U, Cheng J, DeBeer J, Winemaker M, Wismer D, Punthakee D, Avram V, Thabane L
Received 25 October 2013
Accepted for publication 13 January 2014
Published 14 July 2014 Volume 2014:6 Pages 227—235
DOI https://doi.org/10.2147/CLEP.S56554
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Shiyuan Zhang,1 James Paul,2 Manyat Nantha-Aree,2 Norman Buckley,2 Uswa Shahzad,2 Ji Cheng,2 Justin DeBeer,5 Mitchell Winemaker,5 David Wismer,5 Dinshaw Punthakee,5 Victoria Avram,5 Lehana Thabane1–4
1Department of Clinical Epidemiology and Biostatistics, 2Department of Anesthesia, McMaster University, Hamilton, ON, Canada; 3Biostatistics Unit/Centre for Evaluation of Medicines, St Joseph's Healthcare - Hamilton, Hamilton, ON, Canada; 4Population Health Research Institute, Hamilton Health Science/McMaster University, 5Department of Surgery, Division of Orthopaedics, McMaster University, Hamilton, ON, Canada
Background: Although seemingly straightforward, the statistical comparison of a continuous variable in a randomized controlled trial that has both a pre- and posttreatment score presents an interesting challenge for trialists. We present here empirical application of four statistical methods (posttreatment scores with analysis of variance, analysis of covariance, change in scores, and percent change in scores), using data from a randomized controlled trial of postoperative pain in patients following total joint arthroplasty (the Morphine COnsumption in Joint Replacement Patients, With and Without GaBapentin Treatment, a RandomIzed ControlLEd Study [MOBILE] trials).
Methods: Analysis of covariance (ANCOVA) was used to adjust for baseline measures and to provide an unbiased estimate of the mean group difference of the 1-year postoperative knee flexion scores in knee arthroplasty patients. Robustness tests were done by comparing ANCOVA with three comparative methods: the posttreatment scores, change in scores, and percentage change from baseline.
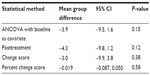
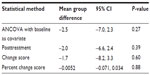
Results: All four methods showed similar direction of effect; however, ANCOVA (-3.9; 95% confidence interval [CI]: -9.5, 1.6; P=0.15) and the posttreatment score (-4.3; 95% CI: -9.8, 1.2; P=0.12) method provided the highest precision of estimate compared with the change score (-3.0; 95% CI: -9.9, 3.8; P=0.38) and percent change (–0.019; 95% CI: -0.087, 0.050; P=0.58).
Conclusion: ANCOVA, through both simulation and empirical studies, provides the best statistical estimation for analyzing continuous outcomes requiring covariate adjustment. Our empirical findings support the use of ANCOVA as an optimal method in both design and analysis of trials with a continuous primary outcome.
Keywords: ANOVA, ANCOVA, change score, knee arthroplasty
A Letter to the Editor has been received and published for this article.
Introduction
Continuous outcomes are one of the most common types of outcomes used in clinical trials. They are easy to interpret for statistician and clinicians alike. For instance blood pressure, glucose level, or forced expiratory volume in one second (FEV1) are continuous in nature and understandable without requiring much manipulation to the data.
In a number of research fields, such as psychology, education, pain, and quality of life, a common randomized controlled trial (RCT) design involves the measurement of the primary outcome in the comparator groups at two time points. The measurement occurs before (commonly known as baseline or covariate values) and after the treatment.1 This type of baseline-controlled design can be a very statistically powerful design to evaluate causal factors since adjustment of unbalanced covariates can be properly done in order to isolate the factors at work.2−5 This design is often of great use to evaluators because it can control for all of the major threats to internal validity, such as maturation, selection, and instrumentation.6
Clinical problem: Inconsistency in choosing the method for baseline adjustment
Although seemingly straightforward, the statistical comparison of a continuous variable in an RCT that has both a pre- and posttreatment score presents an interesting challenge for clinician and statistician. The statistical properties of baseline adjustment methods are complex and often poorly understood, resulting in confusion about the choice of the most appropriate statistical strategy.7 Assman et al analyzed a sample of 50 trials from four top medical journals, British Medical Journal, Journal of the American Medical Association, The Lancet, and New England Journal of Medicine,8 and reported the use of seven different covariate-adjustment methods. The lack of consistency in the literature on pre−post design further contributes to the difficulty of establishing a standard statistical method. The inconsistency often relates to whether covariate adjustment is appropriate for the analysis and the selection of baseline factors for the adjustment.
Critical appraisal of four adjustment methods
There are a number of baseline adjustment methods commonly used in clinical trials, for reasons of ease of interpretation, ease of analysis, convenience, and historical factors. Statisticians have evaluated the methods to determine the most appropriate estimate of size, precision, and P-value for the treatment difference.9,10 The four methods examined are: posttreatment comparison (no baseline adjustment), analysis of covariance (ANCOVA), change score, and percent change score.2–4 Specifically, for each method, a brief description of the method and the advantages and disadvantages are described.
Posttreatment comparison
In this method, analysis is done on the outcome of interest, with no covariate adjustment, testing one or more continuous variables that predict the outcome of interest. There are a number of advantages of comparing simply the unadjusted outcome, including minimal influence by a secondary outcome, straightforward interpretation of the result, and the short time required for the analysis − this is the least time consuming method. Moreover, for most clinical trials, analyses adjusting for baseline covariates yield similar results compared with the simpler unadjusted treatment comparisons.8
Another rationale for using the posttreatment score method with a simple analysis of variance (ANOVA) or Student’s t-test is that in practice, randomization allows for a balanced baseline measure in both treatment groups, and thus, covariate adjustment is deemed unnecessary. This assumption of balanced baseline variable can, however, be violated even in the perfectly designed RCT, and the effect is especially magnified in trials with a small sample size.11 In fact, results from simulation studies have shown that when the baseline is adjusted, the analysis of posttreatment score can be different.12
Analysis of covariance
In recent published literature, the use of ANCOVA as the statistical method of choice for the analysis of intervention effect and adjustment for baseline variables has been advocated.13−18 ANCOVA uses the baseline result as a covariate in the analysis. In addition to the grouping factor and the outcome of the posttreatment score, an additional covariate term is introduced that allows for a statistical adjustment based on the baseline score.
There are three reasons for using ANCOVA in the analysis of continuous outcomes − efficiency, precision, and power. In RCTs, when the treatment and placebo group have the same expected mean baseline values, both the posttreatment score method and the ANCOVA model will provide an unbiased estimate of the true treatment effect.11 However, ANCOVA provides the advantage of greater efficiency and better statistical power, even under unbiased conditions and with controlled α-levels. Even in the presence of measurement error or other within-patient variations, the ANCOVA approach based on the observed data provides an unbiased estimate, and better precision and a more powerful test than the ANOVA.
The main disadvantage of ANCOVA is the underlying assumption of no difference across groups or treatment arms in terms of the covariate used in the analysis and the homogeneity of regression slopes. In RCTs where the covariates differ across the treatment arms, the overall regression model will provide inaccurate estimates and therefore use of ANCOVA should be avoided.
Change score between posttreatment and baseline
Clinical trials with quality of life as an outcome often calculate it by subtracting the baseline value from the follow-up or posttreatment value. This is often referred to as a change score or sometimes (optimistically) the gain score, and it directly represents the change that is reported or measured before and after the treatment. Using change score may provide an advantage over ANCOVA because it is not necessary to assume that baseline variables are measured without error.13 Even in ANCOVA models that attempt to adjust for measurement error, the estimate of treatment effect remains biased.19 However, one issue with the change score method is that the “regression to the mean” effect could be substantially different between the comparator groups.
Percent change score between posttreatment score and baseline
A modification of the change score that preserves some of the information of the baseline result is calculation of the change score as a percentage. Percent change score is calculated by normalizing the change score using the baseline data. It can be considered an improvement to represent the change pre- and posttreatment in a normalized fashion, which increases comparability across subjects. However, one major concern is that normalizing the data may alter the distribution of the data and may introduce additional complexity to the analysis.
Study objective
In this study, four methods of baseline adjustment were used to demonstrate empirically whether the ANCOVA is statistically efficient compared with statistical analysis by posttreatment score, change score, or percent change score. To compare methods, previously reported outcome data20 (flexion range of motion) was analyzed using ANCOVA and the other three methods outlined above. The robustness of the latter three methods was evaluated by qualitatively comparing the direction and magnitude of effect, the precision of the estimate, and the ease of interpretation of the results. The study also sought to identify the best approach to handle missing data in clinical trials. This was done through the use of multiple imputation (MI), where a sensitivity analysis was done by conducting a complete-case analysis (CCA).21
Methods
Current literature review and summary
A search of published literature on baseline adjustment methods was conducted to summarize the available information on the use of the statistical methods and their impact on the results of studies. Three different designs of studies were included in the search; descriptive, empirical, and simulation studies. Descriptive studies were defined, in this study, as “systematic reviews or compilation studies where a cohort of studies is summarized to address the current knowledge on the topic area.” Empirical studies were defined as “studies where data from another previously published study is subjected to reanalyses using different statistical methods to compare and contrast the methods and results.” Simulation studies were “studies where statistical methods are compared in terms of statistical power and other parameters, using statistical and mathematical simulation.” Studies of these designs were compiled and results were summarized in terms of the impact of the method on the results and the author’s assessment of the choice of the most appropriate statistical method.
We also sought to conduct an empirical study to examine the four baseline covariate adjustment methods. Empirical data from The Morphine COnsumption in Joint Replacement Patients, With and Without GaBapentin Treatment, a RandomIzed ControlLEd Study (MOBILE trial)20 was used to demonstrate the performance of different baseline adjustment methods and their effect on the statistical comparison. The statistical properties of covariate adjustments were examined in terms of several aims, including: 1) the direction of the treatment difference; 2) the magnitude of the treatment difference; and 3) the precision of the treatment difference.9,10
Description of MOBILE trial: total knee arthroplasty
In a single-center, blinded, randomized, placebo-controlled study, 102 patients were randomized to receive either gabapentin or placebo, in addition to standard of care, 2 hours before undergoing total knee arthroplasty.20 Morphine consumption at 72 hours was the primary end point of the trial. Secondary outcomes included knee flexion score, pain score on a visual analog scale, and side effects. In the trial, the statistical analysis was done without the adjustment of baseline covariates, and a posttreatment score comparison was reported for the knee flexion variable.
For patients undergoing total knee arthroplasty, the variables used for analysis were flexion range of motion preoperatively and at 1 year after the procedure. Other than patient identification, group assignment, and the two flexion range-of-motion values, the baseline and postoperative variables included in the data collection process were: sex, weight, height, American Society of Anesthesiologists (ASA) physical status classification system, systolic blood pressure, diastolic blood pressure, pain at rest at the four different time points, pain with passive movement at the time points, pain with weight-bearing at the same four different time points. The percentage of missing data for these variables ranged from 0.0% (five variables) to 15.9% (only pain with weight-bearing at time 3). To follow an intention-to-treat analysis, where all patients randomized were included in the analysis, these variables were included in the MI strategy. In the MI process, all of these variables were imputed in a coherent process, using the Markov chain Monte Carlo (MCMC) method.22 Five iterations of the MI process were used for the analyses of the knee flexion range-of-motion data, and MIANALYZE, a procedure in SAS (SAS Institute, Inc., Cary, NC, USA), was used to combine the estimates from each of the five iterations.22
Analysis of postoperative knee flexion range of motion, adjusting for baseline
Four baseline adjustment methods were used to obtain a statistical comparison of the control against the active group. ANCOVA was used and the pretreatment knee flexion range-of-motion score was used as a covariate to determine the treatment effect after data imputation by MI. The treatment effect estimate, 95% confidence interval (CI), and P-value were summarized. All statistical tests were performed using SAS (SAS 9.2 (32) English).
Sensitivity analysis
Two robustness tests were conducted to evaluate sensitivity. Specifically, a robustness test was done to determine the sensitivity of the results to the method of analysis, and another test was done to determine the sensitivity to missing data.
Robustness of posttreatment, change, and percent change analysis
Three other methods were used as comparators with the ANCOVA analysis to determine the sensitivity of the results to the choice of baseline adjustment method. The other three baseline adjustment methods were: comparing the posttreatment scores only, with no baseline adjustment; comparing the change score by subtracting the baseline from the posttreatment score; and comparing the percent change score obtained from normalizing the change score by dividing the change score by the pretreatment score (Figure 1). For the purposes of this robustness test, data were imputed by MI. The robustness of each of the three methods was determined based on the following factors: direction and magnitude of effect, and the precision of the estimate. To further illustrate the robustness of the results obtained from ANCOVA and the potential difference between ANCOVA and the other three methods, a forest plot of the 95% CI of each of the four analyses was used to provide a visual comparison.
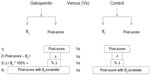  | Figure 1 The schematic depiction of the four baseline adjustment methods. |
Robustness of complete-case analysis
To decide whether the results were affected qualitatively by the implementation of MI, the results of the CCA for each of the baseline adjustment methods was used as the comparator. The robustness test was done by comparing the two types of data handling methods, based on direction and magnitude of effect, and the precision of estimate. To further illustrate the difference between the two methods of handling missing data, a forest plot of the 95% CI of each of the eight analyses was used to provide a visual comparison.
Results
Highlights of the literature on use of baseline adjustment methods
The use of these four different methods has been documented in the literature numerous times (see Table 1), through both simulation studies and studies using empirically derived data. For instance, Tu et al used empirical results from periodontal research to demonstrate that different statistical methods have a substantial impact on study power.15 In this study, it was demonstrated that with substantial variability in the correlation between the baseline and posttreatment score, ANCOVA should be used in preference to change score or percentage change score, as the appropriate method that is able to adequately reduce the type II error rates. Other examples of studies are summarized in Table 1. In short, most empirical studies reported that ANCOVA is often the most appropriate statistical method to adjust for baseline covariates when analyzing randomized studies of continuous outcome.7,8,14 Similarly, theoretical and simulation studies have shown that ANCOVA had the highest statistical power and was the method of choice.13,23,24 However, in nonrandomized studies, ANCOVA may yield biased results and the change score method should be used as the method of analysis.
Lastly, descriptive studies that summarized analyses from a large number of individual studies have shown that the selection of the method of baseline adjustment caused confusion for researchers. Specifically, there was no single method that was consistently used and often times, no justification was provided for the choice of the method used.7,8
Analysis of treatment effect
In the MOBILE study, the mean group difference, with the gabapentin treatment as the treatment group was −5.5. This indicated that the knee flexion range of motion of the patients in the active treatment group was 5.5 less, on average, than that of patients in the control group. The lower and upper 95% CIs were −11 and 0.25, P-value was 0.068, and the difference between the two treatment arms was not statistically significant.
Sensitivity analysis
Sensitivity to method of analysis/baseline adjustment
The primary analysis for the range-of-motion data was conducted using ANCOVA with MI for handling missing data (Figure 2 and Tables 2 and 3). The first set of sensitivity analyses compared ANCOVA with the other three methods of adjusting for baseline data and conducting statistical comparison. The three methods all had similar direction of effect, where the group mean of flexion range of motion in the control group was higher than that of the active treatment group. Moreover, the magnitude of the result of each of the three methods was similar to that obtained from the ANCOVA method, ranging from 3.9 to 4.3 (compared with 5.5 obtained using ANCOVA). The precision of the results was lower with the change score and percent change score methods, each of which had a much larger CI and P-value.
The group effect obtained using the posttreatment scores method without a baseline adjustment had the most similar results compared with ANCOVA. Along with having the same direction and almost identical magnitude of effect, the 95% CI was narrower and had a correspondingly smaller P-value. Overall, the results of the posttreatment scores remained robust, and the findings were consistent. The results obtained from the change score and percent change score methods had larger deviations compared with the primary analysis. Although they had the same direction of effect, the magnitude of effect was less, and a wider 95% CI was obtained. Of the three comparator methods, posttreatment offered the most robust method of analysis compared with ANCOVA, and the change score and percent change score methods offered the least favorable method in terms of precision and magnitude of effect (Figure 2).
Sensitivity to missing data
The second set of sensitivity analyses were done for different methods of handling missing data for flexion range of motion (Figure 2 and Tables 2 and 3). For the knee range-of-motion score, 4% and 25% of the data were missing at baseline and at the posttreatment follow-up, respectively. The primary analysis for the range of motion used ANCOVA, with MI for handling missing data. When CCA was used, the mean group difference was −2.5 (95% CI: −7.0, 2.3; P=0.27). Without any method of handling the missing data, the analysis of ANCOVA remained robust. The results maintained the direction of effect, where both estimates suggested a slight favoring of the control group. Moreover, the magnitude of the effect was also similar, where the point estimate was different by only 1.4. The level of precision was similar between MI and CCA. The P-value of the CCA was larger, due to the decrease in the precision of the analysis caused by having a low number of cases available for analysis.
In comparing results between the two methods of handling missing data among the other three methods of outcome analysis (posttreatment, change score, and percent change), the same trends were observed (data not shown). All results had the same direction of effect, with a slightly smaller magnitude of effect, smaller confidence interval, and larger P-values. The details of these results are summarized in Tables 2 and 3.
Discussion
Key findings
The present study used empirical data from total knee arthroplasty patients from the MOBILE trial and reanalyzed it to determine the impact on treatment effect (postoperative flexion range-of-motion score) of using different statistical methods of dealing with adjustment of baseline differences. With the method of ANCOVA while using MI to handle missing data, the results suggest the difference in knee flexion between the gabapentin and control group was not statistically significant. Our empirical findings support the use of ANCOVA as an optimal method in both the design and analysis of trials with a continuous primary outcome.
Through sensitivity analysis of both the method of analysis and the method of handling missing data, it is reported that all methods remained robust, and the overall findings were consistent. It should be noted, however, that while the results are similar, there are distinguishable features. For instance, it is reported that using the posttreatment score alone as the variable for statistical comparison yielded the most similar results to those from the ANCOVA method. In a simulation study published by Vickers and Altman,17 the statistical power of these four baseline adjustment methods was compared at different baseline to outcome score correlations. The results of the empirical study reported here corroborate the simulation study, where at low correlation levels, the ANCOVA and posttreatment score maintained statistical power at around 70%. Moreover, for the change score and percent change score, the statistical power decreased dramatically with the decrease of the baseline to outcome score correlation, where at a correlation of 0.2, the statistical power fell to around 50%. In this study there was no significant correlation between the baseline and postoperative range of motion; thus it would be interpreted as a near-zero correlation. Although the lowest correlation used in the simulation study was 0.2, it could be confidently extrapolated that for the analysis of data with no correlation, the ANCOVA and posttreatment methods will have the highest statistical power. Furthermore, change score and percent change score will have even lower statistical power than at the 0.2 correlation level. However, these conclusions were made at a qualitative level, and no power calculation was done to determine the exact power of the various methods.
There are a number of methods commonly used for handling missing data. For a long time, the preferred method of handling missing data was single imputation, by either imputing with the grand mean, or with last observation carried forward. There is increasing evidence and support for MI to be used as the primary method of handling missing data.21 In the present study, the sensitivity analysis for the methods of handling missing data suggests that the conclusion drawn was unaffected by the use of either CCA or MI. Moreover, in the MOBILE trial, and in this study, we sought to follow an intention-to-treat principle, where all patients randomized were analyzed. The methods utilized for statistical comparison were quite robust even when missing data was ignored.
Key limitations
The brief literature review presented in Table 1 was not conducted as a systematic literature search. The summary provided attempted to highlight recent literature on the topic of covariate baseline adjustment methods used in simulation or empirical studies. It provided information that highlights the advantages and disadvantages of these various methodologies. The results and conclusions drawn from these studies were not used to make inferences on the superiority of one method over the others. Nonetheless, the information gathered from this study helps to distill and assimilate large amounts of information in order to provide a quick overview of some of the research conducted in this topic area.
One of the main limitations of the empirical analysis portion of the study is the nature of the variable used in this study, which was the flexion range of motion. In the MOBILE trial, the sample size estimation was based on the primary outcome, which was the cumulative morphine consumption at 72 hours postsurgery. Therefore, with a sample size of 101, there may have been a lack of power to detect a difference between the two groups even if a true difference exists. As such, the results should be interpreted with caution due to the potential lack of sufficient power.
In this study, missing data were handled by using MI with five iterations. Although MI has been recognized as the most appropriate method for imputing missing data, it assumes that the “missingness” is either missing completely at random (MCAR) or at least missing at random (MAR).21 Currently, no methods are available for analysis of data that are “missing not at random.” However, testing for the type of missing data mechanism is difficult, especially when there is a lack of auxiliary information, such as the demographic and social characteristics of the participants. For the purposes of this study, the missingness was assumed to be MAR since only a small portion of the data are missing. Moreover, the robustness of the CCA further suggests that there was not a substantial amount of missing data.
The comparison of this study, using empirical data, with previous simulation studies suggests similarity in the findings. However, interpretation of the results should be understood as obtained from an empirical study, where the characteristics of the data used may influence the results generated. This is to say that although change score and percent change have been suggested as less statistically efficient methods of adjusting for baseline, when the baseline data is highly correlated with the posttreatment score, change and percent change scores may be a valid and easily interpreted methods to be used. Regardless, since ANCOVA has been shown, in a variety of studies,7,9,13,15,18,24,25,27,28 as the most statistically efficient method to analyze continuous outcomes with a baseline variable, it is suggested that the adoption of other methods of handling baseline data be used with caution.
Conclusion
In this study, we compared the most commonly used methods for adjusting the baseline data of a continuous outcome in an RCT, using an existing empirically derived dataset. The study results suggest that ANCOVA is a statistically efficient method of analyzing data of this nature and also, that the use of change and percent change scores should be employed with caution since the statistical power of these methods is highly dependent on the correlation between the baseline and the outcome. Although the findings of this study can be limited to only trials with no correlation between the adjustment variables, it should be noted that the study does contribute to the growing body of evidence on this subject, where ANCOVA has been shown as the method with the most advantages. A number of future studies should be conducted to strengthen the interpretation of this study. Simulation studies with a correlation of baseline and outcome lower than 0.2 can contribute to the evaluation of the conclusion of this study. Moreover, empirical data that were intended as the primary outcome of the study should be used in order to ensure the validity of this analysis.
Future studies may look at logistic regression and how the method of covariate adjustment affects the results.26 For instance, it is known that when the covariate included in the trial is that of a binary or survival nature, the adjustment methodology and implications are completely different. The omission of a balanced covariate has dramatic effects on the estimate of treatment effect, and this effect is magnified when a highly prognostic covariate is included in the analysis. Investigating some of these scenarios and developing a complete empirical study based on the various baseline adjustment methods set out in this study would be of great interest.9
Author contributions
LT, JP, MNA, and SZ conceived the idea and designed the study; SZ, LT, JP, MNA, NB, US, JC, JD, MW, DW, DP and VA contributed to analysis and interpretation of data. SZ, LT, JP, MNA, NB, US, JC, JD, MW, DW, DP and VA contributed to the acquisition of data. SZ, LT drafted the article. SZ, JP, MNA, NB, US, JC, JD, MW, DW, DP, VA, LT contributed to writing and critically revising the manuscript. All authors read and approved the final manuscript.
Disclosure
The authors report no conflicts of interest in this work.
References
Beach ML, Meier P. Choosing covariates in the analysis of clinical trials. Control Clin Trials. 1989;10(Suppl 4):161S−175S. | |
Bonate PL. Analysis of Pretest-Posttest Designs. Boca Raton, FL: Chapman and Hall/CRC; 2000. | |
Dimitrov DM, Rumrill PD. Pretest-posttest designs and measurement of change. Work. 2003;20(2):159–165. | |
Schafer WD. Analysis of pretest-posttest designs. Measurement and Evaluation in Counseling and Development. 1992;25(1):2−4. | |
Rossi PH, Lipsey MW, Freeman HE. Evaluation: A Systematic Approach. 7th ed. Thousand Oaks, CA: Sage Publications, Inc.; 2004. | |
Campbell DT, Stanley JC, Gage NL. Experimental and Quasi-Experimental Designs for Research. Boston, MA: Houghton Mifflin Company; 1963. | |
Pocock SJ, Assmann SE, Enos LE, Kasten LE. Subgroup analysis, covariate adjustment and baseline comparisons in clinical trial reporting: current practice and problems. Stat Med. 2002;21(19):2917–2930. | |
Assmann SF, Pocock SJ, Enos LE, Kasten LE. Subgroup analysis and other (mis)uses of baseline data in clinical trials. Lancet. 2000; 355(9209):1064–1069. | |
Raab GM, Day S, Sales J. How to select covariates to include in the analysis of a clinical trial. Control Clin Trials. 2000;21(4):330–342. | |
Senn SJ. Covariate imbalance and random allocation in clinical trials. Stat Med. 1989;8(4):467–475. | |
Wei L, Zhang J. Analysis of data with imbalance in the baseline outcome variable for randomized clinical trials. Drug Information Journal. 2001;35(4):1201−1214. | |
Overall JE, Magee KN. Directional baseline differences and type I error probabilities in randomized clinical trials. J Biopharm Stat. 1992;2(2):189–203. | |
Oakes JM, Feldman HA. Statistical power for nonequivalent pretest-posttest designs. The impact of change-score versus ANCOVA models. Eval Rev. 2001;25(1):3–28. | |
Tu YK, Baelum V, Gilthorpe MS. A structural equation modelling approach to the analysis of change. Eur J Oral Sci. 2008;116(4):291–296. | |
Tu YK, Blance A, Clerehugh V, Gilthorpe MS. Statistical power for analyses of changes in randomized controlled trials. J Dent Res. 2005;84(3):283–287. | |
Winkens B, van Breukelen GJ, Schouten HJ, Berger MP. Randomized clinical trials with a pre- and a post-treatment measurement: repeated measures versus ANCOVA models. Contemp Clin Trials. 2007;28(6):713–719. | |
Vickers AJ, Altman DG. Statistics notes: Analysing controlled trials with baseline and follow up measurements. BMJ. 2001;323(7321):1123–1124. | |
Van Breukelen GJ. ANCOVA versus change from baseline: more power in randomized studies, more bias in nonrandomized studies [corrected]. J Clin Epidemiol. 2006;59(9):920–925. | |
Chan SF, Macaskill P, Irwig L, Walter SD. Adjustment for baseline measurement error in randomized controlled trials induces bias. Control Clin Trials. 2004;25(4):408–416. | |
Paul JE, Nantha-Aree M, Buckley N, et al. Gabapentin does not improve multimodal analgesia outcomes for total knee arthroplasty: a randomized controlled trial. Can J Anaesth. 2013;60(5):423–431. | |
Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychol Methods. 2002;7(2):147–177. | |
SAS Institute Inc. SAS® 9.1.3 Language Reference: Concepts, Third Edition. Cary, NC: SAS Institute Inc; 2005. Available from: http://support.sas.com/documentation/onlinedoc/91pdf/sasdoc_913/base_lrconcept_9196.pdf. Accessed March 26, 2014. | |
Liu GF, Lu K, Mogg R, Mallick M, Mehrotra DV. Should baseline be a covariate or dependent variable in analyses of change from baseline in clinical trials? Stat Med. 2009;28(20):2509–2530. | |
Wright DB. Comparing groups in a before-after design: when t test and ANCOVA produce different results. Br J Educ Psychol. 2006; 76(Pt 3):663–675. | |
Tariot PN, Solomon PR, Morris JC, Kershaw P, Lilienfeld S, Ding C. A 5-month, randomized, placebo-controlled trial of galantamine in AD. The Galantamine USA-10 Study Group. Neurology. 2000;54(12):2269–2276. | |
Robinson LD, Jewell NP. Some surprising results about covariate adjustment in logistic regression models. International Statistical Review/Revue Internationale de Statistique. 1991;59(2):227−240. | |
Vickers AJ. Statistical reanalysis of four recent randomized trials of acupuncture for pain using analysis of covariance. Clin J Pain. 2004;20(5):319–323. | |
Cribbie R, Jamieson J. Decreases in posttest variance and the measurement of change. Methods of Psychological Research Online. 2004;9(1):37−55. |
 © 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.