Back to Journals » Risk Management and Healthcare Policy » Volume 13
Association Between Supplemental Private Health Insurance and Burden of Out-of-Pocket Healthcare Expenditure in China: A Novel Approach to Estimate Two-Part Model with Random Effects Using Panel Data
Received 13 July 2019
Accepted for publication 21 January 2020
Published 14 April 2020 Volume 2020:13 Pages 323—334
DOI https://doi.org/10.2147/RMHP.S223045
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Kent Rondeau
Yawen Jiang,1 Weiyi Ni2
1School of Public Health (Shenzhen), Sun Yat-sen University, Guangzhou, Guangdong, People’s Republic of China; 2Department of Pharmaceutical and Health Economics, University of Southern California, Los Angeles, CA 90089-3333, USA
Correspondence: Yawen Jiang
School of Public Health (Shenzhen), Sun Yat-sen University, Room 215, Mingde Garden #6, 132 East Outer Ring Road, Pan-Yu District, Guangzhou, Guangdong, People’s Republic of China
Tel +1 213-320-1361
Email [email protected]
Introduction: Private health insurance (PHI) is an important supplement to the basic health insurance schemes in the Chinese healthcare system. However, there is an absence of evidence on whether the strategy of engaging PHI to reduce burden is effective in China. As such, we aimed to investigate the association between supplemental PHI and the out-of-pocket (OOP) burden of household healthcare expenditure in China.
Methods: We conducted a panel data analysis using data from three waves of China Health and Retirement Longitudinal Study (CHARLS). Specifically, a two-part model (TPM) with a first-stage probit and second-stage generalized linear model (GLM) framework was used to analyze the data. To account for individual-level random effects in both stages and their correlation in the TPM analysis, we proposed a generalized structural equation modeling (GSEM) approach to implement the estimation. The proposed approach allowed us to simultaneously analyze the association of PHI with the probability of having any healthcare and the OOP burden conditional on having any healthcare expenditure.
Results: Using the GSEM estimates, we found that supplemental PHI was significantly associated with a higher probability (4.29 percentage points) of having any OOP healthcare expenditure but a lower OOP burden conditional on having any expenditure (− 2.37 percentage points). Overall, supplemental PHI was insignificantly associated with a lower OOP burden (− 1.05 percentage points).
Discussion: Our findings suggested that supplemental PHI in China may be able to effectively improve access to healthcare while keeping the OOP healthcare expenditure burden flat. Also, GSEM is a feasible method to estimate random-effect TPMs.
Keywords: private, health insurance, China, out-of-pocket, burden
Introduction
Although the basic public health insurance coverage in China increased from 50% to a near-universal rate of 95% during 2005–2011,1,2 the high out-of-pocket (OOP) rate associated with public health insurance that ranges from 40% to 70% remains a financial challenge to patients with severe illness.1,3,4 In the meantime, the government medical insurance fund is running on a tight budget in the context of a continuously aging population.5,6 As an attempt to avoid overloading itself, the government has proposed a “multi-level health insurance system” in which public health insurance is supposed to secure basic healthcare need and private health insurance (PHI) is an important supplement that mainly focuses on high-cost care.7 However, the coverage rate of supplemental PHI in China has barely reached 4%.1,3
Naturally, the scheme of supplementing public health insurance with PHI only works if PHI can effectively improve access to costly service, reducing the OOP burden or both. However, empirical evidence on the association of the current supplemental PHI in China with the burden of out-of-pocket (OOP) healthcare expenditure is still absent in the literature. In addition, such association cannot be inferred using evidence from other regions because the regulation of the PHI market and the PHI plans in China are not comparable. For example, discrimination based on pre-existing conditions is not prohibited in the Chinese PHI market. In addition, PHI policies usually do not provide real-time reimbursement based on actual service costs. Instead, they pay a lump sum for a narrow set of conditions if the diagnosis and its eligibility for reimbursement is confirmed.4,8 Once the one-time benefit is claimed, the renewal of enrollment becomes unlikely.4 Therefore, the enrollees who survive a health shock will possibly become exposed to potential future financial risk because of losing the supplemental PHI coverage.
These aspects of supplemental PHI in China raise several theoretical concerns that may undermine its financial protection effect. First, the absence of real-time reimbursement and the lack of a priori knowledge of the reimbursement eligibility of the services in need can make patients cautious about using services because there is a risk that a patient is not reimbursed subsequently. Second, the lump sum payment may reserve individual motivation to spend frugally because any remaining cash becomes the beneficiary’s wealth. Finally, the lack of commitment to continuous enrollment by the commercial insurers may disincentivize highly risk-averse individuals to claim the benefit if these individuals expect more costly medical occurrence in future.
Given these atypical properties of PHI in China, it is important to obtain China-specific empirical evidence on the association between PHI and the burden of OOP healthcare expenditure. Hence, the primary objective of the present study is to investigate whether PHI in China is associated with a lower burden of OOP healthcare expenditure. We define burden as the proportion of OOP healthcare expenditure out of total household consumption, which is the same metric that catastrophic healthcare expenditure is based on.9
In the current analysis, we used the China Health and Retirement Longitudinal Study (CHARLS) data. CHARLS is an aging survey of 45 years and older people and their spouses in China that used a multistage probability sampling to allow nationally representative estimates.3,10,11 The longitudinal surveys collected healthcare expenditure and total household consumption data from the respondents,12 which allowed us to exploit the panel structure of the data. However, at least two challenges can arise in the analysis of healthcare expenditure using panel data. The first challenge is that expenditure data is often semi-continuously distributed such that they have a large mass at zero, making single-index models inappropriate. In cross-sectional analyses, two-part models (TPMs) are often used to model two data-generation processes of which the first one predicts incurrence of expenditure and the second one predicts the intensity of expenditure conditional on having any.13 The second challenge is treating individual-specific effects in panel data. In econometrics, there are two general approaches to individual-specific effects in the analysis of panel data, namely fixed effects model and random effects model.14 To generate consistent estimates of coefficients, the two approaches make different assumptions about the correlation between unobserved individual-specific effects and included variables.15 Fixed effects models assume the unobserved individual-specific effects are time-invariant but correlated with the independent variable of interest, whereas random effects models assume the unobserved individual-specific effects can be time-varying yet uncorrelated with the independent variable of interest.16 With a few exceptions where conditional maximum likelihood estimators exist, fixed effect estimators including the first difference estimator, the within-group estimator and the dummy variable approach are biased in nonlinear models with small group sizes.14,17 Therefore, we focus the present analysis using random effects. In particular, we propose a new approach to implement TPMs with random effects, which is the secondary objective of the present study.
Review of Related Literature
Review of the Association Between Supplemental PHI and the Burden of OOP Healthcare Expenditure
To our knowledge, the association between supplemental PHI and the burden of OOP healthcare expenditure have not been specifically investigated in the literature in China or other countries. However, such association has been examined as part of studies on other topics in two US studies. Gross et al18 found that, among poor Medicare beneficiaries, those who had supplemental PHI had a significantly higher average OOP spending than those who did not have supplemental PHI. By contrast, Goldman and Zissimopoulos19 found that Medicare beneficiaries with supplemental PHI spent significantly less out of pocket than those without. Evidence on the association between having PHI and OOP spending in other regions has yet to be documented.
It should be noted that these studies did not investigate the proportion of total household consumption spent as OOP healthcare expenditure. The latter is arguably a better measure of household financial burden because the same amount of payment can cause drastically different consequences to different families.9,20
It is also worth reiterating that the effects of supplemental PHI heavily depend on the institutional settings. Especially, the Chinese PHI market is different from the PHI markets in the western countries for the reasons aforementioned. In addition, to what extent the basic health insurance addresses healthcare need can affect the behavior of supplemental PHI beneficiaries.21 Hence, the findings in the US do not necessarily bring implications to Chinese policymakers.
Review of TPMs and Random Effects in TPMs
In a cross-sectional setting without random effects, the TPM separately models
(1)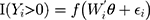
and
(2)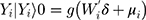
where (3) (4)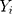 is the semi-continuous outcome variable, I() is an indicator of the condition in the parentheses, and
is the semi-continuous outcome variable, I() is an indicator of the condition in the parentheses, and 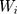 is a vector of independent variables. A TPM with a logistic or probit first part and a generalized linear model (GLM) second part is among the most popular specifications in health econometrics.22 However, other specifications such as ordinary least squares (OLS) and log-transformed models can be used in the second part depending on the distribution of explained variables.22 For healthcare expenditure data, natural logarithm is considered the appropriate link in the GLM.22 Advantages of using a GLM with a log link compared with OLS and the log-transformation of expenditure data, respectively, are that GLM allows non-negative yet skewed distribution and circumvents the retransformation bias issue of coefficient estimates to costs.13 The specification of the TPM model with a probit-GLM framework would take the following form if the data were cross-sectional and lacked random effects:
is a vector of independent variables. A TPM with a logistic or probit first part and a generalized linear model (GLM) second part is among the most popular specifications in health econometrics.22 However, other specifications such as ordinary least squares (OLS) and log-transformed models can be used in the second part depending on the distribution of explained variables.22 For healthcare expenditure data, natural logarithm is considered the appropriate link in the GLM.22 Advantages of using a GLM with a log link compared with OLS and the log-transformation of expenditure data, respectively, are that GLM allows non-negative yet skewed distribution and circumvents the retransformation bias issue of coefficient estimates to costs.13 The specification of the TPM model with a probit-GLM framework would take the following form if the data were cross-sectional and lacked random effects:
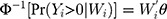
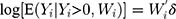
where (5)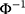 is the probit link function. Combining the two equations, we have
is the probit link function. Combining the two equations, we have
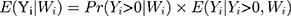
The coefficients in TPMs do not represent the magnitude of effects in the original scale of the dependent variable and are therefore not necessarily of interest to researchers and policymakers. The marginal effect (incremental effect for dichotomous variable, Appendix 1; for simplicity, both are referred to as marginal effects in the rest of the paper), which denotes the change in (6)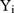 in response to a unit change in the jth independent variable,
in response to a unit change in the jth independent variable, 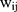 , is more interpretable than coefficients. With equations (3) and (4), the marginal effect is
, is more interpretable than coefficients. With equations (3) and (4), the marginal effect is 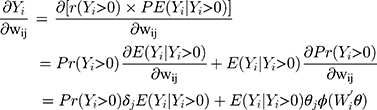
where 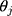 and
and 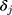 are the coefficients of
are the coefficients of 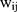 in the first and second equations of the model, respectively. Not only the total marginal effects need to take into consideration the effects of
in the first and second equations of the model, respectively. Not only the total marginal effects need to take into consideration the effects of 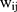 in both the first part and the second part, but also the standard error estimation of the total marginal effects should incorporate the uncertainty in both equations. The closed form solution of the standard errors of the total marginal effects is highly complicated if not impossible. Hence, the standard error is usually estimated using the delta method,23 which involves the variance-covariance matrices of the estimates from both equations. This additional complication makes it undesirable to separately estimate the two equations because obtaining the covariance of the two sets of estimates and manually combining the variance-covariance remains a challenge. Modern statistics software such as Stata have routines to estimate TPMs coefficients in cross-sectional settings in one step.13 In fact, the Stata routine even estimates the total marginal effects and their standard errors in cross-sectional settings.13
in both the first part and the second part, but also the standard error estimation of the total marginal effects should incorporate the uncertainty in both equations. The closed form solution of the standard errors of the total marginal effects is highly complicated if not impossible. Hence, the standard error is usually estimated using the delta method,23 which involves the variance-covariance matrices of the estimates from both equations. This additional complication makes it undesirable to separately estimate the two equations because obtaining the covariance of the two sets of estimates and manually combining the variance-covariance remains a challenge. Modern statistics software such as Stata have routines to estimate TPMs coefficients in cross-sectional settings in one step.13 In fact, the Stata routine even estimates the total marginal effects and their standard errors in cross-sectional settings.13
When unobserved individual-specific random effects are accounted for in the TPM using panel data, the model specification would be
(7) (8)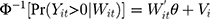
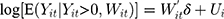
where 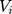 and
and 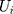 are the random intercepts in the two equations for the ith individual and were assumed to be uncorrelated with
are the random intercepts in the two equations for the ith individual and were assumed to be uncorrelated with 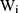 . To our knowledge, there are currently no routines in any package to estimate the TPMs with random effects. Several potential approaches to estimate TPMs with random effects have been proposed. Olsen and Schafer24 used a logistic model first part and an OLS second part, and assumed the random intercepts to be jointly normally distributed. Tooze, Grundwald, and Jones proposed a similar approach but used a log-transformed linear model for the second part.25 However, both of these approaches not only required manual assembly of the likelihood function but also lacked the capacity to accommodate GLMs in the second part. More recently, Liu et al extended the previous approaches and developed the likelihood function for the TPMs in which the first part was a logistic regression and the second part was a GLM with a generalized gamma distribution.26 In their approach, the unobserved individual-specific random effects also had a joint normal distribution. Like the previous approaches, the approach proposed by Liu et al required setting up the likelihood function manually. In addition, all the methods proposed so far did not mention how to obtain the marginal effects and the standard errors of the marginal effects following the coefficient estimation. In this study, we propose to implement TPMs with random effects as generalized structural equation models (GSEMs) that are easy to implement and can estimate marginal effects and their standard errors without sophisticated additional steps, which are described with more details in the methods section.
. To our knowledge, there are currently no routines in any package to estimate the TPMs with random effects. Several potential approaches to estimate TPMs with random effects have been proposed. Olsen and Schafer24 used a logistic model first part and an OLS second part, and assumed the random intercepts to be jointly normally distributed. Tooze, Grundwald, and Jones proposed a similar approach but used a log-transformed linear model for the second part.25 However, both of these approaches not only required manual assembly of the likelihood function but also lacked the capacity to accommodate GLMs in the second part. More recently, Liu et al extended the previous approaches and developed the likelihood function for the TPMs in which the first part was a logistic regression and the second part was a GLM with a generalized gamma distribution.26 In their approach, the unobserved individual-specific random effects also had a joint normal distribution. Like the previous approaches, the approach proposed by Liu et al required setting up the likelihood function manually. In addition, all the methods proposed so far did not mention how to obtain the marginal effects and the standard errors of the marginal effects following the coefficient estimation. In this study, we propose to implement TPMs with random effects as generalized structural equation models (GSEMs) that are easy to implement and can estimate marginal effects and their standard errors without sophisticated additional steps, which are described with more details in the methods section.
Methods
Data
The present analysis used data from the 2011, 2013 and 2015 waves of CHARLS. CHARLS is an aging survey of 45 years and older Chinese and their spouses in China that used a multistage probability sampling to allow nationally representative estimates.3,10,11 In the survey, respondents were asked about 1) socioeconomic information including age, sex, education, residence (rural or urban), income, total household consumption, and health insurance status; 2) health information including self-reported general health, thirteen physician-diagnosed chronic conditions, memory problem, had any hospitalization in the past year, had any outpatient visit in the past month, and household out-of-pocket healthcare expenditure; and 3) behavioral questions including smoking status and alcohol ingestion frequency. More information on CHARLS has been described elsewhere.10,27 To investigate the properties of PHI as supplemental insurance, we used the subsample that had public health insurance coverage at all interviews in this analysis. Household consumption and health care expenditures were only asked of the family respondents who were the family members that answered household questions on behalf of their families. In addition, we excluded the responses that reported non-positive or missing total household consumption. Hence, the final analytical sample was not necessarily a balanced panel because a response of certain individuals might have been excluded from analyses while the rest responses of the same individuals might have been included.
Empirical methods
We examined the association between supplemental PHI and household OOP healthcare expenditure as percentage of total household consumption. To that end, we estimated a TPM with random effects using the probit-GLM framework and proposed a GSEM approach to implement the estimation. Based on equations (7) and (8), our specification of the model was the following:
(9) (10)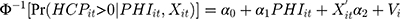
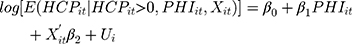
where (11)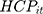 is OOP healthcare expenditure as percentage of total household consumption,
is OOP healthcare expenditure as percentage of total household consumption, 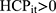 means having any OOP household healthcare expenditure,
means having any OOP household healthcare expenditure, 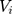 and
and 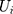 carry the same meaning as in equations (7) and (8), and
carry the same meaning as in equations (7) and (8), and 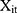 is a vector of controlled variables. Specifically,
is a vector of controlled variables. Specifically, 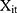 represented 1) age; 2) whether the respondent’s residence area was rural; 3) annual income (in ¥1000); 4) health information including a self-reported general health variable and indicators of thirteen chronic diseases; and 5) health-related risk behavior including smoking and alcohol ingestion frequency (daily or more often). The self-reported general health question had five categories (1 excellent, 2 very good, 3 good, 4 fair, 5 poor). When conducting the regression analyses, we created a general health indicator variable for fair or better health status because the median category was fair. The indicator for rural residence area was the only time-invariant variable we included. Sex and education were also attempted to be included as time invariant variables. However, including these variables led to multicollinearity and failure of identification. Hence, sex and education were not included in the regressions. Again, equation (9) is a probit model and equation (10) is a GLM with a gamma distribution and a log link. Following the rationale of random effects models, our identifying assumption was that
represented 1) age; 2) whether the respondent’s residence area was rural; 3) annual income (in ¥1000); 4) health information including a self-reported general health variable and indicators of thirteen chronic diseases; and 5) health-related risk behavior including smoking and alcohol ingestion frequency (daily or more often). The self-reported general health question had five categories (1 excellent, 2 very good, 3 good, 4 fair, 5 poor). When conducting the regression analyses, we created a general health indicator variable for fair or better health status because the median category was fair. The indicator for rural residence area was the only time-invariant variable we included. Sex and education were also attempted to be included as time invariant variables. However, including these variables led to multicollinearity and failure of identification. Hence, sex and education were not included in the regressions. Again, equation (9) is a probit model and equation (10) is a GLM with a gamma distribution and a log link. Following the rationale of random effects models, our identifying assumption was that 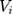 and
and 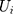 were uncorrelated with
were uncorrelated with 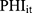 conditional on
conditional on 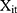 . We simultaneously estimated equations (9) and (10) of the TPM with random effects as a GSEM of which the structure is illustrated in Figure 1. GSEM can be used to estimate a series of correlated equations simultaneously. One of the important features of GSEM is that some or all of the equations in the structure can take nonlinear forms, such as probit and GLM.28 Hence, a TPM can be implemented using the GSEM approach by specifying the equations the same way as the preferred TPM framework. Another important feature is that some equations in the structure are allowed to use subsamples yet all the equations can still be estimated simultaneously.28 For example, GSEM can be used to estimate a Heckman sample selection model of which the first equation used the full sample for the analysis of selection and the second equation used a subsample of the first equation for the analysis of the intensity of the continuous part.28 This feature is also desirable in the estimation of TPMs because a TPM resembles a Heckman model in that the second equation uses a subsample of the first equation. A third important feature that can specifically be exploited by a TPM with random effects is that individual-level random effects can be specified as latent variables.28 The first and the second features allow the GSEM to estimate a conventional TPM, but the third feature additionally enables the GSEM to estimate a TPM with random effects. In the GSEM, the individual-specific random effects,
. We simultaneously estimated equations (9) and (10) of the TPM with random effects as a GSEM of which the structure is illustrated in Figure 1. GSEM can be used to estimate a series of correlated equations simultaneously. One of the important features of GSEM is that some or all of the equations in the structure can take nonlinear forms, such as probit and GLM.28 Hence, a TPM can be implemented using the GSEM approach by specifying the equations the same way as the preferred TPM framework. Another important feature is that some equations in the structure are allowed to use subsamples yet all the equations can still be estimated simultaneously.28 For example, GSEM can be used to estimate a Heckman sample selection model of which the first equation used the full sample for the analysis of selection and the second equation used a subsample of the first equation for the analysis of the intensity of the continuous part.28 This feature is also desirable in the estimation of TPMs because a TPM resembles a Heckman model in that the second equation uses a subsample of the first equation. A third important feature that can specifically be exploited by a TPM with random effects is that individual-level random effects can be specified as latent variables.28 The first and the second features allow the GSEM to estimate a conventional TPM, but the third feature additionally enables the GSEM to estimate a TPM with random effects. In the GSEM, the individual-specific random effects, 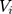 and
and 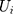 , were considered individual-specific latent variables that had a joint normal distribution conditional on the observed variables:28
, were considered individual-specific latent variables that had a joint normal distribution conditional on the observed variables:28
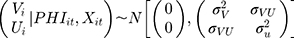
With that, it is possible to identify the parameters of the structure using maximum likelihood by including the conditional density functions of 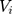 and
and 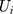 in the likelihood function. Once the coefficients were estimated, the marginal effect of the independent variables can be estimated as predictions of user-specified expressions by programming the “margins” routine in Stata to calculate the corresponding formulas (eg equation 6). The “margins” routine then estimated the standard errors of the predictions of user-specified expressions using the delta method (Appendix 2) as its built-in capacity. As byproducts of the TPM, the association of supplemental PHI with the probability of having any OOP household healthcare expenditure and the association of supplemental PHI with the burden of OOP healthcare expenditure among those who had any were also estimated in the first and second equations, respectively.
in the likelihood function. Once the coefficients were estimated, the marginal effect of the independent variables can be estimated as predictions of user-specified expressions by programming the “margins” routine in Stata to calculate the corresponding formulas (eg equation 6). The “margins” routine then estimated the standard errors of the predictions of user-specified expressions using the delta method (Appendix 2) as its built-in capacity. As byproducts of the TPM, the association of supplemental PHI with the probability of having any OOP household healthcare expenditure and the association of supplemental PHI with the burden of OOP healthcare expenditure among those who had any were also estimated in the first and second equations, respectively.
We also implemented two alternative estimation approaches of the same TPM framework. In the first alternative estimation approach, we separately estimated the first-stage probit and the second-stage GLM each of which incorporated individual-level random effects. A major drawback of this method was that the total marginal effects and their standard errors could not be estimated. Another drawback was that the correlation between the random effects could not be accounted for. The second alternative approach was a TPM without random effects estimated using the Stata TPM routine,13 which was able to estimate the two equations of the TPM simultaneously. However, an extra issue of the TPM routine beyond not taking into account the random effects was that it could not separately estimate the marginal effects in each of the steps although it was able to estimate the total marginal effects.
All analyses were carried out using Stata (version 15; Stata Corp, College Station, TX, USA).
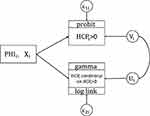 |
Figure 1 Structure of the generalized structural equation model (GSEM) used to estimate the two-part model (TPM) with random effects. |
Results
We identified 24,301 responses representing 9032 individuals that met our inclusion and exclusion criteria. Respondents reported having supplemental PHI in 480 (1.83%) of the responses. Descriptive statistics of the analytical sample are shown in Table 1. Respondents who reported having supplemental PHI were significantly younger (mean: 53.9 vs 59.3 years, p<0.001), less likely to live in rural areas (48.7% vs 66.5%, p<0.001), and less likely to be in poor self-reported health status (14.3% vs 22.5%, p<0.001). Also, PHI beneficiaries had significantly higher annual income (mean: ¥9633 vs ¥3927, p=0.001). More, the percentages of PHI beneficiaries who reported having any hospitalization in the past year (11.1% vs 11.5%, p=0.815) and having any outpatient visit in the past month (20.4% vs 20.5%, p=0.992) were similar to those of non-PHI beneficiaries. When examined descriptively, the households of the respondents who had supplemental PHI were significantly more likely to have any OOP healthcare expenditure (63.8% vs 57.2%, p=0.004) yet had a significantly lower burden of OOP healthcare expenditure (12.6% vs 15.2%, p<0.039).
 |
Table 1 Characteristics of Respondents with and Without PHI in CHARLS 2011–2015 |
The estimates of the parameter coefficients in the first-stage probit model and the second-stage GLM using the three different methods are presented in Table 2. Since the coefficients themselves do not provide inferences, they are not described here. However, it is noteworthy that the coefficients of supplemental PHI were comparable in magnitude across methods. It should also be called out that the association between supplemental PHI and the burden of OOP healthcare expenditure conditional on having any OOP healthcare expenditure in the second-stage GLM was not significant whereas it was significant in the two methods that incorporated random effects. In addition, the correlation between the random effects across the first and the second steps were not significant.
 |
Table 2 Coefficient Estimates Using the Three Different Methods to Implement TPM Estimation |
The estimates of the total marginal effects and the marginal effects in the first and second steps are listed in Table 3. The GSEM estimator showed that having supplemental PHI was associated with a higher probability [4.29 percentage points, standard error (SE): 1.69] of having any OOP healthcare expenditure, but was also associated with a lower OOP burden conditional on having any OOP healthcare expenditure (−2.37 percentage points, SE: 0.946). Overall, having supplemental PHI was insignificantly associated with a lower OOP burden (−1.05 percentage points, SE: 0.603) according to the GSEM estimates of the total marginal effects. When the probit and the GLM models with random effects were estimated separately, having supplemental PHI was also associated with a higher probability (6.99 percentage points, SE: 2.72) of having any OOP healthcare expenditure and a lower OOP burden conditional on having any OOP healthcare expenditure (−2.65 percentage points, SE: 1.33). As aforementioned, estimating the two steps with random effects separately could not generate total marginal effects. Similar to the GSEM estimate, the TPM routine estimates showed that having supplemental PHI was insignificantly associated with a lower OOP burden (−0.755 percentage points, SE: 0.929) overall. As discussed earlier, the TPM routine was not able to give marginal effects in each of the steps.
 |
Table 3 Marginal Effect Estimates Using the Three Different Methods to Implement TPM Estimation |
Most of the covariates were associated with the OOP healthcare expenditure burden in the expected direction. However, a caveat was that smoking and frequent drinking were associated with a lower OOP healthcare expenditure burden. This was likely due to omitted variable bias. For example, people who smoked and drank might have been likely to spend less frugally overall or were less concerned with health such that they were less motivated to seek healthcare. Since this was not the focus of the present study, it was not further explored.
Discussion
Using several empirical methods to analyze the CHARLS data, we did not identify any statistically significant association between having supplemental PHI and the OOP burden of healthcare expenditure. However, we did find a significant positive association between having supplemental PHI and the probability of having OOP healthcare expenditure. Also, we showed that having supplemental PHI was significantly negatively associated with the OOP burden of healthcare expenditure among those who had any healthcare expenditure. To our knowledge, the present study is the first in the literature to examine of the association of supplemental PHI with the burden of OOP healthcare expenditure in China.
To the extent that the present study did not account for potential omitted variable bias, such as the extent of financial protection from primary insurance coverage, we are not able to make causal statements based on the results. Hence, the results should only be comprehended as potentially causal, which is the foundation of our discussion. For the present study, both the overall association results and the results of each equation are important. Although the by-step estimation approach is not desirable, the inference of the results of each equation are critical for policymakers. The overall association potentially suggests that the supplemental PHI may not be sufficiently financially protective to reduce the OOP financial burden of healthcare expenditure. However, denying the value of supplemental PHI based on this observation alone can be misleading and may result in a missed opportunity of adopting supplemental PHI to improve access to healthcare and financially protecting part of the beneficiaries. In China, seeking healthcare almost always incurs OOP expenditure. Hence, a higher probability of having OOP expenditure implies greater chances of receiving healthcare. More specifically, the lack of reduced overall burden is possibly a result of increased access to healthcare and decreased intensity of OOP burden provided that the beneficiary seeks healthcare, both of which are among the most desirable features of supplemental PHI. Therefore, supplemental PHI coverage may still be able to improve the overall well-being of the beneficiaries.
Our findings have important potential implications for healthcare financing and PHI regulation in China. The strategy of the Chinese government was to encourage supplemental PHI to address the unmet need of healthcare that basic insurance schemes do not provide.7 To that end, the government deployed tax incentives to motivate the uptake of PHI.29 Based on the current results, supplemental PHI may be able to effectively improve access to healthcare while keeping the OOP healthcare expenditure burden flat. Hence, the strategy is potentially feasible to improve the overall healthcare of the population. In that regard, policies including the tax incentives should be encouraged to increase supplemental PHI coverage.
However, several issues related to supplemental PHI remain to be investigated. First, whether the increased probability of incurring healthcare services is a result of moral hazard or improved access for those who are in need cannot be ascertained. Evidence in this aspect is necessary to confirm the social efficiency of supplemental PHI before any conclusions can be drawn on the utility of supplemental PHI. Second, risk selection in the supplemental PHI market in China needs to be clarified in future research to understand who will likely benefit from tax deduction incentives. If the relatively high-income and low-risk population are more responsive to such incentives, then supplemental PHI may not be able to fulfil its role in the healthcare system. Last but not least, why supplemental PHI is not associated with a lower overall OOP burden should be shed light on, following which PHI may be regulated to work effectively in that aspect.
We consider using GSEM to estimate TPM with random effects an important contribution of the present study. Exploiting the GSEM functionality to estimate TPM with random effects has at least three advantages. First, not only random effects in both equations but also their correlation were incorporated in the estimation. Although the correlation was not statistically significant in the present analysis, this should not be generalized to all TPM with random effects. Even though the unbiasedness of estimates are unaffected if random effects are unaccounted for, the efficiency of the estimates can be decreased. In our analysis, incorporating random effects did result in more efficient estimates than ignoring them. More specifically, PHI was estimated to be significantly associated with a lower OOP burden in the second step according to both the GSEM estimates and the separate estimates of the TPM with random effects, whereas the association was not significant in the TPM model without random effects. Second, the two equations in TPM with random effects can be estimated in one step. This feature is useful for practical reasons. For computer packages, this means the coefficient estimates and their uncertainty data in both steps can be retrieved all together to calculate additional statistics. Third, as demonstrated by our analysis, GSEM generates estimates of marginal effects in each step, total marginal effects, and the corresponding standard errors. This property of GSEM is closely related to the fact that it is estimated in one step so that all information from the estimation can be used for additional calculation. As demonstrated in our analysis, no other methods provide all these advantages.
This study has several limitations. First, we could not rule out the possibility of omitted variable bias although we used multivariate regressions with a list of control variables. In fact, omitted variable bias can be a non-trivial concern in the analysis of supplemental PHI because there is almost always self-selection due to unobserved risk attitude and, to a certain extent, financial literacy. In the present study, the groups with and without supplemental PHI were unbalanced with regard to several characteristics including age, living in a rural or urban area, education, self-reported health, and income. Such unbalance may pose a threat to our identifying assumption and cause endogeneity. Addressing endogeneity is particularly challenging in this study in which the survey was the only data source and exogenous variation to be exploited is absent. We did not use propensity score matching (PSM) to balance the characteristics because PSM requires the same identifying assumption to generate unbiased and consistent estimates as does the multivariate regression approach. Also, we did not take the fixed effect model approach to address endogeneity. This was because fixed effect estimators are biased in nonlinear models with the exception of conditional logit models and Poisson models,14,17 which was discussed in the introduction section. Second, the sample size of this study is relatively limited, which could result in an underpowered analysis. Given that our total marginal effect estimates of supplemental PHI were statistically insignificant, potential underpower could be a realistic concern. Third, some of the variables were based on self-report and might be subject to recall bias. Although electronic data provided by insurers could be relatively more reliable research resources, such data sources are not currently available in China to our knowledge. Finally, the granularity of the OOP healthcare expenditure information in the survey data was limited. Hence, we could not investigate the effects of supplemental PHI on high-value procedures or services that represent genuine improved access or to examine the impacts on health outcomes which are what health insurance should ultimately contribute to.
Conclusions
Current supplemental PHI in China is potentially effective at improving access to healthcare and providing financial protection to those who incur healthcare expenditure. Future studies should ascertain the causal effects of supplemental PHI. To the extent that the current findings are concerned, policies to encourage the uptake supplemental PHI are necessary.
In addition, GSEM can be used as a random-effect TPM estimator that can be relatively easily implemented and generates useful post-estimation statistics.
Data Sharing Statement
The datasets analyzed during the current study are publicly available at http://charls.pku.edu.cn/en.
Ethics and Consent Statement
The procedures followed in this study were in accordance with the ethical standards. Only de-identified secondary data which was publicly available was analyzed.
Funding
The authors did not receive any grant from funding agencies in the public, commercial, or not-for-profit sectors for the submitted work.
Disclosure
YJ reports no conflict of interest related to the submitted work. WN was a health economics and outcomes research fellow at University of Southern California when the submitted work was conducted and was an employee of Medtronic Inc. at the time of submission.
References
1. Yu H. Universal health insurance coverage for 1.3 billion people: what accounts for China’s success? Health Policy. 2015;119(9):1145–1152. doi:10.1016/j.healthpol.2015.07.008
2. Li Y, Malik V, Hu FB. Health insurance in China: after declining in the 1990s, coverage rates rebounded to near-universal levels By 2011. Health Aff. 2017;36(8):1452–1460. doi:10.1377/hlthaff.2016.1658
3. Zhang C, Lei X, Strauss J, Zhao Y. Health insurance and health care among the mid‐aged and older Chinese: evidence from the national baseline survey of CHARLS. Health Econ. 2017;26(4):431–449. doi:10.1002/hec.3322
4. Luo Y, Bossany W, Wong J, Chen C Opportunities open up in Chinese private health insurance. 2016. Available from: https://www.bcg.com/publications/2016/insurance-health-care-payers-providers-opportunities-open-up-in-chinese-private-health-insurance.aspx.
5. Ng A, Dyckerhoff CS, Then F. Private Health Insurance in China: Finding the Winning Formula. 2012.
6. Zhao J, Ng A The rise of private health insurance in China. 2016. Available from: http://www.ey.com/gl/en/industries/financial-services/insurance/ey-the-rise-of-private-health-insurance-in-china.
7. Liu H, Gao S, Rizzo JA. The expansion of public health insurance and the demand for private health insurance in rural China. China Econ Rev. 2011;22(1):28–41. doi:10.1016/j.chieco.2010.08.006
8. Preker AS, Zweifel P, Schellekens OP. Global Marketplace for Private Health Insurance: Strength in Numbers. Washington, DC: World Bank Publications; 2009.
9. Xu K, Evans DB, Kawabata K, Zeramdini R, Klavus J, Murray CJ. Household catastrophic health expenditure: a multicountry analysis. Lancet (London, England). 2003;362(9378):111–117. doi:10.1016/S0140-6736(03)13861-5
10. Zhao Y, Hu Y, Smith JP, Strauss J, Yang G. Cohort profile: the China health and retirement longitudinal study (CHARLS). Int J Epidemiol. 2012;43(1):61–68. doi:10.1093/ije/dys203
11. Liu C, Yang C, Zhao Y, et al. Associations between long-term exposure to ambient particulate air pollution and type 2 diabetes prevalence, blood glucose and glycosylated hemoglobin levels in China. Environ Int. 2016;92:416–421. doi:10.1016/j.envint.2016.03.028
12. Wu X, Li L. The motives of intergenerational transfer to the elderly parents in China: consequences of high medical expenditure. Health Econ. 2014;23(6):631–652. doi:10.1002/hec.2943
13. Belotti F, Deb P, WG M, Norton EC. twopm: two-part models. Stata J. 2015;15(1):3–20. doi:10.1177/1536867X1501500102
14. Cameron AC, Trivedi PK. Microeconometrics: Methods and Applications. Cambridge university press; 2005.
15. Greene WH. Econometric Analysis. Pearson Education India; 2003.
16. Wooldridge JM. Econometric Analysis of Cross Section and Panel Data. MIT press; 2010.
17. Greene W. The Behavior of the Fixed Effects Estimator in Nonlinear Models. New York University, Leonard N. Stern School of Business, Department of Economics; 2002.
18. Gross DJ, Alecxih L, Gibson MJ, Corea J, Caplan C, Brangan N. Out-of-pocket health spending by poor and near-poor elderly Medicare beneficiaries. Health Serv Res. 1999;34(1 Pt 2):241.
19. Goldman DP, Zissimopoulos JM. High out-of-pocket health care spending by the elderly. Health Aff. 2003;22(3):194–202. doi:10.1377/hlthaff.22.3.194
20. Xu K, Evans DB, Carrin G, Aguilar-Rivera AM, Musgrove P, Evans T. Protecting households from catastrophic health spending. Health Aff. 2007;26(4):972–983. doi:10.1377/hlthaff.26.4.972
21. Boone J. Basic versus supplementary health insurance: access to care and the role of cost effectiveness. J Health Econ. 2018;60:53–74. doi:10.1016/j.jhealeco.2018.05.002
22. Deb P, Norton EC. Modeling health care expenditures and use. Annu Rev Public Health. 2018;39:489–505. doi:10.1146/annurev-publhealth-040617-013517
23. Papke LE, Wooldridge JM. A computational trick for delta-method standard errors. Econ Lett. 2005;86(3):413–417. doi:10.1016/j.econlet.2004.07.022
24. Olsen MK, Schafer JL. A two-part random-effects model for semicontinuous longitudinal data. J Am Stat Assoc. 2001;96(454):730–745. doi:10.1198/016214501753168389
25. Tooze JA, Grunwald GK, Jones RH. Analysis of repeated measures data with clumping at zero. Stat Methods Med Res. 2002;11(4):341–355. doi:10.1191/0962280202sm291ra
26. Liu L, Strawderman RL, Cowen ME, Shih Y-CT. A flexible two-part random effects model for correlated medical costs. J Health Econ. 2010;29(1):110–123. doi:10.1016/j.jhealeco.2009.11.010
27. Chien S, Lin A, Phillps D, Wilkens J, Lee J. Harmonized CHARLS Documentation. 2017. Available from: https://g2aging.org/?section=survey&surveyid=67.
28. Acock AC. Stata Structural Equation Modeling Reference Manual: Release 15. Stata Press; 2017.
29. China State Administration of Taxation. Notice of the Ministry of Finance, the State Administration of Taxation and the China Insurance Regulatory Commission on Promoting Nationwide Pilot Policies for Individual Income Tax on Commercial Health Insurance. Beijing, China; 2017.
 © 2020 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2020 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
