Back to Journals » Clinical Epidemiology » Volume 7
The optimal hormonal replacement modality selection for multiple organ procurement from brain-dead organ donors
Authors Mi Z, Novitzky D, Collins J, Cooper D
Received 19 July 2014
Accepted for publication 5 September 2014
Published 22 December 2014 Volume 2015:7 Pages 17—27
DOI https://doi.org/10.2147/CLEP.S71403
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Henrik Sørensen
Zhibao Mi,1 Dimitri Novitzky,2 Joseph F Collins,1 David KC Cooper3
1Cooperative Studies Program Coordinating Center, VA Maryland Health Care Systems, Perry Point, MD, USA; 2Department of Cardiothoracic Surgery, University of South Florida, Tampa, FL, USA; 3Thomas E Starzl Transplantation Institute, University of Pittsburgh, Pittsburgh, PA, USA
Abstract: The management of brain-dead organ donors is complex. The use of inotropic agents and replacement of depleted hormones (hormonal replacement therapy) is crucial for successful multiple organ procurement, yet the optimal hormonal replacement has not been identified, and the statistical adjustment to determine the best selection is not trivial. Traditional pair-wise comparisons between every pair of treatments, and multiple comparisons to all (MCA), are statistically conservative. Hsu’s multiple comparisons with the best (MCB) – adapted from the Dunnett’s multiple comparisons with control (MCC) – has been used for selecting the best treatment based on continuous variables. We selected the best hormonal replacement modality for successful multiple organ procurement using a two-step approach. First, we estimated the predicted margins by constructing generalized linear models (GLM) or generalized linear mixed models (GLMM), and then we applied the multiple comparison methods to identify the best hormonal replacement modality given that the testing of hormonal replacement modalities is independent. Based on 10-year data from the United Network for Organ Sharing (UNOS), among 16 hormonal replacement modalities, and using the 95% simultaneous confidence intervals, we found that the combination of thyroid hormone, a corticosteroid, antidiuretic hormone, and insulin was the best modality for multiple organ procurement for transplantation.
Keywords: best treatment selection, brain-dead organ donors, hormonal replacement, multiple binary endpoints, organ procurement, multiple comparisons
Introduction
The inadequate supply and quality of organs that become available from deceased humans remain major hurdles for successful organ transplantation. After brain death, hormonal alterations may result in hemodynamic instability after brain death. The use of inotropic agents and replacement of depleted hormones (hormonal replacement therapy) have helped preserve satisfactory organ function. Currently, hormonal therapy can include the administration of four hormones – thyroid hormone (triiodothyronine [T3] or levothyroxine [T4]), a corticosteroid (eg, methylprednisolone), and/or antidiuretic hormone (arginine vasopressin or DDAVP), and/or insulin, each of which can be administered alone or in various combinations.1–7
Although there are reports demonstrating that combination hormonal therapy can significantly increase the number of organs that can be procured from each brain-dead potential donor, the optimal regimen that maximizes multiple organ procurement and improves organ quality remains uncertain. In the present study, using data from the United Network for Organ Sharing (UNOS), we explored the optimal regimen from all possible combinations of the four hormones, which proved a statistically challenging exercise.
Statistically, to select the best modality from the many available hormonal replacement regimens is a multiple comparison problem. Traditional pair-wise comparison (multiple comparisons to all [MCA]) between every pair of treatments is statistically conservative. Hsu and others proposed a multiple comparison method to select the optimal treatment, known as multiple comparisons with the best (MCB), which was adapted from Dunnett’s multiple comparison with control (MCC) method by comparing each treatment with the best of the other treatments.8–12 Since it was developed, the MCB has been widely used to select the best treatment based on continuous endpoints. However, sometimes one needs to select the best treatment based on multiple endpoints, which usually are not continuous. In this report, we used a two-step method to select the best hormonal replacement modality based on six binary endpoints.
Materials and methods
Data on potential organ donors
The data analyzed were provided by UNOS (Richmond, VA, USA). A total of 71,571 potential organ donors were registered at UNOS during the 10-year period January 1, 2000 to December 31, 2009.3 Data from a subset of 40,124 deceased subjects, who were not donors after cardiac death (donation after cardiac death, DCD) and for whom complete data on the hormonal therapy administered (if any) were available, were analyzed. The data were analyzed by assessing the procurement of the following organs from each donor – heart, lungs, kidneys, liver, pancreas, and intestines. Treatment with four different hormones (with the aim of improving organ function and increasing organ procurement) was recorded and analyzed – thyroid hormone (T3 or T4), a corticosteroid, antidiuretic hormone (arginine vasopressin or DDAVP), and insulin. An individual donor could have received one or more (or none) of these four hormones. For convenience of illustration, the hormonal treatment modalities are categorized by thyroid hormone in Table 1.
Analytical methods
The transplantation rate was calculated to evaluate the efficacy of the hormonal replacement regimen on organ procurement (and subsequent successful transplantation). The successful transplantation rate for a specific organ given a specific hormonal treatment modality, was calculated as the number of organs procured/transplanted divided by all of the organ dispositions among the donors in that modality group. The data management and analysis were performed using SAS (v9.3; SAS Inc., Cary, NC, USA). Missing values were excluded from the analysis.
Estimation of predicted margins
To select the best hormonal replacement modality for organ procurement, we used a logistic regression model to estimate the predicted margins or the logits for each particular organ type, including heart, lungs, kidneys, liver, pancreas, and intestine. The logits for each type of organ were estimated based on the following model, which adjusted for age, sex, and body mass index (BMI):
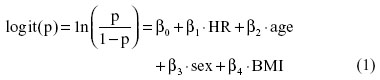
where p is the probability of successfully procuring/transplanting an organ given a specific hormonal replacement regimen.
Furthermore, we selected the optimal hormonal replacement regimen for multiple organ procurement (intestine not included in the analysis) by constructing a generalized linear mixed model to estimate least square means or LS-means, defined as follows:
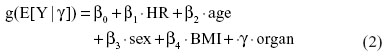
where βs are the fixed effects and γ is the random effect. Four variance–covariance structures were used to estimate the random effect, ie, variance component (VC), compound symmetry (CS), autoregressive (AR), and unstructured (UN).
Multiple comparison procedures
To select the optimal modality for single and multiple organ procurement, multiple comparison procedures (MCA, MCC, and MCB) were applied based on the logits from either the logistic regressions or generalized linear mixed models (GLMM). Let θ1, θ2, …, θk denote the treatment effect of logits estimated from the models described above. In the MCA model, the parameters of interest were θi – θj for all i ≠ j, and there were k(k – 1)/2 or 120 pair-wise comparisons. In the MCC model, the hormonal replacement modality with the highest value was used as the control and denoted as treatment c. Then the parameters of interest were δi = θi – θc for i = 1, 2, …, k–1, which in this study involved 15 comparisons. Similar to the MCC, the parameters of interest for the MCB were the difference between each hormonal replacement modality and the true best of the others. For a specific hormonal replacement modality i with an unknown real value θi, the ordered kth treatment effect was θ[k] = max1≤i≤kθi. If modality i is preferred to modality j when θi > θj, the parameters δi = θ [k] – θi reflect inversely the success of each treatment relative to the best treatment for i = 1, 2, …, k. The simultaneous confidence intervals on the parameters of interest for the multiple comparison procedures were constructed to assess efficacy for each hormonal modality for individual and multiple organ procurement. The Tukey MCA procedure was used for all pair-wise comparisons,13 and the Dunnett–Hsu MCC and the Hsu MCB procedures were used to select the best modality based on the largest mean logits or LS-means.
Results
The best hormonal replacement modality selection was based on single organ type procurement and multiple organ procurement, including the average number of multiple organ procurements for each individual brain-dead organ donor.
General information on organ procurements
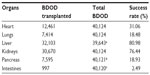
For each brain-dead potential organ donor, there were six specific organs that could be procured (and transplanted). Table 2 lists the overall success rates for each organ type procured (and transplanted) without specifying the hormonal replacement information. Procurement of the liver or kidneys had higher success rates (80.98% and 76.44%, respectively) than that of heart, pancreas, or lungs (31.06%, 18.93%, and 18.48%, respectively). Procurement of intestines had the lowest success rate (2.49%), but this was almost certainly related to the reduced need for intestinal transplantation compared with transplantation of other vital organs.
The optimal hormonal replacement regimen based on individual organ procurement
Generally, multiple organs are procured from each donor. In order to assess whether a certain hormonal replacement modality proved beneficial for a specific organ, but not for others, we determined the optimal modality for each specific organ, eg, the heart. Figure 1 shows predicted margins or LS-means estimated from logistic regressions based on the success rates for procurement of different organs across the 16 hormonal treatment categories, ie, 15 hormonal treatment modalities and one in which no hormonal therapy was administered. The largest LS-mean of the modalities was identified for each organ type. The effects of hormonal replacement therapy were reflected by the values of the predicted population margins or LS-means. The higher the value, the better the effect. The simultaneous confidence intervals for LS-mean differences between each modality and the modality with the largest LS-mean value are shown in Figure 2.
When the Dunnett procedure was used, the best hormonal replacement modalities for procurement of heart, lungs, liver, kidneys, pancreas, and intestines were A4, A1, B2, A1, A2, and A2, respectively. However, the best modality A4 for heart procurement was not significantly better than A1, A2, and A3. Similarly, A1 was not significantly better than A4 for kidneys procurement, and A2 was not significantly better than A4 for intestine procurement (Figure 2). When the Hsu MCB procedure was used, the best modalities for heart, lungs, liver, kidneys, pancreas, and intestines were A4, A1, B2, A1, A2, and A2, respectively. As shown in Figure 3, the results were similar to those when the Dunnett MCC procedure was used; where the optimal hormonal therapy, A4, was not significantly better than A1, A2, and A3 for heart procurement, A1 was not significantly better than A4 for kidneys procurement, and A2 was not significantly better than A4 for intestine procurement.
The optimal hormonal replacement regimen based on multiple organ procurement
There were two parameters used for selection of the best modality for multiple organ procurement/transplantation, ie, average number of organs procured from an individual donor and the success rate for multiple organ procurement.
This approach was based on the LS-means estimated from the GLMM using four covariance structures for estimating the random effect. As shown in Table 3, though there were slight LS-mean value differences among these four covariance structure models, there were no differences in terms of the ranks of the hormonal replacement effect, and group A1 was the top rank of all four models. Pair-wise comparisons were performed using the Tukey–Kramer procedure. The results showed that group A1 was the best modality; however, it was not significantly better than many other groups, such as A2, A3, and A4, after the Tukey–Kramer adjustment (Figure 4).
  | Table 3 LS-means estimated from different covariance structure models |
When the Dunnett–Hsu procedure was used to construct the simultaneous confidence intervals or 95% decision limits, the results were similar to those when pair-wise comparisons were performed. A1 was the best modality for multiple organ procurement (Figure 5), but was not significantly better than A2 and A4.
Group A1 was also identified as the best treatment modality using the average number of organs procured for each donor based on the general linear models with or without adjusting the covariates, age, sex, and BMI. As shown in Figure 6, group A1 was the best modality using both Dunnett–Hsu MCC and Hsu MCB procedures. However, without the covariate adjustment, group A1 was not significantly better than A2, A3, or A4 when the MCC was used, and similar results were observed when the MCB was used, whereas, after the covariate adjustment, A1 was the best modality when MCC was used, but A1 was not significantly better than A2, A3, or A4 when the MCB was used.
The detailed hormonal replacement combinations for each organ type and multiple organ procurement are summarized in Table 4.
Discussion
Hormonal replacement therapy has been widely used to increase organ procurement from human brain-dead donors. To date, there has been no conclusive research indicating the optimal hormonal combinations for procurement of a specific type of organ or of multiple organs. In the present study, we proposed a two-step approach using generalized linear models (GLM) or GLMM, and multiple comparison procedures. Using Tukey’s MCA, Dunnett–Hsu’s MCC, and Hsu’s MCB, we analyzed data from 40,124 brain-dead potential donors (in which definitive hormonal replacement therapy was documented) with the aim of identifying the optimal therapy for both individual and multiple organ procurement.
We determined that thyroid hormone (T3 or T4), a corticosteroid, and antidiuretic hormone played important roles in the management of the donor if organ procurement (and transplantation) was to be maximized. Although there was some variation in the optimal combination of hormones for a specific organ, the combination of thyroid hormone, a corticosteroid, antidiuretic hormone, and insulin was the optimal hormonal therapy to maximize multiple organ procurement. Insulin played a relatively minor role, and might even be detrimental to procurement of the pancreas.3
To select the best modality, we applied multiple comparison methods to control type I error rates. Tukey’s MCA is the most powerful test when performing all pair-wise comparisons and Dunnett’s MCC is the most powerful test when comparing to a “control”; whereas Hsu’s MCB is the most powerful test when not requiring all pair-wise comparisons, which compares between each sample mean and the “best” of all the other means, where one specifies that “best” means either largest or smallest. It is a modification of Dunnett’s MCC method by treating the “best” as an unknown parameter. The purpose is to select which group(s) is/are the best, ie, not significantly different from each other, but significantly better than the others. In this data analysis, we yielded similar results using the three methods because of the large sample size. We applied the Dunnett–Hsu MCC by treating the highest value by treatment effect as the “control” group, and testing whether the other treatment effects were inferior to the “control”, which then we considered as the best modality, as a comparison with the results from the Hsu MCB. The best hormonal replacement selections were based on the simultaneous confidence intervals using both MCC and MCB procedures since Tukey’s MCA is too conservative in the optimal treatment selection.
There are several limitations to our study, most of which were unavoidable. For example, the study was retrospective, and the UNOS database is largely unaudited and may contain minor inaccuracies. The reasons why an organ may not have been procured were not known to us though, in a study of such a large number of potential donors, this factor should not have played a significant role. It was also unknown to us whether hormonal therapy was administered as part of a routine protocol or because the donor’s hemodynamic status was deteriorating. Antidiuretic hormone is administered to any donor with diabetes insipidus, which is almost ubiquitous after brain death, whereas T3/T4 may only be given when hemodynamic status is poor. Data on inotropic support and the dosage of the hormones administered were not uniformly recorded. It was also uncertain to us whether the donor organs had been affected by such factors as a period of cardiac arrest or previous cocaine use. Nevertheless, though a prospective randomized study would carry greater scientific value, we believe the current retrospective analysis has sufficient statistical power to allow conclusions to be drawn.
Certain questions are raised by our results. For example, why was procurement of livers not increased by thyroid hormonal therapy? We have attempted to address this point elsewhere.14 In brief, we note that livers were procured from a significantly greater number of donors (>80%) than any other organ (if a pair of kidneys or lungs is considered as a single organ) (P<0.0001) irrespective of the hormonal treatment that the donor received. This suggests that the liver (even when the donor is untreated) is perhaps more resistant to brain death–associated injury than other organs, as it may have a greater adaptability to chemical, nutritional, and immunogenic stimuli than other vital organs. However, we remain uncertain why corticosteroids did not appear always beneficial to procurement of the heart, but this may possibly be related to the fact that T3/T4 is particularly effective in increasing myocardial energy stores and in reducing the inflammatory response, which may negate the weaker effect provided by corticosteroids.
The present paper, however, was primarily directed at the statistical methods that might be optimal to determine the effect of the various hormones available for treatment of potential organ donors by appropriately controlling type I error. Based on the available UNOS data, and using the proposed best treatment selection method, we cautiously recommend that the combination of all four hormones is the optimal modality for multiple organ procurement for transplantation. However, our goal is to extend the method to improve selection of the best treatment or intervention in clinical and epidemiological studies.
Acknowledgment
The authors thank the United Network for Organ Sharing (UNOS) for sharing their database.
Disclosure
The authors report no conflicts of interest in this work.
References
Novitzky D, Wicomb WN, Rose AG, Cooper DK, and Reichart B. Pathophysiology of pulmonary edema following experimental brain death in the chacma baboon Ann Thorac Surg. 1987;43(3):288–294. | |
Novitzky D and Cooper DK. Thyroid hormone and the stunned myocardium. J Endocrinol. 2014; 223(1):R1–R8. | |
Novitzky D, Mi Z, Sun Q, Collins J, Cooper DKC. Thyroid hormone therapy in the management of 63,593 brain-dead organ donors: a retrospective analysis. Transplantation. In press. | |
Novitzky D, Cooper DKC, Rosendale JD and H.M. Kauffman HM. Hormonal therapy of the brain-dead organ donor: experimental and clinical studies. Transplantation. 2006;82:1396–1401. | |
Rosendale JD, Chabalewski FL, McBride MA, Garrity ER, Rosengard BR, Delmonico FL and Kaufmann HM. Increased transplanted organs from the use of a standardized donor management protocol. Am J Transplant. 2002l; 2:761–768. | |
Rosendale JD, Kauffman HM, McBride MA, Chabalewski FL, Zaroff JG, Garrity ER, Delmonico FL and Rosengard BR. Aggressive pharmacological donor management results in more transplanted organs. Transplantation. 2003;75:482–487. | |
Cooper DK, Novitzky D, Wicomb WN, Basker M, Rosendale JD and Kauffman HM. A review of studies relating to thyroid hormone therapy in brain-dead organ donors. Front Biosci. 2009;14:3750–3770. | |
Dunnett CW. A multiple comparison procedure for comparing several treatments with a control. J Am Stat Assoc. 1955;50:1096–1112. | |
Dunnett CW. Pairwise multiple comparisons in the unequal variance case. J Am Stat Assoc. 1980;75:796–800. | |
Hsu JC. Simultaneous confidence intervals for all distances from the ‘best’. Annals of Statistics.1981;9:1026–1034. | |
Hsu JC. The factor analytic approach to simultaneous inference in the general linear model. J Comput Graph Stat.1992;1:151–168. | |
Edwards DG and Hsu JC. Multiple comparisons with the best treatment. J Am Stat Assoc. 1983;78:965–971. | |
Tukey JW. The problem of multiple comparisons. Unpublished manuscript, 1953. In The Collected Works of John W. Tukey VIII. Multiple Comparisons: 1948–1983 1–300. Chapman and Hall, New York. | |
Novitzky D, Mi Z, Videla LA, Collins JF, Cooper DKC. Effects of thyroid hormone therapy on procurement of abdominal organs from brain-dead donors. (Unpublished manuscript). |
 © 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.