Back to Journals » Cancer Management and Research » Volume 13
Prediction of Risk Factors for Pathological Fracture After Bone Tumor Biopsy Using Finite Element Analysis
Authors Iwai T , Hoshi M, Oebisu N, Orita K, Shimatani A, Takada N, Nakamura H
Received 24 February 2021
Accepted for publication 26 April 2021
Published 12 May 2021 Volume 2021:13 Pages 3849—3856
DOI https://doi.org/10.2147/CMAR.S307586
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Sanjeev K. Srivastava
Tadashi Iwai, Manabu Hoshi, Naoto Oebisu, Kumi Orita, Akiyoshi Shimatani, Naoki Takada, Hiroaki Nakamura
Department of Orthopedic Surgery, Osaka City University Graduate School of Medicine, Osaka, 545-8585, Japan
Correspondence: Tadashi Iwai
Department of Orthopedic Surgery, Osaka City University Graduate School of Medicine, 1-4-3 Asahi-Machi, Abeno-Ku, Osaka, 545-8585, Japan
Tel +81-6-6645-3851
Fax +81-6-6646-6260
Email [email protected]
Purpose: We aimed to determine if finite element analysis (FEA) provides useful thresholds for bone biopsy practice patterns.
Methods: The femoral head compression test was performed on rabbit femurs, using FEA to identify the part of the bone that preferentially fractures (n=15/group). Four types of rectangular biopsy holes were made using finite element (FE) models. These models were divided into control (no defect), defect 1 (10% width), defect 2 (20% width), defect 3 (30% width), and defect 4 (40% width) groups (n=15 each). Three types of rectangular biopsy holes (defect A, 27% length; defect B, 40% length; defect C, 53% length) were also made using FE models (n=15 each). The load to failure was then predicted using FEA.
Results: Almost all femurs with no defect were fractured at the femoral shaft in both the femoral head compression test and FEA. The experimental load to failure in intact femurs was predicted well by the FE models (R2=0.74, p< 0.001). There was also a strong linear correlation of stiffness between compression test in femurs with no defect and the FEA (R2=0.68, p< 0.001). Therefore, the femoral shaft was targeted for FEA. The median predicted loads by FEA were significantly higher for defect 1 than for the other types when testing the widths of the rectangular defects, but there were no significant differences among the three types when testing for defect length.
Conclusion: The FEA results correlated well with those of the femoral head compression test. A width < 10% of the circumference length in bone biopsy holes helps minimize bone strength reduction using FEA. It may be useful for orthopedic doctors to perform FEA to avoid pathological fractures after bone tumor biopsy.
Keywords: femur, orthopedics, bone tumor biopsy, New Zealand white rabbits, finite element analysis
Introduction
Bone tumors are relatively rare and comprise a wide range of various histological types.1 Malignant bone tumors need to be diagnosed pathologically to determine the treatment strategy. Orthopedic oncologists usually make a biopsy hole in the cortex wall of the affected bone and then obtain a piece of the tumor tissue.2 However, there are certain complications associated with bone biopsy, such as massive bleeding and malignant tumor contamination due to pathological fractures.2,3
Regarding pathological fractures, orthopedic oncologists often use the Mirel scoring system for predicting fractures in X-ray images.4 The Mirel criteria have been demonstrated to be 91% sensitive but only 35% specific.5 Therefore, Van der Linden et al indicated that a bone lesion with an axial cortical involvement >30 mm in computed tomography (CT) imaging had a high risk of fractures and should be stabilized surgically.6 Tatar et al also reported in a clinical retrospective study that surgical treatment should be considered when the ratio of the circumferential cortical lysis to the circumferential perimeter of the bone in CT imaging is greater than 30%.7 Recently, finite element analysis (FEA) based on CT imaging has also been reported to play an important role in assessing the risk of pathological fractures due to bone metastases.8
However, a few reports have discussed bone strength following bone biopsy, and there have been only minimal experimental investigations using human cadavers or animal bone models.9,10 To the best of our knowledge, there have been no similar experimental studies concerning bone strength after bone biopsy using FEA. It is essential to decrease the risk of pathological fracture resulting from the bone biopsy procedure. The optimal shape for a bone tumor biopsy has been shown to be rectangular.11 Moreover, it was previously found that the width of the biopsy hole for bone tumor biopsy is related to pathological fractures.12 Although it has been established through rabbit femoral head compression testing that the width of the defect is related to the fragility of the affected bone, we were unable to validate whether the experimental value correlates well with the FEA value. Therefore, we hypothesized that FEA may also provide a useful threshold for orthopedic doctors regarding bone biopsy practice patterns. This study aimed to determine if FEA provides useful thresholds for performing bone biopsy.
Materials and Methods
Animals
Eight female New Zealand white rabbits aged 1–2 years, weighing between 3500 and 4500 g, were purchased from SLC Japan (Shizuoka, Japan) and housed individually with free access to food and water. They were euthanized with an overdose of pentobarbitone sodium (800 mg/kg) administered intravenously, and their hind limbs were dissected. The femoral head compression test was performed on rabbit femurs, using FEA to identify the part of the bone that preferentially fractures (n=15/group). All animal experiments were carried out in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. The present study was approved by our institutional review board (no. 17031, Laboratory Animal Center, Graduate School of Medicine, Osaka City University). Furthermore, all procedures performed on animals complied with the Animal Research: Reporting of the ARRIVE guidelines.
Nonlinear FEA Prediction
Axial CT scans of the entire rabbit femurs were obtained on a single-slice helical scanner (Prospeed AI; GE Healthcare, London, UK); slice thickness was 0.5 mm. A calibration phantom (QRM-BDC; QRM, Möhrendorf, Germany) containing three hydroxyapatite rods (0, 100, and 200 mg/cm3) was tested together with the specimen in water. Three-dimensional FE models of the femurs were developed using the CT data from Mechanical Finder version 9.0, standard edition (Research Center of Computational Mechanics, Inc., Tokyo, Japan), which reconstructs individual bone shapes and density distributions. All femoral trabecular bone and inner parts of the cortex were meshed using linear tetrahedral elements with a global edge length of 0.6 mm. The outer surface of the cortical bone was modeled using three nodal-point shell elements with a thickness of 0.3 mm. The CT value of each element was set as the average of the voxels contained in one element. Mechanical properties of each element were calculated in Hounsfield units (HU).13
Previous reports had used Kayak’s equation for FEA; therefore, we also used this equation.13
The following specific equations were used:
Young’s modulus (E, MPa).
E= 0.001 (ρ=0)
E = 33,900 ρ2.20 (0 < ρ ≤ 0.27)
E = 5307 ρ + 469 (0.27 < ρ < 0.6)
E = 10,200 ρ2.01 (0.6 ≤ ρ)
Yield stress (σ, MPa).
σ = 1.0×1020 (ρ ≤ 0.2)
σ = 137 ρ1.88 (0.2 < ρ < 0.317)
σ = 114ρ1.72 (0.317 ≤ ρ)
Modulus values <0.01 MPa were designated as 0.01 MPa, whereas those >20 GPa were designated as 20 GPa.14 The Young’s modulus and yield stress of the shell element were calculated, assuming its CT value was 1000 HU. The Drucker–Prager equivalent criterion was adopted for the yield of the element.15 The tensile yield stress was assumed to be 0.8 times the compressive yield stress in agreement with a previous study.16 Poisson’s coefficient for each element was set at 0.3.17
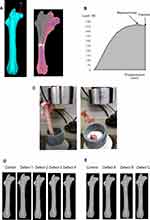
To reproduce real mechanical testing, the FEA model was set as similar to the mechanical test as possible (Figure 1A). The FE-predicted fracture load (in newtons) was defined as the load when the displacement sharply increased. The FE-predicted stiffness (in newtons/mm) was also calculated as the slope of the load-displacement curve between 20 and 80% of the FE-predicted fracture load (Figure 1B).
Experiment 1
A femoral head compression test was conducted using EZ Graph (Shimadzu Corp., Kyoto, Japan) (Figure 1B). Femur specimens were kept in a freezer at –20°C until analyzed. A femoral head compression test was set up using upper and lower jigs and a cylindrical holder and oriented so that the femur was vertical in the sagittal plane, valgus in the frontal plane, and slightly extroverted in the coronal plane. The lower part of the femur was completely fixed in a polyvinyl chloride pipe using epoxy resin. The femoral valgus angle was 9°. The upper jig that was in contact with the femoral head was designed to be flat. The upper jig was designed in such a way that any interference with the femur diaphysis during the compression test was avoided (Figure 1C).
Before mechanical testing, the femurs were removed from frozen storage and saturated in tepid saline while being kept moist (for consistency). A compression load was applied at a rate of 10 mm/min. The direction of the compression was parallel to the mechanical axis. The compression test was performed until the femur specimens fractured. The magnitude of the applied load and displacement was continuously recorded. From the test results, maximum load and stiffness (a slope between 20 and 80% of the maximum load) were calculated (Figure 1B). In this mechanical testing, the maximum load was defined as the fracture load. The location of the fracture was also recorded. We compared the relationship of fracture load and stiffness between the compression test and FEA.
Experiment 2
Based on the results of experiment 1, the location of bone fenestration was decided to be the femoral shaft in the FE models. The FE models were assigned to four groups of 15 each. The FE models included various types of rectangular defects of the same length at the same site on the femoral shaft. In each of the FE models, holes of four different widths were virtually created at the distal 1.5 cm of the lesser trochanter on the anterior surface of the femoral shaft. Defects 1–4 were 2.6–3.0 × 12 mm (10% of the circumference), 5.2–6.0 × 12 mm (20% of the circumference), 7.8–9.0 × 12 mm (30% of the circumference), and 10.4–12.0 × 12 mm (40% of the circumference) rectangular holes (Figure 1D).
The FE-predicted fracture load was defined as the load when the displacement sharply increased.
Experiment 3
The FE models were assigned to three groups of 15 each. The three groups included various types of rectangular defects of the same width at the same site on the femoral shaft. In each of the FE models, holes of three different shapes were also virtually created at the distal 1.5 cm of the lesser trochanter on the anterior surface of the femoral shaft. Defects A–C were 2.6–3.0 × 12 mm (10% of the circumference × 27% of the diaphyseal length), 2.6–3.0 × 18 mm rectangular hole (10% of the circumference × 40% of the diaphyseal length), and 2.6–3.0 × 24 mm (10% of the circumference × 53% of the diaphyseal length) rectangular holes (Figure 1E).
The FE-predicted fracture load was defined as the load when the displacement sharply increased.
Statistical Analysis
The relationship between the experimental fracture load and the FE-predicted fracture load was calculated using simple linear regression analysis. The strength of the relationship was determined by considering the coefficient of determination and their significance. The Kruskal–Wallis test with the Steel–Dwass test for multiple comparisons was performed to compare the four or five groups in terms of fracture load (in newtons). Statistical analysis was performed using IBM SPSS Statistics (SPSS 26.0, IBM, Corp., Armonk, NY, USA) and Excel statistical software package (Ekuseru-Toukei 2015; Social Survey Research Information Co., Ltd., Tokyo, Japan). P-values <0.05 were considered statistically significant.
Results
Experiment 1
The median FE-predicted and experimental fracture loads were 453 (396.5–741) and 490 (376.5–672) N, respectively (Table 1 and Figure 2A). Fourteen of the 15 femurs were fractured at the femoral shaft in the femoral head compression test, whereas all the 15 femurs were predicted to be fractured at the femoral shaft in FEA (Table 1). The experiment load to failure for intact femurs was well predicted by the FE models (R2=0.74, p<0.001) (Figure 2A). Furthermore, there was a strong linear correlation between the experimental stiffness and the FE-predicted stiffness (R2=0.68, p<0.001) (Figure 2B).
 |
Table 1 Results of Experiment 1 |
Experiment 2
The median FE-predicted fracture loads were 453 (396.5–741) N for the control (no defect), 409 (389.5–707) N for defect 1 (10% width), 299 (259–383.5) N for defect 2 (20% width), 231 (195–283) N for defect 3 (30% width), and 187 (160–201) N for defect 4 (40% width) (Figure 2C). The FE-predicted fracture load of defect 1 was significantly higher than that of defects 2 (p=0.0099), 3 (p<0.001), and 4 (p<0.001). There was no significant difference between the FE-predicted fracture load of the control (no defect) and defect 1 (p=0.74).
Experiment 3
The median FE-predicted fracture loads were 453 (396.5–741) N for the control (no defect), 409 (389.5–707) N for defect A (27% length), 401 (377–582) N for defect B (40% length), and 377 (354–496) N for defect C (53% length) (Figure 2D). Regarding the FE-predicted fracture load, there were no significant differences among defects A (p=0.51), B (p=0.26), and C (p=0.64).
Discussion
Biopsy is an essential tool not only for histological confirmation but also for subsequent therapeutic strategies; thus, it is useful to find a solitary bone lesion with unusual radiological features suggesting malignancy.2 During bone biopsy, a hole is often made in the cortex wall of the bone affected by the tumor. However, weakening of the bone may occur following the procedure.2 The weakened bone causes pathological fractures, which could lead to malignant tumor contamination that can then spread rapidly.2 It is not easy to judge the surgical safety margin radiologically; therefore, a wider margin of normal tissue, including the malignant tumor, must be resected.18,19 Moreover, it would be complicated to remove the malignant tumor along with the pathological fracture. Motor function is dramatically reduced after a major surgical procedure for a pathological fracture in cases of malignant tumors, which negatively impacts the quality of life.20 Previous reports have indicated a close relationship between pathological fracture and poor survival rates.20 Post-treatment fractures also have negative effects, even in cases of benign bone tumors.21 Therefore, bone biopsy must be performed as safely as possible. There have been few reports on experimental studies of bone tumor biopsy parameters for avoiding pathological fractures. Clerks introduced the relationship between biopsy hole shape and size in 1977.9
We also demonstrated that the optimal shape of the bone tumor biopsy hole using the rabbit femoral head compression test was a rectangle with narrow width.11 Furthermore, it was established by the rabbit femoral head compression test that the width of the defect is related to the fragility of the affected bone.12 Nevertheless, we were unable to determine whether the numerical value of the compression test and the part of the femur anatomically fractured were correlated with those of FEA.
We planned to perform the femoral head compression test from the femoral head to the direction of the mechanical axis by assuming bipedal walking as the method of the present study, as in a previous report.11,12 Although there is controversy regarding the preferential anatomical site of the femur during pathological fracture in patients, we confirmed that the numerical value by the compression test and the part of the femur anatomically fractured were well correlated with that by the FEA in experiment 1 (Table 1 and Figure 2A and B). Furthermore, we created four types of rectangular biopsy holes virtually in the cortical wall of the rabbit femur to identify the optimal width of the bone tumor biopsy using FEA in experiment 2: defect 1 (10% width), defect 2 (20% width), defect 3 (30% width), and defect 4 (40% width), and we compared the results of the control (no defect) to those of defects 1, 2, 3, and 4. We also virtually created three types of rectangular biopsy holes for bone tumor biopsy: defect A (27% length), defect B (40% length), and defect C (53% length); we then compared the results of the control (no defect) with those of defects A, B, and, C.
There were strong correlations between mechanical testing and FEA prediction for both fracture load and stiffness in this study (Figure 2A and B). Based on the results of this study, we created a box-and-whisker graph in experiments 2 and 3 (Figure 2C and D). The sharp decrease in bone strength can be predicted if the width of the bone defect is greater than 10% of the circumference (Figure 2C). Moreover, the bone strength will be maintained to some extent even if the length of the bone defect is just over 50% of the diaphyseal length (Figure 2D). Therefore, a biopsy hole of rectangular shape with less than 10% width was presumed to be ideal in terms of bone strength. Furthermore, these results also correlated well with the results of compression tests in our previous report.12 However, it will also be essential for us to confirm whether the FE-predicted fracture loads on virtually created defects will be similar to experimental fracture loads on actual defects in the same rabbit femurs.
This study has some limitations. New Zealand white rabbits in this study were 1–2 years of age; therefore, there may be some differences in bone density. This may also be the reason why the results of the experiments are polarized around 400 and 800N. However, more importantly, human cadavers should have been chosen instead of animal bones based on clinical grounds. The position of the defect has a great deal of mechanical significance. This is because the lateral side is the tension side of the load, and the anterior side is perpendicular to it. Bone biopsy is often performed at the lateral side of the femoral bone clinically. Therefore, holes with the same areas on the lateral side of rabbit femurs should have been virtually made. However, even making a virtual biopsy hole on the lateral side was very difficult because of the extremely narrow surface of the bone; hence, we created the hole on the anterior side, which has a wider surface. Regarding the cortical thickness, Clerk et al reported that there was no significant change in the amount of bone removed in the same cross-section.9 Therefore, there seem to be no significant differences in bone strength between a fan and a rectangular shape. A rectangular shape with rounded ends may be ideal regarding bone strength.9 Further studies using FEA investigating the notch factor are warranted; however, it is also essential to perform bone tumor biopsy quickly because of concerns regarding tumor contamination and a large amount of blood loss. Therefore, the creation of a rectangular hole with rounded ends may be very difficult on clinical grounds. The most important limitation was that only the results of the femoral head compression test were used to verify the data. Torsion testing data should have been added to obtain more accurate results. Clinically, the material properties of bone that has been eroded by tumor cells may also differ from those of healthy material. Therefore, the mechanical strength may be reduced in addition to the strength lost in the bone biopsy. There are numerous differences between humans and rabbits because rabbits are quadrupeds, whereas humans are bipeds. On the whole, we need to determine whether the results of the present study can be adapted to those in humans by investigating CT images of patients with femoral bone tumors and conducting FEA in the future.
Conclusion
This study assessed the risk factors of pathological fracture after bone tumor biopsy using FEA. We verified that the fragility of the affected bone can be predicted by investigating bone strength using FEA. Therefore, it may be valuable for orthopedic oncologists to use FEA before performing bone biopsy. FEA also indicated that the optimal bone biopsy shape is rectangular with less than 10% of the width of the circumference in the cortex wall. If a larger amount of tumor tissue is required, the biopsy hole should be elongated longitudinally.
Abbreviations
FEA, finite element analysis; FE, finite element; CT, computed tomography; HU, Hounsfield units.
Data Sharing Statement
The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors are very grateful for the invaluable support and various discussions with other members of the Department of Orthopedic Surgery.
Funding
There is no funding source.
Disclosure
Dr Hiroaki Nakamura reports grants from Japan Society for the Promotion of Science, personal fees from DAIICHI SANKYO COMPANY, LIMITED, Taisho Toyama Pharmaceutical Co., Ltd., SHIONOGI & CO., LTD., Eli Lilly Japan K.K, outside the submitted work. The authors report no other conflicts of interest in this work.
References
1. Fletcher CDM, Bridge JA, Hogendoorn PCW, Mertens F. WHO Classification of Tumours of Soft Tissue and Bone.
2. Traina F, Errani C, Toscano A, et al. Current concepts in the biopsy of musculoskeletal tumors: AAOS exhibit selection. J Bone Joint Surg Am. 2015;7:e7. doi:10.2106/JBJS.N.00661
3. Casali PG, Bielack S, Abecassis N, et al. Bone sarcomas: ESMO-PaedCan-EURACAN clinical practice guidelines for diagnosis, treatment and follow-up. Ann Oncol. 2018;29(Suppl 4):79–95. doi:10.1093/annonc/mdy310
4. Mirels H. Metastatic disease in long bones. a proposed scoring system for diagnosing impending pathologic fractures. Clin Orthop Relat Res. 1989;249:256–264. doi:10.1097/00003086-198912000-00027
5. Damron TA, Morgan H, Prakash D, et al. Critical evaluation of Mirels’ rating system for impending pathologic fractures. Clin Orthop Relat Res. 2003;415:S201–207. doi:10.1097/01.blo.0000093842.72468.73
6. Van der Linden YM, Dijkstra PD, Kroon HM, et al. Comparative analysis of risk factors for pathological fracture with femoral metastases. J Bone Joint Surg Br. 2004;86:566–573. doi:10.1302/0301-620X.86B4.14703
7. Tatar Z, Soubrier M, Dillies AF, et al. Assessment of the risk factors for impending fractures following radiotherapy for long bone metastases using CT scan-based virtual simulation: a retrospective study. Radiat Oncol. 2014;9:227. doi:10.1186/s13014-014-0227-1
8. Sternheim A, Giladi O, Gortzak Y, et al. Pathological fracture risk assessment in patients with femoral metastases using CT-based finite element methods. A retrospective clinical study. Bone. 2018;110:215–220. doi:10.1016/j.bone.2018.02.011
9. Clark CR, Morgan C, Sonstegard DA, et al. The effect of biopsy-hole shape and size on bone strength. J Bone Joint Surg Am. 1977;59:213–217. doi:10.2106/00004623-197759020-00014
10. Matsuura Y, Giambini H, Ogawa Y, et al. Specimen-specific nonlinear finite element modeling to predict vertebrae fracture loads after vertebroplasty. Spine. 2014;39:E1291–E1296. doi:10.1097/BRS.0000000000000540
11. Iwai T, Hoshi M, Oebisu N, et al. Exploration of the optimal shape for bone tumour biopsy. Anticancer Res. 2019;39:4191–4197. doi:10.21873/anticanres.13579
12. Iwai T, Hoshi M, Oebisu N, et al. Risk assessment for pathological fracture after bone tumour biopsy. Anticancer Res. 2021;41:679–686. doi:10.21873/anticanres.14819
13. Les CM, Keyak JH, Stover SM, Taylor KT, Kaneps AJ. Estimation of material properties in the equine metacarpus with use of quantitative computed tomography. J Orthop Res. 1994;12:822–833. doi:10.1002/jor.1100120610
14. Keyak JH, Rossi SA, Jones KA, Les CM, Skinner HB. Prediction of fracture location in the proximal femur using finite element models. Med Eng Phys. 2001;23:657–664. doi:10.1016/s1350-4533(01)00094-7
15. Drucker DC, Prager W. Soil mechanics and plastic analysis of limit design. Q Appl Math. 1952;10:157–165. doi:10.1090/qam/48291
16. Bessho M, Ohnishi I, Matsuyama J, Matsumoto T, Imai K, Nakamura K. Prediction of strength and strain of the proximal femur by a CT-based finite element method. J Biomech. 2007;40:1745–1753. doi:10.1016/j.jbiomech.2006.08.003
17. Miura M, Nakamura J, Matsuura Y, et al. Prediction of fracture load and stiffness of the proximal femur by CT-based specimen specific finite element analysis: cadaveric validation study. BMC Musculoskelet Disord. 2017;18:53. doi:10.1186/s12891-017-1898-1
18. Kawaguchi N, Ahmed AR, Matsumoto S, et al. The concept of curative margin in surgery for bone and soft tissue sarcoma. Clin Orthop Relat Res. 2004;419:165–172. doi:10.1097/00003086-200402000-00027
19. Willeumier JJ, van der Linden YM, van de Sande MAJ, et al. Treatment of pathological fractures of the long bones. EFORT Open Rev. 2017;1:136–145. doi:10.1302/2058-5241.1.000008
20. Schlegel M, Zeumer M, Prodinger PM, et al. Impact of pathological fractures on the prognosis of primary malignant bone sarcoma in children and adults: a single-center retrospective study of 205 patients. Oncology. 2018;94:354–362. doi:10.1159/000487142
21. Zhang P, Kang L, Hu Q, et al. Treatment of diaphyseal pathological fractures in children with monostotic fibrous dysplasia using cortical strut allografts and internal plating: a retrospective clinical study. Medicine. 2019;98:e14318. doi:10.1097/MD.0000000000014318
 © 2021 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2021 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.