Back to Journals » Open Access Journal of Clinical Trials » Volume 7
On controversial statistical issues in clinical research
Received 17 January 2015
Accepted for publication 25 February 2015
Published 2 May 2015 Volume 2015:7 Pages 43—51
DOI https://doi.org/10.2147/OAJCT.S63266
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Greg Martin
Shein-Chung Chow,1 Fuyu Song2
1Duke University School of Medicine, Durham, NC, USA; 2Peking University Clinical Research Institute, Peking University Health Science Center, Beijing, People's Republic of China
Abstract: In clinical development of a test treatment under investigation, clinical trials are often conducted for evaluation of safety and efficacy of the test treatment. To provide an accurate and reliable assessment, adequate and well-controlled clinical trials using valid study designs are necessarily conducted for obtaining substantial evidence of safety and efficacy of the test treatment under investigation. In practice, however, some debatable issues are commonly encountered regardless compliance with good statistics practice and good clinical practice. These issues include, but are not limited to: 1) appropriateness of statistical hypotheses for clinical investigation; 2) correctness of power analysis assumptions; 3) integrity of randomization and blinding; 4) post hoc endpoint selection; 5) impact of protocol amendments on the characteristics of the trial population; 6) multiplicity in clinical trials; 7) missing data imputation; 8) adaptive design methods; and 9) independence of a data monitoring committee. In this article, these issues are briefly described. The impact of these issues on the evaluation of the safety and efficacy of the test treatment under investigation are discussed with examples whenever applicable. Some recommendations regarding possible resolutions of these issues are also provided.
Keywords: data safety monitoring committee, endpoint selection, integrity of blinding, missing data imputation, multiplicity, protocol amendment, two-stage adaptive designs
Introduction
In clinical research and development of a test treatment, relevant clinical data are usually collected from subjects with the diseases under study in order to evaluate safety and efficacy of the test treatment under investigation. To provide an accurate and reliable assessment, adequate well-controlled clinical trials using valid study designs are necessarily conducted for obtaining substantial evidence of the safety and efficacy of the test treatment under investigation. The clinical trial process, which consists of protocol development, trial conduct, data collection, statistical analysis/interpretation, and reporting, is a lengthy and costly process. This process is necessary to ensure a fair and reliable assessment of the test treatment under investigation. In practice, some controversial or debatable issues inevitably occur regardless the compliance to good statistics practice (GSP) and good clinical practice (GCP). Chow1 and Chow et al2 define controversial issues in clinical research as debatable issues that are commonly encountered during the conduct of clinical trials. In practice, debatable issues could be raised from: 1) compromises between theoretical and real practices; 2) miscommunication, misunderstanding, and/or interpretation in perception among regulatory agencies, clinical scientists, and biostatisticians; and 3) disagreement, inconsistency, and errors in clinical practice.
In clinical research and development of a test treatment under investigation, commonly seen controversial issues include: 1) appropriateness of traditional statistical hypotheses for clinical evaluation of both safety and efficacy; 2) correctness of power analysis for sample size calculation based on information from a small-scale pilot study; 3) integrity of randomization and blinding for preventing potential biases; 4) post hoc endpoint selection (based on some derived endpoints); 5) impact of protocol amendments on the characteristics of the trial population; 6) multiplicity in clinical trials; 7) missing data imputation; 8) adaptive design methods; and 9) independence of the data monitoring committee (DMC).
In this article, we will review these debatable issues rather than provide resolutions. The impact of these issues on the evaluation of the safety and efficacy of the test treatment under investigation is discussed with examples whenever applicable. Recommendations regarding possible resolutions of these issues are also provided whenever possible. It is our goal that medical/statistical reviewers from regulatory agencies such as the United States Food and Drug Administration (FDA), clinical scientists, and biostatisticians will: 1) pay attention to these issues; 2) identify the possible causes of these debatable issues; 3) resolve/correct the issues; and, consequently 4) enhance GSPs and GCPs for achieving the study objectives of the intended clinical trials.
Appropriate hypotheses for clinical investigation
In clinical trials, a typical approach for clinical investigation of safety and efficacy of a test treatment under investigation is to first test for the null hypothesis of no treatment difference in efficacy based on clinical data collected under a valid trial design. If significant, the investigator would reject the null hypothesis of no treatment difference and then conclude the alternative hypothesis that there is a difference in favor of the test treatment. If there is a sufficient power for correctly detecting a clinically meaningful difference (improvement) when such a difference truly exists, we claim that the test treatment is efficacious. The test treatment will then be reviewed and approved by the regulatory agency such as FDA if the test treatment is well tolerated and there appears to be no safety concerns.
In practice, however, it is a concern whether the traditional approach based on hypothesis testing on efficacy alone (ie, the study is powered based on the efficacy alone) for evaluation of both safety and efficacy of a test treatment under investigation is appropriate. The test treatment may be approved by the regulatory agency based on the hypothesis testing on efficacy alone and subsequently be withdrawn due to safety concerns. A typical example is the withdrawal of Vioxx. Vioxx is a COX-2 inhibitor drug intended for treating arthritis approved by the FDA in 1999, which was subsequently withdrawn from the market in 2004 due to the safety concern of increased risk of heart attack and stroke.
To overcome this problem, Chow suggested that both safety and efficacy should be included in a composite hypothesis for testing clinical benefit of the test treatment under investigation.1 Composite hypotheses which take into consideration both safety and efficacy for evaluation of a test treatment under investigation are summarized in Table 1. As can be seen in Table 1, suppose, as an example, that we are interested in demonstrating therapeutic equivalence in efficacy and superiority in safety. In this case, we may consider testing the null (composite) hypothesis of H0: not ES, where E denotes therapeutic equivalence in efficacy and S indicates superiority in safety. Thus, we would reject the null hypothesis in favor of the alternative hypothesis that Ha: ES. In other words, the test treatment is therapeutically equivalent to the active control agent and its safety appears to be superior to the active control agent. To test the null hypothesis of H0: not ES, appropriate statistical tests should be derived under the null hypothesis. Under the alternative hypothesis, the test statistics can then be evaluated for achieving the desired power.
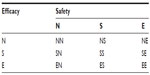  | Table 1 Composite hypotheses for clinical investigation |
It should be noted that, with a switch from single hypothesis testing (traditional approach) to a composite hypothesis testing, an increase in sample size is expected. For composite hypothesis testing, in the interest of controlling the overall type I error rate at the α level, appropriate α levels (say α1 for efficacy and α2 for safety) may be chosen.
Instability of sample size calculation
In clinical trials, power analysis for sample size calculation is necessarily performed to ensure that there is high probability of correctly detecting a clinically meaningful effect size if such an effect size truly exists. In practice, power calculation is often performed based on either: 1) information obtained from previous studies or pilot studies; or 2) pure guesses or beliefs based on the best knowledge of the investigator (with or without scientific justification). Since a pilot study is usually a small-scale study with a limited number of subjects, the data obtained from the pilot study and/or the investigator’s guess or belief could deviate far from the truth, which will bias the power calculation for sample size determination. Thus, it is a concern whether the sample size calculation based on the information from the pilot study or the investigator’s guess or belief is robust or stable.
Chow et al3 considered assessing the instability of power calculation for sample size in terms of its bias. For simplicity and illustrative purposes, consider the simple case for testing equality of treatment effect where the primary endpoint is a continuous normal variable. In other words, consider testing the following null hypothesis:
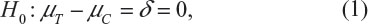
where μT and μC are the means for a test treatment and a (placebo) control, respectively, and δ is a clinically meaningful difference or effect size. Power calculation leads to the following formula for sample size calculation (see also Chow et al3):
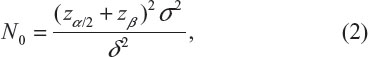
where α and β are the probabilities of committing type I error and type II error, respectively, and σ is the standard deviation of the control. In practice, δ and σ2 are often estimated by difference in sample mean 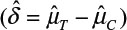 and sample variance (s2). In other words, σ2/δ2 is estimated by
and sample variance (s2). In other words, σ2/δ2 is estimated by 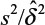 . It can be verified that the asymptotic bias leading term of
. It can be verified that the asymptotic bias leading term of 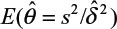 is given by (Lee et al, unpublished data, 2008):
is given by (Lee et al, unpublished data, 2008):
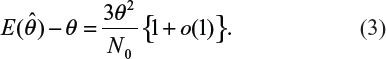
Table 2 provides biases of 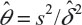 in sample size calculation with various combinations of δ, σ, and θ. As can be seen from Table 2, the sample size calculation based on estimates from a small pilot study could vary and consequently instable, especially when there is a large variability associated with the observed data. Thus, it is a concern that the estimate of effect size and standard deviation based on a pilot study is often imprecise.
in sample size calculation with various combinations of δ, σ, and θ. As can be seen from Table 2, the sample size calculation based on estimates from a small pilot study could vary and consequently instable, especially when there is a large variability associated with the observed data. Thus, it is a concern that the estimate of effect size and standard deviation based on a pilot study is often imprecise.
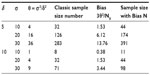  | Table 2 Biases of sample sizes |
The above discussion justifies the need for sample size re-estimation or sample size adjustment during the conduct of clinical trials. Sample size re-estimation is often planned in clinical trials utilizing group sequential design with planned interim analyses. In practice, the following sample size adjustment based on the ratio of the initial estimated effect size (E0) to the observed effect size (E) is usually considered:4
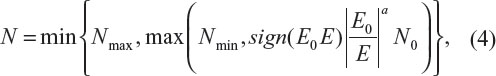
where N is the sample size after adjustment, Nmax and Nmin are the maximum (due to financial and/or other constraints) and minimum (the sample size for the interim analysis) sample sizes, respectively, a is a constant (which is usually determined based on the review of the interim analysis results), and sign(x) =1 for x>0; otherwise, sign(x) =−1. Note that the above sample size adjustment reduces to the method proposed by FDA statisticians for normal study endpoint with a=2.4
However, it should be noted that the information obtained for sample size re-estimation at the interim is still an estimate of treatment effect. Thus, the instability issue regarding sample size remains unsolved because there is a variability associated with the observed (estimated) treatment effect at the interim.
Integrity of randomization/blinding
In clinical trials, randomization and blinding (eg, double-blind) are often employed to prevent or minimize bias (eg, operational bias) from assessment of a test treatment under investigation. In randomized and double-blind clinical trials, due to human nature, both patients and the investigator may guess what treatment patients are receiving. Karlowski et al challenged the integrity of the use of randomization and blinding in a randomized, double-blind, placebo-controlled study conducted by the National Institutes of Health (NIH). The study was to evaluate the difference between the prophylactic and therapeutic effects of ascorbic acid for the common cold.5 After the completion of the study, a questionnaire regarding the knowledge of the treatment assignment was distributed to every subject enrolled in the study (a total of 190 subjects completed the study). Results from the 190 subjects are summarized Table 3.
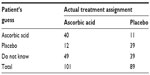  | Table 3 Results of patients’ guesses |
Table 3 indicates that there is a high percentage of patients who correctly guessed the treatment assignment they received. Thus, there is a reasonable doubt that the blindness may not be preserved during the study. Thus, “How to test for the integrity of blinding in clinical trials?” is an interesting question.
To address this question, according to Table 3, Chow and Shao proposed a test for testing the integrity of blinding.6 Without loss of generality, consider a parallel design comparing a≥2 treatments conducted at a single study site. Let Aij be the event in which a patient in the jth treatment group guesses that he/she is in the ith group, and i = 1, … a, a + 1, where i = a + 1 defines the event that a patient whose answer is “do not know” or “does not guess”. Consider the following null hypothesis:
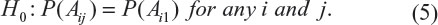
If the above null hypothesis holds, then we claim that the blindness is preserved. Chow and Shao indicated that H0 can be tested using the Pearson’s chi-squared test under the contingency tables constructed based on observed counts given in Table 3.6 As a result, a simple calculation gives Pearson’s chi-squared statistic of 31.3. Thus, the null hypothesis of independence is rejected (P-value <0.001). Thus, we conclude that the blindness is not preserved and the integrity of blinding is in doubt.
When the integrity of blinding is doubtful, it is suggested that appropriate adjustment to statistical analysis should be made.6 In practice, one of the debatable issues is that of whether a formal statistical test for the integrity of the blinding should be performed at the end of the clinical trial regardless of whether the results are positive or negative. If the results are positive, the sponsor would prefer not to perform the test. However, if the results are negative, the sponsor would argue to perform the test and hopefully to rescue the failed trial. In addition, what action should be taken if a positive clinical trial fails to pass the test for the integrity of the blinding?
Clinical strategy for endpoint selection
In clinical trials, it is not uncommon to see that we may reach some clinical endpoints but fail to achieve other clinical endpoints. In this case, the selection of clinical endpoint plays an important role for achieving the study objectives with a desired power at a prespecified level of significance. For a given primary clinical endpoint, power calculation and statistical analysis are usually performed based on either absolute change from baseline or relative (or percent) change from baseline. The absolute change from baseline and the relative change from baseline are referred to as derived study endpoints. Based on the original data obtained from the same target patient population, another derived endpoint based on the percentage of patients who show some improvement is often considered. A subject who shows some improvement is considered a responder. The definition of a responder, however, could be based on either absolute change from baseline or relative change from baseline of the primary study endpoint.
It should be noted that statistical analysis/interpretation, sample size calculation, and power for different derived study endpoints are different. Thus, endpoint selection has become very controversial, especially when a significant result is observed based on a derived endpoint but not on the other derived endpoint. For example, in weight reduction studies with obese patient populations, statistical analysis based on absolute change from baseline is often different from that based on relative (percent) change from baseline. Besides, power analysis for sample size calculation based on absolute change and relative changes could be very different depending upon what difference is considered of clinical importance. For example, the sample size required in order to achieve the desired power based on the absolute change could be very different from that obtained based on the percent change, or the percentage of patients who show an improvement based on the absolute change or relative change at α level of significance.1,2
The issue could become more complicated if the intended trial is a noninferiority trial for establishing noninferiority of a test treatment to an active control agent. In this case, sample size calculation will also depend upon the selection of noninferiority margin. Similar to endpoint selection based on either absolute change or relative change, noninferiority margin could be selected based on either absolute change or relative change. As a result, there are eight possible clinical strategies with different combinations of derived study endpoints (ie, absolute change, relative change, responder analysis with absolute change, and responder analysis with relative change) and noninferiority margins (absolute change and relative change) for assessment of the treatment effect (Table 4). To ensure the success of the intended clinical trial, a sponsor will usually carefully evaluate the eight clinical strategies through extensive clinical trial simulation for selecting the most appropriate (derived) endpoint, clinically meaningful difference, and noninferiority margin during the planning stage of protocol development.
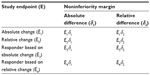  | Table 4 Clinical strategy for endpoint selection in noninferiority trial |
In practice, some clinical strategies may be successful in achieving study objectives with desired power, while some strategies may not. These inconsistent results are debatable. The sponsor may choose the strategy to their best interest, while the FDA may challenge the sponsor regarding the inconsistent results. In other words, the FDA may ask the sponsor to address the questions of: 1) which endpoint is telling the truth; and 2) can these study endpoints translate one another since they are derived based on data collected from the same patient population?
Impact and sensitivity of protocol amendments
In clinical trials, protocol amendments are commonly issued after the initiation of a clinical trial due to various reasons such as slow enrollment and/or safety concerns. In practice, before a protocol amendment can be issued, a detailed description, rationales, and clinical/statistical justification regarding the changes must be provided to ensure the validity and integrity of the clinical trial. Statistically, it is often a concern that major or significant changes or modifications to study protocol could result in a similar but different patient population. For example, if major or significant changes are made to eligibility (inclusion/exclusion) criteria of the study, the original target patient population may have become a similar but different patient population. This raises the debatable issue regarding the validity and reliability of the statistical inference to be drawn based on data collected before and after protocol amendment.
To evaluate whether major or significant changes made to the original target patient population has resulted in a similar but different target patient population after protocol amendments, let (μ, σ) denote the original target patient population. Also, denote by (μ1, σ1) the resultant (actual) patient population after the implementation of a protocol amendment, where μ1=μ+ε and σ1=Cσ(C>0). The shift in treatment effect of the original target patient population can be characterized by:
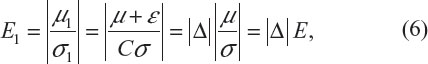
where Δ = (1 + ε/μ)/C; E and E1 are the effect size before and after population shift, respectively; and Δ is a sensitivity index measuring the change in effect size between the original target patient population and the actual patient population (see, for example, Chow et al and Chow and Shao7,8). Table 5 provides an evaluation of the impact of protocol amendment in terms of sensitivity index under various scenarios of location shift (ie, change in ε) and scale shift (ie, change in C). As can be seen from Table 5, with the shifts in ε and C (inflation or deflation), the sensitivity index Δ varies from 0.667 to 1.500. It should also be noted that the shift in ε could be offset by the shift in C.
  | Table 5 Evaluation of sensitivity index |
If there is evidence that the mean response is correlated to some covariates, Chow et al9 proposed an alternative approach by considering a model that links the population means and the covariates. In many cases, however, such covariates may not be observable or may not even exist. In this case, Chow et al’s approach is not applicable. Alternatively, it is suggested that the sensitivity index Δ be assessed by assuming that there are random shifts in both location or scale parameters.10
In practice, it is not uncommon to have a number of protocol amendments after the initiation of a clinical trial. Frequent issuance of protocol amendments may result in a shift in target patient population. Thus, regulatory guidances or regulations on 1) levels of changes, and 2) number of protocol amendments that are allowed are necessarily developed for maintaining the validity and integrity of the intended study.
Controversial issue of multiplicity in clinical trials
In clinical trials, multiplicity is usually referred to as multiple inferences that are made simultaneously.11 The concept of multiplicity could include comparison of: 1) multiple doses (treatments); 2) multiple endpoints; 3) multiple time points; 4) multiple interim analyses; 5) multiple tests of the sample hypothesis; 6) variable/model selection; and 7) subgroup analyses. In practice, it is of interest to the investigators when adjustment for multiplicity should be performed for controlling the overall type I error rate at a prespecified level of significance.
To address this issue, the International Conference on Harmonization (ICH) published a guideline on statistical principles in clinical trials in 1998.12 This guideline indicates the concern regarding the multiplicity issue for providing substantial evidence in clinical trials. The ICH guideline suggests that data analysis of the clinical trial may necessarily adjust for controlling the overall type I error rate. Moreover, the guideline requires that any adjustment procedure or an explanation (justification) regarding why adjustment is not done should be described in detail in the statistical analysis plan.12 Similarly, the issue of multiplicity is also addressed in the European Agency for the Evaluation of Medicinal Products (EMEA).13 In 2007, the Committee for Proprietary Medicinal Products published a draft guidance Points to Consider on Multiplicity Issues in Clinical Trials.14 This guideline points out that multiplicity can have a substantial influence on false positive rate when there is an opportunity to select the most favorable results from two or more analyses. Both the EMEA guideline and the ICH guideline recommend stating details of the multiple comparisons procedure in the statistical analysis plan.
In their review article, Westfall and Bretz indicated that the following are the most commonly seen controversial issues regarding multiplicity in clinical trials:11
- Penalizing for doing more.
- Adjusting α for all possible tests in the trial.
- Testing for family of hypotheses.
Penalizing for doing a good job is referred to as adjustment for multiplicity in dose-finding trials which often involve several dose groups. For adjusting α for all possible tests, it is excessive to control the α at the prespecified level because it is not the study objective to show that all of the observed differences (simultaneously) are not by chance alone. In clinical trials, it is debatable for choosing an appropriate family of hypotheses (eg, primary and secondary study endpoints) and adjust α for multiple comparisons for clinical investigation of the test treatment under study.
Although ICH12 and EMEA13 did provide some guidances for adjustment of multiplicity, regulations regarding multiplicity adjustment are still not clear. Marcus et al indicated that there is no need for multiplicity adjustment for closed testing procedure.15 Chow pointed out that one should always look the primary null hypothesis before deciding whether there is a need for multiplicity adjustment.1
Validity and power of missing data imputation
Missing data inevitably occurs in clinical trials. When there are a few missing values, one of the approaches is to impute the missing values with their estimates under some valid and appropriate statistical models. Missing data imputation then becomes one of the most debatable issues in clinical trials. The following questions are often asked when there are missing values in clinical trials:
- Why impute missing values?
- What methods should be used if we are to impute the missing values?
- What if there are a high percentage of missing values?
For the first question, some clinical scientists criticize that missing data imputation actually makes up the data we do not observe. We should not make up data for missing data as missing data imputation could bias the assessment of treatment effect and hence missing data imputation does not add much value to the clinical research. For the second question, the method of last observation carry forward (LOCF) is widely used although it has been recognized that the validity of LOCF is questionable. In addition to the method of LOCF, other methods such as the mixed effects model for repeated measures, generalized estimating equations, and complete-case analysis of covariance are often employed in missing data imputation. When there is large proportion of missing values, it is suggested that missing data imputation should not be applied. This, however, raises a debatable issue for determination of the cut-off value for the proportion of missing values for preserving good statistical properties of the statistical inference derived based on the incomplete data set and imputed (complete) data set.
Statistically, one of the concerns for missing data imputation is the potential reduction of power. In clinical trials, it is recognized that missing data imputation may inflate variability due to additional variability associated with the imputed missing data. The inflation of variability will definitely decrease the power. Consequently, the intended clinical trial will not be able to address the scientific/clinical questions asked with desired power. This could be a major concern for regulatory review and approval.
To address current issues and recent development of missing data imputation, the Journal of Biopharmaceutical Statistics published a special issue on missing data prevention and analysis in 2009.16 Soon indicated that management of missing data involves missing data prevention and missing data analysis, which are equally important in the handling of missing data.16 Missing data prevention can be achieved through the enforcement of GSPs and GCPs during the clinical trial process, including clinical operations personnel training for data collection. It should be noted that despite the effort, missing data cannot be totally avoided, and may occur due to factors beyond the control of patients, investigators, and clinical project teams.
Flexibility and feasibility of two-stage adaptive design
A seamless trial design is a study design that can address study objectives within a single trial which are normally achieved through the conduct of separate independent trials. A seamless adaptive design is a seamless trial design that fully utilizes data collected from patients before and after the adaptation in the final analysis. A seamless trial design is called a two-stage seamless design if it combines two studies into a single study. Thus, a two-stage (seamless) adaptive design consists of two phases (stages; each stage contains one study), namely, learning or exploratory phase and confirmatory phase. A two-stage seamless adaptive trial design reduces lead time between studies (ie, the first study and the second study). Most importantly, data collected at the learning phase are combined with those data obtained at the confirmatory phase for final analysis.
For a two-stage adaptive design, since it combines two independent trials into a single study, the study objectives and study endpoints at different stages (studies) could be different. Depending upon study objectives and endpoints used, two-stage adaptive trial designs can be classified into four categories of designs as indicated in Table 6.
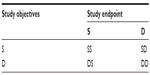  | Table 6 Classifications of two-stage adaptive designs |
Thus, we have SS (same objectives and same endpoints), SD (same objectives and different endpoints), DS (different objectives and same endpoints), and DD designs, where SS designs indicate study designs with the same objectives and same endpoints at different stages and so on. In clinical trials, different study objectives could be dose finding or treatment selection at the first stage and efficacy confirmation at the second stage. Different study endpoints could include biomarker, surrogate endpoint, and clinical endpoint with different (shorter) treatment duration at the first stage versus clinical endpoint at the second stage, or the same clinical endpoint with different treatment durations.
SS designs are similar to typical group sequential designs with one planned interim analysis. Thus, standard methods for a typical group sequential design can be directly applied to the SS designs.
In this article, our emphasis will be placed on SD, DS, and DD designs. In practice, typical examples for SD, DS, and DD designs include a two-stage Phase I/II adaptive design, which is often employed in early clinical development, and a two-stage Phase II/III adaptive design, which is usually considered in late phase of clinical development. For example, for the two-stage Phase I/II adaptive design, the objective at the first stage is for biomarker development and the study objective at the second stage is to establish early efficacy. For a two-stage Phase II/III adaptive design, the study objective at the first stage could be for treatment selection while the study objective at the second stage could be for efficacy confirmation.
One of the most debatable issues regarding the flexibility and feasibility of the use of two-stage adaptive design in early phase and/or late phase of clinical development is the efficiency and effectiveness of the trial design as compared to the traditional approach (ie, conducting two separate trials). To address this issue, Table 7 provides a simple comparison in terms of significance level, power, lead time, and sample size required for achieving a desired power.
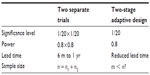  | Table 7 Simple comparison |
As can be seen from Table 7, a traditional approach by conducting two separate trials does provide substantial evidence at 1/400 level of significance level with a 64% power, while the two-stage adaptive design will achieve an 80% power at the 5% (1/20) level of significance. Besides, the use of two-stage adaptive design could reduce lead time between studies and hence shorten the process of clinical development. In terms of the sample size required, the use of two-stage adaptive design may also reduce the sample size required for achieving the desired power depending upon the study objectives and the study endpoints used at different stages in the two-stage adaptive trial design. Note that sample size calculation and statistical analysis for SD, DS, and DD designs can be found in Chow and Chang.10
When applying a two-stage adaptive design in clinical trials, one of the most challenging and debatable questions often asked by the regulatory agency such as the FDA is related to the concern that the overall type I error rate may not be controlled at a prespecified level of significance when 1) O’Brien–Fleming type boundaries (such as Lan–DeMets boundary) and 2) additional adaptations are applied.
Challenge of the independence of DMCs
In clinical trials, a DMC is usually established to monitor the validity and integrity of the intended clinical trial. The DMC is independent from the project team, which performs ongoing safety monitoring and/or interim analyses for efficacy. Typically, a DMC consists of experienced physicians and biostatisticians. A charter is necessarily developed to outline the activities and functions of the DMC, but also to describe roles and responsibilities of DMC members.
One of the major concerns regarding an established DMC is the independence of the DMC. A DMC has the authority to perform a review of unblinded data, though most DMCs prefer a blinded review of interim data. After the review of interim data, a DMC has the authority to stop the trial early due to safety, futility, and/or efficacy. In clinical trials, an independent DMC ensures the quality, validity, and integrity of the clinical trial. Some sponsors, however, will make every attempt to influence the function and activity of the DMC, which challenges the independence of the DMC. The following is a summary of some observations which are commonly seen in DMCs across various therapeutic areas:
- DMC members are selected and appointed by the sponsors.
- The DMC charter is usually developed by the sponsor. The charter is developed without consulting with the DMC members. DMC members usually do not have the chance to review it until the organizational meeting. As result, the charter is usually approved in a hurry.
- The trial may have begun to enroll patients prior to the DMC organizational meeting.
- Those DMC members who have disagreements with the sponsor are replaced prior to the DMC meeting. To avoid selection bias, it is suggested that the reasons for replacing DMC members be documented.
- DMC members and investigators are from the same organization with administrative reporting relationships.
- There is no single voice from the DMC.
- The sponsor issues protocol amendments or modifies randomization schedules without consulting with DMC members.
- The project statistician and the unblinded (or DMC support) statistician are the same person.
Based on the above observations, it is doubtful that an independent DMC is really independent. In addition, the following debatable issues have also been raised. First, should the DMC directly communicate with regulatory agencies for any wrongdoing in the conduct of the intended clinical trial? Second, can the DMC perform well if a less-well-understood adaptive design is used in the intended clinical trial?
Conclusion
In this article, several commonly encountered statistical controversial issues in clinical research are discussed. In practice, many more debatable issues are still under tremendous discussion among regulatory agencies, academia, and the pharmaceutical industry. These debatable issues include the issue of placebo effect, the impact of baseline adjustment, selection of noninferiority margin in active control trials, the use of Bayesian methods in clinical research, issues in bridging and/or multinational (multiregional) studies, and the potential misuse and abuse of adaptive trial designs (especially those less-well-understood design as described in the FDA draft guidance on adaptive trial design). Most recently, the scientific/statistical issues on the assessment of biosimilarity and interchangeability of biosimilar drug products have received much attention. These issues such as “How similar is considered highly similar?” and “A biosimilar product is expected to produce the same clinical result in any given patient” are debatable from different perspectives of regulatory agencies, academia, and the pharmaceutical/biotech industry.
It should be noted that, debatable issues are likely encountered in clinical trials. Consequently, the accuracy and reliability of statistical inference on the treatment effect is a concern to the investigator. To address this issue, Shao and Chow17 and Chow and Shao18 proposed the concept of reproducibility and generalizability of evaluation of the accuracy and reliability of the clinical trials. The reproducibility is defined as the probability of observing positive results (which have achieved statistical significance) of future clinical trials that are conducted under similar experimental conditions given the observed significant positive clinical results. Shao and Chow17 suggested considering the probability of reproducibility as a monitoring tool for the performance of a test treatment under investigation for regulatory approval. The evaluation of reproducibility provides valuable information which protects patients from unexpected risk of the test treatment. For example, in a given clinical trial with a relatively low probability of reproducibility, the observed significant positive clinical results may not be reproducible if the clinical trial is repeatedly conducted under similar experimental conditions. To ensure that there is a high reproducibility (say 95%), Chow and Shao18 indicated that the P-value for the observed positive results should be less than 0.001 (ie, the study has to be highly significant).
Disclosure
The authors report no conflicts of interest in this work.
References
Chow SC. Controversial Issues in Clinical Trials. New York: Chapman and Hall/CRC Press, Taylor & Francis; 2011. | |
Chow SC, Yang LY, and Lu Y. Some controversial issues in clinical trials. Ther Innov Regul Sci. 2011;45:163–174. | |
Chow SC, Shao J and Wang H. Sample Size Calculation in Clinical Research. 2nd ed. Taylor and Francis; 2007. | |
Cui L, Hung HM, Wang SJ. Modification of sample size in group sequential trials. Biometrics. 1999;55:853–857. | |
Karlowski TR, Chalmers TC, Frenkel LD, Kapikian AZ, Lewis TL, Lynch JM. Ascorbic acid for the common cold: a prophylactic and therapeutic trial. JAMA. 1975;231:1038–1042. | |
Chow SC, Shao J. Analysis of clinical data with breached blindness. Stat Med. 2004;23:1185–1193. | |
Chow SC, Shao J, Hu OY. Assessing sensitivity and similarity in bridging studies. J Biopharm Stat. 2002;12:385–400. | |
Chow SC, Shao J. Inference for clinical trials with some protocol amendments. J Biopharm Stat. 2005;15:659–666. | |
Chow SC, Chang M, Pong A. Statistical consideration of adaptive methods in clinical development. J Biopharm Stat. 2005;15:575–591. | |
Chow SC, Chang M. Adaptive Design Methods in Clinical Trials. 2nd ed. New York: Chapman and Hall/CRC Press, Taylor and Francis; 2011. | |
Westfall P, Bretz F. Multiplicity in clinical trials. In: Chow SC, editor. Encyclopedia of Biopharmaceutical Statistics. 3rd ed. New York: Taylor and Francis; 2010:889–896. | |
ICH. ICH Harmonized Triplicate Guideline: Statistical Principles for Clinical Trials E9. Geneva: ICH; 1998. | |
EMEA. Reflection Paper on Methodological Issues in Confirmatory Clinical Trials Planned with an Adaptive Design. London: European Medicines Agency; 2007. Available from: http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003616.pdf. | |
EMEA. Points to consider on multiplicity issues in clinical trials. London: The European Agency for the evolution of medicinal products evaluation of medicines for human use; 2002. Available from: http://www.ema.europa.eu/docs/en_EG/document_library/scientific_ guideline/2009/09/wc500003640.pdf | |
Marcus R, Peritz E, Gabriel KB. On closed testing procedures with special reference to ordered analysis of variance. Biometrika. 1976;63:655–660. | |
Soon G. Editorial: missing data – prevention and analysis. J Biopharm Stat. 2009;19(6):941–944. | |
Shao J, Chow SC. Reproducibility probability in clinical trials. Stat Med. 2002;21:1727–1742. | |
Chow SC, Shao J. Statistics in Drug Research. New York: Marcel Dekker, Inc.; 2002. |
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
