Finite Element Analysis of Restored Principal Abutment in Free-End Saddle Partial Denture

Introduction

Removable partial dentures (RPDs) are used to restore oral function, preserve remaining oral structures, and prevent oral disease as much as possible.¹ They are constructed to meet the functional, preventative, and aesthetic demands placed on them. As a rule, advancing axial load is achieved by preparing occlusal rest seats on the supporting, confirmable surfaces of the abutment teeth.² Cutting the enamel to achieve depressions of the proper proportions is required for occlusal rest-seat layout.³ Furthermore, appropriate retention is the most significant factor affecting the clinical success of removable partial dentures (RPDs) especially patients suffering from bilateral missing posterior teeth as Kennedy Class I removable partial dentures, which are considered very special and thought-provoking situation.⁴ In a clinical environment, wear of the enamel or composite resin in comparison to the direct retainer is unlikely to produce a significant loss of retention.^5,6 In restorative, endodontic, and implant dentistry, finite element analysis (FEA) has been utilized to calculate novel mechanical and structural aspects of the material’s behavior. It is based on mathematical and numerical analyses, and it can effectively illustrate the stress distribution pattern by analyzing finite small elements, the behavior of which can be summarized and calculated. Furthermore, it can easily determine the stress magnitude and distribution, as well as the influence of various materials which cannot be determined using traditional in vitro tests.⁷ It has proven to be a useful way to understand tooth biomechanics and the biomimetic approach in restorative dentistry.⁸ The filler framework has been adjusted in commercial composites in recent years, and the size of the filler particles integrated into the resin matrix of industrial composites has continuously decreased, resulting in enhanced material properties for nanohybrid and nanofilled materials.⁹ This research analyzed the stress distribution on restored principal abutments in free-end saddle partial denture and the null hypothesis of this study was that there would be no difference in von Mises stress in class II cavities restored with nanohybrid composite resins with occlusal rest seat.

Materials and Methods

Finite element analysis (FEA) is a numerical process for studying structures that involves stressing and analyzing a computer model of a material or design for specified outcomes. It employs a complicated system of points (nodes) and elements to create a grid called a mesh.¹⁰ Three digital models were created for finite element analysis (FEA) as follows: Model 1: non-restored control model, Model 2 restored with Tetric N-Ceram composite resin, and Model 3 restored with Charisma Smile composite resin. Class II composite resin restoration with 2-mm depth and 1.5-mm, width and an appropriate occlusal rest seat preparation with 1.5-mm depth in a mandibular single-root premolar was conducted using software (Rapidform XOR and Solidwork 2012). The recommended dimensions and the material properties for the components used in this study were adopted from recommendations in literature.^8,11–13 Elastic constant E (Young’s modulus of elasticity) describes the relative stiffness or rigidity of the material within the elastic range. It was determined from the stress-strain graph, as it represented the ratio of the elastic stress to the elastic strain. Poisson’s ratio is the ratio of the lateral strain to the axial strain within the elastic range.¹⁰ Due to the complex geometrical characteristics of the tooth, thinner sections/slices of the tooth were obtained. In the Modeling section, a file format called STL (Stereolithography) file of a mandibular premolar was introduced into rapid form software.¹⁴ Figure 1; The material types were added to the Assignment section and all connections between all faces were bounded. Later, a mesh was created in the Mesh section. Creation of a body mesh is one of the most important steps in finite element analysis (FEA) and it constitutes its core. There are nodes and elements in the mesh. Figure 2; The connection between multiple nodes creates the elements. More nodes imply an accurate solution. The final step was to identify the boundaries. In this research, we had frictionless support to obtain an accurate solution. A load of 200-N was applied vertically and obliquely to the cusp fossa and buccal inclines respectively to simulate the masticatory forces.¹⁵ The occlusal contact points were defined at the tips of the cusps using a stainless-steel spherical loading device model. The von Mises criteria were used to observe the coherence of the numerical simulations. The maximum principal stress criteria were chosen to evaluate the tensile stress results.¹³ All materials were considered homogeneous, linear, and isotropic, and their mechanical properties are summarized in Table 1.^8,11–13

Table 1 Material Properties Were Assigned to Dental Tissues and Restorative Materials

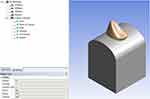Figure 1 Tooth simulation into rapid form software.

Figure 2 Finite element model mesh.

Results

Based on the assumptions involved in the study and the fact that computer simulations simplified the real problems, the results of the study might be different from the values of the stresses encountered by teeth in real situations. Therefore, the results were presented and considered qualitatively, not quantitively, to offer more insight into the general influence of the prosthetic devices placed on teeth.² The modified von Mises shrinkage stress distributions at the occlusal surface for the different restorative materials are shown in Figures 3 and 4. Stresses in (MPa= 10⁶ Pa) were calculated and presented as a linear color scale; different colors represent different levels, in which blue indicates the lowest stress values and yellow and light grey represent the highest stress values. In general, the composite resin factor and cavity geometry affected the stress distribution in the tooth. When the models were evaluated according to restoration type, no significant difference was observed between the types of composite resins (Tetric N Ceram and Charisma Smile) used and rest seat preparation. Differences were observed between models to which vertical forces were applied and those to which oblique forces were applied. Figure 5.

Figure 3 Finite element analysis of Tetric N Ceram composite resin.

Figure 4 Finite element analysis of Charisma Smile composite resin.

Figure 5 A column chart of maximum von Mises stresses (vertical and oblique) for the control group and restorative materials.

Discussion

The null hypothesis of this study was that there would be no difference in von Mises stresses in class II cavities restored with nanohybrid composite resins with occlusal rest seat and the results showed that different composite resin restorations with a rest seat included did not affect the stresses inside the tooth structure. Thus, the hypothesis was accepted given that no significant difference was found in von Mises stresses in class II cavities was restored with nanohybrid composite resins with occlusal rest seat. A class II cavity model restored with nanohybrid composite resin was used because composite resin is currently the first option for restorative materials due to its ability to mimic missing dental tissues, easy handling, proper adhesion, adequate mechanical resistance, and mechanical behavior of enamel and dentin.¹⁵

In addition, nanohybrid composite resins contain 0.005 to 0.01-nm particles and provide good aesthetic as well as satisfactory physical, chemical, and biological properties which are deemed necessary for increased longevity of the restoration.¹⁶ The long-term success of composite restorations is dependent on the resistance of different components of this complex system such as different surfaces and interfaces, to stress and deformation.¹⁷ Incorrect stress distribution in restorations can add to the stress caused by polymerization shrinkage, so, finite element analysis (FEA) was used to quantify the biomechanical behaviors of complex structures.¹⁸ “Model idealization” and “model standardization” were two terms that came up during the construction of the geometrical model represented in the study cases. The term “model idealization” refers to how closely the simulation resembles a clinical situation. As a result, the results become more reliable and appropriate for clinical cases. Regarding the current investigation, to obtain such idealization, the tooth solid model and dimensions of the premolar were derived from the average dimensions described in the literature on tooth morphology and were applied in this study. On the other hand, for model standardization, only one model of the premolar was constructed, and copies were made.¹⁹ For modeling, many methodologies have been utilized, including 3D surface scanning of an actual premolar. Others employed three-dimensional CT scanning. Both techniques require complicated procedures for modeling the teeth and transferring the created 3D models to a computer format that the finite element analysis application can manage. Because the shape and dimensions of the premolar remained fixed in all situations, such sophistication was not needed for our investigation.²⁰ Furthermore, adequate values for modulus of elasticity were chosen for dental tissues such as enamel and dentin, as well as restorative materials to establish standardization.²¹ The load applied in a finite element analysis might be static or dynamic. Due to software and hardware restrictions, the dynamic load could not be reproduced in this study. The following parameters were used to apply static loads: 200-N was chosen as the occlusal loading magnitude (simulating masticatory forces applied on a mandibular premolar). The central fossa of the restoration was subjected to vertical load.¹⁸ Loads of up to 300 N can be safely applied without tooth fracturing according to Jantarat et al.²² For the analysis, the stress conditions were represented using von Mises equivalent stresses. The advantage of employing comparable von Mises stresses is that it simplifies the interpretation of the overall stress state by combining a multidimensional stress distribution (six Cartesian stress components or three principal stresses) into a single value. The equivalent stress used is based on the well-known Von Misses formula, which has been modified to account for the differential compressive and tensile strengths of enamel, dentin, and the composite.^23,24 The occlusal contact areas showed the greatest stress in Model 1. In Models 2 and 3, due to the small difference in the modulus of elasticity of the two composite systems (Tetric N Ceram and Charisma Smile), the stress distribution and maximum stress obtained were similar. Occlusal contact areas also had the greatest von Mises stress values of restored teeth. The difference in elasticity modulus or the fact that the applied force is concentrated on the enamel in the occlusal contact areas could explain the higher von Mises stress values seen in enamel compared to the restorative material of repaired teeth. Because the structural continuity of the tooth is mechanically different when the elasticity modulus of dentin and restorative material differs, larger stresses will arise.¹² Another investigation observed no significant differences in stress distribution for composite resins with similar moduli of elasticity.²⁵ This might be related to the cavity size and configuration, which affect the degree of tooth deformation induced by resin polymerization shrinkage. In a small restoration (Class I and small Class II), deformation could hardly be seen, indicating that it was consistently lower or close to the measurement resolution.²⁶ The cavity designed for the rest seat in this study was of smaller dimensions than that of the conventional class II restoration, we may assume that the observed deformation was caused by the applied loading of the occlusal rest and not partly due to resin polymerization shrinkage.² Lin et al,²⁷ confirmed this by discovering that preparation design has a significant impact on the stress value (>80%). Furthermore, Matuda et al,¹³ concluded that conservative class II preparations should be performed to reduce the volume of resin composite material, and the stress of the direct proximal restorations. Kantardzic et al,²⁸ found that cavity design preparation affects von Mises stress values in premolars restored with direct resin composite. Borges et al,²⁹ also found that the C factor, the quantity of restorative material utilized, and the cavity geometry all have different effects on stress distribution. This finding, on the other hand, contradicted those of previous research which claimed that the presence of an occlusal rest seat in an occlusal restoration weakens the tooth structure and increases stress, with depth being more important than width.^30–32 The present investigation considered restorations in a theoretical model to reproduce the real situation as much as possible.⁶ However, various limitations should be considered when interpreting the results, PH variation simulation, cyclic loading, restoration adhesive failure, biofilm formation, temperature variation, and different antagonists. Furthermore, the results were not calculated considering data deviation or systematic error which can be present in biological tissues and complex systems.¹³ Despite limitations, the present study assists clinicians in selecting the appropriate composite resin when an improved mechanical response is needed.⁶

Conclusion

Within the limitations of this study, the results suggest that Tetric N Ceram and Charisma Smile restorations with a rest seat included did not affect the stresses in principal abutment in free-end saddle partial denture. The nanohybrid composite resin absorbs the loading and its resilient nature acts as a cushion beneath the occlusal rest. However clinical trials are required to ensure that a composite resin restoration with rest seat can survive under long-term clinical conditions.

Clinical Significance

Nanohybrid composite resin restorations may be suggested as a way of preparing abutments for receiving elements of the removable partial denture (RPD).