Back to Journals » Vascular Health and Risk Management » Volume 15
Evaluation of the calculation formulas of the cardio-ankle vascular index used in the Japanese apparatus
Authors Ato D
Received 14 May 2019
Accepted for publication 1 September 2019
Published 13 September 2019 Volume 2019:15 Pages 395—398
DOI https://doi.org/10.2147/VHRM.S215709
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Dr Daniel Duprez
Dai Ato
Gakujutsu Shien Co., Ltd., Tokyo, Japan
Correspondence: Dai Ato
Gakujutsu Shien (Academic Support) Co., Ltd., 2-1-17 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
Tel +81 3 6869 6438
Email [email protected]
Background: Recently, coefficients in the equation of cardio-ankle vascular index (CAVI) used in VaSera® device were disclosed. This study aimed to simulate the influence of adjusting the coefficients in the equation of CAVI and also aimed to validate the equation.
Methods: The CAVI displayed by VaSera (CAVIvs) and the CAVI estimated (CAVIes) with fixing the coefficients of the middle range of the heart-ankle stiffness parameter β (haβ) in the equation were compared. Moreover, the heart-ankle pulse wave velocity (haPWV) which corresponds to the low cutoff haβ of 7.348 was estimated in various blood pressure patterns to validate the formula.
Results: The CAVIvs was clearly lower than CAVIes in the low and the high range of CAVIvs. Moreover, it was virtually impossible to obtain the low cutoff haβ of 7.348 by using typical values of haPWV.
Conclusion: The CAVIvs in the high-range of VaSera underestimates the original property of stiffness parameter β. Moreover, there will be also a missing information in the equations introduced in the corresponding article, especially in the calculation formula of CAVIvs from haβ. Therefore, in order to make the best use of the nature of the stiffness parameter β to be used in VaSera, fixing the coefficients or termination of its use should be considered.
Keywords: brachial-ankle pulse wave velocity, arterial stiffness, arterial compliance, vascular function, peripheral arterial disease, ankle-brachial index
In a recent article published in the Journal of Atherosclerosis and Thrombosis, Takahashi et al disclosed the values of coefficients “a” and “b”, which are used to calculate the cardio-ankle vascular index (CAVI) using the VaSera® (VS) device.1 CAVI estimated using VS (CAVIvs) is a blood pressure-adjusted product of heart-ankle (ha) pulse wave velocity (PWV); the concept of CAVI is derived from the stiffness parameter β.
The β value for haPWV (haβ) is calculated using the following equation:1
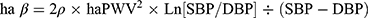
where ρ is blood density (fixed value of 1.05 in VS devices), Ln is natural logarithm, SBP is systolic blood pressure (SBP), and DBP is diastolic blood pressure (DBP).
CAVIvs is calculated using the following equation:1
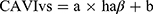
Regarding this equation, Takahashi et al disclosed that the coefficients “a” and “b” were changed by the haβ level (Table 1) to adjust haβ to Hasegawa-PWV (H-PWV). They explained the reason as follows:
Because haβ is based on PWV squared, whereas H-PWV is based solely on PWV, it is difficult to maintain a high correlation in a wide range of values with one approximate adjustment. For this reason, the portion that coincides with the correlation equation of haβ and H-PWV was defined as the middle range. For the upper and lower ranges that were outside the middle range, the coefficients were adjusted so that the difference between H-PWV and CAVI was small throughout the clinical range.1
 |
Table 1 The coefficients of a and b according to haβ and CAVIvs |
Here, a fundamental issue arises. Generally, the logic of the blood pressure (BP) independency of the stiffness parameter β is considered appropriate. However, originally, this hypothesis is to be applied on one arterial location. No logical explanation exists as to why this method is also perfectly valid in the evaluation of the long distant arteries with multiple segments. Nevertheless, we suppose that haβ is also BP independent. If we fix the coefficients of “a” and “b”, we can suppose that the characteristics of haβ is also reserved in all of the CAVIvs range. However, if coefficients “a” and “b” change according to the haβ value, the change in CAVIvs cannot properly reflect the original change in haβ when CAVIvs fluctuates across the points where the coefficients change (Figure 1). Therefore, the whole range of CAVIvs can never maintain the property of haβ nor stiffness parameter β. In fact, Lim et al demonstrated the difference between CAVIvs and the stiffness parameter β in a BP perturbation study.2 In this study, the change in CAVIvs correlated with that in BP, whereas the change in stiffness parameter β measured at the carotid segment did not. This indicates the BP dependency of CAVIvs and the difference between CAVIvs and “real” stiffness parameter β, although direct comparison was impossible due to different segments.
Regarding BP dependency of CAVI, Steppan et al demonstrated the BP dependency of CAVI in a rat model.3 Furthermore, Spronck et al and Segers elegantly proved the residual BP dependency of CAVI.4–6 Moreover, the author pointed out a fundamental discrepancy in BP measured using an oscillometric method from the internal arterial pressure measured with the catheter method.7
In addition, there will be also a fault in the equations introduced in the corresponding article.1 If we calculate haβ using typical haPWV value of 7 m/s (and SBP; 115 mmHg, DBP; 75 mmHg), the haβ is 1.10. The required haPWV to obtain the low cutoff haβ of 7.348 in several BP patterns is summarized in Table 2. The required haPWV values are considered too high for the middle-aged subjects with low cutoff haβ and CAVIvs because haPWV is inevitably much lower than baPWV due to the measurement process.8 Moreover, according to the study which adopted the same method using baPWV and central BP on the haβ equation,9 the central SBP was 115±1.0 mmHg (mean±standard error (SEM)), the central DBP was 75±1.0 mmHg (SEM), and the baPWV was 16±0.2 m/s (SEM). However, the “brachial-ankle β” was 5.6±0.1 (SEM), which is much lower than the low cutoff haβ of 7.348.
 |
Table 2 The haPWV to obtain haβ of 7.348 in various BP patterns |
In reality, the SI units should be used for the calculation, ρ should be 1500 kg/m3 (not 1.05 g/cm3 or 1.05 kg/L), and the unit of BP should be Pa (using the conversion value of 1 mmHg=133.32 kg/[m s2]).10 Table 3 shows the revision of Table 2 using SI units. The results are plausible for haPWV. Therefore, Takahashi et al should have clarified these points.1
 |
Table 3 The haPWV to obtain haβ of 7.348 in various BP patterns using SI units |
Tabara et al recently found the so-called regression-to-the-mean phenomenon after multivariate adjustment of the longitudinal change in CAVIvs (in about 5 years) in the general population.11 In this study, the most powerful independent determinant of the change in CAVIvs (⊿CAVIvs) was the baseline CAVIvs (standardized coefficient, −0.590; P<0.001). Moreover, ⊿CAVIvs was approximately −0.3 in the subjects with a baseline CAVIvs of ≥9.5, which indicated a decrease in CAVIvs in the multivariate adjusted model. The reason for these phenomena may be partly explained by the decrease in the coefficient “a” in the high range of haβ compared with that in the middle range of haβ.
Therefore, if we continue to use CAVIvs, we must be aware of the difference in CAVIvs from that of haβ when CAVIvs changes across the designated low and high points of CAVIvs (6.94 and 8.89, respectively). We must also recognize the substantial underestimation of the significance of high CAVIvs (>8.89) in regard to the original significance of the stiffness parameter β. Moreover, any fault in the corresponding article1 as pointed out above must be immediately amended.
Finally, if the original nature of stiffness β is to be properly adopted for haPWV in the VS device, the author suggests revalidation of the previous and upcoming data by fixing the coefficients or terminating the use of coefficients “a” and “b”. This will be the best way to use the concept of stiffness parameter β on PWV indices not only for ourselves but also for the researchers and the patients in the future. Grillo et al suggest that the calculation of β-stiffness index from PWV and BP-values is an interesting evolution that could overcome limitations and ambiguities derived from the BP dependency of the properties of the arterial wall, although the way of calculating this parameter is still debated.12 Combined use of the CAVI-0 method can be considered as well.4–7 Recently, Spronck et al presented an easy and useful method (using simple software, either Microsoft® Excel or PDF) to convert CAVIvs to CAVI0, which will greatly help in the simultaneous research on CAVIvs and CAVI0.13 The use of CAVIvs has spread widely. However, around 15 years have passed since it was produced, and it is used as a parameter only in VaSera. Conversely, adaptation of the stiffness β method on PWVs without using coefficients is the simplest method and will be available for the foreseeable future. In this situation, some difficulty is expected to emerge in the compatibility between CAVIvs and other PWV-derived stiffness β. As adequate data have been accumulated using VS, estimation of CAVI no longer has to rely on H-PWV data with deteriorating the nature of stiffness parameter β.
Acknowledgment
The author appreciates the researchers and participants of the preceding studies.
Disclosure
Dai Ato is a former employee of Fukuda Colin (formerly Omron Colin, Nippon Colin) Co., Ltd., a distributor of Vascular Profiler® (form PWV/ABI, BP-203RPE series). Dai Ato is an independent researcher and wrote this article as an academic activity based on the guaranteed right of freedom in academia for the Japanese (Article 23) and on the supreme law provided in Article 98 of the Constitution of Japan. Dai Ato reports no other conflicts of interest in this work.
References
1. Takahashi K, Yamamoto T, Tsuda S, et al. Coefficients in the CAVI equation and the comparison between CAVI with and without the coefficients using clinical data. J Atheroscler Thromb. 2019;26(5):465–475. doi:10.5551/jat.44834
2. Lim J, Pearman ME, Park W, Alkatan M, Machin DR, Tanaka H. Impact of blood pressure perturbations on arterial stiffness. Am J Physiol Regul Integr Comp Physiol. 2015;309(12):R1540–R1545. doi:10.1152/ajpregu.00368.2015
3. Steppan J, Sikka G, Hori D, et al. Seeking a blood pressure-independent measure of vascular properties. Hypertens Res. 2016;39(1):27–38. doi:10.1038/hr.2015.109
4. Spronck B, Avolio AP, Tan I, Butlin M, Reesink KD, Delhaas T. Arterial stiffness index beta and cardio-ankle vascular index inherently depend on blood pressure but can be readily corrected. J Hypertens. 2017;35(1):98–104. doi:10.1097/HJH.0000000000001132
5. Segers P. A lesson in vigilance: pressure dependency of a presumed pressure-independent index of arterial stiffness. J Hypertens. 2017;35(1):33–35. doi:10.1097/HJH.0000000000001139
6. Spronck B, Avolio AP, Tan I, Butlin M, Reesink KD, Delhaas T. Reply: physics cannot be disputed. J Hypertens. 2017;35(7):1523–1525. doi:10.1097/HJH.0000000000001350
7. Ato D. Brachial-ankle pulse wave velocity, cardio-ankle vascular index, and prognosis. Vasc Health Risk Manag. 2018;24(14):321–348. doi:10.2147/VHRM.S179366
8. Sugawara J, Hayashi K, Tanaka H. Arterial path length estimation on brachial-ankle pulse wave velocity: validity of height-based formulas. J Hypertens. 2014;32(4):881–889. doi:10.1097/HJH.0000000000000114
9. Kim T, Lee CS, Lee SD, et al. Impacts of comorbidities on the association between arterial stiffness and obstructive sleep apnea in the elderly. Respiration. 2015;89(4):304–311. doi:10.1159/000371768
10. Spronck B, Mestanik M, Tonhajzerova I, et al. Direct means of obtaining CAVI0-a corrected cardio-ankle vascular stiffness index (CAVI)-from conventional CAVI measurements or their underlying variables. Physiol Meas. 2017;38(10):N128–N137. doi:10.1088/1361-6579/aa8981
11. Tabara Y, Setoh K, Kawaguchi T, et al. Factors affecting longitudinal changes in cardio-ankle vascular index in a large general population: the Nagahama study. J Hypertens. 2018;36(5):1147–1153. doi:10.1097/HJH.0000000000001672
12. Grillo A, Salvi P. Cardio-ankle vascular index and carotid-femoral pulse wave velocity: limits and strengths. J Hypertens. 2018;36(4):759–764. doi:10.1097/HJH.0000000000001666
13. Spronck B, Mestanik M, Tonhajzerova I, et al. Easy conversion of cardio-ankle vascular index into CAVI0: influence of scale coefficients. J Hypertens. 2019;37(9):1913–1914. doi:10.1097/HJH.0000000000002166
 © 2019 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2019 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.

