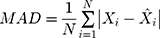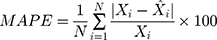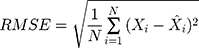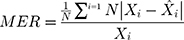Back to Journals » Infection and Drug Resistance » Volume 13
Estimating the Prevalence and Mortality of Coronavirus Disease 2019 (COVID-19) in the USA, the UK, Russia, and India
Authors Wang Y, Xu C, Yao S, Zhao Y, Li Y, Wang L, Zhao X
Received 30 May 2020
Accepted for publication 12 August 2020
Published 29 September 2020 Volume 2020:13 Pages 3335—3350
DOI https://doi.org/10.2147/IDR.S265292
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 4
Editor who approved publication: Professor Suresh Antony
Yongbin Wang,1,* Chunjie Xu,2,* Sanqiao Yao,1 Yingzheng Zhao,1 Yuchun Li,1 Lei Wang,3 Xiangmei Zhao1
1Department of Epidemiology and Health Statistics, School of Public Health, Xinxiang Medical University, Xinxiang, Henan Province, People’s Republic of China; 2Department of Occupational and Environmental Health, School of Public Health, Capital Medical University, Beijing, People’s Republic of China; 3Center for Musculoskeletal Surgery, Charité Universitätsmedizin Berlin, Corporate Member of Freie Universität Berlin, Humboldt-Universität Zu Berlin and Berlin Institute of Health, Berlin, Germany
*These authors contributed equally to this work
Correspondence: Yongbin Wang
Department of Epidemiology and Health Statistics, School of Public Health, Xinxiang Medical University, Xinxiang 453000, Henan Province, People’s Republic of China
Tel +86 373 383 1646
Email [email protected]
Objective: The aim of this study is to apply the advanced error-trend-seasonal (ETS) framework to forecast the prevalence and mortality series of COVID-19 in the USA, the UK, Russia, and India, and the predictive performance of the ETS framework was compared with the most frequently used autoregressive integrated moving average (ARIMA) model.
Materials and Methods: The prevalence and mortality data of COVID-19 in the USA, the UK, Russia, and India between 20 February 2020 and 15 May 2020 were extracted from the WHO website. Then, the data subsamples between 20 February 2020 and 3 May 2020 were treated as the training horizon, and the others were used as the testing horizon to construct the ARIMA models and the ETS models.
Results: Based on the model evaluation criteria, the ARIMA (0,2,1) and ETS (M,MD,N), sparse coefficient ARIMA (0,2,(1,6)) and ETS (A,AD,M), ARIMA (1,1,1) and ETS (A,MD,A), together with ARIMA (2,2,1) and ETS (A,M,A) specifications were identified as the preferred ARIMA and ETS models for the prevalence data in the USA, the UK, Russia, and India, respectively; the ARIMA (0,2,1) and ETS (M,A,M), ARIMA (0,2,1) and ETS (M,A,N), ARIMA (0,2,1) and ETS (A,A,N), coupled with ARIMA (0,2,2) and ETS (M,M,N) specifications were selected as the optimal ARIMA and ETS models for the mortality data in these four countries, respectively. Among these best-fitting models, the ETS models produced smaller forecasting error rates than the ARIMA models in all the datasets.
Conclusion: The ETS framework can be used to nowcast and forecast the long-term temporal trends of the COVID-19 prevalence and mortality in the USA, the UK, Russia, and India, and which provides a notable performance improvement over the most frequently used ARIMA model. Our findings can aid governments as a reference to prepare for and respond to the COVID-19 pandemic both in restricting the transmission of the disease and in lowering the disease-related deaths in the upcoming days.
Keywords: coronavirus disease 2019, outbreak, ARIMA model, ETS model, epidemiological indicators, nowcasting
Introduction
Coronavirus disease 2019 (COVID-19) is an acute respiratory contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2).1,2 This disease was considered to be first detected in the city of Wuhan, China, in December 2019. Since then, COVID-19 has spread rapidly from almost every corner of the world, and, currently, has been presenting a global pandemic that leads to a great tragedy.3 As of May 15, 2020, the number of confirmed COVID-19 cases has totaled 4,338,658 notifications and has caused 297,119 deaths in 213 countries, areas or territories worldwide.4 Furthermore, it is likely that numerous infected individuals failed to be found because of the limited epidemiological surveillance and detection capabilities on the global scale.3 Unfortunately, there is a present scarcity of the determined clinical treatment for this disease. In this case, accurate forecasting for the upcoming daily prevalence and mortality cases can contribute to plan the health infrastructure and services under dynamic demand and to guide emergency preparedness effectively in responding to the disease outbreak.
Time series analysis based on mathematical models is of great value in constructing hypotheses to show inherent patterns and underlying structures based on the prevalence and mortality data, and to predict the epidemics of diseases.3,5–7 Also, stakeholders can apply the time series from the past and present outbreaks to forecast prevalence rates and then identifying how to limit the spread of the virus, and ultimately introducing the most effective vaccination policies.5 Numerous modeling techniques (such as machine learning method,8 general linear model,9 spatiotemporal approach,5 artificial neural networks (ANNs),10 grey GM (1,1) model,11 autoregressive integrated moving average (ARIMA),12 support vector machine (SVM) regression model,13 multivariate time series analysis,14 and susceptible-exposed-infectious-recovered (SEIR) model)15 that serve as helpful policy-supportive tools have been utilized to model and estimate the epidemic patterns and even the outbreak of infectious diseases. Among which, the most commonly adopted methods for various predictive objectives are either the linear models (such as general linear model, GM (1,1), and ARIMA) or the nonlinear models (such as SVM and ANNs).12,16 Epidemics of infectious diseases are often affected and restricted by varying influencing factors (such as meteorological factors, variations in pathogens, or policy interventions),17–20 which means that the epidemic patterns contain both linear and nonlinear components (that is, including both tendencies and randomness).3,19 Under this condition, the basic linear or nonlinear approaches are only sufficient to uncover the epidemic tendencies or randomness, which limits the generalization ability of these basic models.
Over the last decades, though the popular exponential smoothing (ES) approaches under a linear assumption have extensively been adopted for different predictive purposes,21 paralleling the methodological developments, researchers have relaxed the linear assumption of the ES approaches by embedding them in a modern nonlinear model framework, called Error-Trend-Seasonal (ETS) framework (which signifies the three traits including error, trend, and seasonality of a time series).22–26 Such a framework may be more suitable for handling such data with different traits because they take into consideration the possible additive or multiplicative combinations of the secular trend, seasonal pattern, and random disturbances of the data with 30 candidate models.19,22,26,27 Recently, researchers have shown an increased interest in the domain of forecasting (such as the forecast for the electricity consumption,28 electricity generation,29 bond yields,29 the number of tourists,29 acute hemorrhagic conjunctivitis incidence,25 and tuberculosis incidence)22 with the ETS framework due to its so many advantages. The ETS models are greatly helpful in capturing the dynamic dependence structure of a target series, considering the rapid fluctuation, changing trends, cyclic variation, and random fluctuation in the given series.
Most recently, a large number of models have been used to nowcast and forecast the epidemic patterns of COVID-19 pandemic around the world, such as ARIMA model,3,30–32 machine-learning model,8 spatiotemporal approach,5 Bats-Hosts-Reservoir-People transmission network model,33 data mining approach based on a 3rd degree polynomial curve,7 SEIR or SIR model,18,34 internet search-interest based model,9 ad hoc,35 fixed-effects linear model,36 adaptive neuro-fuzzy inference system (ANFIS) model,37 etc. However, most of these models are focused on a short-term estimation for the COVID-19 incidence, mortality, or prevalence, and they can only unearth the linear or nonlinear components in a given series. There is a need to construct a statistical model that can consider both linear and nonlinear components in a target time series simultaneously to assess the epidemic situations and trends of COVID-19. So far, there are no studies that use the ETS framework to estimate the COVID-19 prevalence and mortality. Therefore, in view of the advantages of the ETS framework and the current epidemic status of COVID-19 with the rapidly increased cases per day in the USA, the UK, Russia, and India,4 the aim of this work is to use the ETS framework to analyze the epidemic situation of COVID-19 and to nowcast and forecast the temporal trends of COVID-19 prevalence and mortality in the USA, the UK, Russia, and India. Also, we compared the predictive performance of the ETS framework with the most used ARIMA model in the field of time series prediction. The results will provide a scientific basis for defining strategic choices both in limiting the transmission of COVID-19 and in lowering the disease-related incidence and mortality.
Materials and Methods
Data Collection
The number of clinically diagnosed or laboratory-confirmed COVID-19 cases and deaths by countries, territories or areas must be reported to the WHO per day, so we extracted the key epidemiological indicators of COVID-19 (such as prevalence, mortality, incidence, and fatality cases) in the USA, the UK, Russia, and India between 20 February 2020 and 15 May 2020 from the WHO website (https://www.who.int/emergencies/diseases/en/). As shown in Figure 1, during the study period, the number of confirmed COVID-19 cases totaled 1,361,522 notifications with a daily average of 15,832 cases in the USA, 233,155 notifications with a daily average of 2712 cases in the UK, 262,843 notifications with a daily average of 3056 cases in Russia, and 81,970 notifications with a daily average of 954 cases in India. The number of deaths owing to COVID-19 totaled 83,543 notifications with a daily average of 972 cases in the USA, 33,614 notifications with a daily average of 391 cases in the UK, 2418 notifications with a daily average of 29 cases in Russia, and 2649 notifications with a daily average of 31 cases in India.
Ethics Statement
The study protocol was approved by the research institutional review board of the Xinxiang Medical University (No: XYLL-2019072), and it is exempt from the institutional review board assessment since all data are publicly available. Besides, this research meets all the guidelines in the Declaration of Helsinki.
ARIMA Model
The ARIMA model, also known as the Box–Jenkins model, has been identified as being the most common forecasting tool as it has the advantages of simple structure, predictive stability, and ability to well explain the given series.3,38 The traditional ARIMA model can be listed using the standard notation of ARIMA (p, d, q), where p denotes the order of autoregressive parameters, d denotes the degree of differencing, and q denotes the order of moving average parameters.12 In application, the ARIMA model was often constructed following four key steps (Figure S1): First, checking the stationary of the target series. We determined the stationary of the target series by a visual inspection of the sequence plot and the Augmented Dickey–Fuller (ADF) test, if the series exhibits a clear upward or downward trend and the ADF statistic indicates a p-value greater than 0.05, meaning that the series is non-stationary.16,30 In this scenario, the series should be square root- or log-transformed, and/or be differenced in order to suit the requirement of stationary for the ARIMA-developing model.22 Second, estimating the model fit. The possible p and q values were identified roughly by plotting the autocorrelation function (ACF) and partial ACF (PACF) graphs on the basis of the stationary series.30 As such, some candidate models were chosen. Of them, the one that has the largest values of R-square (R2) and stationary R2, as well as the lowest normalized Bayesian information criterion (NBIC) value was deemed as the best-fitting model.39 Third, checking the goodness of fit measures for the optimal model. The determined key parameters of the best-mimicking ARIMA model indicated a significantly statistical difference and the produced error series displayed a white noise under the Ljung–Box Q test, intimating that the selected model is adequate for modeling the temporal dependence structure of the prediction object.40 Otherwise, the above steps should be repeated until a suitable model was detected. Finally, the best-conducting ARIMA model created can be applied to produce forecasting into the future.41
ETS Model
Typically, a time series is composed of three components, including the secular trend (T), seasonality (S), and error (E).3,23 Among them, the trend component reflects the secular movement of the given series, the seasonal component characterizes a pattern with known cyclicity, and the random disturbances represent the irregular and unpredictable traits of the series.28 Moreover, these three components may be combined in different additive or multiplicative combinations to generate the original series Y, which may only have an additive model like Y=T+S+E or Y=S+E, a pure multiplicative model, say Y=T·S·E or Y=S·E, or models that are comprised of the above mixture, as in Y= (T·S)+E or Y= (T+S)(1+E).24,29,42,43 Under these scenarios, the other frequently used models may be incapable of capturing the potential relationships in the time series owing to their linear or nonlinear assumptions.22 In contrast to the basic linear or nonlinear models, the ETS framework provides an expansion for the basic ES approaches and a theoretical foundation for the estimate of the basic ES approaches with state-space based likelihood calculations,22,26 and moreover, this framework supports model choice and estimation of predictive standard errors. By doing so, not only will the ETS models be able to reflect the internal rules of the target series but they are also able to explore the dynamic association between the internal rules and the external outputs, and can to describe the internal rules of the target series with the present and past minimum information.21,24 These enable the ETS models to have the ability to model any given series even with both heterogeneity and non-linearity and to perform a long-run forecast for the given series. The individual components of an ETS specification are summarized in Table 1. For any ETS models, their parameters and values for the initial states can be expressed as being of the form: 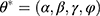 and
and 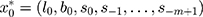 , respectively, where
, respectively, where 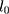 is the level term of the trend which is invariably present,
is the level term of the trend which is invariably present, 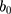 is the growth term of the trend which may be present depending on the trend specification, s denotes the seasonal term of the target series, and m represents the periodic length of the target series. Often, for a classical curve of an epidemiological outbreak of infectious diseases (spark-growth-peak-decrease), its growth rate at the end of the past series is unlikely to continue more than a short time into the future. At this time, the ETS model with a damped trend term is greatly suitable when the long-term trend is included in the target time series because it can dampen the trend with the length of the forecast horizon increases, which can frequently favor the improvement of the predictive ability of the ETS models.24 Of the above 30 possible methods, we determined which one more closely simulates the target series by comparing the goodness of fit measures across models, including the Akaike Information Criterion (AIC), the Schwarz Information Criterion (BIC), the Hannan–Quinn Criterion (HQ), the average mean square error (AMSE), and the Log-likelihood (LL).22,25 The specification with lower values of the AIC, BIC, HQ, and AMSE, as well as a higher LL value, was recommended as the preferred.
is the growth term of the trend which may be present depending on the trend specification, s denotes the seasonal term of the target series, and m represents the periodic length of the target series. Often, for a classical curve of an epidemiological outbreak of infectious diseases (spark-growth-peak-decrease), its growth rate at the end of the past series is unlikely to continue more than a short time into the future. At this time, the ETS model with a damped trend term is greatly suitable when the long-term trend is included in the target time series because it can dampen the trend with the length of the forecast horizon increases, which can frequently favor the improvement of the predictive ability of the ETS models.24 Of the above 30 possible methods, we determined which one more closely simulates the target series by comparing the goodness of fit measures across models, including the Akaike Information Criterion (AIC), the Schwarz Information Criterion (BIC), the Hannan–Quinn Criterion (HQ), the average mean square error (AMSE), and the Log-likelihood (LL).22,25 The specification with lower values of the AIC, BIC, HQ, and AMSE, as well as a higher LL value, was recommended as the preferred.
 |
Table 1 The 30 Possible ETS Models in Relation to Different Combinations of Trend, Seasonality and Residual |
Assessing Model Performance
We evaluated the accuracy of forecasts between the ARIMA model and the ETS model by comparing four statistical measures of error, namely the mean absolute deviation (MAD), the mean absolute percentage error (MAPE), the root-mean-squared error (RMSE), and the mean error rate (MER). The model with the lowest values across these four measures can more closely fit the target series.
where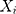 signifies the observed values,
signifies the observed values,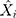 denotes the fitted and predicted results,
denotes the fitted and predicted results,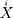 signifies the mean values of the target series, and
signifies the mean values of the target series, and 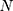 denotes the number of data points. To develop an ARIMA model with high accuracy and strong robustness, at least 50 data points are required.44 Thus, in this time series analysis, the data subsamples (74 observations) between 20 February 2020 and 3 May 2020 were treated as the training horizon, and the others (12 observations) were used as the testing horizon to compare the predictive performance between the ARIMA model and the ETS model. Subsequently, we re-created the ETS models based on the whole prevalence and mortality data to undertake forecasting for the upcoming future. Data analyses were performed using SPSS software (version 17.0, IBM Corp, Armonk, NY), R software (version 3.4.3, R Development Core Team, Vienna, Austria), and Eviews10.0 software (IHS, Inc. USA). A p-value of less than 0.05 indicates a statistical difference.
denotes the number of data points. To develop an ARIMA model with high accuracy and strong robustness, at least 50 data points are required.44 Thus, in this time series analysis, the data subsamples (74 observations) between 20 February 2020 and 3 May 2020 were treated as the training horizon, and the others (12 observations) were used as the testing horizon to compare the predictive performance between the ARIMA model and the ETS model. Subsequently, we re-created the ETS models based on the whole prevalence and mortality data to undertake forecasting for the upcoming future. Data analyses were performed using SPSS software (version 17.0, IBM Corp, Armonk, NY), R software (version 3.4.3, R Development Core Team, Vienna, Austria), and Eviews10.0 software (IHS, Inc. USA). A p-value of less than 0.05 indicates a statistical difference.
Results
Developing the ARIMA Models
Applying the ADF test to the prevalence and mortality time series of COVID-19 in the USA, the UK, Russia, and India suggesting a unit root present in these series, and given the prevalence and mortality time series plots showing a rising trend (Figure 1), these meant that the variance of the object series varied over time and they were non-stationary. So we performed the log-transformation or square root-transformation and differences for all the series, and the resulting results are presented in Table S1, indicating that the target series became stationary (p<0.05) after taking either the first- or second-order difference. Next, we determined the possible parameters of ARIMA models by comparing the ACF and PACF plots based on these stationary series (Figures S2 and S3), all the candidate ARIMA models created for the prevalence and mortality time series of COVID-19 are listed in Table S2. Of these models, the best-fitting models for the different target series were further detected according to the goodness of fit tests and the residual ACF and PACF plots (Table 2, Figures 2 and 3), the results suggested that the ARIMA (0,2,1), sparse coefficient ARIMA (0,2,(1,6)), ARIMA (1,1,1), and ARIMA (2,2,1) specifications were identified as being the preferred models for the prevalence data in the USA, the UK, Russia, and India, respectively, and the ARIMA (0,2,1), ARIMA (0,2,1), ARIMA (0,2,1), and ARIMA (0,2,2) specifications were selected as the optimal models for the mortality data in these four countries, respectively, in that the above models had larger R2 and stationary R2 values, along with a smaller NBIC value, and all the residual series displayed a white noise owing to the p-values greater than 0.05 under the Ljung–Box Q tests in addition to the residuals for the prevalence data in Russia, where the Ljung–Box Q test showed a p-value less than 0.05 among all the possible ARIMA models. Moreover, among the optimal ARIMA models for the prevalence and mortality data in these four countries, the determined parameters indicated a statistical significance. All the above-mentioned intimated that the chosen ARIMA methods are adequate for modeling the temporal dependence structures of the COVID-19 prevalence and mortality data in the USA, the UK, Russia, and India. Therefore, these preferred models determined can be utilized to analyze and estimate the epidemics in the upcoming days.
 |
Table 2 Estimated Parameters of the Best-Fitting ARIMA Methods and Their Goodness of Fit Test Results for the Prevalence and Mortality of COVID-19 in These Four Countries |
Developing the ETS Models
After applying the ETS models to the prevalence and mortality data of COVID-19, we determined the preferred ETS specifications for the target series by comparing different statistical indices, and the estimated parameters and their goodness of fit test results are given in Tables S3-S11. Among all the possible models, the ETS (M,MD,N), ETS (A,AD,M), ETS (A,MD,A), and ETS (A,M,A) specifications were considered as the optimal models for the prevalence data, and the ETS (M,A,M), ETS (M,A,N), ETS (A,A,N), and ETS (M,M,N) specifications were recommended as the preferred models for the mortality data in the USA, the UK, Russia, and India, respectively, as these chosen models gave lower values of the AIC, BIC, HQ, and AMSE, together with greater values of the LL and compact LL (Table 3). These best-fitting ETS specifications can then be employed to conduct forecasting for the prevalence and mortality data in the USA, the UK, Russia, and India in the near future.
 |
Table 3 Estimated Parameters of the Best-Fitting ETS Methods and Their Goodness of Fit Test Results for the Prevalence and Mortality of COVID-19 in These Four Countries |
Assessing the Predictive Ability Between Models
Table 4 provides the summary statistics for the forecasting ability between the best-fitting ARIMA models and the best-fitting ETS models, it can be seen from the data in this table that the ETS models reported the errors significantly lower than the ARIMA models for the prevalence and mortality testing data in the USA, the UK, Russia, and India, which showed that the ETS models are well suitable for tracking the dynamic dependence structure of the prevalence and mortality data of COVID-19. As such, we re-modeled the ETS models based on the entire data from 20 February 2020 to 15 May 2020 to nowcast and forecast the prevalence and mortality of COVID-19 between 16 May 2020 and 31 May 2020 (future 16 days) (the estimated parameters are presented in Table S12). As illustrated in Tables 5 and 6, Figure 4, the next 16-day forecasts of the prevalence and mortality cases may be 1,640,383 (95% uncertainty interval [UI] 1,454,307 to 1,826,458) and 102,785 (95% UI 84,903 to 120,666) in the USA, respectively, 278,912 (95% UI 245,286 to 312,539) and 39,696 (95% UI 30,948 to 48,444) in the UK, respectively, 425,838 (95% UI 54,126 to 2,693,247) and 3785 (95% UI 3227 to 4343) in Russia, respectively, and 133,806 (95% UI 120,383 to 147,229) and 4127 (95% UI 3527 to 4728) in India, respectively.
 |
Table 4 Comparisons of Predictive Performances for the Prevalence and Mortality of COVID-19 Between the Best-Fitting ETS and ARIMA Models in These Four Countries |
 |
Table 5 Projection of the COVID-19 Prevalence into the Next 16 Days Using the ETS Models Based on the Entire Data |
 |
Table 6 Projection of the COVID-19 Mortality Cases into the Next 16 Days Using the ETS Models Based on the Entire Data |
Discussion
Early nowcasting for the epidemic patterns of the COVID-19 key epidemiological indicators (eg, prevalence, mortality, incidence, and fatality cases) is essential to define strategic preparedness and response plan (eg, implementation of the adequate health interventions, rational allocation of the limited health resources, regulation of the production activities, etc.) both in restricting the transmission of the disease and in lowering the disease-related deaths.3,5,6,18,35,45 Therefore, it is imperative to develop adequate warning models that can aid governments in acting as a reference to prepare for and respond to this crisis consistent with the strategic preparedness and response plan. In this work, we described the current epidemics of the COVID-19 in the USA, the UK, Russia, and India, and nowcasted the extent and duration of the prevalence and mortality time series using the advanced ETS models, and the predictive ability of the ETS models for various datasets was compared with the ARIMA model that was recommended as being the most commonly used time series forecasting tool.46 Our results indicated that the ETS models can better track the dynamic dependence structures of various datasets in the forecasting aspect than that in the ARIMA models. Furthermore, the ETS models provided a highly accurate estimation as the predictive performance provided MAPE values of less than 10% in the different testing data.47 Thus, the ETS framework can be recommended as a flexible and instrumental tool to nowcast and forecast the prevalence and mortality trends of COVID-19.
The ETS models can also play a pivotal role in estimating the effects of current and future prevention and control measures taken for the COVID-19 pandemic (eg, lockdown, an optimization of the present tools, an introduction of the available vaccine, increasing intensive care unit availability, an increase in the number of mobile cabin hospitals, and/or other intervention strategies).1,7,20,48,49 If our ETS models eventually gave an overestimation for the epidemiological trends of the prevalence and mortality of the COVID-19 pandemic, meaning that the current countermeasures play a role; otherwise, additional prevention and control measures are required to prepare for and response to the COVID-19 outbreak. To our best knowledge, this is the only study to perform the prevalence and mortality time series forecasting of the COVID-19 pandemic using the advanced ETS models in the USA, the UK, Russia, and India, and our findings from different prevalence and mortality datasets confirmed the flexibility and usefulness of the ETS models in forecasting the outbreak of COVID-19. Besides, recent studies have demonstrated that some hybrid models can also provide a close approximation to the temporal patterns of the COVID-19 outbreak.50,51 For example, Singh et al proposed a new hybrid model by combining wavelet decomposition and ARIMA model to make forecasting for the total death cases of COVID-19 in Italy, Spain, France, the UK, and the USA.51 Chakraborty et al developed a novel hybrid ARIMA-wavelet-based forecasting (WBF) model to make real-time forecasts and risk assessment for the morbidity cases of COVID-19 in India, Canada, France, South Korea, and the UK.50 Therefore, future work is supposed to compare the reliability level in forecasting the epidemiological indicators of the COVID-19 outbreak between the ETS model and the mentioned hybrid techniques. Also, it should be noted that there may be underfitting or overfitting in the process of establishing the ETS framework, which may affect the predictive performance of the ETS model.22 In this study, to prevent the ETS model from underfitting or overfitting, we determined the preferred ETS framework based on multiple goodness of fit measures such as AIC, BIC, HQ, AMSE, and LL, and if these measures displayed the same values between the training horizon and the testing horizon simultaneously, and then this ETS model could be recommended as the optimal specification.
Currently, great concerns are that the health system capacity in the countries of the COVID-19 outbreak can effectively meet the need of the infected persons who are hospitalized or require intensive care and whether there are a sufficient number of doctors and nurses, as well as personal protective gear. Particularly in the USA, the total confirmed cases and deaths showed a rapid rise since 18 March 2020, and the current epidemic trends still remain relatively high levels in the morbidity and mortality of COVID-19. Unfortunately, according to the projections into the next 16 days (Figure 4A), it appeared that the daily confirmed cases and deaths may continue to increase with a daily average of 17,429 and 1203 cases, respectively, and the estimated total prevalence and mortality cases may reach 1,640,383 (95% UI 1,454,307 to 1,826,458) and 102,785 (95% UI 84,903 to 120,666), respectively (Tables 5 and 6). Therefore, it is essential to continuously implement strict prevention and control strategies in the USA. Meanwhile, Russia, the second-worst-hit country with a total of 262,843 confirmed cases and 2418 deaths around the world, is still experiencing a remarkable rise in the incidence and mortality of COVID-19. Regrettably, similar to the USA, the estimated confirmed cases and deaths may continue to increase with a daily average of 10,188 and 86 cases, respectively (Figure 4C), and the aggregated confirmed cases and deaths may be 425,838 (95% UI 54,126 to 2,693,247) and 3785 (95% UI 3227 to 4343), respectively, in the next 16 days (Tables 5 and 6). Likewise, India is also witnessing a rapid increase in the reported cases and deaths of COVID-19 (Figure 4D), the estimated confirmed cases and deaths may continue to increase with a daily average of 3240 and 93 cases, respectively, and the accumulative reported cases and deaths may reach 133,806 (95% UI 120,383 to 147,229) and 4127 (95% UI 3527 to 4728), respectively, in the next 16 days (Tables 5 and 6). Contrast to the continued increase in the numbers of reported confirmed cases and deaths of COVID-19 in the USA, Russia, and India, it seems that the daily new notified cases and deaths have reached the plateau in the UK as the total number of estimated reported cases and deaths owing to COVID-19 may be 278,912 (95% UI 245,286 to 312,539) and 39,696 (95% UI 30,948 to 48,444), respectively, with a daily average of 2859 notified cases and 381 deaths in the next 16 days (Tables 5 and 6, Figure 4B), which was well below the daily average numbers of new cases (4690) and deaths (699) due to COVID-19 between 1 April 2020 and 15 May 2020. Overall, strict prevention and control strategies should be conducted in the USA, the UK, Russia, and India to control the COVID-19 outbreak, although a downward trend was seen in the UK in the next 16-day forecasts. If the COVID-19 pandemic failed to be controlled, then these countries will encounter a severe shortage of hospitals, which will make the upcoming situation of COVID-19 pandemic even worse, and thus may lead to an unprecedented disaster.
There are several limitations to this study. First, accurate statistics on the key epidemiological indicators of COVID-19 (such as prevalence, mortality, incidence, and fatality cases) are crucial for the ETS model development, whereas the limited epidemiological surveillance and detection capabilities may cause underestimations for the mentioned epidemiological indicators in the study regions. Second, whether the ETS framework can provide an accurate forecast for the prevalence and mortality time series of COVID-19 in other countries, areas or territories, it is required to perform further validation. Lastly, the forecasting accuracy level of the ETS framework may be deteriorated as the increase in the predicted length of time, and thus the prevalence and morbidity samples are expected to be updated in real-time.
Conclusions
Accurate forecasting for the prevalence and mortality trends of COVID-19 can contribute to plan the health infrastructure and services under dynamic demand and to guide emergency preparedness effectively in responding to this disease outbreak. In this work, the ETS framework can be used to nowcast and forecast the long-term temporal trends of the COVID-19 prevalence and mortality in the USA, the UK, Russia, and India, and which provides a notable performance improvement over the most frequently used ARIMA model. Our findings can aid governments as a reference to prepare for and respond to the COVID-19 pandemic consistent with the strategic preparedness and response plan (eg, implementation of the adequate health interventions, rational allocation of the limited health resources, regulation of the production activities, etc.) both in restricting the transmission of the disease and in lowering the disease-related deaths in the upcoming days. However, for more accurate estimates and future perspectives, the prevalence and mortality series should be updated in time.
Data Sharing Statement
All data can be extracted from the WHO website.
Acknowledgments
We appreciated the WHO for providing these data. This project was supported by the Innovation Project for College Students of Xinxiang Medical University (code: XYXSKYZ201932) and the Key Scientific Research Project of Universities in Henan (code: 21A330004).
Author Contributions
All authors contributed to data analysis, drafting or revising the article, gave final approval of the version to be published, and agree to be accountable for all aspects of the work.
Disclosure
The authors report no conflicts of interest for this work.
References
1. Pan A, Liu L, Wang C, et al. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA. 2020;323(19):1915. doi:10.1001/jama.2020.6130
2. Zhou P, Yang XL, Wang XG, et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579(7798):270–273. doi:10.1038/s41586-020-2012-7
3. Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci Total Environ. 2020;729:138817. doi:10.1016/j.scitotenv.2020.138817
4. World Health Organization. Coronavirus disease (COVID-2019) situation reports. Available from: https://www.who.int/emergencies/diseases/novel-coronavirus −2019/situation-reports/2020.
5. Bekiros S, Kouloumpou D. SBDiEM: A new mathematical model of infectious disease dynamics. Chaos Soliton Fract. 2020;136:109828. doi:10.1016/j.chaos.2020.109828
6. Li J, Wang Y, Gilmour S, Wang M, Hao Y. Estimation of the epidemic properties of the 2019 Novel Coronavirus: a mathematical modeling study. SSRN Electronic J. 2020.
7. Sotgiu G, Gerli AG, Centanni S, et al. Advanced forecasting of SARS-CoV-2-related deaths in Italy, Germany, Spain, and New York State. Allergy. 2020;75(7):1813–1815. doi:10.1111/all.14327
8. Vaid S, Cakan C, Bhandari M. Using machine learning to estimate unobserved COVID-19 Infections in North America. J Bone Joint Surg Am. 2020;102(13):e70. doi:10.2106/JBJS.20.00715
9. Yuan X, Xu J, Hussain S, Wang H, Gao N, Zhang L. Trends and prediction in daily new cases and deaths of COVID-19 in the united states: an internet search-interest based model. Explor Res Hypothesis Med. 2020;5(2):1–6. doi:10.14218/erhm.2020.00023
10. Shafaei M, Adamowski J, Fakherifard A, Dinpashoh Y, Adamowski K. A wavelet-SARIMA-ANN hybrid model for precipitation forecasting. J Water Land Development. 2016;28(1):27–36. doi:10.1515/jwld-2016-0003
11. Wang YW, Shen ZZ, Jiang Y. Comparison of ARIMA and GM(1,1) models for prediction of hepatitis B in China. PLoS One. 2018;13(9):e0201987. doi:10.1371/journal.pone.0201987
12. Li Z, Wang Z, Song H, et al. Application of a hybrid model in predicting the incidence of tuberculosis in a Chinese population. Infect Drug Resist. 2019;12:1011–1020. doi:10.2147/idr.s190418
13. Liang F, Guan P, Wu W, Huang D. Forecasting influenza epidemics by integrating internet search queries and traditional surveillance data with the support vector machine regression model in Liaoning, from 2011 to 2015. Peer J. 2018;6:e5134. doi:10.7717/peerj.5134
14. Zhang T, Yin F, Zhou T, Zhang XY, Li XS. Multivariate time series analysis on the dynamic relationship between Class B notifiable diseases and gross domestic product (GDP) in China. Sci Rep. 2016;6(1):29. doi:10.1038/s41598-016-0020-5
15. Borracci RA, Giglio ND. Forecasting the effect of social distancing on COVID-19 autumn-winter outbreak in the metropolitan area of Buenos Aires. Medicina. 2020;80(Suppl 3):7–15.
16. Liu Q, Li Z, Ji Y, et al. Forecasting the seasonality and trend of pulmonary tuberculosis in Jiangsu Province of China using advanced statistical time-series analyses. Infect Drug Resist. 2019;12:2311–2322. doi:10.2147/idr.s207809
17. Juni P, Rothenbuhler M, Bobos P, et al. Impact of climate and public health interventions on the COVID-19 pandemic: a prospective cohort study. CMAJ. 2020;192(21):E566E573. doi:10.1503/cmaj.200920
18. JT W, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi:10.1016/s0140-6736(20)30260-9
19. Wang Y, Xu C, Zhang S, Wang Z, Zhu Y, Yuan J. Temporal trends analysis of human brucellosis incidence in mainland China from 2004 to 2018. Sci Rep. 2018;8(1):15901. doi:10.1038/s41598-018-33165-9
20. Wu Y, Jing W, Liu J, et al. Effects of temperature and humidity on the daily new cases and new deaths of COVID-19 in 166 countries. Sci Total Environ. 2020;729:139051. doi:10.1016/j.scitotenv.2020.139051
21. Chatfield C, Koehler AB, Ord JK, Snyder RD, New A. Look at Models For Exponential Smoothing. J R Stat Soc. 2001;50(2):147–159. doi:10.1111/1467-9884.00267
22. Wang Y, Xu C, Ren J, et al. Secular seasonality and trend forecasting of tuberculosis incidence rate in china using the advanced error-trend-seasonal framework. Infect Drug Resist. 2020;13:733–747. doi:10.2147/IDR.S238225
23. Ke G, Hu Y, Huang X, et al. Epidemiological analysis of hemorrhagic fever with renal syndrome in China with the seasonal-trend decomposition method and the exponential smoothing model. Sci Rep. 2016;6:39350. doi:10.1038/srep39350
24. Hyndman RJ, Koehler AB, Keith OJ, Snyder RD. Forecasting with Exponential Smoothing the State Space Approach. berlin: springerverlag; 2008.
25. Liu H, Li C, Shao Y, et al. Forecast of the trend in incidence of acute hemorrhagic conjunctivitis in China from 2011-2019 using the Seasonal Autoregressive Integrated Moving Average (SARIMA) and Exponential Smoothing (ETS) models. J Infect Public Health. 2020;13(2):287–294. doi:10.1016/j.jiph.2019.12.008
26. Ord JK, Koehler AB, Snyder RD. Estimation and prediction for a class of dynamic nonlinear statistical models. J Am Stat Assoc. 1997;92(440):1621–1629. doi:10.1080/01621459.1997.10473684
27. Hyndman RJ, Koehler AB, Snyder RD, Grose S. A state space framework for automatic forecasting using exponential smoothing methods. Int J Forecasting. 2000;18(3):439–454. doi:10.1016/S0169-2070(01)00110-8
28. Deb M, Chakrabarty TK. A wavelet based hybrid SARIMA-ETS model to forecast electricity consumption. EJASA. 2017;10(2):408–430.
29. Hyndman RJ, Khandakar Y. Automatic time series forecasting: the forecast package for R. J Stat Softw. 2008;27(3):1–22. doi:10.18637/jss.v027.i03
30. Benvenuto D, Giovanetti M, Vassallo L, Angeletti S, Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief. 2020;29:105340. doi:10.1016/j.dib.2020.105340
31. Moftakhar L, Seif M. The exponentially increasing rate of patients infected with COVID-19 in Iran. Arch Iran Med. 2020;23(4):235–238. doi:10.34172/aim.2020.03
32. Ahmar AS, Del Val EB. SutteARIMA: short-term forecasting method, a case: COVID-19 and stock market in Spain. Sci Total Environ. 2020;729:138883. doi:10.1016/j.scitotenv.2020.138883
33. Chen TM, Rui J, Wang QP, Zhao ZY, Cui JA, Yin L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect Dis Poverty. 2020;9(1):24. doi:10.1186/s40249-020-00640-3
34. Wan K, Chen J, Lu C, Dong L, Wu Z, Zhang L. When will the battle against novel coronavirus end in Wuhan: A SEIR modeling analysis. J Glob Health. 2020;10(1):011002. doi:10.7189/jogh.10.011002
35. Tang Y, Wang S. Mathematic modeling of COVID-19 in the United States. Emerging Microbes Infections. 2020;9(1):827–829. doi:10.1080/22221751.2020.1760146
36. Sarkodie SA, Owusu PA. Investigating the cases of novel coronavirus disease (COVID-19) in China using dynamic statistical techniques. Heliyon. 2020;6(4):e03747. doi:10.1016/j.heliyon.2020.e03747
37. Al-Qaness MAA, Ewees AA, Fan H. Optimization method for forecasting confirmed cases of COVID-19 in China. J Clin Med. 2020;9(3):674. doi:10.3390/jcm9030674
38. Zheng A, Fang Q, Zhu Y, Jiang C, Jin F, Wang X. An application of ARIMA model for predicting total health expenditure in China from 1978-2022. J Glob Health. 2020;10(1):010803. doi:10.7189/jogh.10.010803
39. Cao LT, Liu HH, Li J, Yin XD, Duan Y, Wang J. Relationship of meteorological factors and human brucellosis in Hebei province, China. Sci Total Environ. 2020;703:135491. doi:10.1016/j.scitotenv.2019.135491
40. Wang Y, Xu C, Wang Z, Yuan J. Seasonality and trend prediction of scarlet fever incidence in mainland China from 2004 to 2018 using a hybrid SARIMA-NARX model. Peer J. 2019;7:e6165. doi:10.7717/peerj.6165
41. Zheng Y, Zhang L, Wang L, Rifhat R. Statistical methods for predicting tuberculosis incidence based on data from Guangxi, China. BMC Infect Dis. 2020;20(1):300. doi:10.1186/s12879-020-05033-3
42. EViews Help: user’s Guide. Available from: http://www.eviews.com/help/helpintro. html#page/content/preface.html.
43. Taylor JW. Exponential smoothing with a damped multiplicative trend. Int J Forecasting. 2003;19(4):715–725. doi:10.1016/S0169-2070(03)00003-7
44. Bartholomew D, Box GEP, Jenkins GM. Time Series Analysis: Forecasting and Control.
45. Li Q, Feng W, Quan YH. Trend and forecasting of the COVID-19 outbreak in China. J Infect. 2020;80(4):469–496. doi:10.1016/j.jinf.2020.02.014
46. He F, Hu ZJ, Zhang WC, Cai L, Cai GX, Aoyagi K. Construction and evaluation of two computational models for predicting the incidence of influenza in Nagasaki Prefecture, Japan. Sci Rep. 2017;7(1):7192. doi:10.1038/s41598-017-07475-3
47. HT P. Forecasting energy consumption in Taiwan using hybrid nonlinear models. Energy. 2009;34(10):1438–1446. doi:10.1016/j.energy.2009.04.026
48. Gupta S, Raghuwanshi GS, Chanda A. Effect of weather on COVID-19 spread in the US: A prediction model for India in 2020. Sci Total Environ. 2020;728:138860. doi:10.1016/j.scitotenv.2020.138860
49. Sun C, Wu Q, Zhang C. Managing patients with COVID-19 infections: a first-hand experience from the Wuhan Mobile Cabin Hospital. Br J Gen Pract. 2020;70(694):229–230. doi:10.3399/bjgp20X709529
50. Chakraborty T, Ghosh I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Soliton Fract. 2020;135:109850. doi:10.1016/j.chaos.2020.109850
51. Singh S, Parmar KS, Kumar J, Makkhan SJS. Development of new hybrid model of discrete wavelet decomposition and Autoregressive Integrated Moving Average (ARIMA) models in application to one month forecast the casualties cases of COVID-19. Chaos Soliton Fract. 2020;135:109866. doi:10.1016/j.chaos.2020.109866
 © 2020 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2020 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.