Back to Journals » International Journal of Women's Health » Volume 10
Dimensional analysis of the endometrial cavity: how many dimensions should the ideal intrauterine device or system have?
Authors Goldstuck ND
Received 28 November 2017
Accepted for publication 22 February 2018
Published 9 April 2018 Volume 2018:10 Pages 165—168
DOI https://doi.org/10.2147/IJWH.S158281
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Elie Al-Chaer
Norman D Goldstuck
Department of Obstetrics and Gynecology, Faculty of Medicine and Health Sciences, Stellenbosch University and Tygerberg Hospital, Bellville, Western Cape, South Africa
Background: The geometrical shape of the human uterus most closely approximates that of a prolate ellipsoid. The endometrial cavity itself is more likely to also have the shape of a prolate ellipsoid especially when the extension of the cervix is omitted. Using this information and known endometrial cavity volumes and lateral and vertical dimensions, it is possible to calculate the anteroposterior (AP) dimensions and get a complete evaluation of all possible dimensions of the endometrial cavity. These are singular observations and not part of any other study.
Methods: The AP dimensions of the endometrial cavity of the uterus were calculated using the formula for the volume of the prolate ellipsoid to complete a three-dimensional picture of the endometrial cavity.
Results: Calculations confirm ultrasound imaging which shows large variations in cavity size and shape. Known cavity volumes and length and breadth measurements indicate that the AP diameter may vary from 6.29 to 38.2 mm. These measurements confirm the difficulty of getting a fixed-frame intrauterine device (IUD) to accommodate to a space of highly variable dimensions. This is especially true of three-dimension IUDs. A one-dimensional frameless IUD is most likely to be able to conform to this highly variable space and shape.
Conclusion: The endometrial cavity may assume many varied prolate ellipsoid configurations where one or more measurements may be too small to accommodate standard IUDs. A one-dimensional device is most likely to be able to be accommodated by most uterine cavities as compared to two- and three-dimensional devices.
Keywords: intrauterine device, dimensions, endometrial cavity, prolate ellipsoid, variable space and shape
Introduction
The first clinically used intrauterine devices (IUDs) were introduced by Richter and Pust and later Grafenberg in Germany.1–3 All three made IUDs using the material which was available at the time. These materials were rigid and difficult to insert and their geometrical shape would have caused significant to extreme distortion of the endometrial cavity. This was naturally accompanied by pain, bleeding, and discomfort, and even infection.
The plastics revolution of the 1950s helped Lippes design the Lippes Loop IUD which was made of polyethylene impregnated with barium sulfate. It was malleable and would retain its shape and could be withdrawn into an inserter tube and injected into the endometrial cavity where it would resume its original shape.4 It worked because it had a surface area of at least 600 mm2, which is about the surface area that plastic only IUDs require to be effective.5 The Loop came in four sizes which were crudely based on the uterine dimensions reported in Dickinson’s book on human sexual anatomy. These dimensions are too large for the dynamic uterine cavity in vivo. Although the insertion procedure was much more tolerable than that of the earlier devices, the experience during subsequent usage was still problematical due to distortion of the uterine cavity by the oversized loops. This was true even of the smallest size. The extent of this IUD-induced increase in menstrual blood loss (MBL) appears to be related to the size of the device. The greater the size of the device, the greater the amount of MBL. The Lippes Loop, one of the larger IUDs developed, has been shown to result in an increase of up to 140% in MBL during the first year after insertion.6 In the late 1960s, the antifertility effect of copper was discovered by Chang at the Worcester Institute in Massachusetts. Its antifertility effect was exploited for use as an intrauterine contraceptive by attaching it to a “7” shaped plastic frame (Zipper) or a “T” shaped plastic frame (Tatum). The anatomical basis for the shape and size of these frames was Dickinson’s work.7 With hindsight and the benefit of modern high-resolution ultrasound, we now know that the original size of most of these plastic frames was too large.8,9 More surprising is that these original sizes have gone largely unaltered in the light of this new evidence.8
A frame is like a skeleton – it gives stability and the ability to withstand collapsing and gravitational forces, which is why vertebrates have them. Invertebrates, like the octopus, do not have skeletons (frames) and cannot withstand these forces but can resist compressive forces by molding their bodies to fit very small and changing spaces. In order to successfully occupy a hollow muscular organ like the uterus, an IUD does not need to be able to resist collapsing and gravitational forces – it needs to be able to adapt to small liquid potential spaces. An IUD needs to be able to fit and adapt to these small liquid filled spaces which are continually changing with uterine muscular activity and contractions. Ideally, it needs to be able to mold and change its shape effortlessly to that of the endometrial cavity; in other words, it ideally really needs to be frameless and without a skeleton. Just how small and changeable is the endometrial cavity?
Methods
The uterus itself most closely approximates the geometrical shape of a prolate ellipsoid.10 The endometrial cavity is a hollowed-out space which appears to be fairly symmetrical within the uterus itself. Additionally, since we can eliminate the cervix and the cervical canal (which are not part of the endometrial cavity), the endometrial cavity itself can be assumed to also take the shape of a prolate ellipsoid, and in fact removal of the cervix ensures that the cavity more closely approximates a prolate ellipsoid than does the whole uterus. The volume of a prolate ellipsoid is given by the following formula:
|
where V = volume of the endometrial cavity (mL)
π~3.14
L = length (fundus to internal os of endometrial cavity)
W = width (between cornual ostia of endometrial cavity)
and AP = anteroposterior diameter of the endometrial cavity perpendicular to L.
Endometrial cavity volume has been measured and varies between 5 and 10 mL.11
Transfundal endometrial cavity width varies widely from as little as 7 mm in very narrow cavities to the more usual 22–34 mm depending on parity. There is a wide variation in uterine measurements, but it is possible to calculate boundary values which will accommodate most sizes and volumes.
Results
Table 1 gives representative values for a range of volumes and for a range of endometrial cavity widths and lengths. It was obtained by using extreme values of volume and lateral longitudinal uterine cavity measurements to calculate AP dimensions using the prolate ellipsoid formula given in the previous section. For example, in a low-volume endometrial cavity of length 40 mm and width 38 mm, the equation shows that the AP diameter would be 6 mm.
During uterine contraction, the endometrial cavity is distorted even further, which can reduce the value of these dimensions. An IUD which has 2 or 3 dimensions needs a large enough size to anchor but should not be so large as to cause problems.12 A one-dimensional IUD cannot form a dimensional anchor and needs to be tethered to the uterine wall if it is to remain in place, eg, Gynefix.12
Discussion
The external longitudinal and internal circular muscle fibers of the uterus are a continuation of the tubal muscle fibers. In addition, there are circular fibers which sweep around the uterus in both clockwise and counterclockwise directions.7 Uterine muscular contractions sweep down through the myometrium from the fundus to the cervix. This arrangement of the muscle fibers means that the endometrial cavity dimensions will change in all three axes (L, W, AP), ie, there will be three-dimensional change in the endometrial cavity.
While not all IUD-related problems are related to dimensional incompatibility between the IUD and the endometrial cavity, it is likely that mismatch between the size of the IUD and the uterine cavity is certainly not optimal and can only be detrimental to device performance.9 It follows logically therefore that the greater the number of dimensions an IUD has, the greater the chance it has of being incompatible with the endometrial cavity in one of its three dimensions. This is because it would have to be compatible with the length, width, and AP diameter of the endometrial cavity. Figure 1 shows a severely distorted uterine cavity due to a manifest discrepancy between the IUD and the endometrial cavity.
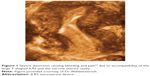  | Figure 1 Severe distortion causing bleeding and pain13 due to incompatibility of the large T-shaped IUD and the narrow uterine cavity. |
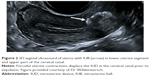
This also explains why the “Intrauterine ball,” a three-dimensional device with a flexible nitinol frame has been associated with expulsion problems (Figure 2).14
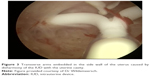
Our previous models have only examined static two-dimensional changes. While it is difficult for framed devices to accommodate to changing lateral (and sometimes linear) dimensions, it is virtually impossible for them to simultaneously adapt to changing AP dimensions as well, since they would be subject to changes of force in three dimensions. This produces a three-dimensional squeeze which, at worst, is possibly responsible for secondary perforation15 but leads to the user experiencing pain and discomfort, often accompanied by embedment (Figure 3).
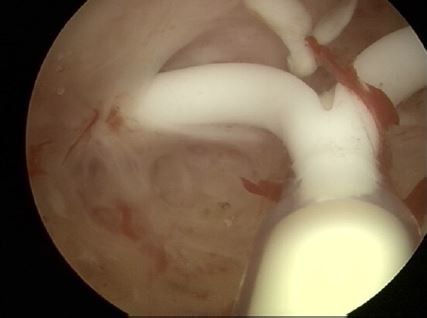
Only a frameless IUD which behaves analogously to an invertebrate can adapt to the changing and very small spaces in an “octopus-like” manner. Thus, it is able to adapt to sit comfortably in low-volume, flexed, and/or distorted endometrial cavities (Figure 4). A multicenter study found a maximal cavity width <20 mm in 32% of nulliparous women. Due to the small volume of the frameless IUD, the impact on amount of MBL is also minimal.16
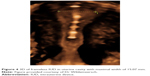  | Figure 4 3D of frameless IUD in uterine cavity with maximal width of 15.07 mm. |
Conclusion
There are two main limitations to the dimensional approach toward IUD design. First, the size of the endometrial cavity is very variable, so an IUD of any one size is not able to fit a wide range of cavities. Second, the uterus will sometimes show tolerance to what appear to be ill-fitting devices. The problem of one-dimensional IUDs is that presently they are anchored by “harpooning” into the myometrium. This technique requires insertion training and is tissue invasive.15 However, proficiency is easily acquired for those who are skilled IUD providers. Evidently, a one-dimensional frameless IUD that is self-adherent to the endometrial cavity would appear to be optimal, but this may not be technically feasible.
Disclosure
The author reports no conflicts of interest in this work.
References
Richter R. Ein Mittal zur Verhuetung der Konzeption. Deutsch Med Wschr. 1909;35:1525–1527. | ||
Pust K. Einbreichbarer Frauenschutz. Deutsch Med Wschr. 1923;49:952–953. | ||
Grafenberg E. Silk as anticoncipient. In Bendix K, editor. Geborten Regelung – Vortraege und Verhandlung en des Aerztekursus vom 28–30 Dezember 1928. Berlin: Selbsverlag; 1929. | ||
Lippes J. Contraception with intrauterine plastic loops. Am J Obstet Gynecol. 1965;93(7):1024–1030. | ||
Moyer DL, Mishell DR. Reactions of human endometrium to the intrauterine foreign body. II. Long term effects on the endometrial histology and cytology. Am J Obstet Gynecol. 1971;111:66–80. | ||
Milsom I, Andersson K, Jonasson K, et al. The influence of the Gyne-T 380S IUD on menstrual blood loss and iron status. Contraception. 1995;52:175–179. | ||
Dickinson RL. Human Sex Anatomy. Huntington, NY: Robert E. Krieger Publishing Co.; 1971. | ||
Wildemeersch D, Pett A, Jandi S, Hasskamp T, Rowe P, Vrijens M. Precision intrauterine contraception may significantly increase continuation of use: a review of long-term clinical experience with frameless copper-releasing intrauterine contraception devices. Int J Women’s Health. 2013;5:215–225. | ||
Goldstuck ND. The relationship of IUD dimensions to event rates. Contracept Deliv Syst. 1982;3:103–105. | ||
Das S, Sheth S. Uterine volume: an aid to determine the route and technique of hysterectomy. J Obstet Gynecol Ind. 2004;54(1):68–74. | ||
Shild RL, Indefrei D, Eschweiler S, van der Ven H, Fimmers R, Hansmann M. Three-dimensional endometrial volume calculation and pregnancy rate in an in-vitro fertilization programme. Hum Reprod. 1999;14(5):1255–1258. | ||
Goldstuck ND, Wildemeersch D. Prevention of intrauterine device expulsion and intolerance: determination of the anchor mechanism. Clin Obstet Gynecol Reprod Med. 2017;3(1):1–8. | ||
Wildemeersch D, Rowe PJ. Assessment of menstrual blood loss in Belgian users of the frameless copper-releasing IUD with copper surface are of 200 mm2 and users of a copper-levonorgestrel-releasing intrauterine system. Contraception. 2004;70:169–172. | ||
Wiebe E, Trussell J. Discontinuation rates and acceptability during 1 year of using the intrauterine ball (the SCu380A). Contraception. 2016;93:364–366. | ||
Goldstuck ND, Wildemeesch D. Role of uterine forces in intrauterine device embedment, perforation, and expulsion. Int J Womens Health. 2014;6:735–744. | ||
Wildemeersch D, Hasskamp T, Nolte K, et al. A multicenter study assessing uterine cavity width in over 400 nulliparous women seeking IUD insertion using 2D and 3D sonography. Eur J Obstet Gynecol Reprod Biol. 2016;206:232–238. |
 © 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.