Back to Journals » Research and Reports in Urology » Volume 7
Verification of relationships between anthropometric variables among ureteral stents recipients and ureteric lengths: a challenge for Vitruvian-da Vinci theory
Authors Acelam P
Received 3 May 2015
Accepted for publication 8 July 2015
Published 13 August 2015 Volume 2015:7 Pages 117—124
DOI https://doi.org/10.2147/RRU.S87860
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Jan Colli
Philip A Acelam
Walden University, College of Health Sciences, Minneapolis, MN, USA
Objective: To determine and verify how anthropometric variables correlate to ureteric lengths and how well statistical models approximate the actual ureteric lengths.
Materials and methods: In this work, 129 charts of endourological patients (71 females and 58 males) were studied retrospectively. Data were gathered from various research centers from North and South America. Continuous data were studied using descriptive statistics. Anthropometric variables (age, body surface area, body weight, obesity, and stature) were utilized as predictors of ureteric lengths. Linear regressions and correlations were used for studying relationships between the predictors and the outcome variables (ureteric lengths); P-value was set at 0.05. To assess how well statistical models were capable of predicting the actual ureteric lengths, percentages (or ratios of matched to mismatched results) were employed.
Results: The results of the study show that anthropometric variables do not correlate well to ureteric lengths. Statistical models can partially estimate ureteric lengths. Out of the five anthropometric variables studied, three of them: body frame, stature, and weight, each with a P<0.0001, were significant. Two of the variables: age (R2=0.01; P=0.20) and obesity (R2=0.03; P=0.06), were found to be poor estimators of ureteric lengths. None of the predictors reached the expected (match:above:below) ratio of 1:0:0 to qualify as reliable predictors of ureteric lengths.
Conclusion: There is not sufficient evidence to conclude that anthropometric variables can reliably predict ureteric lengths. These variables appear to lack adequate specificity as they failed to reach the expected (match:above:below) ratio of 1:0:0. Consequently, selections of ureteral stents continue to remain a challenge. However, height (R2=0.68) with the (match:above:below) ratio of 3:3:4 appears suited for use as estimator, but on the basis of decision rule. Additional research is recommended for stent improvements and ureteric length determinations.
Keywords: anthropometry, uropathy, ureteral stents, ureteric lengths, Vitruvian theory
Introduction
In the late 1960s, the pioneers of ureteral stents had defined the devices as tubes that are inserted either in a retrograde or antegrade manner inside abnormally functioning ureters to maintain patency.1,2 Today, ureteral stents have become indispensable medical devices in managing urinary obstructions.3 It is estimated that over 1.5 million stents are inserted annually in the United States.4 A prior study concluded that ureteral stents may be over used.5
Increased use of ureteral stents has resulted in increased numbers of complications associated with them.4,6,7 For instance, after insertion of the instruments, urinary blockages may occur 25% of the time due to biofilm (encrustation) formation; approximately 11% of the time, stents may slip off, especially if abnormally short sizes are fitted.8,9 Hydronephrosis occurs in approximately 7% of cases.10 Problems associated with ureteral stents are significant and are – or should be – of concern.
When a ureteral stent slips off its intended position in the ureter, it causes discomfort for the patient.7,9 To prevent this complication, stents of the correct dimensions must be selected.8,11 Length determinations have become important parts of ureteral stent insertion.9 However, currently, there is still no standardized method to determine ureteric lengths.9,12,13 Efforts to address the problem are ongoing. A number of methods have been proposed including the use of anthropometric variables based on the Vitruvian-da Vinci theory. Surprisingly, the answers obtained through those methods are unpredictable. A previous study concluded that during endoscopic procedures, the measurement of individuals’ anthropometric variables, such as stature, does not correlate well with the appropriate lengths of ureteral stents.11 Another study even questioned the validity of using individuals’ anthropometric variables as predictors of the lengths of ureteral stents.14
In studying the associations between ureteral stents and anthropometric variables, I noticed that previous research used homogeneous study populations.11,15–19 This raises concerns about the generalizability of those results. To my knowledge, none of the previous studies used diverse populations in their work, and none of them have conducted observational (experimental) trials in order to compare and verify how well their proposed models can predict or approximate the actual lengths of the ureters.20
The objectives of this study were to determine how well anthropometric variables such as stature, age, body weight, body surface areas, and degree of obesity correlate to ureteric lengths, and to see how well the results of statistical models match or mismatch the actual lengths of the ureters.16,20,21 To acquire a diverse study population, people in North and South America were considered ideal because the two continents include descendants of Africans, Asians, Europeans, and Native Americans. Data were obtained from urological centers and hospitals from Argentina, Brazil, Canada, Costa Rica, Mexico, and the United States of America.
Materials and methods
This was a data-oriented type of research. No human participants were directly involved in the study. As such, institutional review was not sought. The study used retrospective data obtained by contacting a number of urological centers and hospitals with internationally recognized credentials (eg, teaching hospitals) from many countries as mentioned above. Contacts of potential sources were obtained from hospital guides. Sources of the data were primary researchers who (in some cases) had tried to carry out similar studies, but could not get enough data and had abandoned the work. When contacted, the researchers were generous enough to share their data. The data were collected and rechecked for accuracy and processed for analysis.
Modes of communications were through telephone and/or email. The nature of the study and the rights to decline were explained to the potential parties. Questionnaires were then sent to those parties who agreed to perform retrospective reviews of their records and share their data. After answering the questionnaires, the respondents returned them via email. This strategy presented a few problems, such as it was very time consuming, and lasted for approximately 3 years (October 2011–November 2014). Secondly, there were language barriers. Some of the respondents answered their questionnaires in languages other than English, in which cases I had to rely on translators. Thirdly, the respondents used different units to report results. For example, only 38% (40/129) of the respondents used the metric system (kilograms, meters, centimeters, and millimeters). Sixty-two percent of the respondents (80/129) used the British/American units (pounds, yards, feet, and inches). For that reason, it seemed reasonable to adopt both the metric system and the British/American units in this paper. Fourth, there were differences in the way respondents reported ages. Some used whole numbers, while others included fractions or decimals when reporting ages. For example, a patient who was 20 years and 6 months of age was reported to be 20.5 years old. To avoid working with fractions and rounding off decimals, I decided to present all ages in months. For the same reason, measurements of the heights of subjects and ureteric lengths are presented in inches as well. Individuals’ body weights are reported in pounds (and kilograms).
An individual’s total body size and his/her degree of obesity were derived from anthropometric measures.22 Body frame was computed and is presented in this paper as surface body area (sBA measured in in2). The computations were performed using the method provided in DuBois and DuBois23 and Mostellar.24 Degree of obesity was calculated and presented using the body mass index (BMI measured in lbs/in2). These calculations were performed using the method provided by the Centers for Disease Control (CDC).
Respondents also used different methods to measure ureteric lengths. Forty-seven percent (60/129) stated that they used traditional intravenous urography. Thirty percent (39/129) reported using axial computerized tomographic techniques, and 23% (30/129) reported using either catheterization or other methods. The kind of stent that was inserted most frequently was the double pigtails type.
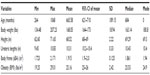
As shown in Tables 1 and 2, the study included the records of 129 patients (71 females; 58 males) who had sought urological care in various centers in North and South America. The data were subjected to statistical and graphical analyses. Continuous data were analyzed using descriptive statistics. Regressions and correlations were used to study the relationships between the variables, and P-value was set at 0.05.
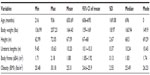  | Table 2 Descriptive statistics of the 58 males included in the study |
Inclusion/exclusion criteria
Each questionnaire sought specific pieces of information, including demographic data for each patient, the chief complaint for which the patient had sought care, the method used for measurements (eg, ultrasonography, traditional intravenous urography, computed tomography urography, 5-Fr ureteral catheterization, guidewire, etc), any noticeable defects in the kidneys and/or ureters, any evidence of sepsis and/or infectious diseases, and the type of stent inserted.
To be included in the study, data sets must have been collected from a verifiable hospital or a urological center under the guidance of, at least, a physician; and the record had to be from a patient who had sought care for urological problems that required stent insertion. Further, at the time when care was provided, the patient had to be an adult (ie, at least 18 years of age or older). Finally, the practitioners had to have used the right method(s) of measurements showing clear units.
There were two guiding definitions. Ureteric length was defined as the continuous distance between the ureteropelvic and ureterovesicular points. Stature was defined as the continuous distance from the heels upwards to the apex, measured while the same individual was standing with his/her back against an upright tape measure.
Results
Results of the continuous data showed that females were 22 to 89 years of age, with a mean age of 55.4 years (Table 1). Their weights ranged from 134.48 lbs (61.13 kg) to 207.23 lbs (94.2 kg). They were of medium height (ranging from 5 feet 2 in [157 cm] to 6 feet 0 in [183 cm]). The lengths of the ureters for the women ranged from 9.45 in (24 cm) to 10.83 in (27.6 cm). The women had small body frames, although some of them could be described as obese according to the CDC standards (BMI >25.0).
The male subjects ranged in ages from 18 to 78 years (Table 2). Their weights ranged from 136.69 lbs (62.30 kg) to 207.23 lbs (94.2 kg). For the males, the shortest height was 5 feet 2 in (160 cm) and the tallest was 6 feet 0 in (183 cm). The remainder of the measurements was also similar to those carried out in women, as shown in Table 1.
For the anthropometric variables, the results showed that three of the variables were statistically significant (Table 3). The scatter plot for body surface area versus ureteric length is shown in Figure 1. As shown in Table 3, the results of body surface area had a correlation coefficient (r) of 0.55 and a correlation of determination (R2) of 0.30 (P<0.0001; 95% CI [confidence interval] =0.41–0.66). The results of the experimental trial, shown in Table 4, show that the regression model for body surface area versus ureteric length was able to predict the reported actual ureteric lengths only 12.4% (16/129) of the time.
  | Figure 1 Scatter plot depicting a weak positive association between body frame (quantified as body surface area in square inches) and ureteric lengths (inches) for the entire study population. |
Second, the scatter plot for ureteric length versus body weight (lbs) is shown in Figure 2. The graph of body weight versus ureteric lengths indicates that the variable had a r of 0.40 and a R2 of 0.16 (P<0.0001; 95% CI =0.24–0.53) (Table 3). The results of the experimental trials of the models, shown in Table 4, indicate that body weight predicted the reported actual lengths of the ureters 9.3% (12/129) of the time.
  | Figure 2 Scatter plot showing a weak positive association between ureteric lengths (inches) versus weight (lbs). |
Third, the scatter plot for ureteric length and height is as shown in Figure 3. The curve of the association between the two variables showed a r of 0.83 and a R2 of 0.68 (P<0.0001; 95% CI =0.76–0.87). This is shown in Table 3. Using the regression model for the experimental trial, the variable of height predicted 24.8% (32/129) of the reported actual ureteric length correctly (Table 4).
Again, as can be seen from Table 3, the results of the two remaining anthropometric variables, age and obesity, were not significant (P>0.05). Also, both variables showed low percentage of correct ureteric length predictions (Table 4).
Discussion
To give a bit of background here, Vitruvian-da Vinci theory has held the view that there is consistent proportionality in the physical attributes of a normal human.20,25,26 The artists (as well as the architects) used the simplified version of the theory and argued that since proportionality exists, human figures could be drawn using simple geometrical representations such as rectangles and circles.27 Practitioners of the art of healing have held that proportionality of the normal human body does exist, but they [practitioners] argued that such proportionality gets disrupted in the presence of certain illnesses (eg, spinal deformity, physical structural malformations, and in respiratory or lungs abnormalities).28–31 In other words, the absence of proportionality in humans may be the basis for suspecting the presence of certain health conditions.
However, in the past 200 years, standardized methods of measurements began to emerge.28 With the results obtained through better methods of measurements, researchers began to question the validity of some of the suppositions or the artists’ simplified concepts of pictorial representations based on Vitruvian-da Vinci theory.28 As a result, doubts about the reliability of Vitruvian-da Vinci theory began to emerge too. To understand reliability or validity of Vitruvian-da Vinci theory, researchers have continued to investigate, for example, the relationships between arm span and stature.20,32 There have been reports that arm span did exceed heights, even among normal individuals, although in some cases, arm spans were found to equal height.20 Bonomi20 also studied the relationship between arm span and stature. He had a reasonable sample size (N=84).28 The results of Bonomi’s work showed that arm span matched height only 7% (6/84) of the time, while it fell below height 29% (24/84) of the time, and exceeded height 64% (54/84) of the time.28 In the form of a ratio, Bonomi’s20 results may be summarized as 1:6:3 (matched:above:below). Arguably, if arm span could reliably predict height, then the results of the study would have been in the ratio of 1:0:0 (matched:above:below).
Since Bonomi’s work,20 a number of investigators have come to the same conclusion that arm span does exceed height, even among normal individuals.26,28,31 Thus far, the results of those studies have challenged the reliability of the Vitruvian-da Vinci theory of proportionality in the normal human body.9,12,25
In this study, I used retrospective data and relied on regression models to verify anthropometric variables (as predictors) versus ureteric lengths (as outcome). From Table 4, it can be seen that whether measures of anthropometric variables against ureteric lengths are taken individually or collectively, the ratio of the results categorized as “matched:above:below” is/are still not in the form of 1:0:0. The results appear to suggest that no anthropometric variables are able to predict ureteric lengths reliably.13,17,18,20,33 However, the anthropometric variable of height may continue to be used to predict or approximate ureteric lengths, but the reliability and/or validity of the variable remains questionable.17,34
Despite the belief that there may be a relationship between ureteric lengths and anthropometric measures, a number of researchers who have tried to verify such a relationship have reported negative findings.11,19,26,27,35 Some studies challenged the validity of using individuals’ anthropometric variables as predictors of the lengths of ureteral stents.14,18,34 Hruby et al18 reported that they were unable to find any strong correlations between anthropometric measures and ureteric lengths. Also, in the study where researchers evaluated lengths of ureters in adult cadavers in a Brazilian population, the authors reported finding no correlations between the two variables.20
In contrast, some researchers have reported finding correlations between anthropometrics and ureteric lengths. Ho et al15 reported finding a correlation between anthropometric variables and ureteric lengths among the Chinese population. Lee et al33 also reported finding similar correlations among Korean populations. Further, similar correlations were reported among the Japanese populations.17 However, as in some of the previous studies,13,14,18 Kawahara et al17 also questioned the validity/reliability of using such a correlation to predict ureteric length. Notably, among the studies that reported finding correlations between height and ureteric lengths, none has reported the categorized ratio of the variables as “matched:above:below”.20
Statistically, correlations describe associations between random variables and do not reflect causal relationships. For example, the results presented in Figure 1 show a weak positive association between ureteric length and body surface area. Likewise, Figure 2 shows a weak positive association between ureteric length and body weight. In those two results, both body surface area and body weight are measures that reflect growth. The growth may be in the form of parenchymal cells that lead to changes in axial or linear dimensions of the ureters.22 Thus, changes in growth of the body may be reflected in the ureters, causing dilatation that results in what researchers have referred to as a “megaureter”.36,37 Nonetheless, based on the data used in this study, variables such as body surface area and/or body weight do not appear suitable for predicting ureteric lengths.
Obesity is growth of another kind. Figure 4 shows a diminishing association between ureteric length and obesity, which was quantified as BMI. This is another way of saying that obesity is a measure of adiposity. As can be seen from the scatter plot in Figure 4, obesity is also not well suited as a variable to predict ureteric length.
Just as in Figure 4, Figure 5 also shows a diminishing association between ureteric lengths and age (months). Notably, the slope of the line in Figure 5 is near zero, thus suggesting that the association between the two variables, if any, is negligible. Given that limitation, age also may not be used as a predictor of ureteric length.
A statistical authority pointed out that in linear regression, one of the variables (say Y) is considered to be random, while the other (say X) is fixed.38 In a correlation study, on the other hand, both variables Y and X are considered to be random.38 In view of that, it does seem reasonable to infer that correlations or associations between anthropometric variables and ureteric lengths may be interpreted as random events that seem to vary together. This type of phenomenon is commonly seen where Vitruvian-da Vinci theory is applied.20 The results of the experimental trials shown in Table 4 appear to confirm that. That is, there are times when a variable may show matching results. The results of this study seem to agree with the findings reported in a number of previous studies.11,13,14,18,20
In the experimental trials, the results shown in Table 4 that were considered a “match” could be interpreted as the consequences of random events, in that it is possible for people of a certain stature to have identical (or almost identical) ureteric lengths. However, that fact alone does not mean that one of the variables may be predicted by the other.38 This is so because it is possible that there is a broader range of variations in stature among individuals than can be accounted for by ureteric lengths.18 One reason for saying so is that there is no cause and effect in this type of relationship.38 Tall individuals may have long ureteric lengths, and short people may have short ureteric lengths, but based on those observations alone, it is difficult (if not impossible) to make accurate predictions of ureteric length using an individual’s height or another form of anthropometric variable.18 A previous study reported, what they found in their study of a Brazilian population, that even some tall individuals have shorter than expected ureteric lengths.13
One may be tempted to use an individual’s stature to approximate ureteric length on the basis of decision rule, and that may be acceptable.39 However, the distinction to be made clear is that approximations are not accurate/reliable predictions. In endourology, accurate predictions of ureteric length are necessary in order to determine the ideal length (or comfortable range) of indwelling stents.11 By relying on approximations, one is more likely than not to select a ureteral stent that is either too long or too short for a particular purpose. It is perhaps needless to add that inserting indwelling stents of improper lengths may not be comfortable or beneficial to the patients who need them.7,40
Recommendation
A common form of discomfort for this group of patients is associated with the insertion of stents of improper sizes. It is important to fit stents of the right size (and of the right material), and thus far, the practice of estimating the lengths of stents to be inserted has been based on anthropometric variables (eg, heights) of the patients. More often than not, this type of approximation has led to the insertion of stents that are either too long or too short, both of which increase a patient’s discomfort, pain, morbidity, or other complications. The reliability of height as a variable for predicting ureteric lengths continues to be debatable.11,19 Height can continue to be used on the basis of decision rule, especially if reliable cutoff points could be developed.39 That, however, requires standardization.13,17 Therefore, it is recommended that further work be directed at finding ways to standardize ureteral measurements.13,17 The idea of using a statistical formula to predict the actual lengths of the ureters is appealing because it is a radiation-free procedure.16 Apparently, what needs to be done is to find reliable conversion factors that may be used with statistical models.
Limitations
The first limitation of the study is that I used retrospective data on events that were provided by primary sources. This may raise two concerns. First, it is possible that some of the information about the variables might be questionable or that some of the data were measured in ways that could be interpreted as inappropriate.19 I had no way of knowing and correcting those types of anomalies (if they existed). Secondly, there was no way of proving that the grading of the final stent position or the predicted lengths fell within an acceptable range that did not cause the patients discomfort. This study method was adopted because it is an economical way of obtaining data from a diverse population. Although it did not directly involve human participants, the strength of the study includes its ability to pinpoint the limitations of some of the anthropometric variables that have been used to measure ureteric lengths.
Conclusion
The five anthropometric variables appear to be generic in the sense that they lack adequate specificity for predicting ureteric lengths. I was unable to find adequate evidence to conclude that any of the five anthropometric variables correlate well with ureteric lengths or are reliable enough for predicting ureteric lengths. Although statistical models can approximate, and in some cases predict, the length of the ureters, more work is necessary in order to achieve the strength of mathematical models for application to the reliable prediction of the actual lengths (or range of lengths of stents) acceptable for patients. Ways of addressing these patients’ discomfort, pain, and complications appear to include standardizing the methods of selecting the lengths of indwelling ureteral stents.
Acknowledgement
Philip A Acelam thanks all the parties who provided the necessary data sets for this study.
Disclosure
This study was neither supported nor funded by any source. The author reports no conflicts of interest in this work.
References
Zimskind PD, Fetter TR, Wilkerson JL. Clinical use of long-term indwelling silicone rubber ureteral splints inserted cystoscopically. J Urol. 1967;97:840–844. Available from: http://www.ncbi.nlm.nih.gov/pubmed/6025928. | |
Yossepowitch O, Lifshitz DA, Dekel, Y, et al. Predicting the success of retrograde stenting for managing ureteral obstruction. J Urol. 2001; 1746–1749. doi: http://dx.doi.org/10.1016/S0022-5347(05)65666-2. | |
Marmar JL. The management of ureteral obstruction with silicone rubber splint catheters. J Urol. 1970;104:386–389. Available from: http://www.ncbi.nlm.nih.gov/pubmed/5459972. | |
Chew BH, Knudsen BH, Denstedt D. The use of stents in contemporary urology. Curr Opin Urol. 2004;14:111–115. Available from: http://www.ncbi.nlm.gov/pubmed/15075840. | |
Auge BK, Sarvis JA, L’Esperance JO, Preminger G. Practice patterns of ureteral stenting after routine ureteroscopic stone surgery: a survey of practicing urologists. J Endourol. 2007;21:1287–1291. | |
Joshi HB, Stainthorpe A, Macdonagh RP, Keeley FX Jr, Timoney AG, Barry MJ. Indwelling ureteral stents: evaluation of symptoms, quality of life and utility. J Urol. 2003;169(3):1065–1069. | |
Rane A, Saleemi A, Cahill D, Sriprasad S, Shrotri N, Tiptaft R. Have stent-related symptoms anything to do with placement technique? J Endourol. 2001;15:741–745. | |
Breau RH, Norman RW. Optimal prevention and management of proximal ureteral migration and remigration. J Urol. 2001;166:890–893. | |
Slaton JW, Kropp, KA. Proximal ureteral stent migration: an avoidable complications? J Urol. 1996;155:58–61. doi: http://dx.doi.org/10.1016/S0022-5347(01)66539-X. | |
Mokhmalji H, Braun PM, Martinez-Portillo FJ, Siegsmund M, Alken P, Kohrmann KU. Percutaneous nephrostomy versus ureteral stents for diversion of hydronephrosis caused by stones: a prospective, randomized clinical trial. J Urol. 2001;165(4):1088–1092. | |
Jeon SS, Choi YS, Hong JH. Determination of ideal stent length for endourologic surgery. J Endourol. 2007;21:906–910. | |
Pilcher JM, Patel U. Choosing the correct length of ureteric stent: a formula based on the patient’s height compared with direct ureteric measurement. Clin Radiol. 2002;57:59–62. | |
Noaves HF, Leite PC, Almeida RA, et al. Analysis of ureteral length in adult cadaver. Int Braz J Urol. 2013;39(2):248–256. | |
Shah J, Kulkarni RP. Height does not predict ureteric length. Clin Radiol. 2005;60:812–814. | |
Ho CH, Huang KH, Chen SC, Pu YS, Liu SP, Yu HJ. Choosing the ideal length of a double-pigtail ureteral stent according to body height: study based on a Chinese population. Urol Int. 2009;83:70–74. | |
Bozzini G, Cassallato S, Vigano A, et al. Predicting female ureteral length: a mathematical model. J Clin Urol. 2014;7:4266–4271. | |
Kawahara T, Ito H, Terao H, et al. Which is the best method to estimate the actual ureteral length in patients undergoing ureteral stent placement. Int J Urol. 2012;19:634–638. | |
Hruby GW, Ames CD, Yan Y, Monga M, Landman J. Correlation of ureteric length with anthropometric variables of surface body habitus. Br J Urol Int. 2007;99:1119–1122. | |
Lee C, Kuskowski M, Premoli J, Skemp N, Monga M. Randomized evaluation of ureteral stents using validated symptoms questionnaire. J Endourol. 2005;19:990–993. | |
Bonomi J. The Proportion of Human Figure. 5th ed. London, UK: Charles Robertson; 1880. | |
Hao P, Li W, Song C, Yan J, Song B, Li L. Clinical evaluation of double-pigtail in patients with upper urinary tract diseases: report of 2685 cases. J Endourol. 2008;22(1):65–70. | |
Pfister RC, Hendren WH. Primary megaureter in children and adults. Clinical and pathophysiologic features of 150 ureters. Urology. 1978;12(2):160–176. Available from: http://dx.doi.org/10.1016/0090-4295(78)90327-8. | |
Du Bois D, Du Bois EF. A formula to estimate the approximate surface area if height and weight be known. 1916. Nutrition. 1989;5:303–311; discussion. Available from: http://www.ncbi.nlm.nih.gov/pubmed/2520314. | |
Mostellar RD. Simplified calculation of body surface area. N Engl J Med. 1987;317(17):1098. | |
Schott GD. The extent of man from Vitruvius to Marfan. Lancet. 1992;340:1518–1520. | |
Pearson K, Lee A. On the laws of inheritance of man. Biometrika. 1902;2:357–461. | |
Panosky E. Meaning in the Visual Arts. Harmondsworth, UK: Peregrine; 1970. | |
Aggarwal AN, Gupta D, Ezekiel LM, Jindal SK. Statistical estimation of heights from arm span in North Indian subjects. Indian J Physiol Pharmacol. 2000;44(3):329–334. Available from: http://www.ijpp.com/IJPP%20archives/2000_44_3/329-334.pdf. | |
Hilbert NE, Lanigan A, Raven J, Phelan P. Relationship to arm span and the prediction of lung function. Thorax. 1988;43:657–659. | |
Parker JM, Dillard TA, Phillips YY. Arm span height relationship in patients referred for Spirometry. Am J Respir Crit Care Med. 1996;154:533–536. | |
Sinclair RJG, Kitchin AH, Turner RWD. The Marfan syndrome. Q J Med. 1960;29:19–46. | |
Zverev YP. Relationship between arm span and stature in Malawian adults. Ann Hum Biol. 2003;30:739–743. | |
Lee BK, Paick SH, Park HK, Kim HG, Lho YS. Is a 22 cm ureteric stent appropriate for Korean patients smaller than 175 cm in height? Korean J Urol. 2010;51:642–646. | |
Wong JY, Oh AK, Ohta E, et al. Validity and reliability of craniofacial anthropometric measurement of 3D digital photogrammetric images. Cleft Palate Craniofac J. 2008;45:232–239. | |
Palmer JS, Palmer LS. A simple and reliable formula for determining the proper JJ stent length in the pediatric patient: age + 10. Urology. 2007;70:264. | |
Hemal AK, Ansari MS, Doddamani D, et al. Symptomatic and complicated adult and adolescent primary obstructive megaureter – indications for surgery: analysis, outcome, and follow-up. Urology. 2003;61(4):703–707. | |
King LR. Megaloureter: definition, diagnosis and management. J Urol. 1980;123(2):222–223. Available from: http://www.ncbi.nlm.nih.gov/pubmed/7354523. | |
Altman DG. Practical Statistics for Medical Research. London, UK: Chapman Hall; 1997. | |
Steyerberg EW. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. Berlin, Germany: Springer Science+Business Media. doi: 10.1007/978-0-387-77244-8. Available from: http://www.springer.com/us. | |
Damiano R, Autorino R, De Sio M, Giacobbe A, Palumbo IM, D’Armiento M. Effect of tamsulosin in preventing ureteral stent- related morbidity: a prospective study. J Endourol. 2008;22:651–655. | |
Nawaratne S, Brien JE, Seeman E, et al. Relationships among liver and kidney volumes, lean body mass and drug clearance. Br J Clin Pharmacol. 1998;46:447–452. | |
Paick SH, Park HK, Byun SS, Oh SK, Kim HH. Direct ureteric length measurement from intravenous pyelography: does height represent ureteric length? Urol Res. 2005;33:199–202. |
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.