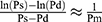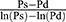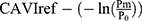The Background of Calculating CAVI: Lesson from the Discrepancy Between CAVI and CAVI₀

Introduction

Arterial stiffness reflects the degree of arteriosclerosis; it is considered to be a good predictor of cardiovascular events.¹ It also is an index of vascular function in conjunction with cardiac function. Arterial stiffness is physically represented by an elastic modulus, but it is not easy to measure in blood vessels in vivo.² Meanwhile, it has been shown that the elastic modulus of blood vessels is related to pulse wave velocity (PWV),^3,4 and PWV has become widely used around the world as a surrogate marker of arterial stiffness since it is relatively easy to measure.¹

However, the drawback of PWV is its essential dependence on blood pressure at the measuring time.^5,6 Since the measured value of PWV changes, it is difficult to determine whether it is due to changes in blood pressure or due to changes in the proper arterial stiffness. To overcome this disadvantage, attempts were made to devise a new index. Hayashi et al⁷ proposed the stiffness parameter β, which provides the proper arterial stiffness and it is not affected by the blood pressure at measuring time. Subsequently, Kawasaki et al⁸ reported a method of calculating β using an ultrasonic diagnostic apparatus, which has become widely used clinically. However, this stiffness parameter β was applied to only one part of the artery.

In 2004, the cardio–ankle vascular index (CAVI) was developed⁹ based upon the Kawasaki’s β formula and the Bramwell-Hill equation. CAVI reflects the arterial stiffness of the arterial tree from the origin of the aorta to the ankle arteries. In this system, PWV is used. The independency of CAVI has been theoretically and experimentally verified. Throughout the world many researchers have applied this index in numerous studies; nearly 600 relevant papers have been published over the last 15 years, and the concept of CAVI has become widely accepted with many valuable findings documented.^10–12

Recently, however, Spronck et al^13–15 proposed a variant index termed CAVI₀ asserting that CAVI is dependent on blood pressure, whereas CAVI₀ is not. Thus, a controversy was raised regarding the independency of CAVI and CAVI₀ from blood pressure at the measuring time.^16,17 Since that time, several papers reporting the comparison between CAVI and CAVI₀ have been published, but the difference between the two indices is difficult to understand in most studies because they compared the indices using mathematical formulas and statistical analyses.

The purpose of this review is to describe the lesson learned from this controversy. We clarify the features of PWV used in the calculation of CAVI and verify CAVI with reference to CAVI₀ based on the features of PWV. Further, we describe the validity of CAVI by showing actual clinical data provided in recent literature. In addition, the recent reports on the advantages and claimed disadvantages of CAVI are reviewed.

Blood Pressure Dependency in PWV

Arterial stiffness can be presented by bulk modulus, which means how hard is it for the vessel to expand in diameter (D) against the change of pressure (P), and the relationship of PWV with bulk modulus is shown by the Bramwell-Hill equation (Supplement Seq.1). If the bulk modulus is constant, PWV is also constant and not dependent on P. However, in the actual artery, the bulk modulus or PWV changes in accordance with P, which makes it difficult to measure the inherent arterial stiffness.

In order to overcome this problem, Hayashi et al⁷ found that P and D have an exponential relationship; they defined the β formula, which provides the index of inherent arterial stiffness independent of P (Supplement Seq.2).

Combining the β formula and the Bramwell-Hill equation yields Equation 1. (Supplement Seq.3-8)

(1)

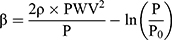
[β: specific stiffness of the blood vessel, ρ: blood density, PWV: pulse wave velocity, P: blood pressure, P₀: reference blood pressure]

This equation shows the relationship between PWV, P and β. It may look complex, but the essence is quite simple, since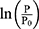 is generally small, as will be shown later, and it can be regarded as negligible. Then, Equation 1 can be transformed into Equation 2

(2)

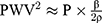
As ρ can be considered as constant, Equation 2 means that PWV² is approximately proportional to blood pressure P for the same β. This is the essential nature of the blood pressure dependency of PWV in the artery where diameter change has an exponential relationship with P. Figure 1 shows the relationship between P and PWV calculated by Equation 1. Obviously, PWV is almost proportional to the square root of blood pressure P for the same β.

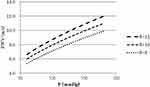Figure 1 Relationship between P and PWV in Equation 1. Abbreviations: P, blood pressure; PWV, pulse wave velocity; β, specific stiffness of the blood vessel.

In other words, since PWV² is almost proportional to P, proper arterial stiffness which is independent of blood pressure can be obtained by dividing PWV² by P as a proportional coefficient.

PWV Change in Cardiac Cycle

As stated above, PWV² is approximately proportional to P for the same β, and as such, PWV changes in accordance with the blood pressure between diastolic pressure (Pd) and systolic pressure (Ps) during the cardiac cycle. It is already known that PWV at systolic pressure (PWVs) is larger than that at diastolic pressure (PWVd) as shown in Figure 2. In the past, PWV could only be measured on a foot-to-foot basis in the pulse wave, which corresponds to the diastolic phase. Recently, with the progress of measuring technologies, such as high speed and high-resolution ultrasound imaging or MRI, it has become possible to measure PWV at various points in the cardiac cycle. Many papers have already reported that PWV in the systolic phase has a greater clinical significance than in the diastolic phase. Mirault et al¹⁸ revealed changes in PWV during the cardiac cycle using an ultrafast ultrasound imaging system in healthy volunteers (n=102) and in vascular Ehlers-Danlos syndrome (vEDS) patients (n=37). vEDS is a rare vascular disease resulting in mutations in the collagen type III gene. PWV at early-systole (PWVearly) and end-systole (PWVend) were 5.6±1.2m/s and 7.3±2.0m/s, respectively, in healthy subjects, and 6.0±1.5m/s and 6.7±1.5m/s, respectively, in vEDS patients.¹⁸ The results clearly indicate that PWV at the systolic phase is much larger than that at the diastolic phase. The lower increase of PWV in vEDS patients was attributed to the lack of stiffening due to the abnormal collagen in the arterial wall.

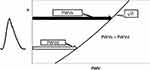Figure 2 Schematics of the PWV in the cardiac cycle. Abbreviations: P, blood pressure; PWV, pulse wave velocity; PWVs, PWV at systolic blood pressure; PWVd, PWV at diastolic blood pressure.

Hermeling et al¹⁹ also reported the differences of PWV in the cardiac cycle and suggested a greater clinical significance of PWV at the systolic phase.

Corresponding Blood Pressure of PWV Used in CAVI Calculation

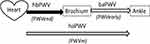
As shown in Figure 3, VaSera system measures haPWV, which is the PWV from the heart to the ankle to obtain CAVI. In fact, haPWV was obtained by dividing the length of the arterial tree by the time of the pulse from the heart to the ankle. The trouble is the difficulty to identify the accurate time for the pulse to start at the origin of the aorta. Thus, the VaSera system uses a slightly complex contrivance. The pulse propagation time from heart to ankle is divided into two time periods, one is the time from heart to brachium (hbTime), and the other is the time difference between the brachium and ankle (baTime). The hbTime is measured as the time from heart sound II to the dicrotic notch of the pulse at the brachium. Since hbTime is measured at the blood pressure level of the dicrotic notch, the heart to brachium PWV (hbPWV) corresponds to the PWVend in the cardiac cycle. On the other hand, since baTime is measured at the foot level of the pulse waves, the brachial-ankle PWV (baPWV) corresponds to PWVearly. As a result, haPWV is the PWVm, which is the PWV at the mid pressure (Pm) between Pd and Ps. Although the blood pressure level at end-systole phase depends on the case and Pm may fluctuate, it is not a big error to evaluate it as Pm = (Ps + Pd)/2. The important fact here is that the corresponding blood pressure of haPWV in CAVI is not Pd, but rather Pm.

Figure 3 Schematics of the PWV from heart to ankle measured by cardio-ankle vascular index. Abbreviations: PWV, pulse wave velocity; hbPWV, heart to brachium PWV; baPWV, brachium to ankle PWV; haPWV, heart to ankle PWV; PWVend, PWV at end-systole phase; PWVearly, PWV at early-systole phase.

Conceptual Meaning of the CAVI

Now, we look over the formula again simply to clarify the meaning of CAVI.

CAVI equation is shown as Equation 3.

(3)

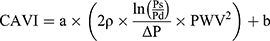
[PWV: pulse wave velocity of the arterial tree from the origin of the aorta to the ankle, Ps: systolic blood pressure, Pd: diastolic blood pressure, ρ: blood density, 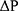: Ps–Pd, a, b: coefficients²⁰].

The essence of CAVI is inside the parentheses of Equation 3, and we define it as CAVI’ in Equation 4, which is the value without coefficients²⁰ “a” and “b”

(4)

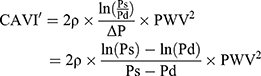
In Equation 4, 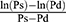, a blood pressure term is mathematically proven¹⁷ to be approximated by .

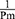In this article, we refrain from mathematical expressions as much as possible and show them schematically. The blood pressure term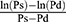 is the average rate of change in natural logarithm blood pressure ln(P) when the blood pressure P changes from Pd to Ps. This term is shown as an incline of the line which cuts the curve of ln(P) at Pd and Ps (Figure 4); obviously, this incline closely resembles that in a tangent of ln(P) at Pm. Basically, the incline of the tangent is the differential value of the curve. Due to the interesting nature of logarithm’s differentiation, the differential value of ln(P) is 1/P, and the incline of the tangent at Pm is 1/Pm. Thus, Equation 5, which represents the important attribute of CAVI, is introduced.

(5)

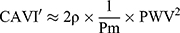
Figure 4 Schematics to show . Abbreviations: P, blood pressure; Ps, systolic blood pressure; Pd, diastolic blood pressure; Pm, mid-pressure.

As stated in the clause of blood pressure dependency of PWV, PWV² is approximately proportional to blood pressure P. In CAVI, also as stated, PWV corresponds to Pm, and by dividing PWV² with Pm, an inherent arterial stiffness which is independent of blood pressure can be obtained. We have reported in a large population study that haPWV in CAVI is mostly correlated with Pm.¹⁷ This is the essential meaning of CAVI.

Verification with Clinical Data

Now, we verify the validity of CAVI with the actual clinical data. We presented the comparison results between CAVI and CAVI₀ based on the medical examination data of a large population.²¹ By reviewing the data of the paper, we verified each element of CAVI. The studied populations are in two groups: a healthy group (n=5,293; 3,071 women and 2,222 men) and a hypertensive group (n=3,338; 1,006 women and 2,332 men).

Re-Conformation of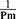

The relationship between Pm and 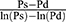, the reciprocal of the blood pressure term of CAVI, was previously presented in a publication.¹⁷ Here, we show the separate results for the healthy group and the hypertensive group. As shown in Figure 5A and B, the coefficients of correlation were r=0.997 (p<0.001) for both groups, indicating that the blood pressure term of CAVI is almost equal to .

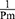Figure 5 Relationship between and Pm for healthy group (A) and hypertensive group (B) analyzed with the data from Shirai et al.21 Relationship between CAVIref and for healthy group (C) and hypertensive group (D) analyzed with the data from Shirai et al.21 Abbreviations: Ps, systolic blood pressure; Pd, diastolic blood pressure; Pm, mid-pressure; CAVIref, cardio-ankle vascular index (CAVI) with reference blood pressure; P0, reference blood pressure.

Influence of Reference Blood Pressure Term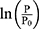

The basic equation Equation 1 has a reference blood pressure term of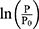 , but CAVI does not have this term. Therefore, in order to assess the effect of the presence or absence of the term, an equation including a reference blood pressure term in which P=Pm is substituted into Equation 1 is defined as CAVI_ref in Equation 6.

(6)

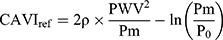
When the values with and without 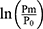are compared in Equation 6, the influence of the reference blood pressure term is evaluated, as shown in Figure 5C and D. The coefficients of correlation were r=0.997 and r=0.998 (p<0.001for both) for the healthy group and hypertensive group, respectively, indicating that the influence of the reference blood pressure term is small and negligible.²¹

Comprehensive Comparison of the Values

Now, we compare the data comprehensively. Here, CAVI₀ formula¹³ is described in Equation 7.

(7)

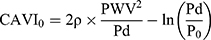
This equation is obtained by substituting P = Pd in Equation 1, and the reason for the substitution is based on the assumption that PWV in CAVI is the PWV at Pd, which causes markedly irrational results.

First, the relationship between Pm and CAVI_ref is compared with the relationship between Pd and CAVI₀. The purpose of this comparison is to confirm which blood pressure, Pm or Pd, is appropriate to divide the same PWV² to obtain the blood pressure-independent inherent arterial stiffness. The results are shown with mean values and standard deviation data plotted in every 2 mmHg group (Figure 6). In both healthy and hypertensive groups, CAVI_ref has a slightly positive relationship with Pm, and it is acceptable because it is considered to have an increase in arterial stiffness due to long-term exposure to blood pressure. On the contrary, CAVI₀ has a negative relationship with Pd, and this is obviously strange.

Figure 6 Relationship of the mean values of CAVIref and CAVI0 with Pm and Pd in every 2 mmHg groups for healthy and hypertensive groups analyzed with the data from Shirai et al.21 Abbreviations: CAVIref, cardio-ankle vascular index (CAVI) with reference blood pressure; CAVI0, a variant index of cardio-ankle vascular index; Pm, mid-pressure; Pd, diastolic blood pressure.

Furthermore, it was reported²¹ that CAVI₀ values in hypertensive women aged 30–39 years are significantly less than the values of healthy women. The reason for these questionable results is the mismatching of the calculation in that PWV² is divided by Pd instead of Pm.

Next, CAVI₀ and CAVI’, without coefficients of “a” and “b”, are compared with CAVI_ref, thought to be the theoretical value of inherent arterial stiffness, as shown in Figure 7. CAVI’ is approximately equal to CAVI_ref, but CAVI₀ shows clearly over-estimated values in both healthy and hypertensive groups. This is the essence of the discrepancy between CAVI and CAVI₀ found in recent publications.

Figure 7 Relationship of CAVI’ and CAVI0 with CAVIref for healthy and hypertensive groups analyzed with the data from Shirai et al.21 Abbreviations: CAVI’, cardio-ankle vascular index (CAVI) without the coefficients “a” and “b”; CAVI0, a variant index of cardio-ankle vascular index; CAVIref, CAVI with reference blood pressure.

Recent Pro and Con Articles on CAVI

First, we review an article critical of CAVI. Ato²² published a paper stating that CAVI is problematic. This allegation is based on misunderstandings about CAVI, and therefore, we were obliged to resolve those misunderstandings here.

The paper of Ato²² argues that the coefficients “a” and “b” of CAVI, defined in the previous study,²⁰ are inappropriate because they underestimate values in the high range. However, this point has been already discussed in our previous paper,²⁰ and it has been proven that the presence or absence of the coefficient does not change the clinical significance. The coefficients were set for the purpose of matching with the Hasegawa PWV scale, which already had vast clinical data, at the time of the development of CAVI, and clinical effectivity has been widely been demonstrated. However, since the coefficient values were disclosed in our previous paper,²⁰ it has also recently become possible to study with values that do not include coefficients. The data can simply be converted by a tool (Supplementary digital content 1). In the conversion tool, the CAVI values without the coefficients “a” and “b” are expressed as “CAVIβ”, which is described as CAVI’ in this article.

The next point is the assertion that CAVI depends on blood pressure, citing papers²³ in which CAVI is changed in autonomic nerve stimulation tests such as the Cold pressor test (CPT) and Hand grip test (HGT). However, the fact is that with stimulated sympathetic nerves by CPT or HGT, the stiffness of blood vessels including smooth muscles increases, along with the change of blood pressure. This mechanism has been explained by numerous articles.^24–26 CAVI correctly showed the increase of stiffness, and this result does not mean that CAVI is blood pressure dependent at the measuring time.

Since this point is often confused, the meaning of blood pressure independency is clarified here. Arterial stiffness is basically divided into the inherent stiffness and blood pressure-dependent change, as shown in Figure 8. The inherent stiffness includes physiological and functional elements as well as organic and structural elements. The former elements can change acutely, while the latter changes over the long term. Among them, CAVI only eliminates the blood pressure-dependent change, and it represents the inherent arterial stiffness including both organic and structural, and physiological and functional elements. Therefore, changes in physiological and functional stiffness, which are caused by CPT or such autonomic nerve stimulation, are reflected correctly. This is the true value and the meaning of blood pressure independency.

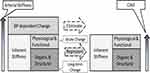Figure 8 Schematics of the meaning in blood pressure independency of the arterial stiffness. Abbreviation: CAVI, cardio-ankle vascular index.

With some more unreasonable claims, not even worthy of discussion, the paper²² as a whole is questionable based on misunderstandings.

Next, we introduce one of the most recent publications showing the usefulness of CAVI. Kirigaya et al²⁷ published an excellent article investigating the impact of arterial stiffness assessed with CAVI on the long-term outcome after acute coronary syndrome (ACS). A total of 387 consecutive patients with ACS were enrolled and CAVI and baPWV were measured. The patients were divided into two groups of low-CAVI (<8.35) and high-CAVI.

As a result, Kaplan-Meier analysis demonstrated a significantly higher probability of adverse cardiovascular events (MACE) in the high-CAVI group, and multivariate analysis suggested that CAVI was an independent predictor of MACE, but baPWV was not.

Also, the incremental predictive value of adding CAVI to GRACE score (GRS) was investigated, and stratified by CAVI and GRS, a significantly higher rate of MACE was found in patients with both higher CAVI and higher GRS than the other groups. Further, the addition of CAVI to GRS enhanced net reclassification improvement and integrated discrimination improvement.

The impact of this paper of Kirigaya et al²⁷ is that it has shown that arterial stiffness, determined using CAVI, was an independent long-term predictor of MACE in patients with ACS, and that CAVI can improve the risk stratification based on GRS. Blood pressure is important for prognosis prediction, and it is thought that baPWV, which contains a marked blood pressure factor, has higher prognostic prediction ability, but in reality, it is not significant in baPWV, and CAVI is significant. This result has doubtlessly great significance in the future research on arterial stiffness.

Limitations and Perspective

Both in CAVI and CAVI₀, peripheral vessels are included in the measurements. When the subjects have peripheral arterial diseases such as atherosclerosis obliterans, the measurements will be unreliable. Also, it has been claimed that evaluating a longer arterial length should add important additional information to the measurements, but it could be interpreted also as confounding factors.²⁸ These are the limitations in the measurements of both CAVI and CAVI₀.

However, in this association, it was reported that the response of arteries to the vasodilating agents such as nitroglycerin is different between central and peripheral,²⁹ suggesting that the meaning and role of arterial stiffness differ depending on the segments. As a perspective, more useful information would be obtained in the future if blood pressure-independent arterial stiffness for both central and peripheral segments could be measured separately and more easily.

Conclusion

The conceptual meaning of CAVI is reconfirmed and verified to be as follows: Arterial stiffness is represented by the bulk modulus of the blood vessel, which is approximately proportional to blood pressure P. When it is divided by P, a proportionality constant is obtained, representing arterial stiffness independent of blood pressure.

CAVI and CAVI₀ are compared with recent findings, and the claim that CAVI₀ is less blood pressure dependent than CAVI has been shown to be suspicious, although the proposition of CAVI₀ has contributed to deeper discussions on the blood pressure independency of CAVI. As a summary, common and different points between CAVI and CAVI₀ are shown in Table 1.

Table 1 Common and Different Points Between CAVI and CAVI0

We conclude that CAVI₀ is questionable because of the mismatching in the formula and CAVI is a reliable and sensitive index of blood pressure-independent arterial stiffness, in both organic and functional components.