Back to Journals » Patient Preference and Adherence » Volume 12
Research of an emergency medical system for mass casualty incidents in Shanghai, China: a system dynamics model
Authors Yu W, Lv Y, Hu C, Liu X, Chen H, Xue C, Zhang L
Received 30 October 2017
Accepted for publication 2 December 2017
Published 31 January 2018 Volume 2018:12 Pages 207—222
DOI https://doi.org/10.2147/PPA.S155603
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Naifeng Liu
Wenya Yu,* Yipeng Lv,* Chaoqun Hu,* Xu Liu, Haiping Chen, Chen Xue, Lulu Zhang
Department of Military Health Service Management, College of Military Health Service Management, Second Military Medical University, Shanghai, People’s Republic of China
*These authors contributed equally to this work
Objectives: Emergency medical system for mass casualty incidents (EMS-MCIs) is a global issue. However, China lacks such studies extremely, which cannot meet the requirement of rapid decision-support system. This study aims to realize modeling EMS-MCIs in Shanghai, to improve mass casualty incident (MCI) rescue efficiency in China, and to provide a possible method of making rapid rescue decisions during MCIs.
Methods: This study established a system dynamics (SD) model of EMS-MCIs using the Vensim DSS program. Intervention scenarios were designed as adjusting scales of MCIs, allocation of ambulances, allocation of emergency medical staff, and efficiency of organization and command.
Results: Mortality increased with the increasing scale of MCIs, medical rescue capability of hospitals was relatively good, but the efficiency of organization and command was poor, and the prehospital time was too long. Mortality declined significantly when increasing ambulances and improving the efficiency of organization and command; triage and on-site first-aid time were shortened if increasing the availability of emergency medical staff. The effect was the most evident when 2,000 people were involved in MCIs; however, the influence was very small under the scale of 5,000 people.
Conclusion: The keys to decrease the mortality of MCIs were shortening the prehospital time and improving the efficiency of organization and command. For small-scale MCIs, improving the utilization rate of health resources was important in decreasing the mortality. For large-scale MCIs, increasing the number of ambulances and emergency medical professionals was the core to decrease prehospital time and mortality. For super-large-scale MCIs, increasing health resources was the premise.
Keywords: system dynamics model, emergency medical system, mass casualty incidents
Introduction
Mass casualty incidents (MCIs) are increasing. This is especially true of MCIs caused by non-natural factors, such as terrorist attacks,1,2 explosions,3,4 and burns.5 In fact, the number of MCIs has shown an increasing trend in the past 8 years6 and an epidemiological study has pointed out that the number of MCIs has gone beyond expectations.7 Without exception, MCIs in China have continued to increase. Such incidents include the accident of metro line 10 in Shanghai, which injured 271 people in 2011,8 the Bund stampede also in Shanghai, which killed 36 people and injured 49 people in 2014,9 a factory explosion in Kunshan city, which caused 97 deaths and injured 163 people in 2014,10 a warehouse explosion in Tianjin city, which killed 165 people and injured 798 people in 2015,11 the amusement park explosion in Taiwan, which killed 12 people and injured 498 people in 2015,4 and a car accident in Jiangsu province, which killed three people dead and wounded 31 people.12
The large amount of wounded and dead caused by MCIs gives impetus to globally study the emergency medical system for MCIs (EMS-MCIs), such as the emergency management system (EMS) in the USA, which have promoted the efficiency of MCI rescue.13 In addition, global research on MCIs covers various areas, such as prehospital and hospital rescues, triage, medical evacuation, and emergency support systems. Of these, studies on hospital emergency rescue have attracted the most attention, including emergency rescue capability,2 preparedness,14 organization,15 crowd control,16 and hospital response programs.17,18 Research on prehospital emergency rescue has included triage and medical evacuation, such as DIORAMA-II system proposed by the USA,19 a new triage method established by Spain,20 and a doctor-helicopter system in Japan.21–23 To conclude, a handful of developed countries have achieved some success in promoting rescue efficiency and decreasing the mortality of MCIs.
The Chinese government has fully realized the importance of preventing MCIs and improving rescue efficiency since the beginning of the 21st century. The State Council has proposed to establish and revise the emergency plan for MCIs to minimize losses.24,25 Scholars in China have focused mainly on triage, including triage method,26 efficiency,5 and training of triage.27 Hospital rescue measurements also caused attention, including clinical treatment methods28 and auxiliary examination.29,30 However, only a small number of researchers have focused on emergency strategies.31 In summary, studies in China have focused on specific aspects of rescue in MCIs but have lacked studies covering the entire rescue process to improve the overall efficiency from prehospital to hospital.
Currently, studies have concentrated on retrospective research and emergency rescue methods. However, considering the sporadic, nonreplicable, and high-risk nature of MCIs, modeling research on MCIs shows an obvious methodological advantage. This method enables the simulation of the occurrence and rescue for a great number of MCIs, based on the limited data from retrospective studies, which provides the possibility of exploring MCI rescues in greater depth. Therefore, simulation studies of EMS-MCIs, based on modeling, have garnered a great deal of attention.13 For example, Hupert et al32 established a simulation model of MCI care and suggested that rapid response determined the effectiveness of MCI rescue projects.
However, in China, there is an extreme absence of research on modeling EMS-MCIs, especially rapid decision-support systems based on computer technology. Shanghai, as one of the largest metropolis and economic centers of China, houses >24 million residents and faces great challenges in the emergency medical system.33 Therefore, this study aimed to establish a system dynamics (SD) model of EMS-MCIs in Shanghai, which reached the goals of modeling research to improve MCI rescue efficiency in China for the first time, and to provide a possible method of making rapid rescue decisions during MCIs.
Methods
Model description
Problem
First, the EMS-MCIs in Shanghai lacked a rapid response program and the response speed of the organization and command department needed to be strengthened. Second, each ambulance in Shanghai served ~40,000 people,34 which could only meet daily demands and could not accommodate MCI rescues appropriately, leading to elongated prehospital times and high mortality.
Agents and association of the model
The model consisted of four agents that specifically included casualties, hospitals, the government, and the emergency center. As would be the case in reality, the four agents interacted with each other within the model. The severity of the injured determined the overall medical demand, the emergency rescue capability of hospitals decided the hospital rescue efficiency, the information and response of the government influenced the organization and command efficiency, and the emergency center was responsible for the prehospital emergency rescue efficiency and emergency health resource allocation.
Causal loop diagram
A search of the literature revealed that prehospital and hospital rescues, scale of MCIs, injury severity, medical rescue time, and emergency decision making were key factors of mortality.13 Therefore, based on the basic situation of China and the investigation on MCIs in Shanghai, factors included in this study were the scale of MCIs, prehospital time, hospital rescue capability, and efficiency of organization and command. Figure 1 reflects the interaction of these factors. The specific meaning of casual loop diagram was as follows.
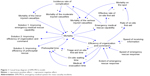  | Figure 1 Casual loop diagram of EMS-MCIs model. |
The scale of MCIs and injury characteristics
Mortality of individuals involved in MCIs was directly influenced by the severity of injury. Mortalities of minor injuries, moderate injuries, and serious injuries varied, and the proportion of the three types of casualties determined the medical demand. Moreover, some critically injured casualties shared the risk of death on the spot, which was primarily affected by on-site first-aid measures.
Organization and command of MCIs’ rescue
The efficiency of organization and command was influenced by the speed that the emergency department received MCIs’ information and the speed and the extent of emergency response. In addition, the efficiency would indirectly affect mortality by prehospital and hospital rescues. Mortality would be lower with an increase in efficiency.
Prehospital emergency rescue of MCIs
The key to significantly reduce mortality was the decreasing prehospital time, which included the on-site waiting time, triage and on-site first-aid time, and medical evacuation time. Mortality would increase with an increase in prehospital time.
Hospital rescue of MCIs
Hospital rescue capability referred to hospital treatment capacity, which reflected a hospital’s clinical ability and its treatment effect. Hospital rescue capability decided the success rate of treatment and the incidence rate of complication. Higher incidence rates of complication would increase the mortality of individuals involved in MCIs.
Stock-flow diagram
Hypothesis of model
To simplify the analysis, the model assumed that the main factor influencing hospital mortality was complication; the process of organization and command was summarized as judgment, planning, decision making, and organization; and all casualties were transferred into hospitals through the emergency center. Moreover, hospitals were all tertiary (A class) hospitals because Shanghai possesses 32 tertiary (A class) hospitals, all of which have >500 beds; these health resources were enough to meet the medical demand of MCIs caused by non-natural factors. Additionally, because the operation time was set as 72 hours, the model assumed there was no change in the fixed assets and market profits of hospitals.
Parameters of model
This model included six types and a total of 102 variables, which interacted with each other and constituted the SD model of EMS-MCIs in Shanghai (Figure 2). The stock variable of the model was the state variable, represented by a rectangle (eg, demand judgment). The input and output of the stock variable were connected by a flow variable (eg, rate of receiving information), which was a rate variable and connected to the stock variable with the double arrows. The relationships among variables were lined with single arrows, including auxiliary (eg, emergency medical demand), initial (eg, initial number of available ambulances), constant (eg, proportion of minor injuries), and observational (eg, mortality) variables.
Subsystems of model
The model consisted of five subsystems, namely, a subsystem of the occurrence of MCIs, a subsystem of hospital emergency medical rescue, a subsystem of organization and command, a subsystem of the emergency center, and a subsystem of casualty outcome. These five subsystems were associated and interacted via input and output variables.
Figure 3 represents the subsystem of the occurrence of MCIs. The number of casualties was determined by the population involved in the MCI and the rate of injury. Casualties were classified into minor, moderate, and serious injuries. Among the minor injured, some of casualties without medical demand initially would increase in demand as time progressed. All the moderate injured casualties required medical attention. Only some critically injured casualties among the serious injured had the risk of death on the spot, and the rest had medical demand. The on-site mortality was influenced by on-site first-aid time. In addition, casualties were transferred into hospitals through emergency departments; thus, the actual medical demand was the emergency medical demand, and the hospitalized medical demand was decided by the rate of hospitalization.
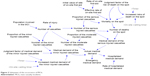  | Figure 3 Subsystem of the occurrence of MCIs. |
A representation of the subsystem of hospital emergency medical rescue is presented in Figure 4. The assessment of hospital emergency medical rescue capability was based on the ratios of medical supply and demand. Capability was considered to increase with the extent that the medical demand was met by the supply. The medical rescue capability was influenced by fixed assets and the number of medical staff, which can be constructed according to the Cobb–Douglas production function.
  | Figure 4 Subsystem of hospital emergency medical rescue. |
A representation of the subsystem of organization and command is presented in Figure 5. Organization and command was the process of demand judgment, medical evacuation planning, medical evacuation decision, and organization, which was ultimately reflected as the implementation rate of organization and command. The judgment and planning were influenced by the information system (receiving and processing). The decision and organization were affected by the implementation of the plan and decision, respectively. During this process, a delay effect due to information transmission was existed.
The subsystem of the emergency center is presented in Figure 6. Prehospital time was the sum of on-site waiting time, triage and on-site first-aid time, and medical evacuation time. The length of prehospital time determined the rank of timeliness. On-site waiting time was mainly affected by the organization and command efficiency. Triage and on-site first-aid time were determined by the number of medical staff and medical demand. Medical evacuation time was decided by the number of ambulances.
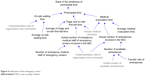  | Figure 6 Subsystem of the emergency center. |
The subsystem of casualty outcomes is presented in Figure 7. Mortality was determined by on-site deaths, as well as minor, moderate, and serious injuries. Minor, moderate, and serious injuries were influenced by complication, timeliness of medical rescue, and medical rescue capability.
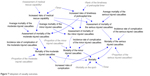  | Figure 7 Subsystem of casualty outcomes. |
Variables and equations
First, the initial values of variables and constant variables were extracted from a survey on MCIs in Shanghai, the China Health Statistics Yearbook 2015, the Shanghai Statistical Yearbook 2016, Shanghai Municipal Health Commission statistics, literatures, and expert consultations.
Second, the stock variables were based on initial variables. The value of a stock variable was the sum of its initial value and the input variable. For example, the equation of demand judgment was “0.4+ IF THEN ELSE (difference of demand judgment > rate of receiving information, rate of receiving information, difference of demand judgment)”. Equations of medical evacuation plan, medical evacuation decision, and organization and command situation were similar.
Third, the current study constructed equations of auxiliary variables based on initial variables, constant variables, and change rate. The structure of such equations was “initial values/constant values × EXP (time × change rate)”, which reflected the increasing trend with time. For example, the increased medical demand of the minor injured casualties = judgment factor of medical demand of the minor injured casualties × EXP (IF THEN ELSE [time ≤ on-site waiting time, time, on-site waiting time] ×0.013).
Fourth, some uncertain factors and complex mechanisms were determined through brainstorming and the Delphi method (including 15 experts). The power function equations were constructed according to the Cobb–Douglas function. For example, emergency medical rescue capability = factor of emergency medical rescue capability × number of emergency medical stafffactor of emergency manpower × fixed assets(1 − factor of emergency manpower)/10,000.
Fifth, logic equations were determined according to “IF THEN ELSE” function. The structure was “IF THEN ELSE (judgment condition, the value when satisfying the judgment condition, and the value when the judgment condition cannot be satisfied)”. For example, the rank of emergency medical rescue capability = IF THEN ELSE (ratio of emergency medical supply and demand ≥1, 1, 2).
Sixth, delay equations were determined. Some quantitative changes would be triggered after a delay; for example, the implementation of organization and command could be conducted after the information was transmitted. For example, the implementation rate of organization and command = SMOOTH (organization and command situation, time +0.01).
All variables included in the model are shown in Appendix A.
Model validation
To verify the validity of the model, the model validation experiment was conducted based on the data of the Bund stampede in Shanghai on December 31, 2014. The population involved in this MCI was set as 1,040, according to the population density of the event area. The observational variables were mortality, average prehospital time, and the proportions of minor, moderate, and serious injuries. Verification results are shown in Table 1. It can be seen that the deviation between the actual data and simulated data was in the range of −7.14% to 3.03%, which can be deemed as a reasonable range. Therefore, this model was considered reliable and reasonable.
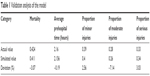  | Table 1 Validation analysis of the model |
Sensitivity analysis
Sensitivity analysis was utilized to compare whether the model would fluctuate dramatically after changing some parameters and structures, which can be employed to evaluate the reliability and rationality of a model.35 The sensitivity of parameters was calculated by DY(t)/Y(t) and DX(t)/X(t), which represented the change of the output variable and the sensitive variables, respectively. Therefore, the formulation of sensitivity analysis was 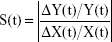 .
.
In this study, the output variable was mortality. The four sensitive parameters were transfer rate of ambulances, efficiency of information system, increased risk of death caused by complication, and initial value of effective rate of first-aid, with a change rate of −10% to 10%. The model was operated 200 times, and the sensitivity analysis was conducted by Vensim (Figure 8). Among the 200 situations, 50%, 75%, 95%, and 100% were in the yellow, green, blue, and grey areas, respectively. The result suggested that mortality remained the overall tendency and fluctuated slightly in a reasonable range. Thereby, this model can be considered stable, reliable, and suitable for simulation analysis.
  | Figure 8 Sensitivity analysis of EMS-MCIs model. |
Intervention scenarios
This study designed four intervention experiments to simulate different scales of MCIs and explore the effects of interventions under various scales of MCIs. The control group was always the current situation, which was the baseline where no interventions were applied. After changing some parameters, the observational groups were compared with the control group. The simulation time of the model was set as 72 hours, and the parameters in the intervention experiments are listed in Table 2.
  | Table 2 Changes to the parameters of different intervention scenarios |
Results
Intervention experiment 1: simulation of the different scales of MCIs
In this experiment, only the population involved in MCIs was changed. The results showed that mortality was higher with the increase of the scale of MCIs. When 200 people were involved in MCIs, the medical rescue capability was in the best condition and remained good conditions under the sizes of 1,000 or 2,000 people. In addition, the organization and command efficiency showed an obvious increasing trend after 4 hours of MCIs, but reaching the lowest point after 8 hours. Moreover, the timeliness of prehospital time was always very poor, the triage and on-site first-aid time grew significantly when the scale reached to 2,000 people, and medical evacuation time rose with the increasing scale (Figure 9).
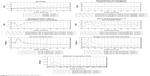  | Figure 9 Results of intervention experiment 1. |
According to above results, the medical rescue capability was good in most conditions. Considering that the possibility of MCIs involving >5,000 people is small, this study did not conduct experiments on medical rescue capability and all parameters were set based on the current situation. In addition, as different scales of MCI would generate various medical demands, the following experiments (intervention experiment 2–4) compared the results of the same intervention performed in the four scales of MCI to determine the different effects of interventions under different size MCIs.
Intervention experiment 2: simulation of different allocations of ambulances
In this experiment, only the number of available ambulances and the transfer rate were changed. The results suggested that mortality declined significantly when 2,000 people involved in an MCI and mortality decreased sharply within 24 hours when 1,000 people were involved. However, the effect was not obvious when the population involved in the MCI was <200 or >5,000. Similarly, this intervention experiment would improve the timeliness of prehospital time if the scale was <5,000 people, with most significant effect under the size of 2,000 people (Figure 10).
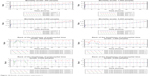  | Figure 10 Results of intervention experiment 2. |
Intervention experiment 3: simulation of different allocations of emergency medical staff
In this experiment, only the number of emergency medical staff of emergency centers was adjusted. The results indicated that the intervention scenarios had no effect on mortality; triage and on-site first-aid time were shortened with the growth of emergency medical staff. This effect was more evident during 4–16 hours under the scale of 2,000 people. However, a sustained effect was observed under the scale of 5,000 people (Figure 11).
  | Figure 11 Results of intervention experiment 3. |
Intervention experiment 4: simulation of efficiency of organization and command
In this experiment, only values of the efficiency of the information system, average judgment, planning, decision, and organization condition were changed. The results showed that the effect on mortality was significant under the scale of 5,000 people, especially within 12 hours for the scale of 2,000 people. In addition, mortality was decreased dramatically when the efficiency was improved to an ideal level under the size of 200 people. Furthermore, timeliness of prehospital time could be improved through an increase in efficiency. The most significant effect was observed during 4–16, 4–24, and after 12 hours under the 200, 1,000, and 2,000 individual scales, respectively (Figure 12).
  | Figure 12 Results of intervention experiment 4. |
Discussion
Based on intervention experiments, the efficiency of EMS-MCIs can be improved by shortening prehospital time and improving organization and command efficiency. However, to maximize effectiveness, scenarios should be adjusted according to the scales of the MCI.
Mortality would likely increase with the growing scale of an MCI. The current EMS-MCIs could only meet the demand of small size MCIs, as efficiency was not ideal for the rescue of larger scales of MCIs, especially for MCIs involving >5,000 people. Specifically, the efficiency observed of organization and command was not good, especially within 4 hours (the best time to rescue on-site casualties). This may be attributed to the slow response speed of the organization and command department. After 5 hours, medical rescue was mainly at the stage of hospital rescue. However, the organization and command efficiency decreased dramatically during this time, which led to chaos in hospitals and a failing to meet medical demands. Additionally, the timeliness of prehospital time was poor, especially for the scale of >1,000 people. Analyses of prehospital time suggested that the triage and on-site first-aid time showed a significant delay if the scale was >2,000 people, which was mainly attributed to a shortage of emergency medical staff, leading to long queues and retention on the scene. Moreover, the medical evacuation time presented an evident increasing tendency because of the limited number of ambulances, which was especially significant with the increasing size of MCIs. Incidentally, because the current ambulances in Shanghai were owned and managed by Shanghai Medical Emergency Center, all ambulances could only provide basic life support. It means that patients could not receive advanced life support and they have to be sent to hospitals as soon as possible. Therefore, it is of great importance to improve the efficiency of organization and command during the prehospital stage and the initial stage of hospital rescue. Increasing the number of ambulances and emergency medical staff was the key to shorten prehospital time and decrease mortality caused by delay under larger scale MCIs. Specific suggestions were proposed as below.
First, for small-scale MCIs, the current emergency health resources were enough to meet medical demands. However, promoting the efficiency of organization and command can greatly improve the timeliness of prehospital time and decrease mortality. For large-scale MCIs, improving the efficiency of organization and command can obviously improve the timeliness of the best stages of prehospital and hospital rescues, which would decrease the possibility of delay and mortality. For super-large-scale MCIs, improving the efficiency of organization and command could not play a role, which indicated that the key to improve medical rescue was to increase the amount of emergency health resources. The utilization rate of health resources and the efficiency of medical rescue can be improved only after meeting the medical demand of such super-large-scale MCIs.
Second, the timeliness of prehospital time can be improved by adjusting the number of ambulances and emergency medical staff. For small-scale MCIs, the current amount of ambulances and emergency medical staff were adequate enough to appropriately meet the medical demand; however, it is not advisable to reduce the current health resource allocation. For large-scale MCIs, increasing the number of ambulances within 24 hours and emergency medical staff within 16 hours can shorten prehospital time and decrease mortality. However, it was appropriate to evacuate some ambulances and emergency medical staff transferred temporarily to avoid the waste of health resources after 24 hours. For super-large-scale MCIs, due to the extreme shortage of emergency health resources, the current intervention scenarios cannot reach the critical point of improving efficiency of medical rescue. However, notably, it was significant to increase the number of emergency medical staff dramatically, which could decrease mortality and substantially affect triage and on-site first-aid time.
There are two limitations of this study. First, the model was based on MCIs caused by non-natural disasters, which somewhat restricts its application range. Second, to simplify the model, the injury condition of casualties was abstracted into the severity of injury, with other injury characteristics not considered. Both of these limitations will be addressed in future studies.
Conclusion
The keys to decrease the mortality of MCIs were shortening the prehospital time and improving the efficiency of organization and command. For different scales of MCIs, emergency medical rescue scenarios should be adjusted according to the medical demand. For small-scale MCIs, improving the utilization rate of health resources was important in decreasing mortality. For large-scale MCIs, increasing the number of ambulances and emergency medical professionals was the core to improve the timeliness of prehospital rescue and decrease mortality. For super-large-scale MCIs, the premise of shortening the prehospital time and improving the efficiency was to significantly increase health resources.
Acknowledgments
This study was supported by National Natural Science Foundation of China (71233008, 91224005, and 71774167), Joint Research Project of Major Disease of Shanghai Health System (2013ZYJB0006), and the Major Project in the “12th Five-Year Plan” of the People’s Liberation Army (AWS12J002).
Author contributions
WY, YL, CH, XL, HC, CX, and LZ jointly completed this study. WY, YL, and CH contributed equally to this research. WY made substantial contributions to conception and design, establishing the model, intervention experiments, interpretation of results, drafting the manuscript, and revising it critically for important intellectual content. YL and CH made substantial contributions to conception and design, model validation, interpretation of results, and drafting the manuscript. HC and CX were involved in data collection and intervention experiments. LZ made substantial contributions to conception and design. All authors contributed toward data analysis, drafting and critically revising the paper and agree to be accountable for all aspects of the work.
Disclosure
The authors report no conflicts of interest in this work.
References
Carles M, Levraut J, Gonzalez JF, Valli F, Bornard L. Mass casualty events and health organisation: terrorist attack in nice. Lancet. 2016;388(10058):2349–2350. | ||
Haverkort J, De Jong M, Foco M, et al. Dedicated mass-casualty incident hospitals: an overview. Injury. 2017;48(2):322–326. | ||
Yu M, Lv Q, Ding H, et al. Evaluation of blast injury patients from the 2015 Tianjin explosions in China. Burns. 2016;42(5):1133–1140. | ||
Chen SY, Chaou CH, Ng CJ, et al. Factors associated with ED length of stay during a mass casualty incident. Am J Emerg Med. 2016;34(8):1462–1466. | ||
Hang H, Jianan W, Chunmao H. Experience in managing an urban massive burn incident: the Hangzhou bus attack on 5 July 2014. Burns. 2016;42(1):169–177. | ||
Doughty H, Glasgow S, Kristoffersen E. Mass casualty events: blood transfusion emergency preparedness across the continuum of care. Transfusion. 2016;56(S2):S208–S216. | ||
Castro Delgado R, Naves Gómez C, Cuartas Álvarez T, Arcos González P. An epidemiological approach to mass casualty incidents in the Principality of Asturias (Spain). Scand J Trauma Resusc Emerg | ||
Baidu Baike [webpage on the Internet]. 9.27 Shanghaimetro Line Ten Accident. 2011. Available from: http://baike.baidu.com/link?url=6swJ80b-xXmQtvMclvNupeY2U-0okDGiJZHDP77GoXZWtkss2ODPz6KVOH9XB4tkx7K4FgNEWA6ZFx7WGvPkMqREfmjjlh3BhSqodFdNm0LPzva_a1FZTR2Arlc2TzcUfGZu19ys4hKSq3Wj4iQRWz9lIZeRbYlbd7YaI-gTSWdynJLdTIivPb6kvIvvTCtHiiRbpYTZCOlLCr8sCpvQvjNWMJeThItgqfpACivWWkXq3AWdSXaXKCLfSySTWfslbsOwJdGEspKQAl7aGVTSM2Slu_ib_p2PHQsSb3M9nmTDm | ||
Baibu Baike [homepage on the Internet]. 12.31 Shanghai Bund Stampede Accident. 2015. Available from: http://baike.baidu.com/link?url=m0qOae-BtTZejpmaK6MPvp6f-4TYtuK17jXTcX5ujFDgyI-e4ekJFC4Vq99Ro9knWK1Ql3eDFEnDHaRXhCXO28oVzLR0E8MAQBuwEOCVVjqS0wiGzc7YoG7zMtxJfefFfWVCJI02LfcbuZObGk9COgM4KSZk6igF_VZSL43y_2TMzd9C21woKAmD5etKB6zZPkGC2 | ||
Baidu Baike [homepage on the Internet]. August 2nd Kunshan Factory Blast Accident. 2014. Available from: http://baike.baidu.com/item/8·2昆山工厂爆炸事故?fromtitle=昆山爆炸事件&fromid= | ||
Baidu Baike [homepage on the Internet]. 8.12 Explosion Accident in Tianjin. 2015. Available from: http://baike.baidu.com/item/8·12天津滨海新区爆炸事故?fromtitle=天津爆炸事件&fromid=18883456. | ||
Zhao YJ [webpage on the Internet]. Shanghai-Chengdu Expressway Accident. 2016. Available from: http://news.e23.cn/content/2016-04-08/2016040800405.html. Accessed August 5, 2017. | ||
Shen WF, Jiang LB, Jiang GY, Zhang M, Ma YF, He XJ. Development of the science of mass casualty incident management: reflection on the medical response to the Wenchuan earthquake and Hangzhou bus | ||
Lewis AM, Sordo S, Weireter LJ, et al. Mass casualty incident management preparedness: a survey of the American College of Surgeons Committee on Trauma. Am Surg. 2016;82(12):1227–1231. | ||
Shalhoub AAB, Khan AA, Alaska YA. Evaluation of disaster preparedness for mass casualty incidents in private hospitals in Central Saudi Arabia. Saudi Med J. 2017;38(3):302. | ||
Pinkert M, Bloch Y, Schwartz D, et al. Leadership as a component of crowd control in a hospital dealing with a mass-casualty incident: lessons learned from the October 2000 riots in Nazareth. Prehosp | ||
Severance HW. Mass-casualty victim “surge” management. Preparing for bombings and blast-related injuries with possibility of hazardous materials exposure. N C Med J. 2002;63(5):242–246. | ||
Paturas J, Smith D, Smith S, Albanese J. Collective response to public health emergencies and large-scale disasters: putting hospitals at the core of community resilience. J Bus Contin Emer Plan. | ||
Ganz A, Schafer JM, Yang Z, Yi J, Lord G, Ciottone G. Evaluation of a scalable information analytics system for enhanced situational awareness in mass casualty events. Int J Telemed Appl. 2016;2016:10. | ||
Arcos González P, Castro Delgado R, Cuartas Alvarez T, et al. The development and features of the Spanish prehospital advanced triage method (META) for mass casualty incidents. Scand J Trauma | ||
Matsumoto H, Motomura T, Hara Y, et al. Lessons learned from the aeromedical disaster relief activities following the great East Japan earthquake. Prehosp Disaster Med. 2013;28(02):166–169. | ||
Omori K, Ohsaka H, Ishikawa K, et al. Introduction of a physician-staffed helicopter emergency medical service in eastern Shizuoka prefecture in Japan. Air Med J. 2014;33(6):292–295. | ||
Ishikawa K, Jitsuiki K, Ohsaka H, et al. Management of a mass casualty event caused by electrocution using doctor helicopters. Air Med J. 2016;35(3):180–182. | ||
The State Council [webpage on the Internet]. The Main Points of Working Plan of the State Council. 2005. Available from: http://www.gov.cn/zhengce/content/2008-03/28/content_1827.htm. | ||
The State Council [webpage on the Internet]. Formulation and Revision Framework of Emergency Plans for Public Events. 2004. Available from: http://www.gov.cn/zhengce/content/2008-03/28/ | ||
Hu X, Hu H, Yao L, Cao Y, He YR, Peng LY. Application of the Sacco triage method for trauma patients in Wenchuan earthquake. Chin J Emerg Resusc Disaster Med. 2016;11(10):949–952. | ||
Stephen L. Virtual reality and real-time simulation training: compare two simulation tools for assessing massive casualty triage ability. Chin J Emerg Resusc Disaster Med. 2016;10(8):752–753. | ||
Ning Y, Liu MS, Hou ZC, Meng YF, Liu WW. Pre-hospital triage and treatment of batch burns in emergencies. J Chin Phys. 2012;14(005):647–648. | ||
Deng D, Chen C, Tao J, et al. Application strategy of sonography in mass casualty incidents. J Mil Surg Southwest China. 2009;11(3):383–384. | ||
Körner M, Krötz MM, Wirth S, et al. Evaluation of a CT triage protocol for mass casualty incidents: results from two large-scale exercises. Eur Radiol. 2009;19(5):1867–1874. | ||
Hao ZG, Chen F, Cao CX, Song LX, Wu ZD, Meng QY. Medical rescue strategies of massive casualty incidents. China J Emerg Resusc Disaster Med. 2010;5(5):433–434. | ||
Hupert N, Hollingsworth E, Xiong W. Is overtriage associated with increased mortality? Insights from a simulation model of mass casualty trauma care. Disaster Med Public Health Prep. 2007;1(S1):S14–S24. | ||
Zhang HQ, Zhou GT, Zhang Y. Disaster Medicine. Beijing: Beijing Medical University and Peking Union Medical University Press; 1993. | ||
Shanghai Medical Emergency Center [webpage on the Internet]. Introduction of Shanghai Medical Emergency Center. 2015. Available from: http://www.sh120.sh.cn/jjzx/n3/n12/u1ai435.html. | ||
Yu W, Li M, Ge Y, et al. Transformation of potential medical demand in China: a system dynamics simulation model. J Biomed Inform. 2015;57:399–414. |
 © 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.