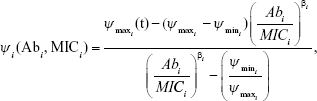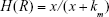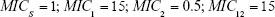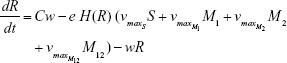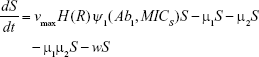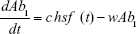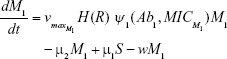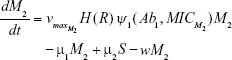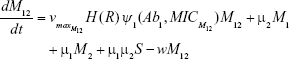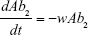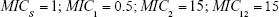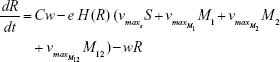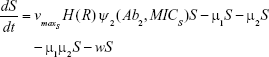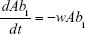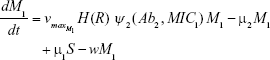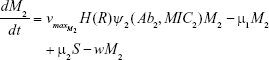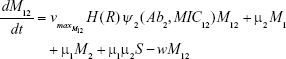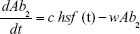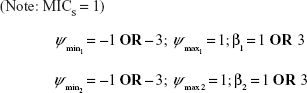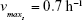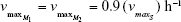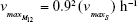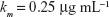Pharmacodynamic considerations of collateral sensitivity in design of antibiotic treatment regimen

Introduction

The impending era of ubiquitous antibiotic resistance is engendering an urgent search for new therapeutics as well as antibiotic stewardship strategies. Clinical strains have recently been isolated that are completely pan resistant – resistant to all available antibiotics. In lieu of new drugs or vaccines, the optimization of current therapeutic regimens is critical to continued treatment success. Stewardship approaches incorporating such considerations would ideally reduce the risk of within-host resistance development, thus minimizing endemic levels of such strains in the community.

The concept of collateral sensitivity (CS) was already described in the 1950s, when Bryson and Szybalski¹ observed that an Escherichia coli strain became hypersensitive to polymyxin B, upon acquiring chloramphenicol resistance. They speculated that this CS could be exploited clinically.

Recently, research teams have identified drug pairs that exhibit mutual collateral sensitivity (MCS) effects; evolution of resistance to drug A increases sensitivity to drug B and vice versa. MCS entails a reciprocal positive interaction between the 2 drugs. For the pathogens E. coli and Pseudomonas aeruginosa, a number of pairs of antibiotics have been identified which exhibit MCS to varying degrees.^2–5 Based on these studies, several groups have proposed antibiotic cycling of 2 antibiotics (eg, A → B → A → B → …, and derivatives thereof) to exploit MCS and to treat infections.² However, all but one study were limited to a single exposure to each antibiotic. While recent work has provided some understanding and potential mechanistic causes of such evolved sensitivity, it is unclear if CS is a universally applicable treatment consideration.

For P. aeruginosa infections in prophylactically exposed cystic fibrosis patients, 1) gentamicin-resistant strains are seen to become sensitive to penicillin due to a mutation in a 2-component system (pmrB), and, 2) nalC and mexZ mutations confer aminoglycoside sensitivity in β-lactam adapted strains.⁴ Data emerging from whole-genome sequencing of such isolates points to the need for a thorough exploration of the pharmacodynamic features of such treatment regimen where the CS strategy is employed. Roemhild et al⁶ cycled 2 antibiotics at a time in a morbidostat, an in vitro continuous-flow model. The morbidostat maintains a population density below a desired threshold by administration of bolus doses of antibiotic at specified optical densities. While a clever and useful device amenable to control and automation, for the potential clinical application, it trivializes the pharmacodynamics and greatly simplifies the underlying modeling. In this case, their model shows rapid ascent of double mutants and, experimentally, they find this in most cases. In addition to this, Nichol et al⁷ recently presented a combinatorial model describing the evolutionary limitations of CS strategy focusing on drugs with the same molecular target, cell wall synthesis. They concluded that “collateral sensitivity is contingent on the repeatability of evolution.”

Theoretical models can guide the testing and implementation of this cycling strategy, considering the evolutionary trends toward amplification of resistant clones during sequential monotherapies. Using simulated treatment protocols, the plausibility of CS-derived treatment regimens can be evaluated in silico and optimized in vivo. In this way, the implications for resistance development and the endemic fixation of these alleles can be assessed in “real time” before in vivo testing.

In this manuscript, we analyze the population dynamics of antibiotic cycling with the goal of clinical utility. We utilize clinically relevant parameters for presenting infections, high bacteria densities, and antibiotic dosages, in line with current treatment protocols.⁸ These models combined with pharmacokinetic (PK)/pharmacodynamic (PD) experiments would guide the clinical applicability of this proposed new treatment paradigm. Our model explicitly incorporates PK/PD parameters for individual strains, their mutation rates, and bacterial fitness effects. Our model implicitly accounts for immune control of bacterial density. We examine the sequential application of 2 drugs, A → B, each exhibiting different PD characteristics, to a hypothetical infection and estimate the rates of resistance ascent or population decline for single and multiply resistant clones in the simulated patient. The simulation results provide a foundation for validating this treatment framework. Time to clearance (of a hypothetical bacterial infection) represents the positive end of the scale, and time to fixation, T_fix, the negative end which the study focuses on for convenience. The presented framework is well-grounded in the underlying ecological, evolutionary, and pharmacological theory driving CS and allows us to study the efficacy of treatment achievable under such a regimen.

Current examples and proposals of MCS are for 2-drug cycling, and we formulated our original model to study this. It is not only applicable to antimicrobial chemotherapy but also to cancer chemotherapy where investigators have been studying treatment strategies of various cancers based on MCS considerations, although with mixed experimental results.⁹

Materials and methods

We constructed a compartment model where a susceptible population of bacteria, S, was exposed successively to 2 antimicrobial drugs, A1 and A2, and simulated treatment over a period of 10 days in most cases, and longer where necessary. All strains compete for a limited nutrient and grow at their respective maximum rates in the absence of antibiotic pressure. Resistance confers a fitness disadvantage of 10% for singly resistant mutants with a multiplicative factor of 10% per additional resistance mutation(s). The PK is provided by an in vitro kinetic model or chemostat¹⁰ at a rate mimicking human glomerular filtration rate (GFR). The at-times neglected PD is incorporated by modulating minimum growth rates relative to each strain’s respective minimum inhibitory concentration (MIC), as opposed to by the MIC alone. Collateral sensitivity is accounted for by switching the MIC of the relevant (preexposed) strain at periods corresponding to when the antibiotic is cycled, and CS is assumed to be instantaneous. A flow diagram representing the model is presented in Figure 1.

Figure 1 Flow diagram describing the population dynamics of sensitive (S) bacteria exposed to antibiotics and cells resulting from mutation/selection of resistance against antibiotic 1 (M1), antibiotic 2 (M2), or both (M12). Notes: Rates of mutation are independent of each other, here described by μ1 and μ2, and derived from Lee et al.11 The rate at which double resistant mutants arise is a of the individual mutation rates μ1 and μ2.

Treatment model description

Our treatment protocol consists of exposing a sensitive population of N₀=2×10⁸ CFU mL⁻¹ of bacteria to each antibiotic, as described. We set the flow rate to 0.2 L h⁻¹ and assume a basal mutation rate, μ, of 3.9×10⁻¹⁰ nucleotide⁻¹ generation⁻¹, a conservative estimate as compared to the estimated range of μ.¹¹ A single mutation is assumed to be sufficient to induce clinically significant resistance, and there is an insignificant likelihood of reversion to full sensitivity.¹²

For sensitive cells, the MIC is set to 1 μg mL⁻¹. When applying drug A, or drug B, the MIC of the cells resistant to drug B or drug A, respectively, is set to 0.5 μg mL⁻¹ and these cells are thus more sensitive than the original population. The MIC of resistant cells is always set at 16 μg mL⁻¹ prior to switching when antibiotic is cycled. We assume a 10% reduction in fitness by imposing a penalty on maximum growth rate. For each resistance “acquisition,” an additive fitness penalty is incurred with the triply resistant isolate being least “fit.”

Antibiotics are pulsed at concentration, c μg mL⁻¹ (3≤ c ≤10) into the chemostat for 1 hour, followed by 5 hours of medium alone. This is repeated 4 times per day and the antibiotic switched daily (Pharma 7 days, 6 hours). The function hsf (t), attaining values 0 or 1 implements this protocol in the model (‘Heaviside step function’). The PD responsiveness of the exposed population to a given antibiotic concentration concentration is reflected in the Hill coefficient, β, which defines how “rapidly” the maximum efficacy is attained; the sensitivity of the bacterial population at concentrations close to the MIC.

We simulated MCS-guided treatment with daily, and 3 day cycling between antibiotics.

We followed each population throughout the treatment period and estimated time to clearance or the time to fixation of multiple drug resistance for either 2 or 3 drug rotations. The inhibitory effect of each antibiotic is reflected in the term, Ψ_min, which also represents the maximal kill rate for each antibiotic. Values for β and Ψ_min are derived from experimental studies on E. coli and Staphylococcus aureus.^13,14 We modeled the intrinsic growth of the population using a Monod model with resource conversion efficiency, e =5×10⁻⁷ μg, and a Monod constant, κ of 0.25 μg mL⁻¹.¹⁵ Initially, there were no resistant isolates and we assumed that the bacteria do not engage in horizontal gene transfer, a critical assumption for a fair assessment of CS.

Shown herein is the coupled system of nonlinear differential equations which describes the treatment regimen using 2 antimicrobials. We carefully simulated solutions using Matlab. The system was stiff for some parameter values, and we utilized a stiff solver in such cases.

Mathematical modeling

For all anitbiotics, we use the pharmacodynamic function taken from Regoes et al.¹³

(1)

where i represents each respective antibiotic (in this iteration, 1 or 2)

(2)

Antibiotic 1

Parameters for dosing Ab₁

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Antibiotic 2

Parameters for dosing Ab₂

(10)

(11)

(12)

(13)

(14)

(15)

(16)

where

R = Chemostat resource concentration

C = Resource Reservoir concentration

Ab₁ = Antibiotic 1 concentration

Ab₂ = Antibiotic 2 concentration

S = Sensitive cells

M₁ = Resistant mutants to Ab₁

M₂ = Resistant mutants to Ab₂

M₁₂ = Double-resistant mutants

μ₁ = Mutation rate (to Ab₁)

μ₂ = Mutation rate (to Ab₂)

With initial chemostat resource concentration, R₀=100 μg mL^–1, and sensitive bacteria, S₀ = 2×10⁸ CFU mL^–1

Chemostat parameters

w = 0.2 mL h−1			{flow rate},
C = 500 μg mL−1			{resource reservoir}
Abi = 3μg mL−1 h−1 OR 10 μg mL−1 h−1			{per hour dosed antibiotic}
(Note: MICS = 1)
μ1 = 3.9 × 10−10   bp−1 h−1			{spontaneous mutation rate => to Ab1}
μ2 = 3.9 × 10−10   bp−1 h−1			{spontaneous mutation rate => to Ab2}
Parameter values
e = 5 × 10−7 μg			{per cell division glucose requirement15}
			{maximum growth rate of sensitive cells S}
			{maximum growth rate singly resistant cells}
			{maximum growth rate doubly resistant cells}
			{Monod constant, taken from Levin et al15}

Results

In silico assessment of 2 drug cycling

We simulated treatment with 2 antimicrobials exhibiting varying PD parameters and encompassing both bacteriostatic antibiotic (Static) and bactericidal (Cidal) drug types (Table 1 and “Materials and methods” section). We considered both daily cycling and 3-day cycling of each antibiotic. We defined the time to fixation, T_fix, as the time between first application of drug 1 and the time at which the double-resistant strain exceeded 0.9 N₀. The simulation results are summarized in Table 1 and displayed in Figure 2.

Table 1 Two antibiotic exposure simulations with daily cycling between antibiotic 1 and antibiotic 2 for 1 day and 3 day cycling protocols Notes: Cidal denotes a bactericidal antibiotic, while Static denotes a bacteriostatic antibiotic. We report resistance fixation Tfix in each simulation.

Figure 2 Selected simulations of our mathematical model showing changes in resource and antibiotics concentrations as well as population densities of sensitive, single antibiotic resistant, and double resistant cells. Notes: Each panel (A–D) represents different runs for input antibiotic concentrations of 3 μg mL−1 (A: β =1, Static/Static; B: β =3, Static/Static; C: β =1, Cidal/Cidal; D: β =3, Cidal/Cidal). Represent the population densities of doubly resistant cells → Tfix for runs (A–D), respectively. C denotes a bactericidal antibiotic, while S denotes a bacteriostatic antibiotic.

For low antibiotic dosing (~3× MIC of sensitive cells), fixation of double mutants, ie, resistance to both applied antibiotics occurred rapidly, T_fix ranging between 67 and 115 hours. This occurred despite the increased susceptibility imposed by CS theory. The fixation of double-resistant strains is seen to be invariable, although it takes 50% longer when drugs are cycled every 3 days than when cycling daily. The use of drugs with smaller Hill coefficients (β) leads to a 25% delay in fixation. Less significant are the differences between the various combinations of S and C drugs. For drugs with small Hill coefficients, however, there was a 5% delay in fixation when 1 static drug was used and a further 5% delay when both cycled drugs were bacteriostatic.

For moderate to high dosing schemes (~10× MIC of sensitive cells), for drugs having large β, doubly resistant mutants fixated rapidly, within 4 days of treatment initiation. This was not the case for drugs with small β values with which resistance only emerged (and fixated) long after a traditional clinical treatment regimen was completed, ie, >7–10 days. T_fix also decreased when using 2 bactericidal drugs as compared to other combinations of bacteriostatic and bactericidal drugs. The best strategy of all from our simulations was the use of 2 bacteriostatic drugs with a low β, while cycling them every 3 days. Under these conditions, no resistance was observed for any conceivable infection treatment duration, which we interpret as meaning that such regimen with MCS guiding protocol may actually inhibit the development of resistance.

Lastly, we noted that significant short duration population spikes (>10⁵ CFU mL⁻¹) occurred for some singly resistant strains.

Discussion

The emerging crisis that is pan-antibiotic resistance, compounded by a dearth of new antibiotics in the development pipeline,¹⁶ is necessitating new approaches to chemotherapy to minimize resistance emergence and dissemination. Many clinical treatment strategies have been proposed, ranging from combinatorial therapy to antibiotic cycling incorporation in the treatment of everyday infections in order to mitigate resistance emergence. Antibiotic cycling can be implemented either at the level of individual patients or the institutional unit. Earlier modeling studies of unit cycling cast doubts on the utility of this strategy¹⁷ and results of hospital trials have been mixed.

The MCS approach is an exciting treatment option, but multiple-cycle testing with clinically relevant PK/PD consideration has not been explored. Our mathematical model allows us to do precisely this, focusing on the PD properties relevant to treatment of a hypothetical infection. Our modeling strategy not only considers the classical MIC but also the dose responsiveness of a population of sensitive and resistant bacteria in a resource-limited setting. This provides a broader perspective than the usual 1 parameter, MIC, summary on the PD.

Several drug pair combinations have been identified as exhibiting MCS as earlier stated. Results from studies utilizing whole genome sequencing have identified 2 possible mechanisms steering MCS: 1) intragenic suppression of resistance,⁷ and 2) epistasis-derived reversal of resistance (toward the other drug).² These are based on both the mutation target size and the breadth of the path each adaptive walk has traversed. Intragenic suppression is limited by the smaller number of mutations that can lead to an MCS phenotype for a related antibiotic, while epistatic suppression is more dependent on an underlying genetic diversity. These are also discussed in a study by Nichol et al,⁷ and the observed saddlepoint in their published evolutionary landscape points to potential treatment failure; evolutionary unpredictability as such is not considered herein. These only serve to bolster the importance of our comprehensive PD study.

PD properties of antibiotics are broadly delineated as Cidal or Static for ease of pharmacological understanding. Most Static drugs are weakly cidal and while Cidal drugs are often preferred to Static drugs; in immunocompetent patients, there is no advantage in using the former. From our simulations, it appears that when exploiting MCS, the Static drugs are superior to their cidal counterparts, as they inhibit significant expansion of resistant strains. To our knowledge, this is the first report or observation of such, emerging albeit from an in silico study.

As presented in the “Results” section, we observe the rapid fixation of resistance in all cases of low drug concentration exposure, underlining the importance of adequate dosage. The large population sizes commonly associated with infections, also considered in our study, would require an immunocompetent host (patient) to clear. At first glance, our model lacks both innate and adaptive immunity (approached in a study by Gjini et al¹⁸), but the innate immunity is implicit in the form of resource concentration limitation on population size.

From the estimates of T_fix, the single factor most significant in the early fixation of multiple resistance using this MCS protocol is the cycling period (cv 67 vs 110 hours for 1 day cycling and 3 day cycling, respectively). Following this is the effect of the Hill coefficient, β, on T_fix which, in line with Day and Read,¹⁹ challenges the idea that increased clearance rates minimize the selection and fixation of resistant isolates. The increased selective pressure imposed by higher-order Cidal drugs leads to a more rapid fixation of resistance in the population. Our model explains this from a nutrient competition perspective; as antibiotic 2 is being applied, the killing of the sensitive cells and those resistant to antibiotic 1 results effectively in reducing the total population density, and thus competition is relaxed.

This is also true for the other antibiotics, and evolution of doubly resistant mutants is facilitated by the large population sizes being acted upon by the imposed (conservative) mutation rate in our model (Figure 2). Once doubly resistant, this CS is lost, and overall fitness of the population is maximized under (either Ab₁ or Ab₂) antibiotic pressure.

It is known that the efficacy of beta lactam antibiotics is highest at concentrations around 5 times the MIC, and the results obtained from our low-dose simulations are thus interesting for this highly clinically utilized class of antibiotics. The PD parameter β describes the sensitivity of the antibiotic to changes proximal to the point of inflection (zero growth) in the graph of the Hill function (explained in treatment model description). This plays a vital role in the success of MCS-guided treatment regimen although it is not evident á priori (Figure 3). As is seen upon replotting the data to reflect the effect of β on our estimate of efficacy, the fixation time for Cidal drugs in particular is heavily dependent on the drug dosage especially for the 3 day (3 d) cycling protocol. These are strong indicators of the importance of drug choice under such treatment regimen considerations.

Figure 3 Categorical plot showing the effect of parameter values β and ψmin on time to fixation, Tfix, for 2 drug concentrations; 3 μg mL−1 (A and C) or 10 μg mL−1 (B and D) of combinations of Cidal and Static drugs (C and S on x-axes) were simulated with β =1 (red) or β =3 (blue) and cycled either every day (A and B) or every 3 days (C and D). C denotes a bactericidal antibiotic, while S denotes a bacteriostatic antibiotic.

In vivo, the immune system works hand in hand with antibiotics to clear the infection. In some of our simulations, the single and double mutants remain at low enough densities to be easily cleared by circulating immune cells in a hypothetical patient. However, when fixation of double mutants occurs within a few days, the likelihood of treatment failure would, by definition, increase. Even in cases where fixation does occur, the immune system, unaffected by the antibiotic resistant state of the population, may still clear the infection. As such, our model only serves as a cautionary tale; heterogeneity in immunity and an immunocompromised state could exacerbate the likelihood of treatment failure, as would antimicrobial heteroresistance, inoculum effects, and high frequency of resistant bacteria in the original infection.

In addition, horizontal gene transfer confounds the model’s predictability as the rate of plasmid-mediated resistance transmission, especially conjugable plasmids, is considerably higher than the replication-dependent vertical propagation of point mutations. We neither consider plasmid-based transmission of antimicrobial resistance genes nor do we include any resistant mutants initially, only considering de novo mutations conferring resistance. These mutations we assume occur independently of one another. Under continuous antibiotic exposure, selection drives the system toward a fitness maximum through resistance compensation which is favored over reversion.¹²

The modeling framework we present in this manuscript treats 2 drug cycling but has already been extended to 3 drug cycling in anticipation of triplet combinations that may be identified in due course. Before clinical deployment however, the utility of MCS must be explored experimentally, rationalized physiologically, and further tested for generality. Mathematical models of this sort will play a crucial role in establishing the applicability and suggesting modifications to this and other proposed treatment regimen.

Acknowledgments

The authors acknowledge the KITP program on Ecology and Evolutionary Biology 2017 (NSF grant no. PHY17-48958, NIH grant no. R25GM067110, and the Gordon and Betty Moore Foundation grant no. 2919.01). This work was supported by a Swedish Research Council Junior Investigator Grant # 621-2012-3564 to KIU.

Disclosure

The authors report no conflicts of interest in this work.

---

References

1.		Bryson V, Szybalski W. Microbial selection. Science. 1952;116(3003):45–51.
2.		Imamovic L, Sommer MO. Use of collateral sensitivity networks to design drug cycling protocols that avoid resistance development. Sci Transl Med. 2013;5(204):204ra132.
3.		Pal C, Papp B, Lazar V. Collateral sensitivity of antibiotic-resistant microbes. Trends Microbiol. 2015;23(7):401–407.
4.		Jansen G, Mahrt N, Tueffers L, et al. Association between clinical antibiotic resistance and susceptibility of Pseudomonas in the cystic fibrosis lung. Evol Med Public Health. 2016;2016(1):182–194.
5.		Oz T, Guvenek A, Yildiz S, et al. Strength of selection pressure is an important parameter contributing to the complexity of antibiotic resistance evolution. Mol Biol Evol. 2014;31(9):2387–2401.
6.		Roemhild R, Barbosa C, Beardmore RE, Jansen G, Schulenburg H. Temporal variation in antibiotic environments slows down resistance evolution in pathogenic Pseudomonas aeruginosa. Evol Appl. 2014;8(10):945–955.
7.		Nichol D, Rutter J, Bryant C, et al. Collateral sensitivity is contingent on the repeatability of evolution. bioRxiv. 2017:1–14.
8.		König C, Simmen HP, Blaser J. Bacterial concentrations in pus and infected peritoneal fluid – implications for bactericidal activity of antibiotics. J Antimicrob Chemother. 1998;42(2):227–232.
9.		Pluchino KM, Hall MD, Goldsborough AS, Callaghan R, Gottesman MM. Collateral sensitivity as a strategy against cancer multidrug resistance. Drug Resist Updat. 2012;15(1–2):98–105.
10.		Chao L, Levin BR, Stewart FM. A complex community in a simple habitat: an experimental study with bacteria and phage. Ecology. 1977;58(2):369–378.
11.		Lee H, Popodi E, Tang H, Foster PL. Rate and molecular spectrum of spontaneous mutations in the bacterium Escherichia coli as determined by whole-genome sequencing. Proc Natl Acad Sci U S A. 2012;109(41):E2774–E2783.
12.		Andersson DI, Hughes D. Antibiotic resistance and its cost: is it possible to reverse resistance? Nat Rev Microbiol. 2010;8(4):260–271.
13.		Regoes RR, Wiuff C, Zappala RM, Garner KN, Baquero F, Levin BR. Pharmacodynamic functions: a multiparameter approach to the design of antibiotic treatment regimens. Antimicrob Agents Chemother. 2004;48(10):3670–3676.
14.		Levin BR, Udekwu KI. Population dynamics of antibiotic treatment: a mathematical model and hypotheses for time-kill and continuous-culture experiments. Antimicrob Agents Chemother. 2010;54(8):3414–3426.
15.		Levin BR, Stewart FM, Chao L. Resource-limited growth, competition and predation: A model and experiment studies with bacteria and bacteriophage. Am Naturalist. 1977;111(977):3–24.
16.		Martens E, Demain AL. The antibiotic resistance crisis, with a focus on the United States. J Antibiot (Tokyo). 2017;70(5):520–526.
17.		Levin BR, Bonten MJ. Cycling antibiotics may not be good for your health. Proc Natl Acad Sci U S A. 2004;101(36):13101–13102.
18.		Gjini E, Brito PH. Integrating antimicrobial therapy with host immunity to fight drug-resistant infections: classical vs adaptive treatment. PLoS Comput Biol. 2016;12(4):e1004857.
19.		Day T, Read AF. Does high-dose antimicrobial chemotherapy prevent the evolution of resistance? PLoS Comput Biol. 2016;12(1):e1004689.