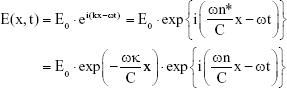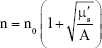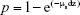Back to Journals » International Journal of Nanomedicine » Volume 11
New optical sensing technique of tissue viability and blood flow based on nanophotonic iterative multi-plane reflectance measurements
Authors Yariv I, Haddad M, Duadi H, Motiei M, Fixler D
Received 5 August 2016
Accepted for publication 2 September 2016
Published 11 October 2016 Volume 2016:11 Pages 5237—5244
DOI https://doi.org/10.2147/IJN.S119130
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Thomas Webster
Inbar Yariv,1 Menashe Haddad,2,3 Hamootal Duadi,1 Menachem Motiei,1 Dror Fixler1
1Faculty of Engineering and the Institute of Nanotechnology and Advanced Materials, Bar Ilan University, Ramat Gan, Israel; 2Sackler School of Medicine, Tel-Aviv University, Tel-Aviv, Israel; 3Mayanei Hayeshua Medical Center, Benei Brak, Israel
Abstract: Physiological substances pose a challenge for researchers since their optical properties change constantly according to their physiological state. Examination of those substances noninvasively can be achieved by different optical methods with high sensitivity. Our research suggests the application of a novel noninvasive nanophotonics technique, ie, iterative multi-plane optical property extraction (IMOPE) based on reflectance measurements, for tissue viability examination and gold nanorods (GNRs) and blood flow detection. The IMOPE model combines an experimental setup designed for recording light intensity images with the multi-plane iterative Gerchberg-Saxton algorithm for reconstructing the reemitted light phase and calculating its standard deviation (STD). Changes in tissue composition affect its optical properties which results in changes in the light phase that can be measured by its STD. We have demonstrated this new concept of correlating the light phase STD and the optical properties of a substance, using transmission measurements only. This paper presents, for the first time, reflectance based IMOPE tissue viability examination, producing a decrease in the computed STD for older tissues, as well as investigating their organic material absorption capability. Finally, differentiation of the femoral vein from adjacent tissues using GNRs and the detection of their presence within blood circulation and tissues are also presented with high sensitivity (better than computed tomography) to low quantities of GNRs (<3 mg).
Keywords: Gerchberg-Saxton, optical properties, gold nanorods, blood vessel, tissue viability, reflectance, scattering
Introduction
Extracting optical parameters of turbid medium (eg, tissue) by light transmittance and reflectance signals is of great interest and has many applications in the medical world, life science, material analysis and biomedical optics.1 Recovering tissues’ optical properties, which regularly change according to their physiological state, has been presented and applied for diagnosis purposes such as tumor detection,2,3 optical imaging of brain tissue composition and physiology4 and DNA and protein changes in human breast tissue.5 The reemitted light from irradiated tissue is affected by the light’s interaction with the tissue components and contains the information about the tissue structure and physiological state. This information can be extracted from the reemitted light profile using analytical models for photon migration within physiological substances (eg, diffusion reflection,6 random walk7 and radiative transfer equation).8 The field of light–tissue interactions has been studied extensively with new techniques emerging constantly,9–13 where each technique has its own advantages as well as limitations and disadvantages. However, Lister et al14 have reviewed some of the leading analyses of human skin’s optical properties, by presenting values of absorption and reduced scattering coefficients (μa and μs′ respectively) published in the literature,15–23 both in vitro and in vivo, and their large dynamic range, concluding that further research should be done.
We have previously presented a theoretical and practical model (ie, the iterative multi-plane optical property extraction (IMOPE)) for reconstructing the optical properties of tissues by computing the standard deviation (STD) of the remitted light phase based on transmission measurements.24,25 In former publications, the transmission based IMOPE has been applied for the detection of organic nanoparticles within tissues in order to promote the use of topical medications instead of injections24–26 and for detecting the quantitative signature of milk content (lactose and milk proteins).25 However, transmission techniques are limited by the optical penetration depth (δ), which has to be greater than the sample thickness in order to receive the reemitted light signal, making them less suitable for thick and highly scattering media, such as tissues, and clearly not practical for in vivo measurements. The reflectance based IMOPE presented in this research uses a simple experimental setup composed of a laser and CMOS camera in order to detect the reflected light phase changes. The theoretical model is based on Gerchberg-Saxton (G-S) algorithm27 which is known for its phase retrieval and beam shaping applications for image reconstruction.28,29 The algorithm uses known light intensity images at known distances and the propagation of light between them in order to reconstruct the light phase that was lost once the image was captured. We, however, have demonstrated a novel concept of examining the light phase STD, not the phase itself, in order to extract the optical properties and thereby the desired information of tissues. Hence, following the phase reconstruction its STD is calculated and examined for extracting the tissues’ scattering properties.24,25 The STD together with the image location (which is known from the experimental setup) can provide the reduced scattering coefficient estimated value by a database.
As mentioned above the reemitted light phase from an irradiated substance, which is reconstructed by the iterative G-S algorithm, has a strong connection to its optical properties. When light, as an electromagnetic wave, propagates through a substance, it is affected by the substance’s optical properties and can be described as written below (Equation 1):
|
|
where k = ωn*/C is the wave vector, ω is the circular frequency, C is the speed of light in the vacuum and n* is the complex refractive index which is defined by: n* = n + i·κ, with n and κ being the real part and imaginary part of the refractive index respectively. Inserting k to Equation 1, we received an attenuated electromagnetic wave that accumulated phase changes as well (represented by the second exponent) which depend on the refractive index, n. The relation between n and the reduced scattering coefficient (μs′) can be written as follows (Equation 2):
|
|
where n0 is the refractive index of the medium and A is the proportionality factor related to particle size, wavelength and particle density and includes the anisotropy factor, g.30 Meaning that the reduced scattering coefficient is related to the light phase changes that occur while propagating through substances.
In this paper, the application of the new nanophotonics reflection based IMOPE on both ex vivo and in vivo experiments is presented. Ex vivo experiments were conducted on mice ears examining optical effect of thin tissue viability. In vivo experiments were conducted on mice, with gold nanorods (GNRs) intravenously injected, for examining the reflectance based IMOPE ability to differentiate the femoral vein from tissues in its environment following GNRs injection.
Materials and methods
IMOPE
The IMOPE model is composed of two parts that combine a tissue simulation (part 1) with an experimental setup for recording light intensity images for calculating the STD of the reemitted light phase based on G-S algorithm (part 2). The tissue simulation generates a database (ie, look up table) that connects the three main variables, the STD which is calculated in the IMOPE second part, the location within the irradiated tissue, Z which is known, and the reduced scattering coefficient, μs′.
Tissue simulation
In order to understand the influence of the tissue’s optical properties on the STD of the light phase, a MATLAB simulation was performed. The model is based on a more simplistic model31,32 where in an event of scattering the light direction is simply changed by cos−1 (g). Free space assumes propagation in the z direction, while direction changes are expressed in the phase of the electromagnetic field. While propagating a distance of dz, a change in the direction will create an added optical path of dz/g. In the reflection simulation the detector is located at the same side as the light source, both adjacent to the tissue. The tissue is divided into small slices (dz) and we assume that the light can only scatter in known positions which are separated by a distance dz where the light free space propagates.31,32 In the planes where the light can scatter, the probability (p) of each pixel (within a 1,025×1,025 matrix) to scatter was calculated according to Wang et al and Welch et al,33,34 as follows:
|
|
where μs is the scattering coefficient and can be described as: μs′/(1−g). If the light scatters in a specific pixel, the optical path is now dz/g, where g is defined as g = cosφ. Hence the additional phase due to the scattering is: 2πdz(1/g − 1)λ. Since the pixel size of the detector is 6 μm, and we assume that following a scattering event, the propagated light does not transfer to adjacent pixels, dz had to be smaller than the pixel size, hence we arbitrarily chose dz =5 μm.
Using these assumptions, the STD for different tissue thicknesses and different reduced scattering coefficients was calculated in order to create a look up table.
IMOPE algorithm
The algorithm used for reconstructing μs′ is described in Figure 1. In order to reconstruct the reemitted light phase,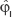 first a multiple measurement G-S algorithm is used with N intensity images, as described in Yariv et al,24 and T iterations. Then, as the phase
first a multiple measurement G-S algorithm is used with N intensity images, as described in Yariv et al,24 and T iterations. Then, as the phase 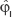 is an image of many pixels, with normal distribution, the phase’s STD is calculated. Given the tissue thickness Z, the estimated value for the reduced scattering coefficient can be extracted from the look up table (that was built as described previously).
is an image of many pixels, with normal distribution, the phase’s STD is calculated. Given the tissue thickness Z, the estimated value for the reduced scattering coefficient can be extracted from the look up table (that was built as described previously).
Experimental setup
The algorithm detailed in the previous section (IMOPE algorithm) uses light’s intensity images for reconstructing the reemitted light phase. In order to achieve that, a noninvasive reflection based experimental setup was designed. The setup is composed of a helium neon (He-Ne) gas laser with a wavelength of λ =632.8 nm and power of 3.4 mW, polarizers for optical clearing purposes,35,36 lens (focal length of fRef =75 mm) in order to focus the light beam and CMOS camera (DCC1545M, Thorlabs, Japan). The lens and camera were set on a micrometer plate for recording the light’s intensity images at different distances. The samples were held by a 3 axis micrometer stage for fine-tuning during experiments. The setup was built for light reflectance measurements as shown in Figure 2.
For each sample, the intensity images were recorded at multiple planes, where the distance between each two planes was the same. The recorded intensity images (1,025×1,025 pixels) were then processed by the algorithm, as explained in IMOPE algorithm section, using MATLAB in order to receive the STD of the sample.
GNRs preparation
GNRs were synthesized using the seed mediated growth method.37 Their size, shape and uniformity were characterized using transmission electron microscopy (TEM) and the resultant shape was 25×65 nm, with narrow size distribution (10%), TEM images are presented in Figure 3A.2,3,38 In order to prevent aggregation, to stabilize the particles in physiological solutions and to improve blood circulation time, a layer of polyethylene glycol (mPEG-SH, MW 5,000 g/mol) (creative PEGWorks, Winston Salem, USA) was conjugated to the GNR. A solution of GNRs suspended in cetyltrimethylammonium bromide (CTAB) (Sigma-Aldrich Co., St Louis, MO, USA) was centrifuged at 7,000 ×g for 30 minutes, decanted and resuspended in water to remove excess CTAB. mPEG (200 ml of 5 mM) was added to 1 mL of GNR solution. The mixture was stirred for a few hours at room temperature and was dialyzed for three days. The absorption spectrum of PEGylated GNR solution presented a strong peak at 645 nm, as can be seen in Figure 3.
Ex vivo experiments
Two nude mice (age 5 weeks) were anesthetized using 100 μL of a mixture of ketamine 10 mg/mL + xylazine 2 mg/mL injected intraperitoneally. A few days following anesthesia, the mice were sacrificed and for each one both ears were taken for measurements under room temperature. In order to examine thin tissues’ viability, the ears were divided into two groups: group 1 – two ears were measured at the same day and group 2 – two ears were measured after 6 days of being kept under 4°C refrigeration. Following these control measurements, for each group, 5 μL of aqueous 2 mM Methylene blue (MB) solution (Sigma-Aldrich Co.) was applied to the ears and reflection signals were measured again after 24 hours. The ears were placed in the experimental setup on a vertical polycarbonate mount fixed by Sellotape® (polypropylene-based tape). Three measurements of reflection signals were obtained from adjacent different segments of each ear.
In vivo experiments
A nude mouse (age 5 weeks) was anesthetized using 100 μL of a mixture of ketamine 10 mg/mL + xylazine 2 mg/mL injected intraperitoneally. The femoral vein was measured before (control) and after it was injected with 150 μL (20 mg/mL gold) of GNRs by tail vein injection in two time periods (t =0.25 h, 24 h postinjection). The tissues next to the femoral vein were measured postinjection as well, for investigating the GNR effect on the femoral vein environment. The mouse was laid on a flat surface with its inner thigh facing the laser; it was placed on the sample holder in the experimental setup and fixed to the polycarbonate mount, as shown in Figure 4. Computed tomography (CT) scanning was performed before GNRs injection to determine the CT baseline, as well as postinjection in two time periods (4 h and 8 days postinjection).
  | Figure 4 The experimental setup during in vivo measurements. |
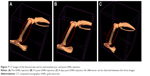
The CT scans were performed using a micro-CT scanner (Skyscan High Resolution Model 1176) with nominal resolution of 35 μm, 0.2 mm aluminum filter and tube voltage of 45 kV. Reconstruction was done with a modified Feldkamp47 algorithm using the SkyScanNRecon software accelerated by GPU.48 Ring artifact reduction, Gaussian smoothing (3%) and beam hardening correction (20%) were applied. Volume rendered three-dimensional images were generated using an RGBA transfer function in SkyScan CT-Volume (“CTVol”) software and in SkyScan CT-Voxel (“CTVox”) software. The contrast enhancement was quantitatively determined according to the differential contrast in CT numbers (in Hounsfield units), compared to that of the same mouse before injection. All CT scans were performed under appropriate anesthesia. Up to 8 days post-intravenous injection, mouse behavior was normal and without any evidence of toxicity.
This study received institutional approval from the Bar Ilan Institute for Nanotechnology and Advanced Materials Institutional Animal Care and Use Committee. All ex vivo and in vivo measurements were performed under appropriate anesthesia: the mice barrier-controlled facility followed the Bar Ilan’s Institute for Nanotechnology and Advanced Materials Animal Care and Use Committee guidlelines. The mice were inspected daily by the veterinarian, who handles the appropriate tests and treatment protocols, as required. All research protocols were followed closely by the veterinarian. All major procedures were performed in the surgical facilities using general anesthesia and standard, aseptic surgical techniques.
Results and discussion
Tissue viability examination
Ex vivo experiments were conducted according to the procedure detailed above for examining the effect of tissues at different states on the light phase STD. The computed STDs for group 1 (experiments were conducted on the same day as sacrifice, ie, day 0) and group 2 (experiments were conducted 6 days following sacrifice, ie, day 6) before and after applying MB (control and MB respectively) are presented in Figure 5 in the orange (control) and blue (MB) bars. The results in Figure 5 show a change in the STD when comparing the control tissue (orange bars) at day 0 and day 6, an 8% decrease in the STD (***P<0.001) indicating a change in the tissue composition that decreases the scattering properties of the tissue. An additional test was conducted on the tissues at their different states by applying MB and examining their effect on the light phase STD. The results presented in Figure 5 show that the STD decreases as the MB has a strong absorption ability. Hence less photons can be scattered resulting in a decreased reemitted light phase STD for both tissues. However, the decrease in the STD for the older tissue (day 6) is much smaller (0.05% with *P<0.05) than the one obtained for the tissue immediately following injection, ie, day 0 (0.15% with ***P<0.001).
Differentiation between femoral vein and its environment
GNRs have been used extensively as contrast agents and are very popular due to their physicochemical and anisotropic shape properties.39 They have previously been suggested as a great candidate for CT contrast agents with 5 mg injected GNRs being the detection threshold in mice.2,3,40,41 Wishing to differentiate the femoral vein from its environment and detect the blood flow effect on the light phase STD, GNRs were used as contrast agent and in vivo experiments were conducted. Figure 6A shows the irradiated mouse femoral vein during the in vivo experiments. The results for the femoral vein and adjacent tissue experiments post-GNRs injection (red and green bars, respectively) are presented in Figure 6B and were normalized to the STD value of the control measurements. The normalized computed STD of the femoral vein 0.25 h post-GNRs injections is 1.05±0.025 demonstrating the presence of GNRs within the femoral vein, as they increase the scattering properties of the femoral vein. However, 24 h later, the GNRs were mostly cleared from the blood circulation, resulting in the normalized STD (decrease back to approximately the control STD value (1.001±0.008)). This indicates the clearance of the GNRs from the femoral vein. Examining the tissues in the femoral vein environment, we have observed an increase in the normalized STD following GNRs injection (*P<0.05). The normalized STD, 15 minutes (0.25 h) postinjection, of adjacent tissues (green bar) is lower than the one measured in the femoral vein since tissues have lower scattering properties than blood vessels.14 In addition, the GNRs have yet to reach the tissues adjacent to the femoral vein (as some of the GNRs, while being cleared from the blood circulation, will diffuse into adjacent tissues) resulting in normalized STD of 0.865±0.005 (***P<0.001). Approximately, 24 h postinjection, the GNRs were cleared from the blood circulation and some were diffused into adjacent tissues resulting in a higher scattering ability which increases the STD, as shown in Figure 6B, to 0.89±0.006 (***P<0.001). The mouse was scanned before and after GNRs injection using CT (as described in Material and methods section).
The CT images pre- and 4 h and 8 days postinjection are presented in Figure 7A–C, respectively. When using CT scanning, in order to observe the GNRs in the image, the common injection amount is more than 5 mg,40,41 the injected GNRs in the presented experiments were only 3 mg. Therefore, looking at the CT images (Figure 7A–C), no differences can be observed between pre and post injection although, while using the reflectance based IMOPE the presence of the GNRs was observable.
Conclusion
Extracting optical properties of physiological substances (eg, tissues) has many applications and various techniques have been developed, as was described previously. Examination of tissues noninvasively can be achieved by different optical methods, practically all of which are based on light reflectance measurements. In the present paper, we have applied, for the first time, the reflectance based IMOPE for tissue optical properties extraction. The basics of the reflectance based IMOPE were described combining a simple experimental setup for recording light intensity images with an iterative G-S algorithm for reconstructing the reflected light phase and computing its STD. The results presented in this work show that the reflectance based IMOPE was able to differentiate between the viability of different tissues and their MB absorption capability by the computed reflected light phase STD. In addition, by combining a very small amount of injected GNRs with the IMOPE we were able to distinguish between the femoral vein and other tissues adjacent to it, obtaining a higher STD for the femoral vein, as was expected. The GNRs presence within the femoral vein and its environment during 24 h postinjection was detected as well. With the total quantity of injected GNRs being 3 mg, much less has been diffused to the femoral vein environment. The reflectance based IMOPE was applied successfully in the ex vivo and in vivo measurements detailed above, indicating significant potential in clinical medicine. Nonetheless, further quantification of the technique’s sensitivity and efficiency should be performed along with the application of parallel computation in order to enhance accuracy and decrease computational time of the technique. Yet, the reflectance based IMOPE has presented a high sensitivity for the GNRs presence, being able to detect a very low amount of GNRs within tissues adjacent to the femoral vein while the CT imaging system did not manage to do so.
Acknowledgment
This study was partially supported by European Cooperation in Science and Technology (COST) Action MP1403 “Nanoscale Quantum Optics”.
Disclosure
The authors report no conflicts of interest in this work.
References
Tuchin VV. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis. Vol 13. Bellingham: SPIE Press; 2007. | ||
Ankri R, Duadi H, Motiei M, Fixler D. In-vivo Tumor detection using diffusion reflection measurements of targeted gold nanorods – a quantitative study. J Biophotonics. 2012;5(3):263–273. | ||
Ankri R, Peretz V, Motiei M, Popovtzer R, Fixler D. A new method for cancer detection based on diffusion reflection measurements of targeted gold nanorods. Int J Nanomed. 2012;7:449–455. | ||
Lin AJ, Koike MA, Green KN, et al. Spatial frequency domain imaging of intrinsic optical property contrast in a mouse model of Alzheimer’s disease. Ann Biomed Eng. 2011;39(4):1349–1357. | ||
Yang Y, Celmer EJ, Koutcher JA, Alfano R. UV reflectance spectroscopy probes DNA and protein changes in human breast tissues. J Clin Laser Med Surg. 2001;19(1):35–39. | ||
Jacques SL, Pogue BW. Tutorial on diffuse light transport. J Biomed Opt. 2008;13(4):041302. | ||
Bonner R, Nossal R, Havlin S, Weiss G. Model for photon migration in turbid biological media. J Opt Soc Am A. 1987;4(3):423–432. | ||
Patterson MS, Wilson BC, Wyman DR. The propagation of optical radiation in tissue I. Models of radiation transport and their application. Lasers Med Sci. 1991;6(2):155–168. | ||
Prahl S, Vitkin I, Bruggemann U, Wilson B, Anderson R. Determination of optical properties of turbid media using pulsed photothermal radiometry. Phys Med Biol. 1992;37(6):1203. | ||
Pickering JW, Prahl SA, Van Wieringen N, Beek JF, Sterenborg HJ, Van Gemert MJ. Double-integrating-sphere system for measuring the optical properties of tissue. Appl Opt. 1993;32(4):399–410. | ||
Johns M, Giller C, German D, Liu H. Determination of reduced scattering coefficient of biological tissue from a needle-like probe. Opt Express. 2005;13(13):4828–4842. | ||
Kim A, Wilson BC. Measurement of ex vivo and in vivo tissue optical properties: methods and theories. Optical-Thermal Response of Laser-Irradiated Tissue. 2011:267–319. | ||
Fixler D, Duadi H, Ankri R, Zalevsky Z. Determination of coherence length in biological tissues. Lasers Surg Med. 2011;43(4):339–343. | ||
Lister T, Wright PA, Chappell PH. Optical properties of human skin. J Biomed Opt. 2012;17(9):90901–909011. | ||
Jacques S, Alter C, Prahl SA. Angular dependence of HeNe laser light scattering by human dermis. Lasers Life Sci. 1988;2(4):309–333. | ||
Prahl SA. Light transport in tissue, University of Texas at Austin; 1989. | ||
Graaff R, Dassel A, Koelink M, De Mul F, Aarnoudse J, Zijlstra W. Optical properties of human dermis in vitro and in vivo. Appl Opt. 1993;32(4):435–447. | ||
Chan EK, Sorg B, Protsenko D, O’Neil M, Motamedi M, Welch AJ. Effects of compression on soft tissue optical properties. IEEE J Select Topics Quant Electron. 1996;2(4):943–950. | ||
Simpson CR, Kohl M, Essenpreis M, Cope M. Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique. Phys Med Biol. 1998;43(9):2465–2478. | ||
Meglinski IV, Matcher SJ. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in the visible and near-infrared spectral regions. Physiol Meas. 2002;23(4):741–753. | ||
Salomatina E, Jiang B, Novak J, Yaroslavsky AN. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J Biomed Opt. 2006;11(6):064026. | ||
Zonios G, Dimou A. Modeling diffuse reflectance from semi-infinite turbid media: application to the study of skin optical properties. Opt Express. 2006;14(19):8661–8674. | ||
Bosschaart N, Mentink R, Kok JH, Van Leeuwen TG, Aalders MC. Optical properties of neonatal skin measured in vivo as a function of age and skin pigmentation. J Biomed Opt. 2011;16(9):097003. | ||
Yariv I, Rahamim G, Shliselberg E, et al. Detecting nanoparticles in tissue using an optical iterative technique. Biomed Opt Express. 2014;5(11):3871–3881. | ||
Yariv I, Kapp-Barnea Y, Genzel E, Duadi H, Fixler D. Detecting concentrations of milk components by an iterative optical technique.J Biophotonics. 2015;8(11–12):979–984. | ||
Fixler D, Yariv I. New method to detect organic nanoparticles in live tissue. SPIE Proceedings Vol 9339. 2015. | ||
Gerchberg RW, Saxton WO. A practical algorithm for the determination of phase image and diffraction plane pictures. Optik. 1972;35: 237–246. | ||
Fienup JR. Phase retrieval algorithms: a comparison. Appl Opt. 1982;21(15):2758–2769. | ||
Zalevsky Z, Mendlovic D, Dorsch RG. Gerchberg-Saxton algorithm applied in the fractional Fourier or the Fresnel domain. Opt Lett. 1996;21(12):842–844. | ||
Maier JS, Walker SA, Fantini S, Franceschini MA, Gratton E. Possible correlation between blood glucose concentration and the reduced scattering coefficient of tissues in the near infrared. Opt Lett. 1994;19(24):2062–2064. | ||
Duadi H, Fixler D, Popovtzer R. Dependence of light scattering profile in tissue on blood vessel diameter and distribution: a computer simulation study. J Biomed Opt. 2013;18(11):111408. | ||
Duadi H, Feder I, Fixler D. Linear dependency of full scattering profile isobaric point on tissue diameter. J Biomed Opt. 2014;19(2):026007. | ||
Wang L, Jacques SL, Zheng L. MCML – Monte Carlo modeling of light transport in multi-layered tissues. Comput Methods Programs Biomed. 1995;47(2):131–146. | ||
Welch A, van Gemert MJ, Star WM, Wilson BC. Definitions and overview of tissue optics. Optical-Thermal Response of Laser-Irradiated Tissue. 1995:15–46. | ||
Tuchin VV, Wang L, Zimnyakov DA. Optical Polarization in Biomedical Applications. Springer Science & Business Media; 2006. | ||
Tuchin V. Optical properties of tissues with strong (multiple) scattering. In: Tuchin V, editor. Tissue optics: light scattering methods and instruments for medical diagnosis. Bellingham: SPIE Press; 2007. | ||
Nikoobakht B, El-Sayed MA. Preparation and growth mechanism of gold nanorods (NRs) using seed-mediated growth method. Chem Mater. 2003;15(10):1957–1962. | ||
Fixler D, Ankri R. Subcutaneous gold nanorods [corrected] detection with diffusion reflection measurement. J Biomed Opt. 2013;18(6): 61226. | ||
Shilo M, Reuveni T, Motiei M, Popovtzer R. Nanoparticles as computed tomography contrast agents: current status and future perspectives. Nanomedicine (Lond). 2012;7(2):257–269. | ||
Meir R, Shamalov K, Betzer O, et al. Nanomedicine for cancer immunotherapy: tracking cancer-specific T-cells in vivo with gold nanoparticles and CT imaging. ACS Nano. 2015;9(6):6363–6372. | ||
Motiei M, Dreifuss T, Betzer O, et al. Differentiating between cancer and inflammation: a metabolic-based method for functional computed tomography imaging. ACS Nano. 2016;10(3):3469–3477. |
 © 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.