Back to Journals » Eye and Brain » Volume 6 » Thematic series: Organization and function of the visual system in primates
Mutual information of local field potentials distinguishes area-V2 stripe compartments
Authors Parajuli A, Eriksson A, Felleman D
Received 19 December 2013
Accepted for publication 5 February 2014
Published 24 September 2014 Volume 2014:6(Thematic series: Organization and function of the visual system in primates) Pages 75—95
DOI https://doi.org/10.2147/EB.S51820
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 4
Arun Parajuli, Anastasia Eriksson, Daniel J Felleman
Department of Neurobiology and Anatomy, University of Texas Medical School at Houston, Houston, TX, USA
Purpose: Determining how information is represented by populations of neurons in different cortical areas is critical to our understanding of the brain mechanisms of visual perception. Recently, information-theoretical approaches have been applied to the analysis of spike trains of multiple neurons. However, other neurophysiological signals, such as local field potentials (LFPs), offer a different source of information worthy of investigating in this way. In this study, we investigate how the modular organization of area V2 of macaque monkeys impacts the information represented in LFPs.
Materials and methods: LFPs were recorded from a 32-channel microelectrode array implanted in area V2 of an anesthetized macaque monkey. The electrode positions were recovered in histological tissue stained for cytochrome oxidase (CO) to reveal the modular organization of V2. Visual stimuli consisted of a variety of moving gratings that differed in orientation, direction, spatial frequency, and chromatic content.
Results: LFPs were separated into different frequency bands for analysis of mutual information as a function of stimulus type and CO-stripe location. High-γ-band LFPs revealed the highest information content across the electrode array. The distributions of total mutual information as well as mutual information due to correlations varied greatly by CO stripe. This analysis indicates that local correlations within each CO stripe generally reduce mutual information, whereas correlations between stripes greatly increase mutual information.
Conclusion: The decomposition mutual information based on the power of different frequency bands of LFPs provides new insight into the impact of modular architecture on population coding in area V2. Unlike other cortical areas, such as V1, where mutual information based on LFP correlations is largely determined by cortical separation, mutual information in V2 is also fundamentally determined by the CO-stripe architecture.
Keywords: microelectrode array, cytochrome oxidase, information processing, cortical streams, cortical modules
Introduction
Significant progress has been achieved in our understanding of how visual information is represented within populations of neurons. The vast majority of this insight has come from investigations of single-unit properties in the V11 and medial temporal areas,2,3 where single-unit properties and noise correlations among pairs of neurons have been used to determine both coding efficiency (using Fisher information) and stimulus discriminability (using mutual information [MI]).
Information processing in the visual system has been traditionally investigated based on the spiking activity of populations of cortical neurons.4 More recently, investigators have embraced other biological signals, such as local field potential (LFP), as novel methods of measuring cortical information processing.5–7 Whereas LFPs are generally thought to arise from local postsynaptic potentials, the specific sources that give rise to these signals remain somewhat controversial.8–10 Furthermore, whether and how the variety of frequency bands of LFPs differ in their spatial resolution, cortical extent, and information content remains an issue for continued investigation. This intense interest has also been fueled by the suggestion that LFPs may be highly correlated with the blood oxygen level-dependent signal that forms the basis for most investigations of functional magnetic resonance imaging.5
How information is encoded in the brain has long been debated, especially with regard to whether and how correlations between neurons act to limit or enhance the information encoded by a given population of neurons.4,11,12 Two somewhat complementary approaches have generally been employed to study information processing in the cortex. The first approach focuses on how accurately a population of neurons encodes stimuli. This approach often measures Fisher information using the mean firing rate of neurons and the covariance of neural responses.13 The second approach employs applied Shannon information theory to determine how the activity within a population of neurons provides information about stimuli.14 The resultant MI, measured in bits, “quantifies the reduction of uncertainty about the stimulus that can be gained from observations of a single trial of the neural response”.15,16
Although MI has traditionally been calculated using single-unit firing rates, there has been growing interest in determining the significance and information content of LFPs. LFPs are thought to represent extracellular currents that primarily represent synaptic potentials (eg, excitatory postsynaptic potential) that may be best correlated with synaptic inputs and local processing. In contrast, individual spiking activity is likely correlated with the output properties of a given piece of cortical tissue. Although this formulation suggests that LFP and spiking activity should convey different types of information, recent investigations suggest that some LFP-frequency bands are well correlated with local neuronal spiking.6
LFPs are generally decomposed into four or more frequency bands that largely parallel the frequency ranges traditionally investigated in electroencephalography (EEG) recording with scalp electrodes. The most commonly investigated ranges are 1–13 Hz (δ, θ, α), 13–25 Hz (β1), 25–40 Hz (β2), and 60–120 Hz (γ/high-γ). These different frequency bands are generally thought to differ in their ability to propagate through cortical tissue and to convey different types of information. However, there is a paucity of research comparing LFP-frequency bands to information.
Recently, a powerful toolbox that extends the traditional methods of information analysis to a wider range of neurophysiological signals (including EEG and LFP) has become publicly available.15 One of the important features of this toolbox is the decomposition of total MI (MItotal) into a number of different components that collectively describe the contributions of stimulus tuning and neuronal correlations. Accordingly, Itotal = Ilinear + Isynergy. Ilinear describes the information in a population, represented by either spikes or LFP power, if all elements were completely independent from each other. The Isynergy component comprises the difference between Ilinear and Itotal. This synergy component can take on positive or negative values, depending on whether the interactions between elements increases total information, or whether redundancy between elements results in a reduction in total information. Most importantly for this investigation, Isynergy can be further decomposed into separate terms that reflect the impact of signal (Isig-syn) and noise correlations (Icorrelation).
The influence of noise correlations on population coding is complicated by its dependences on correlation magnitude and signal correlations.12,13 Specifically, high noise correlations between neurons with positive signal correlations tend to reduce information, whereas high noise correlations between neurons with negative signal correlations will increase information. In V1, noise correlations tend to decrease with increased cortical separation between unit pairs.17,18 The high noise correlations observed between unit pairs within a cortical column is thought to be due to a high degree of common input; the reduction in correlations over distance is thought to vary proportionally with the rapid decrease in common input between widely separated cortical columns.10 Although this view is consistent with the known distributions of thalamocortical projections to V1, the relatively homogeneous functional architecture of V1 may not be representative of other cortical areas, many of which contain more pronounced modular architectures distinguished by their functional properties and cortical connections.
Materials and methods
Animal preparation
General animal preparation and experimental procedures were carried out using methods described previously.19–21 All procedures were consistent with the guidelines of the Society for Neuroscience for the use of laboratory animals and approved by the Animal Welfare Committee of University of Texas at Houston Health Science Center. Briefly, one long-tailed macaque monkey (Macaca fascicularis) was prepared for semichronic recording by sterile implantation of a 32-channel microelectrode array into V2. After postoperative recovery, the animal began a series of weekly recording sessions. The animal was anesthetized with ketamine (25 mg/kg) followed by sufentanil citrate (6–12 μg/kg/hour) and paralyzed with pancuronium bromide (0.05 mg/kg/hour) delivered by intravenous infusion (10 mL/kg/hour; lactated Ringer’s 5% dextrose). Electrocardiogram, peripheral capillary oxygen saturation, end-tidal CO2, and temperature were monitored continuously. The eyes were brought into convergence and focused on the screen of a Trinitron monitor by custom-fit contact lenses and a prism. The whole screen (19° × 14°) covered the visual field of the recorded portions of V2 (2°–7° along the vertical meridian).
Recording methods
Single-unit and LFP recording was carried out in a macaque monkey prepared for semichronic electrophysiological recording. Data acquisition was conducted using 32-channel Utah arrays in conjunction with the Cerebus recording system (Blackrock Microsystems, Salt Lake City, UT, USA). Visual stimuli were generated using the Visage system (Cambridge Research Systems, Rochester, UK), which produced luminance and isoluminant chromatic grating stimuli. Orientation and/or chromatic tuning curves were calculated from 10–50 repetitions of each stimulus presented in pseudorandom order.
Visual stimuli
Visual stimuli were generated using the Visage visual stimulation hardware/software environment, and were presented on a Hitachi cathode ray tube monitor. Custom programs enabled the presentation of grating stimuli of variable spatial and temporal frequencies and luminance contrasts. The luminance and chromaticity of the stimulus were calibrated using a J17 LumaColor meter with a J1803 luminance head and a J1820 chromaticity head (Tektronix, Beaverton, OR, USA), and different chromatic gratings were adjusted for equal luminance (within 3%). Visual stimuli consisted of 40 stimuli that differed by chromatic content, orientation, and spatial frequency, which were presented in a pseudorandom order and were repeated 50 times each. All stimuli had average luminance of 14 cd/m2 and were presented on the Hitachi monitor with a background luminance of 14 cd/m2. The first 24 stimuli consisted of luminance-contrast oriented gratings (6 orientations × 2 directions) that were moved perpendicularly to the long axis (2 cycles/second) at two different spatial frequencies (0.5 and 2.0 cycles/degree). The second set of 16 stimuli consisted of moving (2 cycles/second) oriented (4 orientations × 2 directions) isoluminance chromatic (red/gray and green/gray) gratings (0.5 cycles/degree). This rich stimulus set facilitated the identification of color preference-, orientation-, color-, and spatial frequency-specific responses.
Data analysis and interpretation
All analyses of the data were performed using custom software written for MatLab (MathWorks, Natic, MA, USA). The Information Breakdown Toolbox (http://www.ibtb.org)15 was used to compute various MI values.
LFP data filtering and spike sorting
The unfiltered LFP recording was first treated to remove line noise at 60, 120, and 180 Hz. For this, we used a Chebyshev type II filter with 60 db attenuation in the frequency range fn ±0.6 Hz, where fn is the noise frequency to be removed. Then, we filtered the LFP signals into different frequency bands for further analysis. The selected frequency bands and their frequency ranges were: band 1=1–13 Hz, band 2=13–25 Hz, band 3=25–40 Hz, and band 4=60–120 Hz. We used the Chebyshev type II band-pass filter with cutoff frequencies of f1 −0.3 Hz and f2 +0.3 Hz (where f1 and f2 represent the lowest and highest frequencies of the pass band, respectively) and 60 db attenuation in the stop band. To nullify any phase delay introduced by the filter, we filtered and reversed the signal twice (“filtfilt” function on MatLab). After acquisition, spiking data were run through an offline-sorting program (Plexon, Dallas, TX, USA). Spikes were manually sorted into multiunit channels based on several parameters, including principal component analysis, the peak and valley timing and voltage, the shape of the spike, and energy.
Evoked LFP-Power computation
Since ongoing LFP power fluctuates greatly over time, we investigated evoked LFP power due to a stimulus. Evoked LFP power in a specific frequency band was computed using the formula:
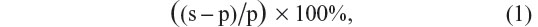
where s and p are the average LFP power values in the specific frequency band during the 500 ms stimulus and 500 ms prestimulus periods of time, respectively. Average LFP power in a time window in a specific frequency band was computed by first filtering the LFP signal in that frequency band and then taking the average of the voltage-squared values within the time window.
Relationships among unit recording, LFP voltage, and LFP power
The relationships among single-unit tuning, LFP wideband and band-limited voltage, and LFP band-limited power are illustrated in Figure 1. In this example, the tuning of an isolated single unit on electrode 28 is illustrated in Figure 1A. This cell was highly selective for orientation, and showed brisk responses to luminance-contrast gratings oriented at 0° and 30°. In contrast, the band–band LFP voltage at this electrode showed robust responses to all orientations, beginning approximately 50 ms after stimulus onset. The band-limited LFP voltages for the four frequency bands used in this study are illustrated in panels C–F. In each of these frequency bands, the LFP voltage demonstrated strong responses to the majority of the tested orientations, but the specific stimulus eliciting the maximal response appeared to vary with the LFP voltage frequency band (eg, 1–13 Hz peak response to stimulus S2; 25–40 Hz peak response to stimulus S5; 60–120 Hz peak response to stimulus S0). In the current analysis, the LFP responses were calculated in a time window of 512 ms after stimulus onset, minus the LFP voltage (or power) occurring 100 ms before stimulus onset. Therefore, despite robust LFP voltage occurring in response to the 60–120 Hz stimulus S5, the largest response in this frequency band occurred with stimulus S0, which is consistent with the single-unit tuning illustrated in panel A.
The band-limited LFP power corresponding to the LFP voltages in panels C–F are illustrated in Figure 1, G–J. In G–J, the LFP power is illustrated as a function of time for each tested orientation. Within each LFP-frequency band and stimulus-specific band, LFP frequency is illustrated vertically such that the lowest frequency within the selected band is located across the bottom of each stimulus-specific segment. These panels demonstrate that LFP band-limited power has a somewhat complex relationship to stimulus orientation, in terms of overall tuning, number of response peaks, and in terms of response latency. For example, the LFP-power responses in the 13–25 Hz frequency band were largely uniform across stimuli, and consisted of two response peaks that occurred at the same latency relative to stimulus onset. In contrast, the LFP-power responses in the high-γ, 60-120 Hz frequency band varied widely in power and latency across tested stimulus orientations. It is notable that the shortest-latency high-γ-band LFP-power responses occurred in response to stimuli S0 and S1, exactly those that elicited the largest single-unit responses.
Noise correlations
Neuronal correlations were measured by computing the trial-by-trial spike-count correlation, known as noise correlation (NC). Before computing NC, the spike data for each stimulus condition were converted to z-scores. The z-scores for all the stimulus conditions were then combined to compute the NC between two electrodes.2
Mutual information
MI in the evoked LFP power in different frequency band was computed using the Information Breakdown Toolbox. MI provides a metric that quantifies the discriminability of a given stimulus based on a single observation of a response, rather than the averaging of responses over many repetitions of the stimulus. The MI approach is particularly appealing, since the methods that have been developed are applicable to different measures of neural activity, including spike counts of single neurons, EEGs, or LFPs. Formally, the information about a stimulus given a response is described by the following:

where Ilinear is the sum of information provided by the responses at each recording site given that each response is completely independent from the other, ie, no signal or noise response variability correlations.
The synergy term reflects the deviation of I(S;R) from Ilinear, and can be either positive or negative. If positive, synergy reflects the synergistic interactions between responses. If negative, synergy reflects redundancy such that different responses across the array carry similar information about the stimulus.
The Icorrelation term quantifies the impact of correlated variability (noise correlations) that are both stimulus-independent (Icorrelation-ind) and stimulus-dependent (Icorrelation-dep). Overall, the impact of Icorrelation-ind on total information depends on the magnitude and sign of signal correlations between responses. Therefore, Icorrelation-ind increases total information when noise and signal correlations have opposite signs, whereas if they have the same sign (eg, both positive signal and noise correlations), total information is reduced, and thus stimuli are less discriminable. We focused our analysis on the total information (MI about stimuli carried by the response array), linear component (the sum of the independent information carried by each element of the response array), and the information due to correlations.
Anatomical methods
At the end of the series of semichronic recording sessions, the monkey was deeply anesthetized with pentobarbital (75–100 mg/kg, intravenously) and briefly perfused intracardially with saline followed by 4% paraformaldehyde in 0.1 M phosphate buffer (pH 7.4). The brain was removed from the skull, and the occipital operculum was dissected, unfolded slightly, gently pressed between glass slides, briefly postfixed in the final cryoprotective solution, and later sectioned in the tangential plane. Frozen sections were cut at 31 μm in thickness.
The pattern of cytochrome oxidase (CO) activity in V2 was demonstrated according to Wong-Riley and Carroll.22 Briefly, free-floating sections were incubated in a large volume of oxygenated reaction mixture for 5–24 hours at 37°C. Sections were then washed, mounted on subbed slides, and air-dried before dehydration and coverslipping. The locations of CO-dense and -pale regions in V2 were digitized using a high-resolution flatbed scanner (1,200 dpi). Radially aligned blood vessels and other fine-edge landmarks were used to align multiple CO-stained histological sections. The locations of all electrodes in the 32-channel microelectrode array were reconstructed relative to the CO pattern observed in the stack of adjacent tissue sections. Optical density analysis was then used to assign each electrode to a CO-dense or -pale region.
LFPs and limited single-unit activity were recorded from electrodes across this array without prior knowledge of their relationship to the pattern of CO stripes. Although the physiological data were strongly indicative of the underlying stripe pattern, the assignment of electrode position to CO stripe was based solely on the histological reconstruction of the array in histological sections stained for CO. Figure 2A illustrates one tangential section through dorsal V2 near the lip of the lunate sulcus that illustrates the 8 × 4 electrode positions with respect to the underlying CO pattern. Although this single section optimally indicates the stripe positions through the two posterior electrode rows, additional sections extended this pattern to the two more anterior rows. Figure 2B illustrates the reconstruction of electrode number (array position) with regard to CO-stripe location. The central CO-dense region was tentatively identified as a CO thin stripe, while the adjacent CO-pale regions were identified as interstripes. These interstripes were further distinguished as type I and type II interstripes, based on their positions medial and lateral to the thin stripe, respectively. The functional assignment of CO-dense and -pale regions was based on the consistent physiological23 and anatomical criteria24 that indicate that type II interstripes are located medial to each thick stripe.
Results
Area V2 is a well-studied extrastriate cortical area with a distinct modular architecture that is characterized by a unique pattern of CO-defined stripe compartments, distinct functional properties, and distinct cortical connections. V2 therefore provides an excellent opportunity to determine how the characteristic modular architecture influences the coding of MI by LFPs. In this study, LFP and limited single-unit recording was performed using a 32-channel silicone microelectrode array. The array position was subsequently recovered in a stack of histological sections stained for the metabolic enzyme CO. To facilitate the identification of functional differences between electrodes and thus V2 stripes, a rich set of visual stimuli were presented that differed in chromatic content and spatial frequency. This section presents data that examine the distribution of the linear component of MI (MIlinear) across LFP-frequency bands, the breakdown of total MI (MItotal) into its key components, and the systematic analysis of MI due to correlations (MIcorrelation) between V2 stripes. The pattern of MI varied systematically across the microelectrode array. These systematic variations provided new insights into the pattern of interstripe correlations and functional properties of V2 stripe compartments.
Mutual information and LFP-frequency bands
The pattern and magnitude of MIlinear encoded by LFPs varied by frequency band and visual stimulus content. This basic result is illustrated in Figure 3, which displays the MIlinear encoded by each of the 32 microelectrode-array channels in the two stimulus epochs (and total stimulus set; columns) and four LFP-frequency bands (rows). The MI in each LFP band in each frequency and stimulus condition is color-coded such that higher information values are indicated by shades of red and lower information values are indicated by shades of blue. The pattern of electrodes displaying high LFP MI changes both with LFP frequency and stimulus epoch. Within the luminance-contrast stimulus set (stimuli 1–24), the lowest-frequency band displayed little evidence of high LFP MIlinear, which clearly increased across the array for the middle frequency (13–25 and 25–40 Hz) bands. Most interestingly, in the high-γ-frequency band, the highest LFP information was observed in the lateral and medial portions of the microelectrode array, corresponding to the interstripe regions.
A distinctly different pattern of LFP MI versus LFP-frequency band was observed within the second (chromatic) stimulus epoch. In contrast to the first stimulus epoch, LFP MIlinear at the lowest frequency band showed weak evidence for increased information in the middle electrode channels. A very similar pattern was observed within the 13–25 Hz band, in which MI grew even stronger within the 25–40 Hz band. In contrast to the first stimulus epoch, the electrodes with highest γ-band (60–120 Hz) LFP information were concentrated in the central portion of the array, corresponding to the CO thin stripe.
Mutual information within the high-γ-frequency band
Strong evidence for distinguishing different CO stripes on the basis of the MIlinear encoded within LFP power was first revealed by comparing the pattern of MIlinear across the electrode array under different stimulus conditions (Figure 4). The central electrodes appeared to be contained within a thin stripe, based on the data revealed by the differential MI map in Figure 4A. This map illustrates the numerical difference in MI bits when the information contained within responses to the chromatic stimulus set (stimuli 25–40) is subtracted from the information contained within the responses to the luminance-contrast stimulus set (stimuli 1–24). The largest negative values (chromatic > luminance) were found within columns 3–4, which correspond to the CO-dense region illustrated in Figure 2. Based on this analysis, it is concluded that this central CO dense region is a thin stripe.
The map of MIlinear revealed by the responses to the chromatic stimulus set was further examined by comparing the magnitude of MI found in the brain responses to the red/gray – green/gray-oriented chromatic stimulus conditions (stimuli 25–32 minus 33–40), as illustrated in Figure 4B. Similar to the spatial pattern of MIlinear exhibited in Figure 4A, the differential information plot in Figure 3B highlights a central zone (columns 4–5) that contains a relatively high information content, reflecting the processing of different hues in the chromatic stimulus set. Most interestingly, this high-information “stripe” does not directly superimpose on the high-information stripe in Figure 4A. Perhaps this slight offset (~400 μm) indicates a spatial substructure within the thin stripes.19 In addition, the spatial pattern of MIlinear in Figure 4B indicates an asymmetry in the information content in the two interstripes that flank the central thin stripe. Specifically, the interstripe located medially to the thin stripe (type I interstripe) exhibited greater information values within the responses to the red/gray stimulus, while the interstripe lateral to the thin stripe (type II interstripe) exhibited greater information in responses to the green/gray stimuli. A similar asymmetry was observed within the differential MI plot in Figure 4A: the medial interstripe exhibited greater information about the luminance stimulus set, whereas the lateral interstripe contained more information about the chromatic stimulus set.
A complementary pattern of differential MIlinear is revealed in Figure 4C, which compares the MI contained within the responses to low- versus high- spatial frequencies (stimuli 1–12 versus 13–24). In this comparison plot, the central thin stripe exhibited relatively low information about these luminance-contrast stimuli, whereas the medial and lateral interstripes exhibited relatively large and asymmetrical information about these stimuli. Specifically, the medial (type I interstripe) exhibited greater information about the higher-spatial-frequency stimuli, whereas the lateral interstripe (type II interstripe) exhibited greater information about the lower-frequency stimuli. These results demonstrate that the MI contained within the responses to stimuli varying in chromatic content and spatial frequency can provide robust evidence to distinguish thin stripes from interstripes. Furthermore, this analysis suggests that the two types of interstripes can be distinguished by the MIlinear contained in their responses to luminance and chromatic stimuli.
Noise correlations are fundamental to population coding of mutual information
Total MI within a neural population is composed of several distinct components, reflecting both the linear, independent information due to the responses of individual neurons (or LFP sources) and the synergistic effects of interactions between neural elements. Information is either increased or decreased, based primarily on the correlations between neural responses. It is now recognized that the presence of correlations between neural elements does not automatically reduce MI because of redundancy, Rather, the determination of whether a correlation adds or subtracts information depends in a complex way on the sign of both the noise and signal correlations between elements. That is, if two cells (or LFPs) have similar stimulus-tuning properties, a positive noise correlation between them will tend to reduce MI, while a negative noise correlation will tend to add MI. Conversely, if two neural elements have dissimilar tuning properties, both positive and negative correlations can increase MI. Since correlated variability (noise correlations) can have such a critical role in population coding of MI, it is important to determine the spatial structure and stimulus dependence of noise correlations in V2.
In the current experiment, several recording sessions were particularly useful in providing single-unit data from multiple electrode channels that facilitated the determination of the magnitude, spatial dependence, and stimulus specificity of noise correlations. These data were analyzed separately for the two types of stimulus sets: oriented luminance and nonoriented, isoluminant hue stimuli. In contrast to LFP recording, on several occasions it was possible to isolate two or more single units from a given electrode, and thus calculate their noise correlation with 0 mm unit separation. The pattern of noise correlations for 53 pairs of single units recorded during stimulation with moving oriented luminance-contrast gratings is illustrated in Figure 5A. In order to gain some insight into the relationship between these noise correlations and the corresponding signal correlations, the unit pairs were distinguished by the differences in their preferred orientations, and in the case of differences greater than 60°, by their stripe-to-stripe positions. The noise correlations for unit pairs whose preferred orientations differed by 60° or less were moderately high for closely separated pairs, and the magnitude of this correlation decreased rapidly with increasing cortical separation (y =−0.0642x+0.2205). In contrast, the unit pairs whose preferred orientations differed by more than 60° exhibited noise correlations that were impacted by their CO-stripe position in the cortex. For example, the noise correlations from the subset of these unit pairs that spanned between the two interstripes were remarkably high given their large cortical separation of ~2 mm (y=−0.2176x+0.6622). On average, unit pairs with orientation differences of 60° or less that were separated by 1.5–2.5 mm had noise correlations that averaged near 0.1. Finally, the small group of unit pairs with orientation differences greater than 60° showed very low noise correlations at separations of ~1 mm, and exhibited somewhat-larger noise correlations at separations near 1.75 mm (y=0.1091x−0.0442). Although this latter group is described as not spanning between interstripes, their large cortical separations and higher noise correlations suggest that they may have encroached on these interstripes.
The pattern of noise correlations calculated for 81 unit pairs during isoluminant hue stimulation is illustrated in Figure 5B. As with the pattern of noise correlations observed during stimulation with oriented luminance-contrast gratings (Figure 5A), hue-driven noise correlations were maximal for unit pairs recorded at the same microelectrode (unit separation =0), and decreased to an average of less than 0.1 for unit-pair separations of ~2.5 mm (y=−0.0821x+0.2548). Although this analysis did not evaluate the specific stripe identities of the units in these pairs, the cortical separations of >1.5 mm almost certainly included some units spanning between the two interstripes.
These patterns of noise correlations as a function of unit-pair cortical separation are consistent with the prevailing view that high noise correlations reflect substantial common input.1,13 This would be expected for closely separated unit pairs, as the amount of shared input would be expected to decrease with increasing cortical separation. However, the high noise correlations observed for unit pairs that spanned across interstripes would not be expected by a simple homogeneous-distance model that has been applied to V1.1 Rather, these high noise correlations would be consistent with the idea that despite their large cortical separations, the two interstripes of V2 receive a substantial amount of common input. Although these two types of interstripes receive the majority of their input from layers 2 and 3 of V1, a vanishingly small percentage of individual cells project to two different interstripe types.24
Mutual information changes with reference to electrode position
As indicated earlier, the MItotal contained within the responses of a given neural population depends both on a linear component resulting from independent signal correlations and a nonlinear component reflecting the positive and/or negative impact of interneuronal correlations. In order to gain some insight into the distribution and impact of LFP correlations, a strategy was developed to sample the structure of correlations across the microelectrode array using a single reference electrode whose effective position was systematically shifted across the array. This strategy can be seen in Figure 6, which plots the MItotal encoded within the responses in the two stimulus subsets and the total stimulus set for high-γ-frequency LFPs. Each row of this figure illustrates the pattern of MItotal across the array for a single reference-electrode position. The specification of the reference electrode allows for the calculation of LFP correlations with all other electrodes in the array. As before, the MI calculated for each electrode is color coded; reds are high information and blues are lower information.
While each of the stimulus epochs and the total stimulus set conveyed similar information about the impact of LFP correlations on MItotal, the second stimulus epoch (stimuli 25–40) may be the most illustrative. In the e2 reference condition, the highest MItotal was observed in the central region corresponding to the thin stripe (columns 3–5), and in the most lateral columns corresponding to the type II interstripe at the thick-stripe border. In contrast, the lowest MItotal was observed in the most medial columns in the immediate vicinity of the reference electrode. This pattern suggests that correlations near the reference site reduce the MItotal arising from that region. A similar pattern of high centrally located MItotal and low medial interstripe information was observed in the e6 reference-electrode condition. This pattern of reduced MItotal in the vicinity of the reference electrode is consistent with the idea that LFP correlations within a given CO-stripe compartment act to reduce the MItotal represented within that stripe.
The suggestion that stripe-specific correlations reduce the MItotal exhibited by a given CO stripe is further supported by the pattern of information observed in reference-electrode conditions e10–e14, and to a somewhat lesser extent in e18. For example, in the case of reference electrode e10 (center of column 3), the highest MItotal was exhibited by LFPs recorded at the medial and lateral extremes of the array, while the lowest MItotal was exhibited by electrodes in the immediate vicinity of the reference electrode (located within the central thin stripe). A very similar pattern of MItotal was observed in reference electrode condition e18. This shifting distribution of MItotal is very striking, and raises a number of issues concerning the distribution of LFP (and single-unit) correlations in V2. If the inclusion of a reference electrode allows for the incorporation of local neural correlations, the region of reduced local information, presumably due to increased local correlation, is not simply one electrode wide. Rather, the observed increases or decreases in MItotal appear to shift with a period of approximately three electrode separations (~1.2 mm). Therefore, the most parsimonious explanation of this result is that the reduction in MItotal is most likely due to increased correlations (LFP noise correlation) reflecting the spatial spread of common input to each V2-stripe compartment.
This idea is further supported by the shift in MItotal observed with reference-electrode positions e22 and e26. These two reference conditions exhibited a pattern of MItotal very similar to that exhibited with reference electrodes e2 and e6. The similarity of array-wide MItotal in the face of widely disparate reference-electrode positions suggests that the distribution and impact of correlations arising from the two interstripes was largely symmetrical. Finally, reference-electrode condition e30 presented a pattern of MItotal that was somewhat difficult to interpret. In this condition, high MItotal was exhibited across the whole array with little or no evidence of reduced information due to local correlations. Perhaps electrode e30 fell just outside the lateral (type II) interstripe, and thus is best interpreted as falling at the edge of the thick stripe. If so, then one interpretation of the observed result is that thick stripes do not follow the same correlation/MI rules that seem to be reflected in the thin stripes and interstripes. Alternatively, the distribution of local intrinsic connectivity and associated neural correlations are robust within a given stripe cycle and less extensive between stripe cycles. According to this view, the thick stripe, located at the extreme lateral edge of the electrode array, might be part of the next stripe cycle, while the thick stripe that should be located at the extreme medial edge of the array would be part of the current stripe cycle. A formal test of the stripe-cycle dependence of neuronal correlations will require considerable additional experimentation to measure correlations and information across two or more stripe cycles.
The incorporation of pair-wise correlations associated with the reference electrode had a profound impact on the magnitude and structure of MItotal across the microelectrode array. For each reference-electrode position, the associated correlations increased the MItotal in a way that depended on stripe position. In an effort to gain further insight into the significance of these findings, we decomposed the MItotal into its linear and correlational components, and examined how these information sources changed as a function of reference-electrode position across the array. Figure 7A illustrates in a compact format the impact on MItotal that was represented in Figure 6. Similar to Figure 6, the information associated with the luminance (stimuli 1–24), chromatic (stimuli 25–40), and total (stimuli 1–40) stimulus sets are plotted separately. Within each of these plots, the reference-electrode position varies along the x-axis, and the information magnitude (bits) is plotted along the y-axis. Unlike Figure 6, this figure averages the information values for all electrodes within a given stripe type: red for the lateral interstripe, green for the central thin stripe, and purple for the medial interstripe. Finally, dashed vertical lines in the panels representing the chromatic stimulus epochs indicate the position of the thin stripe relative to the plotted MI-component values.
The overall impact of the inclusion of the reference electrode on MItotal is best evaluated by examining how the MIcorrelation (Figure 7C) when added to the MIlinear due to independent responses (Figure 7B) resulted in the pattern of MItotal represented in Figure 7A. For example, the MIlinear encoded within the responses to the luminance stimulus set (stimuli 1–24) was relatively flat across the microelectrode array, and averaged approximately 1.1 bits/electrode. In contrast, the MI encoded by interelectrode correlations (MIcorrelation) was generally smaller in magnitude, but varied considerably with reference-electrode position and stripe type. In this example, the MIcorrelation varied from 0 to 0.7 bits and was highly dependent on stripe type. That is, MIcorrelation in the thin stripe was high when the reference electrode was located in either interstripe, but was nearly zero when the reference electrode was located within the thin stripe. Similar but less profound effects were observed in the lateral and medial interstripes.
A similar but more complex pattern of MI components was observed in the responses to the chromatic stimulus set (stimuli 25–40). In general, the magnitude and pattern of MItotal from the chromatic stimulus epoch was very similar to that observed in the luminance-stimulus epoch. These stimulus epochs differed greatly in the magnitude and distribution of the MIlinear component, as well as in the detailed structure of the MIcorrelation. For example, unlike the relatively flat distribution of MIlinear for the luminance stimuli, this information component was generally greater in magnitude and varied in reference to electrode position in the responses to the chromatic stimulus set. It is striking that MIlinear peaked at the borders of the thin stripe and in fact dipped within the center of this stripe. Furthermore, it is interesting that all three stripe components had additional minima at reference-electrode positions 2 and 26. Based on the previous analysis, it appears that e2 was located within the interstripe near the next thick stripe, whereas e26 may have been located at the far lateral edge of the interstripe, with e30 located just inside the next thick stripe.
MIcorrelation encoded within the responses to the chromatic stimulus set also varied greatly with stripe type and reference-electrode position. In some ways, this distribution was similar to that seen in the responses to the luminance-stimulus set, but there were also some differences that may provide insight into the functional interactions between V2-stripe types. Unlike the luminance set responses, the MIcorrelation within the two interstripes peaked for the reference-electrode position in the center of the thin stripe (e14) and was slightly asymmetrical with respect to the thin stripe. Specifically, the MIcorrelation within the medial (type I) interstripe was lowest for reference position e6 and was relatively high for reference-electrode positions within the lateral interstripe (e22–e30). A largely complementary pattern of MIcorrelation was observed in the lateral interstripe (type II). In this case, the largest information was observed for correlations arising from the medial interstripe region (e2–e6), and the smallest information was observed for correlations arising from within the lateral interstripe (e22–e24). Finally, the MIcorrelation observed within the thin stripe was near zero or slightly negative within the thin stripe, and increased rapidly to peak values for correlations arising from the centers of the medial (e2) and lateral (e26) interstripes.
The spatial distribution and stripe dependence of the MIcorrelation of LFPs is striking, and raises a number of issues concerning interactions between V2-stripe compartments. First, for each stripe type, the correlations that arose locally generally provided little or slightly negative amounts of MI. This effect was most profound within the thin stripe and medial interstripe. However, the local correlations arising within the lateral interstripe, at least during chromatic stimulation, had a generally positive impact on MI. Second, for all stripe types, the correlations arising from more distant electrodes tended to have strongly positive impacts on MItotal. Finally, the MIcorrelation curves varied in shape for the different V2 stripes. Specifically, the MIcorrelation curve within the thin stripe was very broad, and peaked at distances of approximately 1.2 mm. In contrast, the MIcorrelation curve for the medial interstripe (type I) exhibited a very narrow minimum (around one electrode), and the peak information was observed approximately 800 μm away. Similarly, the curve for the lateral interstripe (type II) contained only a modest, narrow dip and near-peak values of MI were observed ~800 μm away. These asymmetries imply that the spatial extent of local, intrinsic connections differed by stripe type. According to this hypothesis, thin stripes make more widespread connections than either type of interstripes. Furthermore, if the distribution of MIcorrelation in LFPs is related to single-unit noise correlations, these results are consistent with the idea that the border regions of CO stripes contain a mixture of cells that collectively exhibit more common input than those in the centers of each stripe.
Mutual information changes due to specific interstripe interactions
Having established that the pattern of MItotal was systematically influenced by the horizontal position of the reference electrode relative to the CO stripes, we then expanded this analysis by determining the full impact of interstripe correlations on MI. The results from this analysis are presented in Figure 8, which illustrates how MI in each stripe compartment was impacted when the correlations from each of the three stripes were included as the “reference”. This figure is organized by columns into the achromatic, chromatic, and full-stimulus sets. The first three rows illustrate the impact of these stripe–stripe interactions on the high-γ-band (60–120 Hz), MItotal, MIlinear, and MIcorrelation, respectively. The bottom row illustrates the impact of these stripe–stripe interactions on 1–13Hz MIcorrelation. Furthermore, the bar graphs in the first two rows are scaled to the same maximum value (two bits of MI) to highlight the differences between MItotal and MIlinear, and thus to facilitate appreciation of the role of MIcorrelation in MItotal.
Within each bar-graph plot, three sets of bar graphs are shown that illustrate the impact on MI when all electrodes within each CO-stripe type are used as “reference” (type II interstripe, thin stripe, type I interstripe, respectively). The three bars within each of these three graph sets therefore illustrate the amount of MI (mean ± standard error of mean) encoded within each of these stripe types. For example, the upper-left panel demonstrates for the achromatic stimulus set (stimuli 1–24) how high-γ-band MItotal in each CO stripe is influenced by the correlations arising from each stripe. These plots reveal several different aspects of MItotal within each stripe as a function of stripe-to-stripe interactions. First, the comparison of MItotal for each stripe under the three reference conditions demonstrates that MItotal within a given stripe was minimized when the electrodes within that stripe were used for the reference condition. That is, the MItotal within the interstripe II (inter-II), thin, and interstripe I (inter-I) were minimized for the “inter-II”, thin, and “inter-I” reference conditions, respectively. Second, the differences in MItotal revealed across stripe types in each reference condition were statistically significant (Kruskall–Wallis; P<1.88 × 10−11, 1.00 × 10−18, and 3.66 × 10−7). Having established that MItotal varied significantly across stripe type in each reference condition, pair-wise comparisons (uncorrected) were used to determine stripe–stripe differences in MItotal. Therefore, for the type II interstripe reference condition, MItotal was found to be significantly different between the type II interstripes and the thin stripes (Wilcoxon, P<1.39 × 10−9), the type II and type I interstripes (P<1.00 × 10−18), and between the type I interstripe and the thin stripe (P<0.047).
The impact of interstripe interactions on MI was most clearly revealed by analyzing the impact of specific stripe interactions on MIcorrelation. The three panels within the third row in Figure 8 illustrate these stripe-specific interactions for the achromatic, chromatic, and full stimulus sets, respectively. As before, the MI within each stripe is illustrated for each of the three stripe-type reference conditions. Similar to the distributions of MItotal for the achromatic stimulus conditions (eg, stimuli 1–24), MIcorrelation varied significantly between stripes in each reference-stripe condition (P<1.99 × 10−8, P<1.00 × 10−18, and 1.55 × 10−9 for reference inter-II, thin, and inter-I, respectively). Furthermore, the plots of MIcorrelation in the achromatic, chromatic, and full stimulus set conditions clearly demonstrate that local, within-stripe interactions tended to reduce MIcorrelation within each stripe. For example, within the achromatic stimulus set, the MIcorrelation for each stripe was lowest in the corresponding reference-stripe condition. This is most noticeable within the achromatic and chromatic stimulus sets, where the MIcorrelation was negative for the thin stripe in the thin-stripe reference condition. Finally, whereas MI (total, linear, and correlation) was found to vary significantly across stripes in each reference-stripe condition in each stimulus set, and individual stripes tended to vary significantly from each other in these conditions, a minority of stripe–stripe comparisons were found to be statistically nonsignificant in this data set. For example, the MIcorrelation for thin versus inter-I in the interstripe II reference condition (P>0.776), inter-I versus inter-II in the thin-stripe reference condition (P>0.481), and inter-II versus thin in the interstripe I reference condition (P>0.174) were each found to be nonsignificant.
In an effort to determine whether the pattern of stripe–stripe interactions observed for high-γ-band MI was unique to this frequency band, we repeated the analysis of MIcorrelation for the LFP power recorded within the 1–13 Hz spectrum (Figure 8D). Overall, the pattern of 1–13 Hz MIcorrelation as a function of CO stripe, reference stripe, and stimulus period was very similar to that observed within the high-γ (60–120 Hz)-frequency band. However, several differences in MIcorrelation are worth pointing out. First, the average MIcorrelation within the 1–13 Hz band tended to be smaller than the high-γ-band MIcorrelation for the same stripes, reference stripes, and stimulus periods. Although not quantified here, this trend was most obvious in the plots of MIcorrelation for the full stimulus set where the high-γ MIcorrelation values tended to exceed those of the 1–13 Hz band by approximately 0.1 bit. Second, whereas a few stripe–stripe interactions in the high-γ-band resulted in negative MIcorrelation (eg, thin stripe in thin-stripe achromatic reference condition), the frequency and magnitude of these negative MIcorrelation values were increased within the 1–13 Hz LFP-frequency band.
Mutual information due to all interstripe interactions
In the previous section, the impact on MI was determined separately for stripes based on interactions from each of the three reference-stripe positions. Although this provides for a comprehensive analysis of specific interaction, it is somewhat artificial, in that interactions between all stripe compartments are expected to occur simultaneously during natural stimulation. Therefore, these data were reanalyzed in order to represent the global pattern of MI based on all of the aforementioned stripe-to-stripe interactions.
The stripe-specific distributions of high-γ-frequency MItotal, MIlinear, and MIcorrelation for the achromatic, chromatic, and full stimulus sets (columns) are illustrated in Figure 9A–C, respectively. Similar to Figure 8, the stripe-specific distributions of MI arising from the 1–13 Hz frequency-band LFP power are illustrated in D. In contrast to Figure 8, the value of MI depicted by each bar in this set of graphs reflects the information contained within the responses of the LFPs spanning all electrodes attributed to each CO-stripe compartment. Like Figure 8, the bar graphs for MItotal and MIlinear are scaled equally to facilitate their comparisons.
This figure summarizes a number of important features about how MI is encoded by each stripe type under different stimulus conditions. 1) MItotal, MIlinear, and MIcorrelation varied significantly across these three CO compartments in the achromatic, chromatic, and full stimulus data sets (Kruskal–Wallis). 2) Pair-wise comparisons of these MI components across stripes and stimulus conditions revealed that stripe-pair comparisons were statistically significant in all stimulus conditions (eg, MItotal for inter-II versus thin), whereas other stripe-pair comparisons were nonsignificant in some stimulus conditions (eg, MIlinear for chromatic inter-II versus inter-I, P>0.298; MIcorrelation for achromatic inter-II versus inter-I, P>0.210; MIcorrelation for chromatic inter-II versus inter-I, P>0.375). 3) MIlinear was greater in the thin stripe than in the interstripe II or interstripe I for both the achromatic (P<1.00 × 10−18, P<4.64 × 10−4) and chromatic (P<1.00 × 10−18, P<1.00 × 10−18) stimulus sets, but not for the full 40-stimulus data set. 4) The MIcorrelation in the type II interstripe was greater than the thin stripe in the achromatic stimulus set (P<6.36 × 10−7; P<1.41 × 10−7), chromatic set (P<4.28 × 10−7), and full-stimulus set (P<7.99 × 10−4). The MIcorrelation in the type I interstripe was greater than the thin stripe in the achromatic stimulus set (P<1.41 × 10−7) and in the full stimulus set (P<0.031), but not in the chromatic stimulus set (P>0.375).
The stripe-dependent distribution of MIcorrelation derived from LFP power in the 1–13 Hz frequency band (D) also distinguished between CO-stripe compartments, but differed from the high-γ MIcorrelation in several ways. Similar to the high-γ-band MIcorrelation, MIcorrelation in the 1–13 Hz band varied significantly across stripes in the achromatic (P<1.00 × 10−18), chromatic (P<5.28 × 10−9), and full-stimulus (P<0.003) sets. However, comparisons of 1–13 Hz MIcorrelation across stimulus epochs and stripes revealed several differences in MI magnitude. Whereas 60–120 Hz MIcorrelation within the type II interstripe was indistinguishable from that of the type I interstripe in the achromatic and full-stimulus sets, 1–13 Hz MIcorrelation in the type II interstripe was significantly greater than in the type I interstripe in all stimulus epochs (P<1.00 × 10−18, P<60.4 × 10−10, and 7.77 × 10−4 for the achromatic, chromatic and full stimulus sets, respectively). Conversely, whereas the 60–120 Hz MIcorrelation in the type I interstripe was significantly greater than in the thin stripe in both the achromatic (P<1.41 × 10−7) and full-stimulus (P<0.031) sets, the 1–13 Hz MIcorrelation of the type I interstripe was indistinguishable from the thin stripe in the achromatic (P>0.300) and chromatic (P>0.271) stimulus epochs, and was marginally distinguishable within the full stimulus set (P<0.030). Although the physiological bases for these LFP-frequency band-specific impacts on MI remain unclear, these results demonstrate that interstripe interactions reflected by MI differ by LFP frequency.
The reproducibility of these results was explored by comparing the calculated values of 60–120 Hz MItotal, MIlinear, and MIcorrelation associated with each of the three CO stripes across three different recording epochs. The comparison of the MI results between sessions 1 and 2 is illustrated in Figure 9E. The correlation between these stripe-specific MI values was robust (R2=0.961) and highly statistically significant (P<4.44 × 10−19). A strikingly similar result was observed when comparing sessions 2 and 3 (not illustrated; R2=0.965 and P<1.08 × 10−19). Therefore, we conclude that MI due to high-γ LFP power across this array is rather stable, and can be used to explore the functional significance of V2-stripe compartments.
Discussion
We recorded LFPs through a 32-channel microelectrode array positioned in area V2 to determine how populations of neurons in a cortical area characterized by a distinct modular organization encode information about sensory stimuli. The investigation of population coding of MI in an area dominated by anatomically defined cortical modules is unique, and the results demonstrate that modular architecture has a profound impact on the structure of neuronal correlations, and thus on how stimuli are represented in the brain. In this section, we discuss how the analysis of MI derived from the power of LFPs provides new insight into the functional architecture of area V2.
LFP linear mutual information in V2 reveals CO-stripe structure
The experimental design of the current experiment enabled the analysis of LFP MI across a variety of stimulus conditions that were chosen to highlight the differences in response properties of neurons across V2 CO stripes. A total of 40 different moving grating stimuli were presented that differed in orientation, direction of movement, spatial frequency, and chromatic/luminance contrast. The first piece of evidence that MIlinear could provide some insight into the functional architecture of V2 came from examining the magnitude of MI (bits) from stimulation with luminance-contrast gratings and isoluminant chromatic gratings. As expected from previous single-unit studies of tuning properties across V2 stripes25–27 and intrinsic imaging studies,19,28 the central thin stripe exhibited substantial MIlinear during chromatic stimulation compared to luminance-contrast stimulation (see Figure 3). Although the basic pattern of thin-stripe predominance was observed across the different LFP-frequency bands, the greatest MIlinear was observed in the high-γ-frequency band (60–120 Hz). A similar distribution of MIlinear was also observed in the responses to the luminance-contrast stimulus set. In this stimulus epoch (stimuli 1–24), little MIlinear was observed in the 1–13 Hz LFP power band, but thin-stripe predominance was still observed for the MI in frequency bands 13–25, 25–40, and 60–120 Hz.
Comparisons of MIlinear in the responses to different subsets of stimuli also provided evidence for the modular organization of V2. In comparing MIlinear of high-γ-band LFP power during luminance-contrast minus chromatic contrast stimulation (Figure 4A), the thin stripe exhibited more information about the chromatic stimulus set, whereas the medial interstripe (type I interstripe) exhibited more information about the luminance-contrast stimuli. These patterns of MIlinear were explored further by examining the pattern of MI within the two different stimulus epochs. The comparison of MIlinear in the responses to red/gray and green/gray stimuli revealed an intriguing pattern of results (Figure 4B). Although the peak responses were observed in central portions of the array, they were not entirely aligned with the luminance-chromatic information described earlier. Instead they were slightly shifted laterally, perhaps indicating the spatial segregation of iso-hue responses that characterize V2 thin stripes. Furthermore, the asymmetrical distribution of MIlinear in the adjoining interstripes is very curious, and implies a preferential representation of red/gray stimuli in the type II interstripe.
Finally, additional evidence for CO-stripe differences was revealed in the differential distribution of MIlinear in the responses to different spatial frequencies within the luminance-contrast stimulus set (Figure 4C). These data indicate that the responses within the type II interstripe (lateral) exhibited greater information about high spatial frequencies, whereas the responses within the type I interstripe (medial) exhibited greater information about low spatial frequencies. The significance of this observation is difficult to assess, since little or no information exists concerning spatial frequency tuning in different V2 interstripes.
Mutual information due to correlations reveals structure of interstripe interactions
The MItotal exhibited by the high-γ LFP-power responses was greatly impacted by the pattern of correlations across the microelectrode array. Comparisons between MIlinear and MItotal (eg, Figure 6A and B) indicate substantial increases in information due to these neuronal interactions. However, the pattern of increased information due to specific correlations was not uniform and appeared to reflect CO-stripe borders and functional specialization. In more homogeneous areas, such as V1, the single-unit noise correlations are expected to decrease rapidly with cortical separation. If the tuning properties of these neurons were largely uniform, then MItotal should also decrease smoothly with cortical separation. In contrast, the current results suggest that the magnitude of correlations across V2 is highly dependent upon CO stripe, and not simply a function of cortical separation.
The impact of CO-stripe structure of MItotal is very striking in that local correlations (in the vicinity of the reference electrode) act to reduce local information while simultaneously increasing information at sites up to 2.5 mm away. Most importantly, the region of reduced information appears to “occupy” the full stripe or interstripe width, rather than be limited to a specific ~200 μm radius. This stripe-specific reduction of MI was further revealed by the near-uniformity of the pattern of information, despite two to three successive shifts in the reference-electrode position (see Figure 6B). These patterns of results suggest that the local correlations within each stripe compartment acted to reduce MItotal, perhaps due to similarities in tuning properties (signal correlations), whereas more distant correlations between stripe compartments acted to increase MItotal, perhaps due to their differing signal correlations.
This idea is further supported by the more complete and quantitative analysis of stripe-to-stripe interactions depicted in Figure 8 and in the quantitative summary of interstripe interactions depicted in Figure 9. These complete stripe analyses clearly demonstrate that local correlations originating within each stripe acted to reduce the contribution of MIcorrelation to MItotal within each stripe type. These analyses also demonstrate that the impacts on MI observed using the single reference electrode approach can be generalized to the entire stripe. Therefore, the impact of intra- and interstripe interactions depicted in Figures 8 and 9 more closely replicates the physiological interactions that are expected to occur in response to extended stimuli during natural vision.
Mutual information in different LFP-frequency bands
The general similarities in the distribution of MIlinear and MIcorrelation across LFP-frequency bands was somewhat unexpected. The prevailing view is that the various frequency bands of LFPs differ in their ability to propagate across the cortex17 and in the information they convey.6,10 Numerous studies suggest that the γ-(or high-γ)-frequency LFP band propagates the least across the cortex and conveys information very similarly to a single-unit firing rate.6,10 In contrast, the lowest LFP-frequency band (1–13 Hz) is thought to propagate over considerable cortical distances and to convey information that is distinct from the γ-LFPs.6,10,17 Furthermore, a recent study suggests that LFP bands between these two extremes convey little or no information about visual stimuli when presented as natural scenes in a movie loop.10 It is difficult to reconcile these ideas with the results from the current study.
Although the lower-frequency LFP bands were expected to have the least spatial resolution, the distribution of MIlinear (Figure 3A) was most restricted for the 1–13 Hz band in each of the luminance, chromatic, and full-stimulus epochs. For each of the higher-LFP-frequency bands, a somewhat similar pattern of higher-information electrodes emerges. Since many factors contribute to the pattern of MIlinear, it is difficult to determine whether the increased “spread” of MIlinear was due to an “iceberg effect” or whether the increases in MIlinear were due to the greater spatial resolution of higher-frequency LFPs. The resolution to this issue will require careful analysis of unit signal and noise correlations and their subsequent comparisons with LFP MI components across frequency bands and CO stripes.
Conclusion
LFP and limited single-unit recording was performed through a 32-channel microelectrode array that was implanted into the V2 area of a macaque monkey prepared for semichronic, anesthetized recording. Subsequent to the recording sessions, the position of each electrode in the microelectrode array was reconstructed relative to the pattern of CO stripes observed in a stack of tangential histological sections. MItotal and its components were calculated using the Information Breakdown Toolbox15and their cortical distributions were analyzed with respect to stimulus type and LFP-frequency band. The spatial distribution of MIcorrelation was perhaps the most informative in that increases and decreases in MI were clearly associated with the positions of CO-stripe borders. In addition, the asymmetrical distribution of MI associated with the two interstripes flanking the central thin stripe provides additional support for the functional distinction of type I and type II interstripes.
Author contributions
All authors made substantial contributions to conception and design, acquisition of data, or analysis and interpretation of data. All authors took part in drafting the article or revising it critically for important intellectual content. All authors gave approval to the final version to be published.
Acknowledgments
The authors thank Valentin Dragoi and the various members of his laboratory for their helpful suggestions in the design and implementation of the Information Breakdown Toolbox.
Disclosure
The authors report no conflicts of interest in this work.
References
Smith MA, Kohn A. Spatial and temporal scales of neuronal correlation in primary visual cortex. J Neurosci. 2008;28:12591–12603. | |
Bair W, Zohary E, Newsome WT. Correlated firing in macaque visual area MT: time scales and relationship to behavior. J Neurosci. 2001;21:1676–1697. | |
Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370:140–143. | |
Panzeri S, Schultz SR, Treves A, Rolls ET. Correlations and the encoding of information in the nervous system. Proc Biol Sci. 1999;266:1001–1012. | |
Nir Y, Fisch L, Mukamel R, et al. Coupling between neuronal firing rate, gamma LFP, and BOLD fMRI is related to interneuronal correlations. Curr Biol. 2007;17:1275–1285. | |
Belitski A, Gretton A, Magri C, et al. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J Neurosci. 2008;28:5696–5709. | |
Mazzoni A, Panzeri S, Logothetis NK, Brunei N. Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput Biol. 2008;4:1–18. | |
Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci. 2003;23:3963–3971. | |
Burns SP, Xing D, Shapley RM. Comparisons of the dynamics of local field potential and multiunit activity signals in macaque visual cortex. J Neurosci. 2010;30:13739–13749. | |
Einevoll GT, Kayser C, Logothetis NK, Panzeri S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat Neurosci Rev. 2013;14:770–785. | |
Averbeck BB, Lee D. Coding and transmission of information by neural ensembles. Trends Neurosci. 2004;27:225–230. | |
Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Neurosci Rev. 2006;7:358–366. | |
Averbeck BB, Lee D. Effects of noise correlations on information encoding and decoding. J Neurophysiol. 2006;95:3633–3644. | |
Shannon CE. A mathematical theory of communication. Bell Labs Tech J. 1948;27:379–423. | |
Magri C, Whittingstall K, Singh V, Logothetis NK, Panzeri S. A toolbox for the fast information analysis of multiple-site LFP, EEG, and spike train recordings. BMC Neurosci. 2009;10:81–105. | |
Quiroga RQ, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat Neurosci Rev. 2009;10:173–185. | |
Destexhe A, Contreras D, Sterlade M. Spatiotemporal analysis of local field potentials and unit discharges in cat cerebral cortex during natural wake and sleep states. J Neurosci. 1999;19:4595–4608. | |
Poort J, Roelfsema PR. Noise correlations have little influence on the coding of selective attention in area V1. Cereb Cortex. 2009;19:543–553. | |
Xiao Y, Wang Y, Felleman DJ. A spatially organized representation of hue in macaque area V2. Nature. 2003;421:535–538. | |
Wang Y, Xiao Y, Felleman DJ. V2 thin stripes contain spatially organized representations of achromatic luminance change. Cereb Cortex. 2007;17:116–129. | |
Lim H, Xiao Y, Wang Y, Hu M, Felleman DJ. Organization of hue selectivity in macaque V2 thin stripes. J Neurophysiol. 2009;102:2603–2615. | |
Wong-Riley MT, Carroll EW. Quantitative light and electron microscopic analysis of cytochrome oxidase-rich zones in V II prestriate cortex of the squirrel monkey. J Comp Neurol. 1984;222:18–37. | |
Xu X, Bosking W, Sary G, Stefansic J, Shima D, Casagrande V. Functional organization of visual cortex in the owl monkey. J Neurosci. 2004;24:6237–6247. | |
Federer F, Williams D, Ichida JM, Merlin S, Angelucci A. Two projection streams from macaque V1 to the pale cytochrome oxidase stripes of V2. J Neurosci. 2013;33:11530–11539. | |
DeYoe EA, Van Essen DC. Segregation of efferent connections and receptive field properties in visual area V2 of the macaque. Nature. 1985;317:58–61. | |
Hubel DH, Livingstone MS. Segregation of form, color, and stereopsis in primate area 18. J Neurosci. 1987;7:3378–3415. | |
Shipp S, Zeki SM. The functional organization of area V2 I: specialization across stripes and layers. Vis Neurosci. 2002;19:187–210. | |
Lu HD, Roe AW. Functional organization of color domains in V1 and V2 of macaque monkey revealed by optical imaging. Cereb Cortex. 2008;18:516–533. |
 © 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.