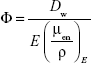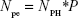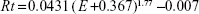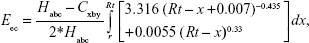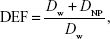Back to Journals » International Journal of Nanomedicine » Volume 11
Monte Carlo and analytic simulations in nanoparticle-enhanced radiation therapy
Authors Paro AD, Hossain M, Webster T , Su M
Received 1 June 2016
Accepted for publication 24 July 2016
Published 16 September 2016 Volume 2016:11 Pages 4735—4741
DOI https://doi.org/10.2147/IJN.S114025
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Carlos Rinaldi
Autumn D Paro,1 Mainul Hossain,2 Thomas J Webster,1,3,4 Ming Su1,4
1Department of Chemical Engineering, Northeastern University, Boston, MA, USA; 2NanoScience Technology Center and School of Electrical Engineering and Computer Science, University of Central Florida, Orlando, Florida, USA; 3Excellence for Advanced Materials Research, King Abdulaziz University, Jeddah, Saudi Arabia; 4Wenzhou Institute of Biomaterials and Engineering, Chinese Academy of Science, Wenzhou Medical University, Zhejiang, People’s Republic of China
Abstract: Analytical and Monte Carlo simulations have been used to predict dose enhancement factors in nanoparticle-enhanced X-ray radiation therapy. Both simulations predict an increase in dose enhancement in the presence of nanoparticles, but the two methods predict different levels of enhancement over the studied energy, nanoparticle materials, and concentration regime for several reasons. The Monte Carlo simulation calculates energy deposited by electrons and photons, while the analytical one only calculates energy deposited by source photons and photoelectrons; the Monte Carlo simulation accounts for electron–hole recombination, while the analytical one does not; and the Monte Carlo simulation randomly samples photon or electron path and accounts for particle interactions, while the analytical simulation assumes a linear trajectory. This study demonstrates that the Monte Carlo simulation will be a better choice to evaluate dose enhancement with nanoparticles in radiation therapy.
Keywords: nanoparticle, dose enhancement, Monte Carlo simulation, analytical simulation, radiation therapy, tumor cell, X-ray
Introduction
Radiation therapy is one of the most commonly used methods for cancer treatments. A challenge for X-ray radiation therapy is that the therapeutic doses used can damage neighboring normal cells. Other than designing better beam techniques, a variety of radiosensitizers (including chemicals, ions, and nanoparticles) have been used to enhance the efficacy of radiation therapy. Because nanoparticles can be functionalized to target ligands expressed at tumor cell surfaces, nanoparticles of heavy atoms have been proposed as promising radiosensitizers for radiation therapy. Owing to high X-ray attenuation coefficient and biocompatibility, gold nanoparticles have been intensively studied as promising candidates to enhance radiation doses.1–3 Secondary electrons and photons released when a photon is incident on a metallic surface are the cause of sensitization. Several interactions can take place between a photon and a metallic surface based on the energy of the photon. These include Compton scattering and photoelectric effects accompanied by photoelectrons and Auger electrons. Compton scattering and photoelectric effects dominate when metallic nanoparticles are used as imaging contrast agents.4,5 As photoelectrons and Auger electrons are released due to the photoelectric effect, they travel through the cell and hydrolyze water molecules creating free radicals that interact with DNA causing DNA damage, and eventually cell death.6,7
Analytical and Monte Carlo methods have been used to calculate the production of secondary electrons in terms of the dose enhancement factor (DEF).8,9 The DEF is defined as the ratio of the average radiation dose absorbed by the tumor when it is loaded with nanoparticles to the dose absorbed without the nanoparticles. Previous analytic calculations were carried out for a single nanoparticle and scaled to account for the total number of nanoparticles attached to a cell surface. The probability of photoelectric interactions, energy balances, and particle transport equations are analytically solved to determine the amount of energy deposited within the cell. The simulation assumes that the nanoparticles are evenly distributed on the cell surface, each nanoparticle has the same probability of interacting with a photon and producing a photoelectron, there are no interactions between secondary electrons and neighboring nanoparticles, and for every electron that leaves the cell, another one enters creating a lateral equilibrium.10 Analytical methods yield solutions that are exactly reproducible between different runs and allow flexibility in changing parameters for any given application. In addition, computations take much less time, milliseconds, compared to Monte Carlo methods, which can take up to hours per run based on geometry complexity. However, analytical techniques are mostly limited to one-dimensional (1-D) space and errors are not easy to estimate.
The second method used to calculate DEF is a Monte Carlo simulation. The Monte Carlo method treats the electron or photon trajectory as a sequence of random steps. Each step is presumed to end in an interaction, chosen through another random sampling. The interactions can cause a change in direction, energy loss, or creation of secondary particles.11,12 All types of physical interactions between matter and radiation can be modeled using Monte Carlo methods for 1-D, 2-D, and 3-D applications. However, high accuracy and resolution require long calculation times. In all cases, Monte Carlo methods suffer from high statistical uncertainties particularly near material boundaries and interfaces. For deep penetration problems or for regions where too few particles contribute to the solution, variance reduction techniques can be used to improve accuracy, but even then the statistical error may be unacceptable.13 Several software packages are available for radiation transport in matter such as GEANT4, MCNP5, and EGSnrc. MCNP5 is a radiation transport code distributed by the Radiation Safety Information Computational Center at Oak Ridge National Laboratory. Written in Fortran 90, this transport code uses a condensed history model.14,15 EGSnrc is a free open-source software package distributed by the National Research Council of Canada. Written in C++, it has an exact boundary crossing algorithm that is used in conjunction with the PRESTA-II transport code.14 GEANT4 is another open-source package written in C++ originally intended for high-energy physics.16 Because of the broad range of applications of GEANT4, the user must supply a physics list that outlines the details of the model.14,17 EGSnrc was decided upon due to it being free open-source software, with its ease of use for user input files, customizable material files, geometry visualization, and documentation.
An issue of these activities is that the results obtained in each group using different methods are largely different. Since each group models a different parameter, it is difficult to compare the soundness of each simulation method. Given the importance of simulation in guiding experiments, it is imperative to find a reliable simulation method with minimum requirements on empirical data. This study intends to compare an analytical simulation based on a 2010 paper10 and a Monte Carlo simulation based on a 2005 paper.18 This study aims to provide, for the first time, a head-to-head comparison between analytical solutions vs Monte Carlo simulations for radiation dose enhancement. It will look into how DEF differs with source energy, nanoparticle materials, and concentration for both analytical and the Monte Carlo simulation.
Methodology
A cell is modeled as a slab of tissue with a single nanoparticle attached to its surface (Figure 1). An analytical and a Monte Carlo simulation were compared for various source energies, nanoparticle materials, and concentrations. Endothelial cell lines of tumor vasculature are more likely to be exposed to nanoparticles. For both simulations, an endothelial cell was modeled as a 10×10×2 μm slab composed of 10% hydrogen, 11% carbon, 2% nitrogen, and 76% oxygen according to the International Commission on Radiation Units and Measurements. X-ray energies from 10 to 900 keV were chosen to model the low-energy photon beam. Nanoparticle concentrations of 5, 10, 15, and 20 mg/g of tissue, evenly distributed through the cell, were chosen based on their usage in literature. Both simulations were performed for gold, bismuth, silver, and copper.
  | Figure 1 Analytical simulation scheme, where a single nanoparticle is at the center of a cell modeled as a slab of tissue. |
Analytical simulation
The analytical simulation modeled a single nanoparticle with radius of r, at the center of a cell. Dose enhancement was calculated using the equations presented in the 2010 Ngwa et al paper and the 2012 Hossain and Su paper.9,10 For these equations, a base dose, Dw =2 Gy, chosen based on its clinical relevance, and a monoenergetic beam were used to calculate the photon fluence (Φ):
|
|
and the number of photons interacting with a single nanoparticle, Nph = Φ*π*r2, where (μen/ρ)E is the mass absorption of coefficient of water at a given photon energy E, and r is the nanoparticle radius. On the basis of the probability of a photoelectric interaction, P ≈ (μpe/ρ)E*ρNP*dNP, where dNP is the average distance a photoelectron travels through the nanoparticle, ρNP is the nanoparticle density, and (μpe/ρ)E is the photoelectric absorption coefficient of the nanoparticle at energy E. The total number of photoelectrons produced per nanoparticle is calculated using the following equation:
|
|
Based on the energy of the photoelectron, Epe = E – Eedge, the maximum distance traveled through the cell is:
|
|
The energy deposited within the cell, per photoelectron is calculated using the following equation:
|
|
where Habc = 2*π*R(0.5*t)2, Cxby = 2*π*Rt*(Rt –0.5t), with t being the thickness of the cell. This equation assumes evenly distributed nanoparticles and equilibrium between secondary electrons leaving and entering the cell. This is then scaled by the total number of photoelectrons released, NPet = NPE*NNP, where NNP is the total number of nanoparticles in the cell, to get the total energy deposited in the cell, Eect = Eec*Npet. The DEF is then
|
|
where DNP = Eect/mcell is the dose deposited from the photoelectrons.
Monte Carlo simulation
EGSnrc provided by the National Research Council of Canada was used as the basis for the Monte Carlo simulation. EGSnrc is an electron transport code that comes equipped with electron transport in matter, tracking for individual electrons and photons. Using Tutor7pp as a base, the code was modified to allow for photoelectric interactions, atomic relaxations resulting in Auger electrons, and Compton interactions. Tutor7pp is a standard code with the EGSnrc distribution that uses analog scoring to calculate energy deposition in each region along with energy reflected and transmitted through the geometry.14 The code was modified to tag and track photoelectrons, Auger electrons, Compton photons, or Compton electrons. If the tracked particle deposited its energy within the cell, its type and energy was outputted to a file and the energy was scored in a bin based on its type. After the simulation was complete, the code exported the energy deposited by Compton photons and electrons, Auger electrons, photoelectrons as well as the total energy deposited in the cell.
Four-component International Commission on Radiation Units and Measurements tissue was used as the base material for the cell, and the composition and density were altered for the different concentrations. Pegs4 was used to generate the material pegs file needed for the simulation. The cell was irradiated with photons using a parallel beam with a Gaussian distribution. The beam cross-section was 10×10 μm2, had a full width at half maximum of 10, and varying mean energies. The global electron cutoff energy was set to 0.7 MeV, and the global photon cutoff energy was set to 0.01 MeV. DEF was calculated for each energy by dividing energy deposited in the cell with nanoparticles by energy deposited in the cell without nanoparticles for the same number of photon instances. The number of photon instances that provided a base dose of 2 Gy was used for each photon energy.
Results and discussion
Low-energy beams, ≤200 kV, with a penetration depth of ≤5 mm have limited applications and are mainly used for surface treatment of the skin. Medium energies 200 kV–1 MV (orthovoltage and supervoltage X-rays) are used for shallow treatments, while greater high-energy beams from 1 to 25 MV are used for treating deeply buried (>2 cm in depth) tumors.19
Figure 2A shows the results from analytical simulation, where DEFs as a function of source energy for copper, silver, gold, and bismuth nanoparticles are calculated. X-ray beams used for medical treatment are polyenergetic where the high-energy spectra have a low-energy component. At lower energies, X-ray matter interactions are dominated by the photoelectric effect, whereas the high-energy component interacts with matter by Compton scattering. The photoelectric effect is most effective until the photon energy from the external beam reaches a certain maximum that depends on the specific material under consideration. The interaction probability between the source photons and the nanoparticles, as well as the energy transfer coefficient in the medium, increases with decreasing source energy and increasing atomic number of the nanoparticles. The photoelectric cross-section varies as Z4 or Z5, where Z is the atomic number of the nanoparticle and is enhanced by an increased absorption by electron shells (K, L, M, etc) at low energies. The photoelectric effect is followed by the emission of an X-ray photon or an Auger electron. The Auger effect is mostly seen in Z<15 materials and is almost absent in materials with Z>60.19
In materials with higher atomic numbers, such as gold and bismuth, there are two peaks corresponding to the K and M edge energies. Silver only has one peak, which corresponds to the L edge energy, while copper does not have these peaks. The peaks occur when the photon energy exceeds the edge energy and begins ionizing a different electron shell. Peaks near the edge energies support the theory that at low energies, photoelectrons and Auger electrons have a shorter trajectory in tissue, and therefore are more likely to deposit all of their energy in the cell. For high energies, the analytical simulation predicts a DEF of 1, ie, no enhancement, for all materials.
Figure 2B shows the results from the Monte Carlo simulation, where DEF varies as a function of energy for copper, silver, gold, and bismuth. For the energies of interest, the Monte Carlo simulation predicts a Gaussian distribution for the DEF, with a maximum at around 90 keV for gold and bismuth and 50 keV for silver and copper. The Monte Carlo simulation also predicts that at high energies the DEF levels out around 1.2 for copper and upward of 1.6 for gold. This is because the Z-dependent probability of the photoelectric effect gets smaller at the higher MeV ranges, where the Compton interaction starts to dominate. In Compton scattering, which is independent of Z, incoming X-rays eject an electron from the atom and scatters a photon. The scattered photon, depending on its energy, can further induce the photoelectric or Compton effect as well as generate secondary electrons. Secondary electrons generated by keV X-rays from the nanoparticle surface have lower energy, a shorter trajectory, and higher energy transfer rate to the surroundings, which in turn results in a higher DEF value.
Figure 3A–D shows a direct comparison between the analytical and Monte Carlo simulation for various materials at a concentration of 20 mg/g. For each material, the analytical and Monte Carlo simulations predict vastly different DEF values. One major difference is at high energies where the analytical simulation does not predict an enhancement (DEF =1), the Monte Carlo simulation does. One reason for this is in the limitations of the analytical simulation. The analytical simulation does not account for photoelectron interactions with neighboring nanoparticles. Since the Monte Carlo takes a random sampling for each trajectory step, it accounts for interactions with neighboring nanoparticles. These interactions could change the trajectory of the photoelectrons and Auger electrons, reduce the electrons energy, or cause another photoelectron or Auger electron to be ejected. In all the cases, the Monte Carlo simulation would continue to track its trajectory until all the energy is deposited within the cell. The analytical simulation on the other hand assumes a linear trajectory of the electron with a set probability of depositing the energy within the cell. The discrepancy at low energies may be due to the analytical simulation not accounting for recombination.
Finally, DEF was calculated as a function of energy for various concentrations of gold nanoparticles. Figure 4A shows the results from the analytical simulation, while Figure 4B shows the results from the Monte Carlo simulation. Both simulations predict an increase in DEF as the concentration increases, although the increase in the Monte Carlo simulation is larger than the increase in the analytical simulation for larger energies. At 10 keV, the Monte Carlo simulation does not predict concentration dependence. This may be due to several factors including recombination, which is accounted for in the Monte Carlo simulation.
  | Figure 4 The relationship between DEF and concentration for the (A) analytical simulation and (B) the Monte Carlo simulation. |
Conclusion
Nanoparticles of high atomic number elements could be used to enhance X-ray radiation therapy. Although both analytical and the Monte Carlo simulations predict an increase in dose enhancement in the presence of nanoparticles, the two methods do not give comparable results for few reasons.
- The Monte Carlo simulation takes into account energy deposited by photoelectrons, Auger electrons, Compton photons and Compton electrons, and source photons, while the analytical one calculates energy deposited by source photons and photoelectrons.
- The Monte Carlo simulation accounts for electron–hole recombination while the analytical simulation does not.
- Monte Carlo simulation randomly samples the photon or electron path and accounts for particle interactions, while the analytical simulation assumes a linear trajectory.
This work demonstrates that for varying nanoparticle material, concentration, and X-ray beam conditions, the Monte Carlo simulations present a more comprehensive approach to calculate DEFs. Future works should involve improving the analytic simulation by adding in the Auger electron spectrum, taking into account the relaxation effects, and simulating discrete nanoparticles within the cell. Validation of the two simulations should be conducted through experiments carried out in phantoms or mice.
Acknowledgment
This project is supported by a Director’s New Innovator Award from National Institute of Health to Ming Su (1DP2EB016572).
Disclosure
The authors have no conflicts of interest to disclose.
References
McMahon SJ, Hyland WB, Muir MF, et al. Biological consequences of nanoscale energy deposition near irradiated heavy atom nanoparticles. Sci Rep. 2011;1:18. | ||
Kwatra D, Venugopal A, Anant S. Nanoparticles in radiation therapy: a summary of various approaches to enhance radiosensitization in cancer. Transl Cancer Res. 2013;2(4):330–342. | ||
Chithrani DB, Jelveh S, Jalali F, et al. Gold nanoparticles as radiation sensitizers in cancer therapy. Radiat Res. 2010;173(6):719–728. | ||
Mesbahi A. A review on gold nanoparticles radiosensitization effect in radiation therapy of cancer. Rep Pract Oncol Radiother. 2010;15(6):176–180. | ||
Hainfeld JF, Dilmanian FA, Slatkin DN, Smilowitz HM. Radiotherapy enhancement with gold nanoparticles. J Pharm Pharmacol. 2008;60(8):977–985. | ||
Lee C, Cheng NN, Davidson RA, Guo T. Geometry enhancement of nanoscale energy deposition by x-rays. J Phys Chem C. 2012;116(20):11292–11297. | ||
Carter JD, Cheng NN, Qu Y, Suarez GD, Guo T. Nanoscale energy deposition by X-ray absorbing nanostructures. J Phys Chem B. 2007;111(40):11622–11625. | ||
Berbeco RI, Ngwa W, Makrigiorgos GM. Localized dose enhancement to tumor blood vessel endothelial cells via megavoltage X-rays and targeted gold nanoparticles: new potential for external beam radiotherapy. Int J Radiat Oncol Biol Phys. 2011;81(1):270–276. | ||
Hossain M, Su M. Nanoparticle location and material dependent dose enhancement in X-ray radiation therapy. J Phys Chem C Nanomater Interfaces. 2012;116(43):23047–23052. | ||
Ngwa W, Makrigiorgos GM, Berbeco RI. Applying gold nanoparticles as tumor-vascular disrupting agents during brachytherapy: estimation of endothelial dose enhancement. Phys Med Biol. 2010;55(21):6533–6548. | ||
Salvat F, Fernandez-Varea JM, Sempau J. Penelope-2008: a code system for monte carlo simulation of electron and photon transport. Paper presented at: Oganisation for Economic Co-Operation abd Development; 2008; Barcelona, Spain. | ||
Andreo P. Monte Carlo techniques in medical radiation physics. Phys Med Biol. 1991;36(7):861–920. | ||
Garth JC. Electron/photon transport and its applications. Poster Presented at: American Nulcear Society Topical Meeting in Monte Carlo; April; 2005; Chattanooga, TN. | ||
Archambault JP, Mainegra-Hing E. Comparison between EGSnrc, Geant4, MCNP5 and Penelope for mono-energetic electron beams. Phys Med Biol. 2015;60(13):4951–4962. | ||
Lechtman E, Chattopadhyay N, Cai Z, Mashouf S, Reilly R, Pignol JP. Implications on clinical scenario of gold nanoparticle radiosensitization in regards to photon energy, nanoparticle size, concentration and location. Phys Med Biol. 2011;56(15):4631–4647. | ||
Amato E, Italiano A, Leotta S, Pergolizzi S, Torrisi L. Monte Carlo study of the dose enhancement effect of gold nanoparticles during X-ray therapies and evaluation of the anti-angiogenic effect on tumour capillary vessels. J Xray Sci Technol. 2013;21(2):237–247. | ||
Faddegon BA, Kawrakow I, Kubyshin Y, Perl J, Sempau J, Urban L. Accuracy of EGSnrc, GEANT4 and PENELOPE Monte Carlo systems for simulation of electron scatter in external beam radiotherapy. Phys Med Biol. 2009;54(20):6151–6163. | ||
Cho SH. Estimation of tumour dose enhancement due to gold nanoparticles during typical radiation treatments: a preliminary Monte Carlo study. Phys Med Biol. 2005;50(15):163–173. | ||
Retif P, Pinel S, Toussaint M, et al. Nanoparticles for radiation therapy enhancement: the key parameters. Theranostics. 2015;5(9):1030–1044. |
 © 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.