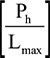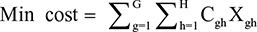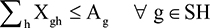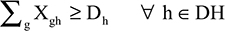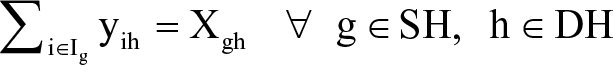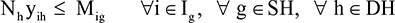Back to Journals » Journal of Healthcare Leadership » Volume 10
Model for allocation of medical specialists in a hospital network
Authors Suppapitnarm N , Pongpirul K
Received 28 February 2018
Accepted for publication 30 May 2018
Published 6 September 2018 Volume 2018:10 Pages 45—53
DOI https://doi.org/10.2147/JHL.S166944
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Russell Taichman
Nantana Suppapitnarm,1,2 Krit Pongpirul1,3,4
1Department of Preventive and Social Medicine, Faculty of Medicine, Chulalongkorn University, Bangkok, Thailand; 2Medical Affairs Office, Bangkok Dusit Medical Services Public Company Limited, Bangkok, Thailand; 3Department of International Health, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA; 4Thailand Research Center for Health Services System (TRC-HS), Faculty of Medicine, Chulalongkorn University, Bangkok, Thailand
Introduction: As human diseases are becoming increasingly complex, the need for medical specialist consultation is more pronounced, and innovative ways to allocate medical specialists in hospital networks are essential. This study aimed to construct allocation models using a multi-objective programming approach in a large private hospital network in Thailand.
Methods: Our study included 13 medical specialist types in four main disease groups of the Bangkok Dusit Medical Services network. Mixed-integer linear programming models were developed using inputs from a modified Delphi survey of executives, the Physician Engagement Survey, and the Physician Registry (PR) databases and featuring three objectives: 1) minimizing travel expense, 2) optimizing physician engagement, and 3) maximizing the chance of direct patient encounters with respective medical specialists who were formally qualified for the clinical complexity of the patients, as measured by the case mix index (CMI).
Results: The constructed models included the core components but varied by a combination of whether part-time medical specialists are included or not (noPT) and whether CMI is included (CMI) or not (noCMI). Because the noPT + CMI model had the highest capability to solve for specialist allocation, it was further improved for some specialist types in terms of flexibility for sensitivity analysis of the variables. Moreover, to assess the feasibility and practicality of the models, a web-based system incorporating the final model was developed to support the central executives’ decision to allocate medical specialists to the network, especially for finding the most optimal and timely solution for widespread shortages.
Conclusion: The linear programming models that accommodate critical components for allocating medical specialists in the hospital network were feasible and practical for the central executives’ timely decision making. The models could be further tested for their application in hospitals in the public sector or other private hospital networks.
Keywords: medical specialist, allocation, linear programming, human resource planning
Introduction
Human resources are one of the most complex and costly components facing the health care industry;1 inefficient management would lead to inequitable health outcomes for high-risk, rural populations and remote area communities.2,3 Although complex clinical conditions and emerging diseases warrant a greater need for specialized care, the quantity and distribution of medical specialists have been of concern.4,5
Many industries have been successful in utilizing shared resources within a network or reallocating resources within a merged network to address these concerns. Connor et al studied the results of mergers and acquisitions in health networks and found that higher merger rates are related to cost savings of lower occupancy hospitals.6 Sherman and Rupert demonstrated that the merger of four branches contributed to a reduction in operating costs by reducing the occupancy rate.7 In addition, placement models are a very popular method for providing sanitation services,8 and many studies have sought to reduce travel costs, such as those by Chu and Chu,1 Galvão et al,9 Gunes and Yaman,10 and Chaovalitwongse et al.11
Efficient allocation of medical specialists across hospitals in a network requires not only demand information (eg, patient complexity and hospital expansion), but also physicians’ willingness to be placed at unanticipated sites. Although this scenario is rather common in a public-dominated health care system, evidence on how to promote an efficient allocation of medical specialists has been lacking. In general, a hospital that encounters complicated and resource-intensive patients requires a specialist. To address this, the case mix index (CMI) was developed to reflect the diversity, clinical complexity, and resource needs of all patients in a hospital. CMI for a hospital is the average relative diagnosis-related group weight of a hospital’s inpatient discharges, calculated by summing the Medicare severity-diagnosis-related group weight for each discharge and dividing the total by the number of discharges. For example, a hospital with a CMI of 2.0 for patient care per 1000 patients compared to a hospital with a CMI of 1.0 for patient care per 1000 patients is twice as likely to use more resources and would have a higher incidence of sicker patients. CMI is one of the factors that influences resource management, as reported by Kalisch et al.12
As a commonly used term in health care management, physician engagement is the process of bringing physicians together with other health care stakeholders to improve care and the patient experience on a continuous basis. It is measured by physicians’ increased satisfaction and loyalty to their affiliated organizations, as well as better alignment of key cost and quality improvements. Engaging physicians in this sense are those who are committed to the organization’s mission and are willing to help the organization when required. Organizations that achieve a high percentage of physician engagement are likely to succeed in their operations as the physicians are willing to help and are committed to a shared responsibility.
Bangkok Dusit Medical Services (BDMS), currently with 32 hospitals, is a large hospital network in the Asia-Pacific region. With 14 Joint Commission International-accredited hospital programs and clinical care program certification, BDMS has delivered world-class care to an international clientele, providing top-tier services and facilities and skilled specialists in every field. Government Savings Bank’s research forecasted that, with the introduction of Association of Southeast Asian Nations (ASEAN) Economic Community along with the government’s policy of promoting Thailand as the medical hub of ASEAN, efforts to increase health awareness, and Thailand rapidly becoming an aging society, the private hospital industry would continue to grow in 2016 in line with the economic growth. As a result of the growth in medical tourism, health awareness, and the aging population, BDMS’s targeted customers in 2016 are the health conscious, the elderly, medical tourists, and expatriates.13
We can apply linear programming (LP), a widely known operations research technique, to optimally allocate available resources such as doctors, dentists, and nurses to fit the needs of hospitals as well as in emergency or disaster situations. For example, Chaovalitwongse et al allocated physicians, dentists, and nurses by launching mobile health services;11 Sheu studied the allocation of transport facilities in response to disasters;14 Vaziri et al examined the allocation of physicians for trauma patient care;15 and Swangnop and Chaovalitwongse studied the allocation of medical personnel to many clinics and their ability to manage work time.16 Currently, to the best of our knowledge, no research has explored specialist allocation that integrates the complexity of patients using CMI in the major diseases that affect death rates, such as cancer, heart disease, cerebral palsy, and accidental emergencies within a hospital network. This paper attempts to tackle this important problem to best manage and utilize these qualified physicians to save lives in the most effective manner.17 With the increasing severity and complexity of diseases facing our population as well as rising costs, our experience with this model development might be useful for hospital networks in the public sector as well as other private hospital networks.
Methods
Identification of potential determinants using a modified Delphi survey
We performed a four-round modified Delphi survey with all executives to identify potential determinants that might influence decisions about allocating medical specialists with respect to the demand areas.18 The questionnaire for this study was developed based on 46 key points identified from published literature and was reviewed by experts from both public and private sectors for face validity. The first round was conducted among all 32 representative hospitals of the BDMS network. Each nominated executive was emailed a cover letter outlining the objective of the study along with the six-page questionnaire, comprising two parts: 1) the demographic data (gender, age, education, job position, and administrative experience) and 2) the degree to which each item could influence their decision to allocate medical specialists, using a 5-point Likert scale. Three additional rounds of the survey were then conducted. Items with expanding standard deviations or inconsistent values across the four rounds were considered unreliable and, therefore, excluded. The items that remained at the fourth round will be considered as potential determinants.
This study was approved by the Institutional Review Board of the Faculty of Medicine, Chulalongkorn University (IRB No 387/2558) and the Institutional Review Board of Bangkok Hospital Headquarters (IRB No 2015-09-044). All participants provided written informed consent.
Analysis of Physician Engagement Survey (PES) and Physician Registry (PR) databases
PES
Physician engagement has been part of the BDMS management for the past decade. In 2012, the questionnaire was developed based on Gallup19 by our human resource department, using the following procedures. First, key potential points identified from published literature that were also relevant to our context were proposed. The initial draft was presented to all top-ranked medical executives in our network. Forty-five items that might influence physician engagement were identified and included in the 5-point Likert scale questionnaire. Based on the feedback from all medical staff during the pilot survey, the number of items were reduced to 38 with very high internal consistency (Cronbach’s alpha 0.981). Engaged physicians in this sense are those who are committed to the organization’s mission and are willing to help the organization when required. Within our network, in May of each year since then, we have evaluated physician engagement by asking them to respond to the 38-item PES questionnaire and converted the results into an overall percentage score. In our model herein, given the overall mean of 70% engagement from the 2012–2016 survey, we decided that only medical specialists with a physician engagement score of ≥70% should be included in the present study.
PR
This database contains demographics, clinical credentials, and practice characteristics of all medical doctors in 13 medical specialties (cardiology, interventional cardiology, cardiothoracic surgery, interventional radiology, neurosurgery, neurology, orthopedics, anesthesiology, ophthalmology, oncology, breast surgery, surgical oncology, and radiotherapy) who work at each of the hospitals in the network. Monthly data were submitted by individual hospitals to the main database. Although the network comprised 38 hospitals, unsatisfactory assessment of data quality resulted in the exclusion of six hospitals from the analysis. The demand was represented by the total number of outpatient, inpatient, and surgical cases divided by the number of patients for whom a doctor can be responsible.
LP models
We formulated five mixed-integer linear programming (MILP) models representing different varieties of a basic model for allocating the 13 specialties to four disease groups. The aim was to find the best possible resource allocation solution that would not only minimize total transportation costs, but also maximize physician engagement and patients’ needs. The key input variables for our models were selected from the three sources described above: physician engagement from PES, physician characteristics from PR, and potential determinants from the Delphi survey. The selected potential determinants were, 1) health needs of the population (defined by the number of physicians within the network and number of patients, including patients’ needs), 2) severity of patients’ conditions, 3) complexity of patients’ conditions (defined by the CMI), 4) organization’s mission, 5) organization’s Hoshin Kanri (policy deployment) 6) organization’s strategy. However, the last three factors (Mission, Hoshin and Strategy) were not included in the model because all the hospitals within the network were with BDMS for at least a year and received the same mission, vision, and strategies from the top executives of BDMS, and technically, they were difficult to quantify.
Model testing
To assess the feasibility and practicality of the models, a web-based medical specialist allocation (MSA) platform incorporating the final model was developed to support the central executives’ decision to allocate medical specialists to the network, especially for finding the most optimal and timely solution for widespread shortages. Another questionnaire was developed based on the context, input, process, and product evaluation model in order to determine a program’s value to the five top executives as well as provide additional comments with regard to the model. The optimization (ie, cost reduction) ability of the chosen model for variations of decision parameters, especially the number of patients and disease severity, was assessed.
Results
Identification of potential determinants using the modified Delphi survey
Forty-three executives participated in the first round of the Delphi survey; the number of participants in successive rounds gradually decreased to 31. Of the 46 issues identified from the reviews and interviews, 11 with inconsistent values were removed and 35 factors were considered potential determinants of MSA. For input parameters of the LP model, we focused on the means of factors in the survey that were >4.5 and with an interquartile range of <1.5. The six factors that hospital executives ranked highest were health needs of population, organization’s mission, organization’s Hoshin, organization’s strategy, and severity and complexity of patients’ conditions (Table 1).
  | Table 1 Factors influencing the allocation of medical specialists Notes: *“Hoshin Kanri (also called Policy Deployment) is a method for ensuring that the strategic goals of a company drive progress and action at every level within that company. This eliminates the waste that comes from inconsistent direction and poor communication. Hoshin Kanri strives to get every employee pulling in the same direction at the same time. It achieves this by aligning the goals of the company (strategy) with the plans of middle management (tactics) and the work performed by all employees (operations).”26 Abbreviations: OPD, outpatient department; IPD, inpatient department. |
Analysis of PES and PR databases
Of 2587 medical specialists in the PR database, 569 were full-time; of these, 517 with high physician engagement scores were included in the model. The overall numbers of medical specialists were sufficient for the demand across the network. The number of full-time medical specialists was still inadequate for seven specialties: oncology, ophthalmology, radiotherapy, breast surgery, surgical oncology, interventional cardiology, and interventional radiology.
LP models
Assuming that the costs associated with assigning 13 specialties to each of the 32 hospitals are different, the basic MILP model is described in the Supplementary materials. In principle, these deterministic objective force models deal with three “sets of things”: supplying hospitals, demanding hospitals, and medical specialists to be transferred, each of which was denoted by using “indices” (ie, hospital g supplies doctor i to hospital h). In order to reach three main objectives (minimizing expense, optimizing physician engagement, and maximizing the chance of direct patient encounters with qualified medical specialists), the “parameters” selected from the methods described above behave like inputs for the models whereas outputs are produced and presented in the “variables” (ie, number of doctors that should be sent from hospital g to hospital h). As travel cost is the most critical component of the expense, the expense required for traveling between two nearby hospitals was used. To optimize physician engagement, the models transferred only highly engaged physicians. To ensure clinical care quality, the models transferred physicians from hospitals with higher CMI to hospitals with lower or equal CMI.
The five MILP models included travel expenses and physician engagement level, but varied by a combination of whether or not part-time medical specialists are included and whether or not CMI is included as shown in Table 2.
Model testing
Based on the feasibility and practicality reported by the top executives, model 5, implemented in the MSA platform (Figure 1), was the preferred model for allocating medical specialists within our hospital network. The sensitivity analysis revealed that even when >50% of the specialists were transferred between hospitals to address the change in the number of patients and disease severity, the model still has good optimization ability. In the current usage, when trying to choose a doctor in a particular field (eg, oncology) for a hospital in need, the model can allocate exactly that. The model would select appropriate physicians with appropriate experiences and skills to take care of complex patient cases. For less complicated illnesses, the model would assign doctors to nearer hospitals first, before hospitals with increasing distance and cost. The system could propose some preliminary what-if scenarios before deciding to send a doctor, which is a reasonable practice. Another usage that top executives agreed on is that the web-based tool can be used to strengthen doctor skills by sending low-CMI doctors to high-CMI hospitals to learn about more complex cases. These doctors can gain valuable experiences, which can help them further in their careers. However, our model has a limitation if applied to new physicians, as some physician characteristics and their CMI may not be fulfilled because they have not worked with BDMS during the primary survey.
  | Figure 1 Web-based MSA platform. Abbreviations: MSA, medical specialist allocation; CMI, case mix index. |
Discussion
This operational research exemplifies the use of the LP technique for allocating medical specialists in a large hospital network. We developed a basic MILP model to allocate full-time and part-time medical specialists using a common health care parameter called CMI, reflecting a physician’s expertise to handle a patient’s case at a particular hospital that needs a medical specialist. We developed five variations of the basic optimization model and constructed a web-based system that allows the cost analysis of the decision to send specialists to various hospitals within our network.
Previous studies used LP models for human resource management in the health care sector. However, they focused only on mapping the patients’ requirements with the available physicians whereas heuristic principles should be employed in decision making as only mathematical models cannot provide solutions for physician allocation (Swangnop and Chaovalitwongse,16 Chaovalitwongse et al,11 and Stummer et al20). On the contrary, our study takes into account specific patients’ needs according to their severity and complexity of the diseases, and attempted to allocate the best available specialists for optimal care at their respective hospitals. This was different from the previous studies by Abedian et al21 and Mascia et al22 that had to refer the patients to tertiary centers or to available hospitals which had potential for appropriate treatment. It is interesting to note that our study also included physician willingness as one of the variables for such an allocation process as we believe that this would raise organizational engagement which was the key to success for the health care business. By adding more complex, but relevant variables, the models could help solve the problem of allocation of specialists within the network. We also adjusted those variables according to their importance with the help of the web-based BDMS-MSA. Therefore, such an allocation process is efficient not only for satisfying the hospitals that demand specialists, but also for reducing traveling cost. The web-based platform that we developed has been used for decision making in real time, which is an optional functionality for settings with promptly available data.
The company’s strategic vision is to expand throughout the country as well as internationally through mergers and acquisitions approach. The system described in this paper is an attempt to concurrently optimize the allocation of medical specialists and travel expense. Management has set a certain target for cost reduction while maintaining the quality of health care. By analyzing one medical specialty at a time, we found that, under the current operating environment, the first four models could only partially solve the allocation problem satisfactorily. However, by allowing the top management to interact with the web-based decision support system and adjust the priorities of CMI, physician engagement, and travel expense, model 5 could allocate all medical specialties and meet the cost reduction targets. Our findings concur with that of Kang et al,23 Branas et al,24 and Nukala and Balaji25 in that operations research is a useful tool to manage the MSA process for a hospital network due to the complex decision-making process. For future study, we recommend incorporating more sophisticated priority-setting models. Also, the models should be further tested in other public and private hospitals.
Conclusion
The LP models that accommodate critical components for allocating medical specialists in the hospital network were feasible and practical for timely decision making by the central executives. The models could be further tested for their application in hospitals in the public sector or other private hospital networks.
Acknowledgments
This research was supported by Bangkok Dusit Medical Services PCL. We gratefully acknowledge Lindo Systems, Inc. (www.lindo.com), for providing free access to What’s Best! software for optimization work. The authors also thank Dr Pricha Pantumsinchai of M-Focus Co, Ltd (www.m-focus.co.th), for his valuable guidance in preparing this paper.
Disclosure
The authors report no conflicts of interest in this work.
References
Chu SCK, Chu L. A modeling framework for hospital location and service allocation. Int Trans Oper Res. 2000;7(6):539–568. | ||
World Health Organization. Increasing Access to Health Workers in Remote and Rural Areas Through Improved Retention: Global Policy Recommendations. Geneva: WHO; 2010. Available from: https://www.ncbi.nlm.nih.gov/books/NBK138618/. Accessed January 31, 2018. | ||
Dussault G, Franceschini MC. Not enough there, too many here: understanding geographical imbalances in the distribution of the health workforce. Hum Resour Health. 2006;4:12. | ||
Lewis CL, Wickstrom GC, Kolar MM, et al. Patient preferences for care by general internists and specialists in the ambulatory setting. J Gen Intern Med. 2000;15(2):75–83. | ||
Madu AJ, Ubesie A, Madu KA, Nonyelu C, Ibegbulam OG. Medical specialist preferences and reasons among fresh nigerian interns. Ann Med Health Sci Res. 2014;4(Suppl 3):S223–S227. | ||
Connor RA, Feldman RD, Dowd BE, Radcliff TA. Which types of hospital mergers save consumers money? Health Aff (Millwood). 1997;16(6):62–74. | ||
Sherman HD, Rupert TJ. Do bank mergers have hidden or foregone value? Realized and unrealized operating synergies in one bank merger. Eur J Oper Res. 2006;168(1):253–268. | ||
Rahman S-U, Smith DK. Use of location-allocation models in health service development planning in developing nations. Eur J Oper Res. 2000;123(3):437–452. | ||
Galvão RD, Acosta Espejo LG, Boffey B. A hierarchical model for the location of perinatal facilities in the municipality of Rio de Janeiro. Eur J Oper Res. 2002;138(3):495–517. | ||
Gunes ED, Yaman H. Health network mergers and hospital re-planning. J Oper Res Soc. 2009;61(2):275–283. | ||
Chaovalitwongse P, Somprasonk K, Phumchusri N, Heim J, Zabinsky ZB, Chaovalitwongse WA. A decision support model for staff allocation of mobile medical service. Ann Oper Res. 2017;249(1–2):433–448. | ||
Kalisch BJ, Friese CR, Choi SH, Rochman M. Hospital nurse staffing: choice of measure matters. Med Care. 2011;49(8):775–779. | ||
Bangkok Dusit Medical Services. Annual Report; 2016. Available from: http://bdms.listedcompany.com/misc/ar/20170313-bdms-ar2016-en-03.pdf. Accessed March 20, 2017. | ||
Sheu J-B. An emergency logistics distribution approach for quick response to urgent relief demand in disasters. Transport Res E Log Transport Rev. 2007;43(6):687–709. | ||
Vaziri K, Roland JC, Robinson L, Fakhry SM. Optimizing physician staffing and resource allocation: sine-wave variation in hourly trauma admission volume. J Trauma. 2007;62(3):610–614. | ||
Swangnop S, Chaovalitwongse P. Joint requirement of two multi-skill resource types in multi-period multi-site assignment problem. Eng J. 2015;19(1):15. | ||
Buchan J, Dal Poz MR. Skill mix in the health care workforce: reviewing the evidence. Bull World Health Org. 2002;80(7):575–580. | ||
Macmillan T. The Delphi technique. Paper presented at: The Annual Meeting of the California Junior Colleges Association Commission on Research and Development; May 3; 1971; Monterey, CA. | ||
Blizzard R. Physician engagement is built, not bought. 2004. Available from: http://news.gallup.com/poll/11503/physician-engagement-built-bought.aspx. Accessed January 31, 2018. | ||
Stummer C, Doerner K, Focke A, Heidenberger K. Determining location and size of medical departments in a hospital network: a multiobjective decision support approach. Health Care Manag Sci. 2004;7(1):63–71. | ||
Abedian S, Kazemi H, Riazi H, Bitaraf E. Cross hospital bed management system. Stud Health Technol Inform. 2014;205:126–130. | ||
Mascia D, Angeli F, Di Vincenzo F. Effect of hospital referral networks on patient readmissions. Soc Sci Med. 2015;132:113–121. | ||
Kang D, Jung J, Bae D-H. Constraint-based human resource allocation in software projects. Softw Pract Exp. 2011;41(5):551–577. | ||
Branas CC, MacKenzie EJ, ReVelle CS. A trauma resource allocation model for ambulances and hospitals. Health Serv Res. 2000;35(2):489–507. | ||
Nukala V, Balaji K. Resource Allocation for Healthcare Organizations: Proceedings of 2011 IEEE Conference on Automation Science and Engineering (CASE). Institute of Electrical and Electronics Engineers (IEEE), Piscataway, NJ, USA: 24-27 August; 2011; Trieste, Italy. | ||
What is Hoshin Kanri? [webpage on the Internet]. Available from http://www.leanproduction.com/hoshin-kanri.html. Accessed January 31, 2018. |
Supplementary materials
Mixed-integer linear programming (MILP) models
Sets
SH | Supplying hospitals or resources, G = |SH| | |
DH | Demanding hospitals, H = |DH| | |
Ig | List of transferrable doctors with the specialty at resource g |
Indices
g | Resource or hospital providing medical specialists, g=1, 2, …, G | |
h | Hospital that needs medical specialists, h=1, 2, ..., H | |
i | Doctor or medical specialist | |
% Growth | Percentage of patient increase each year |
Parameters
Ag | Available number of doctors with the specialty at hospital g, |Ig| | |
Ph | Number of patients requiring specialty doctors at hospital h | |
Lmax | Maximum number of patients who can be treated by a doctor with the specialty | |
Dh | Number of doctors with the specialty needed at hospital h, where Dh = % Growth | |
Cgh | Transportation cost for sending a specialist from hospital g to hospital h | |
Mig | Case mix index (CMI; reflects the diversity, clinical complexity, and need for resources in the population of all patients) of doctor i at resource g with the specialty | |
Nh | CMI (reflects the diversity, clinical complexity, and need for resources in the population of all patients) of demanding hospital h needing the specialty |
Variables
Xgh | Number of doctors with the specialty that should be sent from hospital g to hospital h | |
|
Model
The model ensures that the medical specialist is allocated to meet the hospital requirement while minimizing travel expenses. For ease of implementation, we assume that the model is optimized separately for each medical specialty. Thus, the mathematical formulation for medical specialist allocation can be expressed as follows.
| (1) |
subject to
| (2) |
| (3) |
| (4) |
| (5) |
In determining specialist availability, each full-time doctor was counted as one doctor and each part-time doctor was counted as 0.5 doctors. Of all doctors included in the model, only doctors with physician engagement ≥70% were chosen. The objective function in Equation 1 is to minimize the travel expenses of all medical specialist allocation. Equation 2 represents the supply constraints, requiring the total number of medical specialists allocated to all needed sites to not be higher than that available at supplying hospital g. Equation 3 shows the demand constraints, requiring the total number of medical specialists from all supplying hospitals to be at least equal to that requested by hospital h. Equation 4 calculates the number of selected doctors from supplying hospital g who will be assigned to help hospital h. Finally, Equation 5 requires that each doctor’s skill or capability to treat difficult patients, represented by the CMI of each medical specialist, must be higher than the CMI of the needed hospital.
 © 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2018 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.