Methylation as an epigenetic source of random genetic effects in the classical twin design

Introduction

The classical twin design is an important tool in the study of the genetics of complex (non-Mendelian, polygenic) traits.^1,2 It involves the inference of genetic and environmental effects from the comparison of the phenotypic correlation among monozygotic (MZ) and dizygotic (DZ) twins. A derived design is the discordant MZ (DMZ) twin design, which involves the study of MZ twins, who are phenotypically discordant. The discordancy may pertain to a binary disease status, ie, affected versus non-affected status, or to a metric phenotype, such as birth weight or intelligence. The DMZ design is a case-control design, with closer than usual matching between cases and controls, as the MZ twins are clones, and share many environmental influences, including prenatal environment. In contrast to the classical twin design, which is used to decompose phenotypic variance in genetic and environmental components, the DMZ design is used to identity unshared effects that may shed light on the causes or consequences of the MZ discordancy with respect to the phenotype of disease of interest.³

One might think that the advent of (increasingly cheaper) high-throughput genotyping technologies would have reduced the role of the twin design in the study of complex traits. In one sense this is indeed the case: the availability of large volumes of common genetic variants (GVs; notably, single nucleotide polymorphisms; SNPs) has enabled researches to go from estimating total genetic variance components using twins to estimate the variance explained by the measured SNPs,^4,5 and to identify the GVs contributing to the genetic variance in genome-wide association studies (GWAS).⁶ However, the twin design has remained relevant given the shift toward the study of genome-wide gene expression and its epigenetic regulation. The twin design has been used to determine the contributions of genetic and environmental influences to individual differences in gene expression⁷ and epigenetic marks, such as cytosine methylation, which are relevant to expression.⁸ The DMZ twin design, if anything, has gained relevance given the availability of measured (genome-wide) gene expression and epigenetic data.^9,10 Such data can be mined for causes or consequences of discordancy.^11,12 This extends the scope of unshared effects, the focus of the DMZ twin design, from the environmental to the genetic realm, including both structural differences affecting the DNA sequence (point mutations, de novo copy number variation (CNV) differences, and aneuploidy^13–15) and functional differences (gene expression and epigenetic marks). The presence of such differences emphasizes the fact that twins may be MZ, but are not necessarily genetically identical.¹⁶ Studies of whole genome sequencing in MZ pairs suggested that sequence-level differences are rare.^17,18 A recent review on de novo mutations concluded that post-zygotic de novo mutations are rare.¹⁹

Studies showing that complex-trait-associated variants identified through GWAS are largely enriched in regulatory regions of the genome suggest that variation in transcriptional control in relevant tissues plays a key role in individual differences in complex traits. The role of epigenetics and gene expression in complex phenotypes raises the question of how such effects should be represented in the twin model. The genetic effects in the twin model are based on the biometric model, which relates genotypes to a fixed genotypic effect and derives a polygenic effect from the summation of multiple fixed genetic effects.²⁰ Environmental effects are defined as effects not genetic, where shared effects account for any phenotypic resemblance exceeding that attributable to allele sharing, and unshared effects form a residual term of all non-genetic effects that cause differences between twins. As such, the twin model comprises little more than a fixed effects regression model in which a given phenotype is regressed on latent genetic and environmental variables. This model does not include an explicit account of how environmental effects impinge on the phenotype. Epigenetic processes are of interest in this regard, because internal and external environmental causes of methylation, for instance, provide a basis for an explicit account of how environmental factors may exert their influences.²¹ For instance, Castillo-Fernandez et al¹⁰ note that

use of epigenetic markers of environmental risk would greatly improve our understanding of the molecular basis of disease, as many complex traits have an environmental risk component that is often difficult to define and assess. Therefore, using epigenetic markers of environmental disease risk would help to identify environmentally driven disease mechanisms, including gene–environment interactions.

Given that epigenetic control of gene expression is a function of stochastic events, environmental effects (shared and unshared), and genetic effects,^8,22–24 what bearing does this have on the interpretation of the results of standard twin studies?

The aim of the present paper is to consider the implications of the results of recent genetic and epigenetic studies based on the DMZ design and the twin design. Specifically, we ask how we should represent epigenetic effects in the classical twin model, and what the implications are for the results obtained with the classical twin design. One interpretation of epigenetic effects on gene expression is that they form a third source of phenotypic variance, which in humans cannot be distinguished from unshared environmental effects.^25,26 An alternative interpretation, which takes into account the possibility that epigenetic effects may in part be under genetic control, is that they form a distinct source of variance besides the traditional genetic effects attributable to variation in the DNA sequence.^23,27 We present a conceptualization of epigenetic effects based on moderation of genetic effects. Specifically, we identify epigenetic effects as sources of interaction between the effect of genotype (DNA sequence variation) and any other effect (environmental, stochastic, and genetic), which gives rise to changes in the effects of the genotype on the phenotype by affecting gene expression.

The outline of this paper is as follows. We present the classical twin design briefly, outlining the fact that the twin model can be viewed as a fixed effects model. Subsequently, we review twin studies of methylation levels and discordant twin studies of the role of methylation in disease. As methylation is viewed as a source of variation in gene expression, we propose that variation in methylation levels may give rise to randomness in the genetic parameters in the twin model. We consider the consequences of ignoring this randomness in the twin design. Specifically, how does ignoring this randomness affect the results of a twin study?

The classical twin design

The classical twin design allows one to regress phenotypic scores (y) on a set of latent (unobserved) variables, so as to determine the proportion of phenotypic variance that is explained by the latent variables. In many twin studies, the latent variables comprise the additive polygenic variable (A), shared environmental (C), and unshared environmental variables (E), and the regression model is

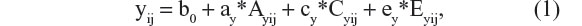
where y represents the phenotype of interest, subscript i denotes twin pair, subscript j denotes twin member within a pair, b₀ is the intercept, and a_y, c_y, and e_y are regression coefficients. As the variables A_y, C_y, and E_y are unobserved, we cannot observe their means and variances. This poses no problem, as we can impose a scale by standardization (zero mean and unit variance). Sometimes, a non-additive genetic factor, referred to genetic dominance (D_y), is modeled instead of C_y. This choice (D_y or C_y) is usually based on the inspection of the twin correlations. Whereas C_y increases the resemblance of both MZ and DZ pairs, D_y increases the resemblance of MZ pairs more than that of DZ pairs. The classical twin design is not possible to include both C_y and D_y as this model (including A_y and E_y) is not identified.^1,20,28 To ease presentation, we assume that D_y is absent. Assuming A_y, C_y, and E_y are uncorrelated, we have the following decomposition of the variance of the phenotype y:

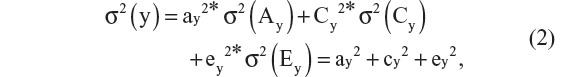
where the phenotypic variance, σ²(y), attributable to unshared environmental effects (E_y) may include (measurement) error variance. The heritability, denoted h_y², is the standardized genetic variance component, ie, h_y² = a_y²/(a_y² + c_y² + e_y²). This decomposition is identified in the twin design given the assumptions that the correlation between A_y of the first (A_y1) and second twin (A_y2) members of a twin pair, cor(A_y1,A_y2), equals one in MZ twins and one half in DZ twins. The latter is the expected proportion of alleles shared identically by descent in full sibs under the assumption of random mating.²⁹ The former follows from the working assumption that the MZ twins are genetically identical (but see Czyz et al^14,15). Furthermore, we have cor(C_y1,C_y2) = 1 and cor(E_y1,E_y2) = 0 by definition of shared and unshared environmental effects. That is, the shared environmental influences C contribute to similarity between members of a twin pair, while the unshared influences contribute to differences. We thus can express the twin covariances cov(y_i1y_i2) as 0.5*a_y²+c_y² in DZ twins and a_y²+c_y² in MZ twins, which along with Equation 2, allows us to estimate the parameters a_y, c_y, and e_y. This is typically done by means of genetic covariance structure modeling using maximum likelihood estimation.³⁰

In Equation 1, the phenotype y is assumed to be continuous. However, a binary phenotype, such as disease status, can be modeled in essentially the same way using the liability threshold model.³¹ In this model, we assume that the binary disease status is the manifestation of an underlying complex liability dimension (aka vulnerability). The liability is a continuous latent phenotype which is related to A_y, C_y, and E_y, as in Equation 1. Disease status depends on the liability in that a score on the liability beyond a given threshold value is associated with a diagnosis of being affected (eg, suffering major depression). The threshold value itself is a function of diagnostic criteria, and therefore possibly arbitrary. In the twin model of a binary variable, Equations 1 and 2 are applied to the bivariate liability, with the identifying constraint that the variance of the liability equals one (ie, a_y² + c_y² + e_y² = 1). This model is consistent with the view of disease etiology as a function of polygenic and environmental effects. It should be noted that relatively high liability heritability does not necessarily imply high concordance.³² For instance, given a liability h² of 0.80 and a disease prevalence of 1% (approximately the situation concerning schizophrenia), we expect to observe ~1.25% of the MZ twin pairs to be discordant, and the MZ proband-wise concordance rate to equal ~37.6 (DZ twin values are ~1.83% and ~8.66, respectively). The relatively low proband-wise concordance rate in combination with high heritability is consistent with the additive model given in Equations 1 and 2. Although low concordance is often interpreted as indicative of possible gene–environment interplay, a seemingly low proband concordance rate neither implies, nor rules out, such an interplay.

The DMZ design directly follows from the twin design. Any difference between MZ twins must be attributable to unshared effects (E_y), as genetic effects and shared environmental effects are a source of resemblance, not of difference. However, as noted above, unshared effects relevant to discordance may include genetic features.^14,15 In the case of a metric (continuous) phenotype, MZ phenotypic differences can be tested for association with differences in other variables by means of a regression model.³³ As explained in Gurrin et al³⁴ this model need not actually be limited to MZ twins, as the model can be extended to include DZ twins. In the case of a binary phenotype (eg, disease status), a logistic regression model or MacNemar’s test can be used.

The fixed effects in the twin model

We view the twin model (Equation 1) as a fixed effects model, in the sense that the regression parameters a_y, c_y, and e_y are assumed to be invariant over individuals. This assumption pertains to the ideal situation, in which the model (Equations 1 and 2) holds with respect to all individuals in the population of interest (in statistical terms, this implies that the data are identically and independently distributed³⁵). This fixed effects aspect of the model extends to the biometric model underlying the polygenic variable A, as this is the summation of individual effects of many GVs. In this model, each genotype at a given locus is assigned a genotypic effect. For example, in the case of a diallelic locus k (alleles B_k, b_k), the effects are μ_k + β_k (B_kB_k), μ_k + δ_k (B_kb_k) and μ_k − β_k (b_kb_k), where μ_k is the midparent value, β_k is the homozygote effect, and δ_k is the dominance deviation, which we assume to be zero here. Here, the effect β_k, which equals the regression coefficient in the regression of y_k on locus k (where B_kB_k, B_kb_k, and b_kb_k are coded −1, 0, and 1, respectively), is invariant over individuals, but β_k (k=1 … K) is variable over the K loci relevant to the phenotype.

The possibility that the regression parameters in the twin model may differ as a function of a covariate is generally recognized. For instance, the twin model can be extended to include opposite-sex DZ twin pairs, alongside male and female MZ and DZ twins.¹ This extended model can be used to test the (arguably epigenetic) hypothesis that a_y varies over sex, ie, the effect of genes on the phenotype of interest varies with sex, giving rise to a sex by genotype interaction. The presence of DZ opposite-sex twins allows for the additional test of the hypothesis that sex differences in the parameter a_y originate in the effects of different genes in males and females, or in the sex moderation of the effects of a single set of genes.¹ Purcell³⁶ and Zheng and Rathouz³⁷ presented a general moderation model, in which the genetic and environmental effects on a given measured phenotype (say, depression) may be moderated by an environmental phenotype (say, marital status), while taking into account the possibility that the latter may itself be subject to genetic effects. Although it is standard fare to test the hypothesis that the parameters in the twin model vary with respect to a well defined and measured covariate, we conceptualize epigenetic effects on the parameter a_y due to a latent (individual level) index of epigenetic influences.

Epigenetics: cytosine methylation

The modern definition of epigenetics emphasizes the regulation of gene expression that can be transmitted mitotically independent of DNA sequence. For instance, Tan³³ states: “In a broad sense, the epigenetic control over gene activity involves multiple molecular mechanisms (…), all of which act as ‘volume controls’ that up- or down regulate a gene’s expression without changing its DNA sequence”. These molecular mechanisms, which include histone modifications, DNA methylation, and non-coding RNAs,³⁸ are key mechanisms in establishing tissue identity.³⁹ Most studies of epigenetics in humans have focused on cytosine methylation, which occurs mainly at cytosines in cytosine–phosphate–guanine (CpG) dinucleotides. The effect of methylation on expression is position dependent: gene body CpG methylation is associated with transcriptional activity, while CpG methylation at promoter regions generally represses this activity.⁴⁰ The expression level of genes may be particularly related to the methylation level of their enhancers.⁴¹ Methylation results in changes in gene expression, which are mitotically heritable, but potentially reversible. While most CpGs are methylated,⁴² unmethylated CpGs may occur in clusters called CpG islands, which are present in the 5-prime regulatory regions of approximately 70% of human genes. Finally, methylation plays an important role in the silencing of repetitive elements such as transposons.⁴³ Individual differences in cytosine methylation are well established in clinical studies and twin studies. One source of individual differences in cytosine methylation is defects in imprinting, where normally the allele originating from one parent is silenced by means of methylation. A second source is epimutations, giving rise to variation in cytosine methylation, which may be due to stochastic errors (during mitosis), environmental, and genetic factors. Genetic factors associated with individual epigenetic differences that have been identified thus far include SNPs (ie, methylation quantitative trait locus,^44,45 Bell et al⁴⁶) and structural variation.^47,48

The classical twin design and the DMZ design are recognized as a useful tools in epigenetic studies.^{3,11,23,27,49,50} The DMZ design allows for the assessment of the disease association with differences in methylation, which is not confounded by genomic sequence variation. We note that post-zygotic mutations may undermine this design, as these introduce sequence variation between MZ twins at the loci of the mutations. Dal et al⁵¹ estimated that 5%–25% of the de novo mutations were post-zygotic in a healthy MZ twin pair, where the overall de novo mutation rate is 0.82–1.70×10⁻⁸ per base pair per generation (in the twins, this was 1.31×10⁻⁸ and 1.01×10⁻⁸). Acuna-Hildago et al⁵² estimated that each individual carries 2–7 post-zygotic de novo mutations. Zwijnenburg et al,¹² Bell and Saffery,²³ Czyz et al,¹⁴ Castillo-Fernandez et al,¹⁰ Tan,³³ and Tan et al⁴⁹ presented reviews of the results of genome wide and candidate gene (or region) epigenetic studies of DMZ twins. These studies concern a wide variety of medical disorders (eg, multiple sclerosis, asthma, Alzheimer’s disease, breast cancer, systematic lupus erythematosus, type I diabetes, and psoriasis), psychiatric disorders (schizophrenia, major depressive disorder, bipolar disorder, and autism spectrum disorders), psychological traits (ADHD [attention deficit hyperactivity disorder], risk-taking, and antisocial behavior), and physical traits (birth weight and Body Mass Index). Although these studies vary greatly in the scope and method of assay, tissue sample, statistical methods, and sample size, virtually all demonstrated (and often replicated; Castillo-Fernandez et al¹⁰) epigenetic differences relating to methylation.

Czyz et al,¹⁴ Bell and Saffery,²³ and Bell and Spector²⁷ reviewed the twin studies of methylation, based on either the classical twin design, or on MZ twins only. The aim of these studies is to establish whether genetic factors (DNA sequence variation) contribute to individual differences in methylation levels. A well-established finding is the increase with age of MZ epigenetic discordance, which may reflect the accumulation of epimutations due to stochastic errors and environmental influences.⁵³ This has been demonstrated cross-sectionally and longitudinally.⁵⁴ Chorionicity is implicated as mono-chorionic MZ twins are more discordant than dichorionic MZ twins⁵⁵ (Saffery et al),⁵⁶ which suggest that late twining is a factor. Heritability of methylation level is both tissue dependent and genomic region dependent.^55,57

van Dongen et al²² conducted a genome wide study of methylation based on buccal cells in ten 8–19-year-old MZ twin pairs. The overall average MZ correlation was 0.54 at CpG displaying high variability. The correlation varied as a function of region with higher correlations at CpG located in CpG islands, and lower correlations (ie, a greater role of unshared effects, including stochastic errors) in CpG poor regions. Bell et al²³ reported a genome-wide average h² of 0.18, based on an adult twin (30−80 years) study of DNA methylation in blood in 137 females twin pairs. A drawback of the twin design in this context is that the MZ correlation may vary due to intrauterine factors²⁴ and epigenetic starting point in the zygotic stage.²¹ McRae et al⁸ studied genome-wide methylation measures in peripheral blood lymphocytes, in an extended twin design, including adolescent twins, their siblings, and parents (614 individuals in 117 families). This design is appreciably less dependent on MZ data as it involves many additional relationships. McRae et al reported an average h² of 0.20, with ~65% of the 417,069 probes displaying h² greater than zero.⁸ Shared environmental influences explained very little variation in methylation levels.

In summary, epigenetic individual differences, pertaining to cytosine methylation, are largely attributable to unshared factors (unshared environmental effects and stochastic errors), and to a lesser extent to genetic factors. The relative contributions of genetic and environmental factors to variance vary with age, tissue and (genomic) region. The study of MZ twins discordant for disease has demonstrated the role of epigenetics in disease etiology.

Epigenetics as a source of random effects

As mentioned earlier, the twin design essentially allows us to carry out a regression analysis with the phenotype of interest (say, intelligence) as the dependent variable and the unmeasured genetic and environmental variables as independent variables. Supposing that we knew that individual differences in methylation were relevant to this phenotype, how should we represent these effects in the twin model, and, if ignored, what effect would they have on the decomposition of variance? The literature includes several different representations. Epigenetics has been viewed as a third source of variance, distinct from genetic and environmental sources. Given that this third source of variance is indistinguishable from unshared effects, it is supposed to increase the unshared environmental variance in the twin model.^25,26 This third source view was inspired by Gartner’s famous experiments, which demonstrated that isogenic organisms raised in homogeneous environmental circumstances display appreciable phenotype variance, presumably due to epigenetic effects stemming from stochastic errors.⁵⁸ Czyz et al¹⁴ questioned this interpretation for the following reason:

(…) the concept of stochastic epimutations as the third source of variation in opposition to genetic and environmental effects has important limitations because it is not evident that the random faults in methylation maintenance are not themselves genetically determined (…), or of environmental origin.

This does not detract necessarily from the third source interpretation in isogenic organisms in homogenous or enriched environments.⁵⁹ However, it seems unlikely that the representation in terms of a third source of variance mimicking unshared environmental effects is accurate in outbred human populations. In outbred populations, we have to incorporate epigenetic effects within the effects of DNA sequence differences and environmental differences.

Bell and Spector²⁷ and Bell and Saffery²³ represent DNA methylation effects explicitly as an independent source in the twin model, ie, a latent variable denoted M along side the latent variables A_y, C_y, and E_y. The twin correlation with respect to M may vary depending on age, tissue, etc. However, as the correlation is not generally zero, the M cannot be accommodated as a component of E_y. This representation acknowledges the fact that shared environmental factors (eg, chorionicity and age) and shared genetic factors may contribute to epigenetic individual differences. However, in our view the representation of epigenetic effects as a distinct source of variance does not sit well with the role of epigenetics as pertaining to gene expression regulation. That is, this representation assigns epigenetics the role of a main effect on the phenotype, alongside A_y, C_y, and E_y. But cytosine methylation is an effect on the expression of DNA sequence, and as such a source of moderation of genetic effects. We consider such moderation to be interpretable as an interaction between the genetic effects (originating in DNA sequence variation) and the causes (genetic, stochastic, and environmental) of epigenetic effects.

As explained earlier, in the standard twin model, we consider the parameter a_y as a fixed parameter, ie, not varying between members of the population of interest.³⁵ Now, given that methylation influences gene expression,^60,61 and expression influences genetic effect, we propose that the locus of the epigenetic effects is the parameter a_y, ie, the effects of DNA sequence variation at loci relevant to the phenotype y. In terms of the regression model, this implies that the parameter a_y is not fixed, but varies over individuals as a function of epigenetic individual differences at the loci relevant to the phenotype y. Simplifying the model by discarding shared environmental effects, we have

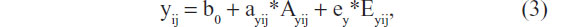
where a_yij is a random parameter, as indicated by the subject subscripts (as above: i for twin pair and j for member of a twin pair). This parameter is now effectively a (latent) phenotype subject to its own decomposition:

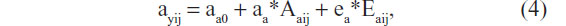
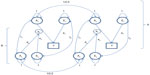
where a_yij is moderated by the genetic variable A_a (ie, genes influences methylation levels) and (external and internal) environmental variable E_a, which includes stochastic errors. The model is shown in Figure 1. Note that we allow A_y and A_a to be correlated (parameter r_A), and we allow E_y and E_a to be correlated (r_E). However, the genetic variables (A_a and A_y) are uncorrelated with the environmental variables (E_a and E_y), excluding any kind of genotype–environment covariance. The effect of A_a and E_a on the parameter a_y may be mediated by epigenetic marks such as methylation, which in turn influences expression levels.⁶¹ The exact causal chain from A_a and E_a to a_y is important, but beyond our primary question. That is, assuming the parameter a_y is actually random due to individual differences in epigenetic and environmental processes and outcomes, how will such randomness affect the results of a standard twin model, where a_y is treated as fixed? We address this issue by means of a small simulation study.

Figure 1 Twin model with random effects on the parameter ay. Part A is the standard twin model with unshared (Ey) and additive genetic (Ay) effects on the phenotype y; part B represents Aa and Ea as sources of randomness in the parameter ay (attributable to epigenetic effects). The parameter ay is encircled to indicate that it is a random (latent) variable.

The consequences of ignoring random effects in the twin model

The model in Figure 1 reduces to the standard twin model if a_y is a fixed value, ie, if the parameters a_a and e_a are zero. In that case, the additive genetic, unshared environmental effects (AE) model will fit the twin data well, and the h², equaling a_y²/(e_y² + a_y²), will accurately reflect the proportion of phenotypic variance attributable to additive genetic effects. By introducing the random effects by specifying non-zero a_a and e_a, we ask: how do such effects, if ignored in the twin model, affect the 1) phenotypic variance, 2) the twin correlations, 3) the estimate of h², and 4) the overall goodness of fit of the AE model. To this end, we carried out a small simulation study in which we simulated data according to Figure 1, with the parameter a_y random. We then fitted the standard twin model (a_y a fixed parameter; ie, ignoring the randomness) to determine the effects of the randomness on the results.

We set mean (a_y)=√0.5 and e_y=√0.5, and we set σ²(a_y) =0.025, 0.05, 0.075, and 0.1. Note that randomness in a_y implies randomness in the h² of the phenotype y (Figure 1). Given these settings, the mean h² is 0.5 and the standard deviation in h² is approximately 0.11, 0.15, 0.18, and 0.20 (corresponding to σ²(a_y) =0.025, 0.05, 0.075, and 0.1, respectively). We define h² as the proportion of phenotypic variance due to genetic factors in a population of individual who share the approximately same methylation levels. The h² of a_y was chosen to equal 0.2. This relatively low value is inspired by the fact that the genetic contributions to phenotypic variance in methylation levels are small.^8,23 We set the values of r_A and r_E to equal −0.3, 0, or 0.3. We suppose that these correlations could assume a non-zero value if the environmental (E_y) or genetic effects (A_y) on phenotype y also have a direct or an indirect effect on methylation. In addition, the genetic correlation may be due to linkage disequilibrium. The simulation results were obtained in analyses of 25,000 MZ and 25,000 DZ pairs. This large sample size ensures precise parameter estimates, and very great power to detect model misfit in terms of the likelihood ratio test (χ²(4)) of the standard AE twin model. This is the test of the AE model versus the saturated model, in which the MZ and DZ covariance matrices are estimated freely (ie, two-parameter model vs six-parameter model; hence, a 4 df test). We simulated the data in R,⁶² and fitted the AE model by means of maximum likelihood estimation using the OpenMx library in R.⁶³ The R script used in this simulation is available on request. This design gives rise to 36 parameter configurations (3 values of r_E, 3 values of r_A, 4 values of σ²(a_y)). We limit our discussion to the 18 parameter configurations shown in Table 1 (other results are available on request) with σ²(a_y) equaling either 0.025 or 0.10. We include in the table the values of the correlation r_A and r_E (columns 1 and 2), the variance σ²(a_y) (column 3), the phenotypic variance (σ²_mz) and correlation of the MZs (r_mz) (columns 4 and 5) and DZs (σ²_mz and r_dz; columns 6 and 7), the estimate of the additive genetic and environmental variance components (A and E; columns 8 and 9), the estimate of h² based on A and E (column 10), the χ² goodness-of-fit index of the AE model (column 11), and the expected variance in h² (column 12), given the variance in a_y (shown in column 3).

Table 1 Results of simulation Notes: σ2(ay) (column 3) is the variance in the parameter ay, columns 4–7 contain the summary twin statistics as observed in the data (phenotypic variance and phenotypic correlation), columns 9 and 10 contain the estimate of the genetic variance (A) and the environmental variance (E) based on the standard AE twin model, h2 is the heritability based on these estimates, column 11 contains the goodness-of-fit index of the standard AE model (the critical value given α=0.01 is 13.28). Column 12 shows the standard deviation of the h2 (σ(h2)), attributable to the variance in ay (column 3). The results were obtained in the analysis of 25,000 MZ and 25,000 DZ twin pairs. Abbreviations: AE, additive genetic, unshared environmental effects; DZ, dizygotic; MZ, monozygotic.

The third row in Table 1 shows the expected values of the parameters given σ²(a_y) =0. The values in the subsequent row show the observed values given σ²(a_y) =0.025 or σ²(a_y) =0.10. Note that in generating the data, σ²(a_y) is 0.025 or 0.10, but the results in columns 8–11 were obtained by fitting the standard AE twin model, in which a_y is not a random parameter. The χ² goodness of fit of the model increases with increasing σ²(a_y), ie, meaning that the model fit is poorer as σ²(a_y) increases. However, given σ²(a_y)=0.025 the effect on the χ² is negligible (Table 1, column 11). Given σ²(a_y) =0.1, the effect is evident, given the expected value of the likelihood ratio of 4. However, as the sample size is large (50,000), we consider the increase in the χ² to be minor (given α=0.01, the critical value is 13.28). The phenotypic variance increases from 1 (σ²(a_y) =0.0) to approximately 1.1 (σ²(a_y) =0.1). The estimates of the twin correlation are slightly lower than expected (ie, 0.5 and 0.25): the MZ correlations vary between 0.468 and 0.494, and the DZ correlation varies between 0.226 and 0.253. As a consequence, the estimate of the heritability is slightly lower than 0.5 (0.470–0.491). The values of r_A and r_E appear to have little effect on the results. We note that the effects of randomness in a_y are visible given σ²(a_y) =0.1, but overall fairly minor. The results in Table 1 were obtained with h² of a_y set to equal 0.2. We also considered a value of 0.5, but the results were comparable to those shown in the table (additional results available on request). We return to the implications of these results in the discussion.

Discussion

The aim of this paper was to consider the classical twin model in the light of epigenetic studies of methylation. Given that methylation is a source of variation in gene expression, we represented this in the twin model as randomness in the genetic regression parameter (parameter a_y in Equation 1; see also Figure 1). The model is simplistic as it represents only a snapshot of a process that may involve feedback from phenotype to the environment,⁶⁴ which in turn may influence methylation and gene expression. Yet, this representation is consistent with the biological view of methylation as a source of interaction, and with the definition of interaction in biometrical genetic modeling (ie, as a source of heteroskedasticity).^28,65 That is, methylation is represented as a cause of variation (ie, randomness) in the effects that genes have on the phenotype of interest. This representation has the advantage that it informs a twin model (Figure 1), which we used in a simulation study to assess the effects of ignoring such randomness. We assumed randomness in the genetic expression at many loci, gives rise to randomness in the sum of the effects at these loci, ie, the polygenic variable A_y. However, we did not assume that each locus contributing to A_y is necessarily subject to the effects of methylation.

On the basis of our small simulation study, we conclude that randomness in a_y has discernible, but small, effects on the results of the classical twin model (in which we ignore this randomness). Specifically, the results reflect quite accurately the role of E_y in terms of the parameter e_y, and the role of A_y in terms of the mean value of a_y in a well-fitting model. So assuming randomness in the parameter a_y, the twin model will reflect quite accurately the average genetic effect in terms of the h². The absence of appreciable misfit in terms of the likelihood ratio test implies that this test is “blind” to the misspecification of treating the random parameter a_y as fixed. Thus, the twin model produces a good estimate of the average h², but sheds no light on the possible standard deviation of h² arising from epigenetic effects. The variation in the h² was considerable: the values of given σ²(a_y)=0.1 implies that standard deviation of the h² was 0.20. We conclude that sensible results obtained in a well-fitting twin model cannot be taken to mean that the assumption that the genetic parameter is fixed (as mentioned earlier) is correct. Related to this is the fact that the twin model cannot detect genetic heterogeneity, ie, the possibility that a disease have several distinct genetic causes,⁶⁶ which are hard to distinguish phenotypically. For instance, the high heritability of schizophrenia (~0.80) neither implies nor rules out genetic heterogeneity.

Our results were based on quite arbitrary parameter settings and limited to an AE model. We tried other settings, which we considered reasonable, but obtain largely the same results. We included C effects on the phenotype, but these did not add anything to the results as we obtained the same results of good estimates of the effect of E and C, and good estimates of the average effects of A. We believe that the representation of epigenetic processes as a source parameter randomness (in a_y) in the twin model is plausible, and we are confident concerning the effects of such randomness (if ignored) on the results of standard twin modeling. However, we make no predictions concerning the ultimate importance of epigenetic mechanisms in twin studies in general – the importance is likely to depend in part on the phenotype. A version of the twin model that allows for the estimation of the variance in a_y would be useful to obtain an indication of the magnitude this effect. Such a model would definitely require additional information, such as repeated phenotypic measures, or (more demandingly) measures of methylation which are relevant to the phenotype of interest.

The classical twin design has been instrumental in demonstrating the role of genetic and environmental influences on a wide range of phenotypes. The accuracy of variance components obtained in twin studies depends on the validity of the many assumptions associated with this design.¹ While the twin model can be extended in various ways^2,67 to obtain more accurate estimates, the fact remains that these estimates answer the first in a sequence of questions. Immediate follow-up questions are which GVs contribute to polygenic components, and what is the nature of gene–environment interplay. These follow-up questions are currently being addressed thanks to the present means to measure genetic and epigenetic variables in large volumes. It is clear from many recent articles that the classical twin design and the DMZ design remains important tools in these studies.^{3,23,27,33,49} In this connection, it is interesting to note that the twin design, which has been criticized for providing no information on gene–environment interplay,⁶⁸ now is recognized to be an important tool in studying this interplay, at least insofar as it concerns epigenetics.

In conclusion, we have represented cytosine methylation as an epigenetic source of randomness in the genetic regression coefficient in the twin model. While we have emphasized methylation, we note that other epigenetic processes may moderate effects of DNA sequence variation (eg, DNA hydromethylation⁶⁹ and gene expression quantitative trait locus⁷). The actual source of moderation, or parameter randomness, is immaterial to the conclusions of our simulation. However, as we currently lack a model to evaluate this randomness in the twin model, we cannot say how important it is in terms of effect size. Possibly, the incorporation of methylation data in twin modeling along the lines of Purcell^36,37 may provide the means to quantify this randomness. It is interesting to note that such randomness, if appreciable, has implications for phenotypic modeling general. For instance, if two phenotypes are correlated due to pleiotropic genetic effects, and the effects are random (as defined in this paper), the phenotypic correlation will presumably also be random. The implications of epigenetic processes may therefore be of interest to other fields that focus on individual differences, such as psychology.

Acknowledgments

We gratefully acknowledge funding from the European Research Council (ERC-230374) Genetics of Mental Illness. JvD is supported by ACTION under the European Union Seventh Framework Program (FP7/2007-2013) under grant agreement no 602768. MN is supported by the Royal Netherlands Academy of Science (KNAW Academy Professor Prize PAH/6635). SvdS is financially supported by the Netherlands Scientific Organization (NWO/MaGW: VIDI-452-12-014).

Disclosure

The authors report no conflicts of interest in this work.

---

References

1.	Eaves LJ. Inferring the causes of human variation. J R Statist Soc Ser A. 1977;140(3):324–355.
2.	Eaves LJ, Last KA, Young PA, Martin NG. Model-fitting approaches to the analysis of human behaviour. Heredity. 1978;41(3):249–320.
3.	van Dongen J, Slagboom PE, Draisma HHM, Martin NG, Boomsma DI. The continuing value of twin studies in the omics era. Nat Rev Genet. 2012;3(9):640–653. doi:10.1038/nrg3243.
4.	Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 2011;88:76–82.
5.	So HC, Li M, Sham PC. Uncovering the total heritability explained by all true susceptibility variants in a genome-wide association study. Genet Epidemiol. 2011;35:447–456. doi:10.1002/gepi.20593.
6.	Neale BM, Ferreira MAR, Medland SE, Posthuma D. Statistical Genetics: Gene Mapping through Linkage and Association. London: Taylor and Francis; 2007.
7.	Wright FA, Sullivan PF, Brooks AI, et al. Heritability and genomics of gene expression in peripheral blood. Nat. Genet. 2014;46(5):430–437.
8.	McRae AF, Powell JE, Henders AK, et al (2014). Contribution of genetic variation to transgenerational inheritance of DNA methylation. Genome Biol. 2014;15:R73.
9.	Hogenson TL. Epigenetic as the underlying mechanism for monozygotic twin discordance. Med Epigenet. 2013;1:1–13.
10.	Castillo-Fernandez JE, Spector TD, Bell JT. Epigenetics of discordant monozygotic twins: implications for disease. Genome Med. 2014; 60(6):1–16.
11.	Boomsma D, Busjahn A, Peltonen L. Classical twin studies and beyond. Nat Rev Genet. 2002;3:872–882.
12.	Zwijnenburg PJG, Meijers-Heijboer HEJ, Boomsma DI. Identical but not the same: the value of discordant monozygotic twins in genetic research. Am J Med Genet Part B. 2010;153B:1134–1149.
13.	Gringras P, Chen W. Mechanisms for differences in monozygous twins. Early Hum Dev. 2001;64:105–117.
14.	Czyz W, Morahan JM, Ebers GC, Ramagopalan SV. Genetic, environmental and stochastic factors in monozygotic twin discordance with a focus on epigenetic differences. BMC Med. 2012;10:93. doi:10.1186/1741-7015-10-93.
15.	Czyz W, Ramagopalan SV. Molecular Genetic Causes of Discordance in Monozygotic Twins. In: eLS. Chichester: John Wiley & Sons. doi:10.1002/9780470015902.a0025033.
16.	Haque FN, Gottesman II, Wong AHC. Not really identical: epigenetic differences in monozygotic twins and implications for twin studies in psychiatry. Am J Med Genet Part C. 2009;151C:136–141.
17.	Ye K, Beekman M, Lameijer EW, et al. Aging as accelerated accumulation of somatic variants: whole-genome sequencing of centenarian and middle-aged monozygotic twin pairs. Twin Res Hum Genet. 2013;16:1026–1032.
18.	Weber-Lehmann J, Schilling E, Gradl G, Richter DC, Wiehler J, Rolf B. Finding the needle in the haystack: Differentiating “identical” twins in paternity testing and forensics by ultra-deep next generation sequencing. Genetics. 2014;9:42–46.
19.	Samuels ME, Friedman JM. Genetic mosaics and the germs line lineage. Genes. 2015;6:216–237. doi:10.3390/genes6020216.
20.	Falconer DS, Mackay TFC. Introduction to Quantitative Genetics. 4th ed. Harlow: Pearson Prentice Hall; 1996.
21.	Petronis A. Epigenetics as a unifying principle in the aetiology of complex traits and diseases. Nature. 2010;465(10):721–727. doi:10.1038/nature09230.
22.	van Dongen J, Ehli EA, Slieker RC, et al. Epigenetic variation in monozygotic twins: a genome-wide analysis of DNA methylation in buccal cells. Genes. 2014;5:347–365. doi:10.3390/genes5020347.
23.	Bell JT, Saffery R. The value of twins in epigenetic epidemiology. Int J Epidemiol. 2012;41:140–150. doi:10.1093/ije/dyr179.
24.	Gordon L, Joo JE, Powell JE, et al. Neonatal DNA methylation profile in human twins is specified by a complex interplay between intrauterine environmental and genetic factors, subject to tissue-specific influence. Genome Res. 2012;22(8):1395–1406. doi:10.1101/gr.136598.111.
25.	Molenaar PCM, Boomsma DI, Dolan CV. A third source of developmental differences. Behav Genet. 1993;23:519–524.
26.	Plomin R. Commentary: Why are children in the same family so different? Non-shared environment three decades later. Int J Epidemiol. 2011;40:582–592. doi:10.1093/ije/dyq144.
27.	Bell JT, Spector TD. A twin approach to unraveling epigenetics. Trends Genetics. 2011;27(3):116–125. doi:10.1016/j.tig.2010.12.005.
28.	Jinks JL, Fulker DW. Comparison of the biometrical genetical, MAVA, and classical approaches to the analysis of the human behavior. Psychol Bull. 1970;73(5):311–349.
29.	Visscher PM, Medland SE, Ferreira MAR, et al. Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genetics. 2006;2(3):e41. doi:10.1371/journal.pgen.0020041.
30.	Martin NG, Eaves LJ. The genetical analysis of covariance structure. Heredity. 1977;38(1):79–95.
31.	Falconer DS. The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann Hum Genet. 1965;29:51–76.
32.	Smith C. Heritability of liability and concordance in monozygous twins. Ann Hum Genet. 1970;34:85–91.
33.	Tan Q. Epigenetic epidemiology of complex diseases using twins. Med Epigenet. 2013;1:46–51. doi:10.1159/000354285.
34.	Gurrin LC, Carlin JB, Sterne JAC, Dite GS, Hopper JL. Using bivariate models to understand between- and within-cluster regression coefficients, with application to twin data. Biometrics. 2006;62:745–751. doi:10.1111/j.1541-0420.2006.00561.x.
35.	Molenaar PCM. On the limits of standard quantitative genetic modeling of inter-individual variation: extensions, ergodic conditions and a new genetic factor model of intra-individual variation. In: Hood KE, Halpern CT, Greenberg G, Lerner RM, editors. Handbook of Developmental Science, Behavior, and Genetics. Malden, MA: Blackwell; 2010:626–648.
36.	Purcell S. Variance components models for gene–environment interaction in twin analysis. Twin Res. 2002;5(06):554–571.
37.	Zheng H, Rathouz PJ. Fitting procedures for novel gene-by-measured environment interaction models in behavior genetic designs. Behav Genet. 2015;45:467–479.
38.	Goldberg AD, Allis CD, Bernstein E. Epigenetics: a landscape takes shape. Cell. 2007;128:635–638.
39.	Roadmap Epigenomics Consortium. Integrative analysis of 111 reference human epigenomes. Nature. 2015;518:317–330.
40.	Jones PA. Functions of DNA methylation: islands, start sites, gene bodies and beyond. Nat Rev Genet. 2012;13:484–492.
41.	Aran D, Sabato S, Hellman A. DNA methylation of distal regulatory sites characterizes dysregulation of cancer genes. Genome Biol. 2013;14:R21.
42.	Bird A. DNA methylation patterns and epigenetic memory. Genes Dev. 2002;16:6–21.
43.	Leonova KI, Brodsky L, Lipchick B, et al. P53 cooperates with DNA methylation and a suicidal interferon response to maintain epigenetic silencing of repeats and noncoding RNAs. Proc Natl Acad Sci. 2013;110:E89–E98.
44.	Banovich NE, Lan X, McVicker G, et al. Methylation QTLs are associated with coordinated changes in transcription factor binding, histone modifications, and gene expression levels. PLoS Genet. 2014; 10(9):e1004663. doi:10.1371/journal.pgen.1004663.
45.	Gibbs JR, van der Brug MP, Hernandez DG, et al. Abundant quantitative trait loci exist for DNA methylation and gene expression in human brain. PLoS Genet. 2010;6:e1000952. doi:10.1371/journal.pgen.1000952.
46.	Bell JT, Pai AA, Pickrell JK, et al. DNA methylation patterns associate with genetic and gene expression variation in HapMap cell lines. Genome Biology. 2011;12:R10.
47.	Colak D, Zaninovic N, Cohen MS, et al. Promoter-bound trinucleotide repeat mRNA drives epigenetic silencing in fragile X syndrome. Science. 2014;343(6174):1002–1005. doi:10.1126/science.1245831.
48.	Cabianca DS, Casa V, Bodega B, et al. A long ncRNA links copy number variation to a polycomb/trithorax epigenetic switch in FSHD muscular dystrophy. Cell. 2012;149(4):819–831. doi:10.1016/j.cell. 2012.03.035.
49.	Tan Q, Christiansen L, von Bornemann Hjelmborg J, Christensen K. Twin methodology in epigenetic studies. J Exp Biol. 2015;218:134–139. doi:10.1242/jeb.107151.
50.	Petronis A. Epigenetics and twins: three variations on the theme. Trends Genet. 2006;22(7):347–350.
51.	Dal GM, Ergüner B, Sagiroglu MS, et al. Early postzygotic mutations contribute to de novo variation in a healthy monozygotic twin pair. J Med Genetics. 2014;51:455–459.
52.	Acuna-Hidalgo R, Bo T, Kwint MP, et al. Post-zygotic point mutations are an underrecognized source of de novo genomic variation. Am J Hum Genetics. 2015;97:67–74.
53.	Fraga MF, Ballestar E, Paz MF, et al. Epigenetic differences arise during the lifetime of monozygotic twins. Proc Natl Acad Sci U S A. 2005;102:10604–10609.
54.	Talens RP, Christensen K, Putter H, et al. Epigenetic variation during the adult lifespan: cross-sectional and longitudinal data on monozygotic twin pairs. Aging Cell. 2012;11:694–703.
55.	Kaminsky ZA, Tang T, Wang AC, et al. DNA methylation profiles in monozygotic and dizygotic twins. Nat. Genet. 2009;41(2):240–245. doi:10.1038/ng.286.
56.	Saffery R, Morley R, Carlin JB, et al. Cohort profile: The peri/post-natal epigenetic twins study. Int J Epidemiol. 2012;41(1):55–61.
57.	Gervin K, Hammero M, Akselsen HE, et al. Extensive variation and low heritability of DNA methylation identified in a twin study. Genome Res. 2011;21:1813–1821.
58.	Gartner K. A third component causing random variability beside environment and genotype. A reason for the limited success of a 30 year long effort to standardize laboratory animals? Lab Anim. 1990;24:71–77.
59.	Freund J, Brandmaier AM, Lewejohann L, et al. Emergence of individuality in genetically identical mice. Science. 2013;340(6133):756–759. doi:10.1126/science.1235294.
60.	Schadt EE, Lamb J, Yang X, et al. An Integrative Genomics Approach to Infer Causal Associations between Gene Expression and Disease. Nat Genet. 2005;37(7):710–717. doi:10.1038/ng1589.
61.	van Eijk KR, de Jong S, Boks MPM, et al. Genetic analysis of DNA methylation and gene expression levels in whole blood of healthy human subjects. BMC Genomics. 2012;13:636. doi:10.1186/1471-2164-13-636.
62.	R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. Available from: http://www.R-project.org/. Accessed August 28, 2015.
63.	Boker S, Neale MC, Maes HH, et al. OpenMx: an open source extended structural equation modeling framework. Psychometrika. 2011;76(2):306–317.
64.	Dolan CV, de Kort JM, van Beijsterveldt CEM, Bartels M, Boomsma DI. GE covariance through phenotype to environment transmission: an assessment in longitudinal twin data and application to childhood anxiety. Behav Genetics. 2014;44(3):240–253. doi:10.1007/s10519-014-9659-5.
65.	Eaves LJ, Last K, Martin NG, Jinks JL. A progressive approach to non-additivity and genotype-environmental covariance in the analysis of human differences. Br J Math Statist Psychol. 1977;30:1–42.
66.	Wray NR, Maier R. Genetic basis of complex genetic disease: the contribution of disease heterogeneity to missing heritability. Curr Epidemiol Rep. 2014;2014(1):220–227.
67.	Keller MC, Medland SE, Duncan LE, et al. Modeling extended twin family data I: description of the cascade model. Twin Res Hum Genet. 2009;29:8–18.
68.	Dolan CV, Molenaar PCM. A note on the scope of developmental behaviour genetics. Int J Behav Dev. 1995;18:749–760.
69.	Wen L, Tang F. Genomic distribution and possible function of DNA hydroxymethylation in the brain. Genomics. 2014;104:341–346.