Back to Journals » Medical Devices: Evidence and Research » Volume 8
Machine learning and statistical methods for the prediction of maximal oxygen uptake: recent advances
Received 3 April 2015
Accepted for publication 20 July 2015
Published 27 August 2015 Volume 2015:8 Pages 369—379
DOI https://doi.org/10.2147/MDER.S57281
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 8
Editor who approved publication: Dr Scott Fraser
Fatih Abut, Mehmet Fatih Akay
Department of Computer Engineering, Çukurova University, Adana, Turkey
Abstract: Maximal oxygen uptake (VO2max) indicates how many milliliters of oxygen the body can consume in a state of intense exercise per minute. VO2max plays an important role in both sport and medical sciences for different purposes, such as indicating the endurance capacity of athletes or serving as a metric in estimating the disease risk of a person. In general, the direct measurement of VO2max provides the most accurate assessment of aerobic power. However, despite a high level of accuracy, practical limitations associated with the direct measurement of VO2max, such as the requirement of expensive and sophisticated laboratory equipment or trained staff, have led to the development of various regression models for predicting VO2max. Consequently, a lot of studies have been conducted in the last years to predict VO2max of various target audiences, ranging from soccer athletes, nonexpert swimmers, cross-country skiers to healthy-fit adults, teenagers, and children. Numerous prediction models have been developed using different sets of predictor variables and a variety of machine learning and statistical methods, including support vector machine, multilayer perceptron, general regression neural network, and multiple linear regression. The purpose of this study is to give a detailed overview about the data-driven modeling studies for the prediction of VO2max conducted in recent years and to compare the performance of various VO2max prediction models reported in related literature in terms of two well-known metrics, namely, multiple correlation coefficient (R) and standard error of estimate. The survey results reveal that with respect to regression methods used to develop prediction models, support vector machine, in general, shows better performance than other methods, whereas multiple linear regression exhibits the worst performance.
Keywords: machine learning methods, maximal oxygen consumption, prediction models, feature selection
Introduction
Maximal oxygen uptake (VO2max) refers to the maximal amount of oxygen that an individual can utilize during intense or maximal exercise. VO2max is expressed either as an absolute rate in liters of oxygen per minute (L min−1) or as a relative rate in milliliters of oxygen per kilogram of body mass per minute (mL kg−1 min−1). VO2max plays a significant role in both sport and medical sciences for different purposes. In sport sciences, it is often used as an indicator for endurance capacity of athletes, representing the upper limit of their aerobic fitness. Knowledge of VO2max can assist coaches in designing efficient training programs to maximize performance, minimize injury and fatigue of athletes, too.1,2 In medical sciences, it can serve as a metric to estimate the disease risk of a person, suggesting an unusually large amount of cholesterol, body fat, and blood pressure.3 Consequently, an accurate knowledge of VO2max has gained an increasing attention over the last decades.
The direct measurement of VO2max during a maximal graded exercise test (GXT) is accepted as the most accurate method for the assessment of aerobic power. However, despite a high level of accuracy, determining VO2max during maximal GXTs also entails a number of limitations. For example, conducting such tests require expensive and elaborated laboratory equipment, such as oxygen and carbon dioxide gas analyzers, an expiratory air flow probe, an air mixing chamber, a dehumidifier, a vacuum pump, and a data acquisition system. Trained staff is needed in order to perform the VO2max measurements and interpret the test results. In addition, maximal GXTs are unappealing to some individuals because the test requires exhausting exercise to the point of volitional exhaustion. Because of this, some older or higher risk individuals should not perform the test without medical supervision. Also, when the number of subjects is large, it is not feasible to apply VO2max tests for all subjects.4
The practical limitations of direct measurement have led to the development of various regression models for predicting VO2max that are principally based on one of the three different tests as follows: exercise tests, nonexercise tests, and hybrid tests.
Exercise tests in turn comprise maximal and submaximal tests. Maximal tests are expensive to administer and can be risky because the subject reaches the point of exhaustion in terms of heart rate (HR). The requirement of expensive gas analysis, ventilation equipment, and the need for medical attendance are the other major disadvantages of maximal tests.5 Because of these drawbacks of maximal tests, other methods that do not require maximal effort have been developed to determine VO2max. These methods use either submaximal exercise tests or nonexercise tests to predict VO2max.
Submaximal tests indirectly estimate VO2max using submaximal exercise variables and are usually performed on a treadmill, ergometer, or track. Submaximal tests have certain advantages over maximal tests, such as the specialized laboratory equipment is unnecessary, the test administrators require less training, and the exercise intensity is realistic for most participants. In addition, periodic submaximal testing provides a convenient way to monitor progress throughout an exercise program and educates participants about the selection of an appropriate intensity of exercise to develop individualized exercise programs. Submaximal tests are faster, safer, and cheaper to administer than maximal tests.
Nonexercise prediction equations enable an appropriate prediction of VO2max without the need to conduct a maximal or submaximal exercise test. Researchers may prefer nonexercise models instead of maximal and submaximal exercise tests due to their simplicity of administration to large populations, their independence from expensive laboratory equipment, and exercise testing. The main disadvantage of nonexercise tests is that they rely on the truthful self-report of activity and cannot be utilized when the individuals have an interest in the results, giving them a reason to falsify the self-reported activity levels.5–7
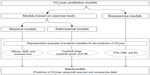
Representative examples for maximal variables include maximal heart rate (HRmax), rating of perceived exertion (RPE), and exercise time, whereas treadmill stage, treadmill speed, and exercise HR are popular examples for submaximal variables. On the other hand, questionnaire variables, such as perceived functional ability (PFA), physical activity rating (PAR), and activity code (AC), belong to the class of nonexercise variables. Figure 1 illustrates an overview of various types of VO2max prediction models along with their representative examples of predictor variables.
The purpose of this paper is to give a detailed overview about the data-driven modeling studies, such as linear regression models and artificial neural network models, for the prediction of VO2max conducted in recent years. Also, the performance and prediction accuracies of such various regression models reported in related literature are compared with each other in terms of multiple correlation coefficient (R) and standard error of estimate (SEE) in order to identify the best set of predictor variables along with the used machine learning and statistical methods. The R and SEE values are the most popular and frequently used metrics in the field of sport physiology, and also vast majority of the studies related to the prediction of VO2max use R and SEE for performance and accuracy evaluations of prediction models.
The rest of the paper is structured as follows. The “Prediction models based on exercise tests” section presents the prediction models based on exercise tests that have used either maximal or submaximal tests for the prediction of VO2max. The “Nonexercise prediction models” section introduces the nonexercise prediction models. The “Hybrid models” section gives details about the hybrid prediction models, which combine data obtained from both exercise and nonexercise tests. The “Overview of prediction methods and model evaluation techniques” section gives a brief overview of the machine learning and statistical methods as well as model evaluation techniques encountered within the scope of this study. Finally, the “Conclusion and future work” section concludes the paper and gives pointers to future work.
Prediction models based on exercise tests
Maximal prediction models
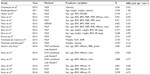
Chatterjee et al8 validated the relevance of the 20 m multistage shuttle run test (20 m MST) in Nepalese adult females. Forty female students, aged from 20 years to 24 years, from diverse colleges of Nepal were selected for the study. Direct estimation of VO2max included treadmill exercise followed by expired gas analysis by scholander microgas analyzer, whereas VO2max was indirectly predicted by the 20 m MST. Maximal shuttle run velocity was used to predict the VO2max with the help of multiple linear regression (MLR). The R and SEE values were reported to be 0.94 and 0.53 mL kg−1 min−1, respectively.
Bandyopadhyay9 examined the effectivity of 20 m MST for the prediction of VO2max in male university students using MLR. Eighty-four stationary male university students of the same socioeconomic background were selected from students of University of Calcutta, Kolkata, India, to test the efficiency of 20 m shuttle run test (SRT) for indirect estimation of VO2max. Predictor variables that are used to develop the linear regression model incorporate age, height, weight, and velocity. The R and SEE values were reported to be 0.94 and 1.38 mL kg−1 min−1, respectively.
Mahar et al10 created and cross-validated regression models to predict VO2max from progressive aerobic cardiovascular endurance run (PACER) 20 m shuttle run performance in 10–16-year-old boys and girls. PACER performance and VO2max were evaluated using a dataset composed of 244 participants. The dataset was randomly separated in validation (n=174) and cross-validation (n=70) samples. The validation sample was utilized to build the regression models for predicting VO2max from sex, age, body mass index (BMI), and PACER. Values of R and SEE for the best model were found as 0.75 and 6.17 mL kg−1 min−1, respectively.
Akay et al11 developed VO2max models by using different regression methods, such as support vector machine (SVM), multilayer perceptron (MLP), generalized regression neural network (GRNN), and MLR. The dataset included data of 439 subjects (211 males and 228 females) who are apparently healthy volunteers ranging in age from 20 years to 79 years. The predictor variables used to develop the models were sex, age, BMI, body fat percentage (BF%), respiratory exchange ratio (RER), RPE, HRmax, and time to exhaustion from treadmill test. For model testing, tenfold cross-validation has been conducted. The most accurate R and SEE values were obtained by MLP with 0.91 and 3.73 mL kg−1 min−1, respectively. In a follow-up study, Akay et al12 combined SVM and MLR methods with the Relief-F feature selection algorithm to identify the discriminative predictors of VO2max using the same dataset. The models included the predictor variables sex, age, BMI, HRmax, RPE, RER, and exercise time. According to the results obtained, the model made up of five predictor variables including sex, age, BMI, HRmax, and exercise time performed better than the model including the full set of predictor variables, independent of whether it was evaluated with SVM or MLR. SVM-based models, in turn, outperformed MLR-based models. The values of R and SEE for the most accurate SVM-based model were reported as 0.90 and 4.58 mL kg−1 min−1, respectively.
Silva et al13 developed and tested two models to predict VO2max in Portuguese youths, aged from 10 years to 18 years, using a 20 m SRT. Participants (60 males and 54 females) were divided into estimation and cross-validation groups, and their VO2max was directly measured by wearing a portable gas analyzer during the SRT. MLP and MLR methods were applied by using sex, age, height, weight, BMI, and SR stage as predictors of VO2max. The reported R and SEE values were 0.84 and 4.90 mL kg−1 min−1, respectively.
Daros et al14 developed a maximum aerobic power test and prediction equations to estimate VO2max for soccer athletes using MLR. The proposed test composed of applying progressive, persistent, and maximal speed running that covers 80 m, organized in a square (20 m ×20 m), where the athletes performed until they became exhausted. The dataset was made up of 24 young soccer players aged 16.66±1.49 years, each of them was a practitioner of the sport for at least 4 years. Two VO2max estimation equations were developed that incorporated total distance and maximum speed as predictor variables. The highest R and the lowest SEE were found as 0.76 and 4.29 mL kg−1 min−1, respectively.
Costa et al15 developed equations to predict the VO2max of nonexpert adult swimmers. Participants were 22 male nonexpert swimmers (aged between 18 years and 30 years). A progressive swim test was conducted, in which there occurs an increase in the intensity of the swim every two laps. Three different MLR-based equations were developed using the predictor variables, such as weight, number of laps performed, and after HR. According to the performances obtained by the three models, best values of R and SEE were determined as 0.80 and 7.20 mL kg−1 min−1, respectively.
Machado and Denadai16 presented a specific predictive equation to predict the VO2max from boys aged between 10 years and 16 years, with the help of MLR. Forty-two boys conducted a treadmill running ergospirometric test, with the introductory speed adjusted at 9 km h−1, until voluntary exhaustion. The predictor variables weight and velocity have been utilized to establish the prediction equation. R and SEE values of the equation were reported as 0.93 and 4.10 mL kg−1 min−1, respectively.
Aktürk and Akay17 employed MLP combined with Relief-F feature selection algorithm to develop VO2max prediction models for healthy subjects ranging in age from 18 years to 65 years. The dataset comprised 100 subjects (50 males and 50 females) and included the predictor variables, such as sex, age, BMI, HRmax, RPE, RER, and grade. For model testing, tenfold cross-validation was used. The results showed that the model, including six predictor variables (sex, age, BMI, HRmax, RER, and grade), yielded the highest R and the lowest SEE with 0.86 and 4.62 mL kg−1 min−1, respectively. The model including the full set of predictor variables, on the other hand, yielded the second highest R and lowest SEE with 0.86 and 4.65 mL kg−1 min−1, respectively.
Akay et al18 predicted VO2max of cross-country skiers using different regression methods, including SVM using the radial basis function, linear SVM and MLP. The dataset contained information pertaining to 175 cross-country skiers (101 males and 74 females) aged between 15 years and 30 years. Predictor variables that were used to build the models were sex, age, BMI, HRmax, HR at lactate threshold, exercise time, and protocol. Tenfold cross-validation was applied on the dataset. The values of R and SEE for the most accurate model were attained by SVM using the radial basis function with 0.83 and 4.39 mL kg−1 min−1, respectively.
Table 1 gives an overview of recent studies in literature that developed maximal models for the prediction of VO2max. The studies are sorted in chronological order. For each study, only the R and SEE values for the most accurate model along with its predictor variables are reported. For the case where more than one regression method is utilized in a study, the best values of R and SEE for a prediction model are reported for every regression method. The R values are the averages of cross-validation testing data, where cross-validation has been applied. In all other cases, R values belong to the testing data.
Submaximal prediction models
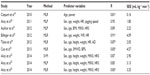
Coquart et al19 presented an indirect method for predicting VO2max from a submaximal GXT in obese women by using MLR. Thirty obese women performed maximal GXT to volitional exhaustion to determine the reference value for VO2max. During GXT, the power at RPE 15 was measured, too. The predictor variables, age and power at RPE 15 elicited during a submaximal GXT, were found to produce a reasonably accurate prediction of VO2max in obese women. The values of R and SEE were reported as 0.83 and 0.16 mL kg−1 min−1, respectively.
Akay et al20 developed an accurate MLP model to predict VO2max of fit adults from a single-stage submaximal treadmill jogging test. For the study, 126 participants (81 males and 45 females) aged from 17 years to 40 years successfully completed a maximal GXT to determine the VO2max. The variables, such as sex, age, weight, HR, and jogging speed, were used to build the MLP-prediction model. The highest R and the lowest SEE values were reported as 0.95 and 1.80 mL kg−1 min−1, respectively.
Açikkar et al21 built MLP models to predict VO2max from submaximal endurance exercise at varying distances (0.5 mile, 1.0 mile, and 1.5 mile), involving walking, jogging, or running. In total, 185 (115 males and 70 females) “apparently healthy” college students, aged 18–26 years, successfully completed a submaximal 1.5-mile endurance test and a maximal GXT. Predictor variables utilized to create the prediction models involved sex, age, BMI, the elapsed exercise times (MIN1, MIN2, and MIN3), and HRs (HR1, HR2, and HR3) at the 0.5 mile, 1 mile, and 1.5 mile distances, respectively. Using tenfold cross-validation on the dataset, values of R and SEE for the most accurate prediction model were reported as 0.89 and 2.22 mL kg−1 min−1, respectively. In a follow-up study, Akay et al22 developed various VO2max prediction models based on SVM using the same dataset. The predictor variables employed to build the models remained the same, with the exception of BMI, instead of which the height and weight variables have been utilized. For comparison purposes, VO2max prediction models based on MLP and MLR were also developed. In conclusion, it was observed that SVM-based models showed better performance than the ones obtained by using MLP and MLR-based prediction models. The values of R and SEE for the most accurate SVM-based model were reported as 0.87 and 2.90 mL kg−1 min−1, respectively.
Billinger et al23 inspected the capability of the Young Men’s Christian Association submaximal exercise test protocol using a total body recumbent stepper to predict VO2max. One-hundred and ten 18–60-year-olds were screened for the study by fulfilling the participation criteria of low-to-moderate cardiovascular disease risk. The subjects were requested to keep a pace of 100 stages every minute, and the resistance rose in 3 minutes intervals as specified by the protocol until the subjects became tired, or 85% of HRmax was attained. The predictor variables, sex, age, weight, HR, and work rate expressed in Watts, were utilized to form the MLR-based prediction model. A cross-validation study was conducted to validate the accuracy of the prediction equation. The presented R and SEE values were 0.92 and 4.09 mL kg−1 min−1, respectively.
Tönis et al24 determined parameters that can be utilized for predicting VO2max, from a combination of HR and accelerometer data. Data were obtained from 41 (23 males and 18 females) healthy subjects, ranging in age from 20 years to 29 years. The measurement protocol consisted of a submaximal single-stage treadmill walking test for VO2max estimation followed by a walking test at two different speeds (4 km h−1 and 5.5 km h−1) for parameter determination. MLR analysis was performed using general subject measures such as sex, age, height, weight, BMI, and intercept and slope of the relation between HR and accelerometer output during walking as independent variables to predict the VO2max. The R and SEE values were reported as 0.90 and 2.05 mL kg−1 min−1, respectively.
Cao et al25 built new VO2max prediction models using a perceptually regulated 3-minute walk distance (3MWD) test. VO2max was measured with a maximal incremental cycle test in 283 Japanese adults. A 3MWD test was performed at a self-regulated intensity corresponding to RPE 13. Three prediction models were developed by using MLR for predicting VO2max using data on sex, age, 3MWD, BMI, waist circumference, and BF%. The R and SEE values of the best model were reported as 0.84 and 4.57 mL kg−1 min−1, respectively.
Table 2 gives an overview of recent studies in literature that used submaximal models for the prediction of VO2max in chronological order.
Nonexercise prediction models
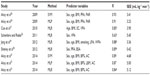
Akay et al26 developed nonexercise VO2max prediction models by using SVM and MLP. VO2max values of 100 subjects (50 males and 50 females) were measured by using a maximal GXT. The variables, such as sex, age, BMI, PFA and PAR, were used to build two nonexercise prediction models. The PFA question is designed to determine how fast participants believe they could walk, jog, or run one mile (PFA-1) and three mile (PFA-2) distance without becoming overly breathless or fatigued. The sum of the responses to the PFA-1 and PFA-2 questions is the PFA score. The PAR question allows participants to self-assess their level of PA within the last past 6 months. For model testing, tenfold cross-validation was utilized. It has been concluded that SVM-based nonexercise prediction models performed better than the MLP-based models and can be valid predictors of VO2max. The highest R and the lowest SEE values were obtained by the SVM-based model with 0.91 and 3.23 mL kg−1 min−1, respectively.
Cao et al27 examined the use of the accelerometer-determined PA variables as the objective PA variables for predicting VO2max in Japanese adult men. In total, 127 Japanese adult men aged from 20 years to 69 years were selected as subjects for the study. The nonexercise prediction models were developed and cross-validated with the help of MLR and using the predictor variables, such as age, BMI, step count, and vigorous PA (VPA). The reported values of R and SEE are 0.86 and 3.90 mL kg−1 min−1, respectively.
Schembre and Riebe28 established a VO2max estimation equation derived from the International Physical Activity Questionnaire (IPAQ)–Short Form. To conduct the regression analysis, 80 college-aged males and females completed the IPAQ–Short Form and completed a maximal exercise test. The estimation equation was created using MLR along with predictor variables sex and VPA. It has been shown that the IPAQ–Short Form can be used in successfully estimating VO2max. The most accurate values of R and SEE were reported as 0.65 and 5.45 mL kg−1 min−1, respectively.
Jang et al29 determined whether work-related PA (WPA) is a potential predictor of VO2max and developed a VO2max equation using a MLR-based nonexercise regression model for the cardiorespiratory fitness test in Korean adult workers. In total, 217 (113 males and 104 females) adult subjects aged from 21 years to 63 years were recruited for the study. Self-report questionnaire survey was conducted on study subjects, and VO2max of each subject was measured with the exercise test. The variables used for the prediction of VO2max include sex, age, BMI, smoking, leisure-time PA (LPA), and the factors representing WPA. In conclusion, the WPA was revealed to be a predictor of VO2max. The R and SEE values were presented as 0.89 and 3.36 mL kg−1 min−1, respectively.
Shenoy et al30 employed MLR to produce an equation-based model to predict treadmill VO2max scores based on nonexercise data. In this study, 120 college-aged participants (60 males and 60 females) voluntarily participated and successfully completed a maximal GXT on a motorized treadmill to assess VO2max. Relevant nonexercise data included PFA and PAR scores as well as the body surface area. The accuracy of the model was evaluated by conducting a cross-validation analysis. The presented R and SEE values were 0.90 and 0.42 mL kg−1 min−1, respectively.
Akay et al31 employed SVM to develop new nonexercise VO2max prediction models for healthy subjects ranging in age from 18 years to 65 years. The dataset included VO2max values of 126 subjects as well as the predictor variables such as age, sex, BMI, BF%, lean body mass, and finally, the questionnaire variable AC that describes the level of PA. In order to compare the performance of SVM-based VO2max prediction models, MLP and MLR prediction models were developed, too. Tenfold cross-validation was used on the dataset. The highest R and the lowest SEE values for the most accurate SVM-based model were presented as 0.89 and 4.68 mL kg−1 min−1, respectively.
A summary of recent studies that developed nonexercise models for the prediction of VO2max is presented in Table 3 in chronological order.
Hybrid models
Nielson et al32 built a MLR model for predicting treadmill VO2max scores using both exercise and nonexercise variables. For the study, 105 college-aged participants (53 males and 52 females) successfully accomplished a submaximal cycle ergometer test and a maximal GXT on a motorized treadmill. Relevant data incorporated weight, ending steady-state HR, ending work rate, PFA, and PAR. The values of R and SEE were reported as 0.91 and 3.36 mL kg−1 min−1, respectively.
Akay et al33 built a MLP model using submaximal and nonexercise variables to predict VO2max in healthy volunteers. The dataset included data of 100 subjects (50 males and 50 females) ranging in age from 18 years to 65 years. The predictor variables of the dataset were sex, age, BMI, PAR, HR, and treadmill stage, and tenfold cross-validation has been carried out on the dataset. The presented SEE and R values were 0.96 and 2.01 mL kg−1 min−1, respectively. In a follow-up work, Akay et al34 developed VO2max prediction models based on maximal and nonexercise variables, with the help of MLP and MLR using the same dataset. Predictor variables used to form the prediction models incorporated the physiological variables sex, age, and BMI; the maximal variables grade, RPE and HRmax; and finally the questionnaire variables PFA and PAR. The highest R and the lowest SEE values were reported for the MLP-based model with 0.94 and 2.28 mL kg−1 min−1, respectively.
Yücel et al35 investigated the effects of PFA-1, PFA-2, and PAR variables on the prediction of VO2max by using MLP and MLR. Rest of the predictor variables used to form the prediction models were the physiological variables, such as sex, age, and BMI, and the submaximal variables ending speed, HR, and stage of the exercise test. According to the results obtained, two conclusions were made. First, inclusion of PFA and PAR scores in VO2max models yielded 18.26%–28% and 17.92%–26.99% reductions in SEEs for MLR- and MLP-based models, respectively. Second, MLP-based models showed much better performance than MLR-based models. Among the results obtained by MLP-based models, the highest values for the R and SEE were found as 0.93 and 3.15 mL kg−1 min−1, respectively. A similar study on the same dataset was conducted by Akay et al,36 with the intention to examine the effects of the PFA-1, PFA2, and PAR variables on the prediction of VO2max using SVM. Predictor variables included the physiological variables sex, age, weight, and height; the submaximal variables ending speed and HR; and the three questionnaire variables PFA-1, PFA-2, and PAR. The inclusion of PFA and PAR scores in SVM-based VO2max models yielded an average of 8.9% and 10.51% reductions in SEEs for SVM- and MLR-based models, respectively. The values for the highest R and the lowest SEE were found as 0.93 and 3.25 mL kg−1 min−1, respectively.
Table 4 lists recent studies in literature that developed hybrid models for the prediction of VO2max in chronological order.
Overview of prediction methods and model evaluation techniques
Machine learning and statistical methods
SVM is considered as one of the most promising regression methods, which is widely utilized in many application areas due to its high prediction accuracy. Although SVMs were initially designed to solve classification problems, they have been lately reconstructed to also cope up with regression problems. In order to perform a regression analysis, SVM constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space. The effectiveness of SVM-based models depends on the selection of the kernel function, the kernel function’s parameters, and the regularization parameter C. A common choice is the radial basis function kernel, which has a single-optimization parameter gamma (γ). The optimal values of C and γ are often chosen by a grid search method.37
MLP belongs to the class of feed-forward artificial neural networks that can map sets of input data onto a set of convenient outputs. The basic constituents of a MLP are the neurons, which imitate the processing of human brain neurons. The neurons are organized into layers, and in any two contiguous layers, the neurons are linked in pairs with weighted edges. A practical MLP network possesses one input layer, one or more hidden layers, and one output layer. Usually, the back propagation algorithm is employed for training this network. The activation functions of the hidden and output layers, the number of neurons in the hidden layer, the number of epochs, the learning rate, and the momentum determine the performance of MLP-based models.38
GRNN falls into the category of probabilistic neural networks and does not necessitate an iterative training procedure as back propagation networks. It approximates any arbitrary function between input and output vectors, drawing the function estimate directly from the training data. A GRNN has four layers, which are input layer, pattern layer, summation layer, and output layer. Minimum and maximum values for sigma, search step, and the type of kernel function influences the performance of GRNN-based models.39
Finally, MLR is almost a standard technique frequently used in sport physiology to investigate the linear relationships between one or more predictor variables and a single-target variable. The case of regression analysis with one predictor variable is also called as simple linear regression. MLR can be considered as an extension of simple linear regression in such a way that it can use two or more predictor variables in an equation to predict a desired target variable.
Model validation and testing techniques
Both model validation and testing evaluate a model’s performance, with the difference that they are applied at different stages of a model’s lifetime. Validation is performed to evaluate the goodness of fit of a learned model, which in turn reflects the quality and performance of hyperparameters optimized for a learning algorithm during model training. Validation of a prediction model is carried out prior to real testing or deployment. Once the prediction model is trained and deployed, it can be continued with the stage of model testing, where the performance of a validated model is evaluated on a test dataset. This kind of testing does not necessitate retraining the model. For validation and testing purposes, one and the same dataset can be used as long as the test set does not contain the validation set.
For model validation and testing, there exists in principle two techniques, which are referred to as hold-out validation and cross-validation. Hold-out validation is straightforward in concept, and the dataset is partitioned into two disjoint training and testing sets. A prediction model is trained using the training set only. Then, the trained model is evaluated against the previously unseen data in the testing set to predict the desired target values. Normally, less than one-third of the initial dataset is utilized for the validation of data. The advantage of the hold-out validation is that it is executed on independent training and test sets, which may increase the reliability of model validation and testing, also it takes no longer to compute. However, its evaluation can have a high variance. The performance of this technique may rely heavily on the fact at which point the separation between training and test set is carried out. Another drawback refers to the fact that the number of training examples is reduced due to the strict separation of the original dataset in training and test sets. Cross-validation, as being the alternative to hold-out validation, is utilized in practice with the expectation of being more accurate than the hold-out estimate without reducing the number of training examples within a dataset. Although there exist many variants of cross-validation, the most commonly known variant is k-fold cross-validation. The k-fold procedure partitions the data into k equally sized folds. For a given a hyperparameter setting, every k-fold is handled similar to a hold-out set. The model is trained on the remaining k-1 folds, and its quality and performance are validated on the held-out fold. This principle is reiterated for each fold, and the overall performance is calculated as the average of the performance on all k-folds. In data mining and machine learning, tenfold cross-validation (k=10) is the most common variant. If k equals the sample size, this is called leave-one-out cross-validation. Cross-validation is especially useful when the dataset comprises a limited number of entries and cannot be reduced at the expense of validation purposes.
Conclusion and future work
This study presented an overview about the data-driven modeling studies for the prediction of VO2max conducted in recent years. Numerous models have been presented to predict VO2max of various target audiences, ranging from soccer athletes, nonexpert swimmers, cross-country skiers to healthy fit adults, teenagers, and children using various machine learning and statistical methods and different sets of predictor variables. Representative examples of variables for the prediction of VO2max range from physiological variables, such as sex, age, weight, height, and BMI, to maximal or submaximal exercise variables, such as HRmax, RPE, treadmill stage, and treadmill speed, to nonexercise variables, including PFA, PAR, and AC. The performance of the presented prediction models has been compared with respect to their achieved R and SEE values.
Considering the survey results obtained, several conclusions can be reached. First of all, at the beginning of research efforts for the prediction of VO2max, almost all of the studies used MLR for developing various VO2max prediction equations. However, with the employment of intelligent data processing techniques, such as SVM and MLP, it has been shown that VO2max prediction models based on these techniques led to higher Rs and lower SEEs than MLR-based prediction models. In more detail, SVM-based models, in general, have shown better performance than other regression methods for the prediction of VO2max. In contrast, MLR-based models, in general, have yielded the lowest Rs and the highest SEEs, suggesting that VO2max has nonlinear characteristics.
Second, when all prediction models presented in this study are investigated, it is observed that, on average, submaximal exercise-based models perform better than nonexercise-based models, whereas nonexercise-based models, in turn, outperform maximal exercise-based models for the prediction of VO2max. Hybrid models, on the other hand, that combine nonexercise-based models, with maximal- or submaximal-based models, have the potential to improve the accuracy of VO2max prediction over single models.
Third, feature selection algorithms have been applied on different datasets to reveal the relevant and irrelevant features for the prediction of VO2max. The results show that using the full set of predictor variables does not always lead to most accurate results. In contrast, it has been reported that VO2max can be predicted with higher Rs and lower SEEs using lesser number of predictor variables.
Fourth, the physiological variables, such as sex, age, height, weight, and BMI, in general, have been found to be the most important variables in building accurate prediction models, and they accordingly appear in almost each model giving predictions within acceptable limits of accuracy.
Future work can be performed in a number of different areas. Other promising regression methods as proposed in studies of Evrendilek and Karakaya40,41 can be utilized that have never been applied for the development of VO2max prediction models. Different further feature selection algorithms such as minimum redundancy maximum relevance42 and correlation-based feature selection43 can be combined with these regression methods to identify the discriminative features for the prediction of VO2max.
Also, ensemble methods can be utilized in developing new VO2max models that combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability and robustness over a single estimator.
Disclosure
The authors report no conflicts of interest in this study.
References
Davis JM, Carlstedt CJ, Chen S, Carmichael MD, Murphy EA. The dietary flavonoid quercetin increases VO2max and endurance capacity. Int J Sport Nutr Exerc Metab. 2010;20(1):56–62. | |
Karahan M. The effect of skill-based maximal intensity interval training on aerobic and anaerobic performance of female futsal players. Biol Sport. 2012;29(3):223–227. | |
Liberato SC, Maple-Brown L, Bressan J, Hills AP. The relationships between body composition and cardiovascular risk factors in young Australian men. Nutr J. 2013;12:108. | |
Karp J. The three players of distance running: an in-depth look at running economy. Track Coach. 2008;180:5737–5742. | |
Hunn HM, Lapuma PT, Holt DT. The influence of pre-test anxiety, personality and exercise on VO2max estimation. J Exerc Physiol. 2002;5(1):5–14. | |
Chatterjee S, Chatterjee P, Bandyopadhyay A. Prediction of maximal oxygen consumption from body mass, height and body surface area in young sedentary subjects. Indian J Physiol Pharmacol. 2006;50(2):181–186. | |
McComb R, Jacalyn J, Roh D, Williams JS. Explanatory variance in maximal oxygen uptake. J Sports Sci Med. 2006;5(2):296–303. | |
Chatterjee P, Banerjee AK, Das P, Debnath P. A regression equation for the estimation of maximum oxygen uptake in Nepalese adult females. Asian J Sports Med. 2010;1(1):41–45. | |
Bandyopadhyay A. Validity of 20 meter multi-stage shuttle run test for estimation of maximum oxygen uptake in male university students. Indian J Physiol Pharmacol. 2011;55(3):221–226. | |
Mahar MT, Guerieri AM, Hanna MS, Kemble CD. Estimation of aerobic fitness from 20-m multistage shuttle run test performance. Am J Prev Med. 2011;41(4):117123. | |
Akay MF, Ghahremanlou NS, Aktürk E, George JD, Aktarla E. Performance comparison of different regression methods for VO2max prediction. In: 7th International Symposium on Electrical and Electronics Engineering and Computer Systems. Lefka, North Cyprus; European University of Lefke. 2012:7–11. | |
Akay MF, Akgöl D, George J. Support vector machines combined with feature selection for prediction of maximal oxygen uptake. In: International Symposium on Engineering, Artificial Intelligence and Applications. Kyrenia, North Cyprus; Girne American University. 2014:3–4. | |
Silva G, Oliveira NL, Aires L, Mota J, Oliveira J, Ribeiro JC. Calculation and validation of models for estimating VO2max from the 20-m shuttle run test in children and adolescents. Arch Exerc Health Dis. 2012;3(1–2):145–152. | |
Daros LB, Osiecki R, Dourado AC, et al. Maximum aerobic power test for soccer players. J Exerc Physiol. 2012;15(2):80. | |
Veronese da Costa A, Manoel da Cunha C, Melo de Oliveira SF, Lima de Albuquerque F, José de Sá Pereira Guimarães F, Barbosa TM. Validation of an equation for estimating maximal oxygen consumption of nonexpert adult swimmers. Open Access J Sports Med. 2013;4:19–25. | |
Machado FA, Denadai BS. Predição da potência aeróbia (VO2max) de crianças e dolescents em teste incremental na esteira rolante. [Prediction of aerobic power (VO2max) of children and adolescents during an incremental treadmill test]. Motriz. 2013;19(1):126–132. Portuguese. | |
Aktürk E, Akay MF. Prediction of maximal oxygen uptake using multilayer perceptron combined with feature selection. In: 7th Engineering and Technology Symposium. Ankara, Turkey; Çankaya University. 2014:3–6. | |
Akay MF, Abut F, Daneshvar S, Heil D. Prediction of maximal oxygen uptake of cross-country skiers using different regression methods. In: International Symposium on Engineering, Artificial Intelligence and Applications. Kyrenia, North Cyprus; Girne American University. 2014:18–19. | |
Coquart JB, Eston RG, Grosbois JM, et al. Prediction of peak oxygen uptake from age and power output at RPE 15 in obese women. Eur J Appl Physiol. 2010;110(3):645–649. | |
Akay MF, Zayid EIM, Aktürk E, George JD. Artificial neural network-based model for predicting VO2max from a submaximal exercise test. Expert Syst Appl. 2011;38(3):2007–2010. | |
Acikkar M, Akay MF, George JD, Delil M, Aktürk E. Artificial neural network models for predicting maximum oxygen uptake from submaxiaml exercise involving walking, jogging or running. In: International Symposium on Electrical and Electronics Engineering and Computer Systems. Lefka, North Cyprus; European University of Lefke. 2012:17–21. | |
Akay MF, Özsert G, George J. Prediction of maximal oxygen uptake using support vector machines from submaximal data. DEÜ Eng Fac Eng Sci J. 2014;16(483):42–48. | |
Billinger SA, Swearingen E, McClain M, Lentz AA, Good MB. Recumbent stepper submaximal exercise test to predict peak oxygen uptake. Med Sci Sports Exerc. 2012;44(8):1539–1544. | |
Tönis TM, Gorter K, Vollenbroek-Hutten MMR, Hermens H. Comparing VO2max determined by using the relation between heart rate and accelerometry with submaximal estimated VO2max. J Sports Med Phys Fitness. 2012;52(4):337–343. | |
Cao Z-B, Miyatake N, Aoyama T, Higuchi M, Tabata I. Prediction of maximal oxygen uptake from a 3-minute walk based on gender, age, and body composition. J Phys Act Health. 2013;10(2):280–287. | |
Akay MF, Inan C, Bradshaw DI, George JD. Support vector regression and multilayer feed forward neural networks for non-exercise prediction of VO2max. Expert Syst Appl. 2009;36(6):10112–10119. | |
Cao Z-B, Miyatake N, Higuchi M, Miyachi M, Tabata I. Predicting VO2max with an objectively measured physical activity in Japanese men. Eur J Appl Physiol. 2010;109(3):465–472. | |
Schembre SM, Riebe DA. Non-exercise estimation of VO2max using the International Physical Activity Questionnaire. Meas Phys Educ Exerc Sci. 2011;15(3):168181. | |
Jang T-W, Park S-G, Kim H-R, Kim J-M, Hong Y-S, Kim B-G. Estimation of maximal oxygen uptake without exercise testing in Korean healthy adult workers. Tohoku J Exp Med. 2012;227(4):313–319. | |
Shenoy S, Tyagi B, Sandhu J, Sengupta D. Development of non-exercise based VO2max prediction equation in college-aged participants in India. J Sports Med Phys Fitness. 2012;52(5):465–473. | |
Akay MF, Özsert G, Genc E, George J. Development of new non-exercise maximal oxygen uptake models by using support vector machines. In: International Symposium on Engineering, Artificial Intelligence and Applications. Kyrenia, North Cyprus; Girne American University. 2014:11–12. | |
Nielson DE, George JD, Vehrs PR, Hager RL, Webb CV. Predicting VO2max in college-aged participants using cycle ergometry and perceived functional ability. Meas Phys Educ Exerc Sci. 2010;14(4):252–264. | |
Akay MF, Zayid EIM, Aktürk E, Kale G, George JD. Artificial neural network-based model for predicting VO2max from a hybrid exercise test. In: 6th International Symposium on Electrical and Computer Systems. Lefka, North Cyprus; European University of Lefke. 2010:16–20. | |
Akay MF, Shokrollahi N, Aktürk E, George JD. Development of new VO2max prediction models by using artificial neural networks. In: International Symposium on Computing in Science and Engineering. Aydin, Turkey; Gediz University. 2011:39–44. | |
Yücel E, Akay MF, Aktürk E. Investigating the effect of questionnaire variables on the prediction of maximal oxygen uptake using multilayer perceptron and multiple linear regression. In: International Symposium on Engineering, Artificial Intelligence and Applications. Kyrenia, North Cyprus; Girne American University. 2013:35. | |
Akay MF, Abut F, Georg J. Using support vector machines to predict maximal oxygen uptake with the help of questionnaire variables. In: International Symposium on Engineering, Artificial Intelligence and Applications. Kyrenia, North Cyprus; Girne American University. 2014:5–6. | |
Wang L. Support Vector Machines: Theory and Applications. Springer Science and Business Media; Berlin 2005. | |
Delashmit WH, Missiles LM. Recent developments in multilayer perceptron neural networks. In: Proceedings of the 7th Annual Memphis Area Engineering and Science Conference; Memphis, TN, USA. 2005. | |
Specht DF. A general regression neural network. IEEE Trans Neural Netw. 1991;2(6):568–576. | |
Evrendilek F, Karakaya N. Monitoring diel dissolved oxygen dynamics through integrating wavelet denoising and temporal neural networks. Environ Monit Assess. 2014;186(3):1583–1591. | |
Evrendilek F, Karakaya N. Regression model-based predictions of diel, diurnal and nocturnal dissolved oxygen dynamics after wavelet denoising of noisy time series. Physica A. 2014;404:8–15. | |
Peng H, Long F, Ding C. Feature selection based on mutual information: criteria of maxdependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell. 2005;27(8):1226–1238. | |
Hall M. Correlation-based feature selection for machine learning, Ph.D. Thesis, Department of Computer Science, University of Waikato, 1999. |
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.