Back to Journals » International Journal of Nanomedicine » Volume 10 » Issue 1
Interstitial diffuse radiance spectroscopy of gold nanocages and nanorods in bulk muscle tissues
Authors Grabtchak S, Montgomery L, Pang B, Wang Y, Zhang C, Li Z, Xia Y, Whelan W
Received 14 December 2014
Accepted for publication 10 January 2015
Published 13 February 2015 Volume 2015:10(1) Pages 1307—1320
DOI https://doi.org/10.2147/IJN.S79246
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Thomas Webster
Serge Grabtchak,1,2 Logan G Montgomery,1 Bo Pang,3,4 Yi Wang,4,5 Chao Zhang,6,7 Zhiyuan Li,6,7 Younan Xia,4,8 William M Whelan1,9
1Department of Physics, University of Prince Edward Island, Charlottetown, PEI, Canada; 2Departments of Electrical and Computer Engineering, and Physics, Dalhousie University, Halifax, Canada; 3Department of Biomedical Engineering, Peking University, Beijing, People’s Republic of China; 4The Wallace H Coulter Department of Biomedical Engineering, Georgia Institute of Technology and Emory University, Atlanta, GA, USA; 5Key Laboratory of Green Synthesis and Applications, College of Chemistry, Chongqing Normal University, Chongqing, People’s Republic of China; 6Laboratory of Optical Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, People’s Republic of China; 7College of Physics and Optoelectronics, South China University of Technology, Guangzhou, People’s Republic of China; 8School of Chemistry and Biochemistry, and School of Chemical and Biomolecular Engineering, Georgia Institute of Technology, Atlanta, GA, USA; 9Atlantic Veterinary College, Charlottetown, PEI, Canada
Abstract: Radiance spectroscopy was applied to the interstitial detection of localized inclusions containing Au nanocages or nanorods with various concentrations embedded in porcine muscle phantoms. The radiance was quantified using a perturbation approach, which enabled the separation of contributions from the porcine phantom and the localized inclusion, with the inclusion serving as a perturbation probe of photon distributions in the turbid medium. Positioning the inclusion at various places in the phantom allowed for tracking of photons that originated from a light source, passed through the inclusion’s location, and reached a detector. The inclusions with high extinction coefficients were able to absorb nearly all photons in the range of 650–900 nm, leading to a spectrally flat radiance signal. This signal could be converted to the relative density of photons incident on the inclusion. Finally, the experimentally measured quantities were expressed via the relative perturbation and arranged into the classical Beer–Lambert law that allowed one to extract the extinction coefficients of various types of Au nanoparticles in both the transmission and back reflection geometries. It was shown that the spatial variation of perturbation could be described as 1/r dependence, where r is the distance between the inclusion and the detector. Due to a larger absorption cross section, Au nanocages produced greater perturbations than Au nanorods of equal particle concentration, indicating a better suitability of Au nanocages as contrast agents for optical measurements in turbid media. Individual measurements from different inclusions were combined into detectability maps.
Keywords: gold nanocages, gold nanorods, turbid media, porcine muscles, diffuse radiance spectroscopy, Beer–Lambert law, perturbation
Introduction
The last decade has witnessed an unprecedented growth in the use of gold nanoparticles (Au NPs) in biomedical applications as therapeutic and optical contrast agents.1–3 In both cases, Au NPs have to be delivered to intended locations in a biological sample, their presence must be confirmed, and their concentrations must be quantified. While efficient in vivo delivery of Au NPs to the targeted areas in tissues is a separate and complex problem by itself,4 optical detection of Au NPs in bulk biological tissues remains to be a formidable task complicated by multiple scattering in turbid media. Detecting Au NPs in cell cultures or relatively thin layers of tissues can be achieved using various optical microscopy techniques5 or optical coherence tomography.6 For thicker layers or organs, diffuse reflectance spectroscopy,7 photoacoustics,8 or nonoptical methods, such as computed tomography (CT),9 can be employed. All methods have their own merits and limitations. While superficial illumination and detection can be applied only to easily accessible regions of the body as limited by light penetration depth, some organs are more suitable for intracavitory or intraluminal interrogation. In intracavitory (via rectum, pleural and bladder cavities) or intraluminal (within the gastrointestinal tract, transurethral) applications, the light is applied inside a cavity of a surrounding tissue boundary or within a vessel. When none of these is an option, an interstitial application can be the last resort, albeit with an increased degree of invasiveness.
Optical spectroscopy has become a valuable addition to biomedical diagnostics because it provides biochemical information (via spectral identification) about endogenous and exogenous chromophores, including Au NPs, present in tissues.10 Continuous wave broadband vis–NIR light is the simplest and least expensive source that is used both in a conventional cuvette-based spectroscopy and diffuse light measurements in turbid media. Under optimal and well-controlled illumination conditions of the conventional spectroscopy, signatures of the characteristic localized surface plasmon resonance (LSPR) peaks in the measured absorption (or extinction, in a more general case) can be reliably established and quantitative information about optical properties of Au NPs can be extracted using the Beer–Lambert law. An important aspect of such measurements is to record a reference signal (usually, water) under the same illumination conditions. This reference can be used to determine the power of incident light, eliminate the contribution from a solvent, as well as correct for a spectral response of the setup. Performing similar analysis of analogous measurements in turbid media is complicated by the necessity of accounting for both absorption and scattering events for diffused photons. Instead, more complex models are developed that consider photon migration and express, for example, the diffuse reflectance in the diffusion approximation.11 Then, optical properties of the turbid medium with Au NPs can be obtained by fitting experimental spectra to the model.7 A clear understanding of how the measured quantity is related to optical properties of Au NPs is of paramount importance in such studies.
In their seminal papers, Feng et al12 and Colak et al13 offered a way of treating localized inclusions of absorbers or scatterers in turbid media via the perturbation approach. In this approach, a signal in the presence of inclusion was expressed as a sum of two terms, a response from the medium without the inclusion and a response from the inclusion only. Both terms were presented via analytical forms using certain approximations to solve the diffusion equation and proper boundary conditions. Later, researchers have advanced the perturbation technique by developing more accurate and sophisticated algorithms.14–16 Still, extracting optical properties of localized absorbers from such models is not an easy task. Besides, treatment of spectrally resolved perturbation is not very common, and most models consider a perturbation at a fixed wavelength. While some Au NPs are more efficient absorbers than the others due to a larger absorption cross section, all NPs can be treated in the same way as long as they produce the same perturbation values.
Most perturbation approaches were developed for isotropic detectors that measure light in the entire 4π solid angle (ie, fluence). Since a single pair of fluence detector and light source cannot provide spatial information about inclusion’s location, a combination of multiple sources and/or detectors is required for this purpose (eg, arrays employed in diffuse optical tomography, [DOT]).17 On the other hand, radiance,18,19 which is an enabling technique in the current work, measures light power collected in the infinitesimal solid angle in turbid media. A special angular sensitive detector made from a side-firing fiber is usually required to measure the angular distribution of light in a selected location in turbid media. Hence, the technique provides some spatial information in addition to spectroscopic data, expanding the horizons of possible biomedical applications.
In this work, radiance spectroscopy is applied to the interstitial detection of localized inclusions made of aqueous suspensions of Au nanocages (NCs) and nanorods (NRs) embedded in porcine muscle phantoms. The principle of the measurements resembles conventional spectroscopy except that a light source, a capillary holding the sample with Au NPs, and a detector are surrounded by a turbid medium. Instead of a collimated light beam, the inclusion is illuminated by diffuse light from various directions. Similar to conventional spectroscopy, different samples are inserted sequentially into the muscle at the same location. We present both novel data and novel data analysis. With a proper reference sample, it is possible to apply the classical Beer–Lambert law for data analysis in the presence of turbid media. In particular, the goal of the work is to demonstrate 1) how the spectroscopic signatures of various types of Au NPs depend on particle concentrations and illumination conditions in bulk biological tissues; 2) how perturbation-based analysis can lead to extraction of optical properties of Au NPs and distance-related variations; and 3) how individual measurements can be assembled into Au NPs detectability maps. It is important to note that we did not restrict our analysis to any particular model for the propagation of light in turbid media.
Materials and methods
Radiance spectroscopy
The experimental setup used in the current work has been described in great detail in a number of publications.20,21 A schematic of the experimental setup is shown in Figure 1. Illumination was achieved with a 20 W tungsten halogen white light source (Ocean Optics, Dunedin, FL, USA) that was connected to a fiber with 2 mm spherical diffuser at the end. The detector was a 600 μm side-firing fiber (Pioneer Optics, Bloomfield, CT, USA) connected to a miniature spectrometer USB 4000 (Ocean Optics). The detecting fiber was held in a computer-controlled rotation stage that provided the full 360° rotation with 0° angle corresponding to detector facing the source. Illumination and detection were performed interstitially by inserting the fibers into the tissue at predetermined locations. Both illuminating and detecting fibers were threaded through 15-gauge needles for mechanical stability but only the protruding part of the detecting fiber was inserted into the phantom to reduce self-scattering effects. All interstitial measurements required puncturing the phantom with 15- and 17-gauge needles to produce holes that would accommodate the illuminating and detecting fibers, correspondingly. In all phantoms the illuminating fiber was always placed ~5 mm away from the edge of the phantom, and the detecting fiber was inserted 15 mm away from the illuminating fiber along 0°. The porcine phantom was held in a black plastic holder with an internal diameter of ~40 mm. The distances were measured with a ruler, with the uncertainty of ±0.5 mm. Radiance data were acquired by rotating the side-firing fiber over a 360° range with a 2° step and collecting spectra with an USB 4000 at every angular step.
Radiance measurement protocol
For every phantom, a reference data set of radiance I0 (R, λ, θ) was obtained prior to inserting the inclusion, where R is the source–detector distance, λ is the wavelength, and θ is the scattering angle relative to the direction of the source (0°). The phantom was punctured with a needle, producing two holes for the intended 15 mm source detector separation. Next, the detecting and illuminating fibers were inserted half-way through and aligned vertically by maximizing the signal. Spectra were recorded starting with the detector facing 0° with 2° increments (180 spectra in total). To accommodate the inclusion capillary tube, a hole was made in a desired location while keeping both illuminating and detecting fibers in the phantom, and the tube was carefully placed in it. This procedure was followed for all angles of the inclusion location except for 0°. For this angle, due to proximity effects, both detecting and illuminating fibers were taken out prior to inserting the inclusion. Measurements were repeated and the new data set I0+Au (R, λ, θ) was produced. Every data set was a matrix, with the first column containing wavelengths and the other columns corresponding to radiance measured from −180° to 180° angles. Radiance extinction ratio, RER (R, λ, θ) = I0 (R, λ, θ)/I0+Au (R, λ, θ), matrix was produced via element by element division of two matrices. Once the measurements were completed with a particular inclusion, it was withdrawn from the sample and the next one from Table 1 was placed in the same location until all 10 were measured. For every new location of the inclusion, the new fresh phantom was cut and the entire procedure described earlier was repeated. Then RER data were presented as contour plots called spectro-angular maps.
  | Table 1 Samples information |
Detectability maps assembly protocol
The inclusion was initially inserted at one of the selected angles and 3 mm away from the detector (the starting distance), followed by RER spectro-angular map measurements, as was described previously. Then, the inclusion was moved to a new position with 2 mm increments (ie, to 5, 7 mm, etc) in new phantoms every time with another spectro-angular measurement. Such translations were performed along angles of 0°, −45°, −90°, −135°, and −180° relative to the direction of the light source. Perturbation values were calculated from RER, and a single value corresponding to the angle–distance pair was carried to the new perturbation or detectability map. The obtained result was copied for the corresponding positive angle in the maps. It is understood that this procedure assumes mirror symmetry between left and right halves of the phantom, which may not hold true for heterogeneous samples. Otherwise, the complete mapping would require nearly 60 phantoms, which would be impractical. For every position of the inclusion, a new fresh porcine muscle phantom was used such that every map was a combined result from ~30 phantoms. This approach was followed to avoid effects from multiple holes or voids (produced after puncturing the phantom) on the light distribution (and hence, detectability) in subsequent measurements. The effects from voids were reported previously.22 Thus, every perturbation map reflects possible fluctuations in optical properties and morphology between multiple phantoms and should be treated as a synthetic data set of typical detectability rather than a map in the individual phantom. It was reported that that optical properties of multiple samples of analogous porcine muscle phantoms can fluctuate, with a standard deviation of ~30%.21
Muscle tissue samples
Porcine meat (pork loin center roast, boneless) was purchased at a local grocery store in ~0.8–1.0 kg packages on a day they were packaged. In total, six different packages were used in the experiments. The phantom was prepared by cutting a prostate-size piece (~4 cm diameter, ~3 cm thick) from a larger piece of meat. Every package produced 4–5 phantoms. Overall, measurements were performed on ~30 porcine phantoms that were combined into single synthetic maps for individual types of NPs. When not in use, the remaining porcine meat was stored in a fridge at +4°C. Each large package was consumed in ~2 days. According to porcine anatomy, the loin part corresponds to longissimus dorsi muscles. All individual phantoms were always cut perpendicular to muscle fibers. Optical properties of such porcine muscle phantoms were reported previously.21
Gold nanocages and nanorods
Gold NR (cethyltrimetylammonium bromide, CTAB capped) water solutions were obtained from Nanopartz Inc. (Loveland, CO, USA). Concentrated bare Au NR solution (6.2×1013 NPs/mL, 735 nm resonance, 10 nm diameter, ~33 nm length) was used as is (NR-100) and for volume dilution to prepare NR-10 (6.2×1012 NPs/mL) (Table 1). For the low-concentration NR sample (NR-1), a different solution was used (6.2×1011 NPs/mL, 805 nm resonance, 10 nm diameter, 41 nm length). While it was our intention to use Au NRs with 805 nm resonance for all measurements to facilitate a comparison with Au NCs having 805 nm resonance, highly concentrated Au NRs solutions with 805 nm resonance were not available at the time of experiments. On a single occasion (a manifestation of multiple Au NRs inclusions in the spectro-angular map), multiple inclusions were obtained from the Au NR solution with 6.2×1011 NPs/mL and ~690 nm resonance.
The Au NCs were fabricated by following the previously published protocol, using a galvanic replacement reaction between silver nanocubes and HAuCl4.23 The as-prepared Au NCs were washed twice with water and by centrifugation at 11,000 rpm for 10 minutes. The LSPR peak of the Au NCs was tuned to 805 nm, measured by Lambda 750 UV–Vis spectrometer (PerkinElmer, Waltham, MA, USA). The product was finally redispersed in water at a concentration of 8×1011 NPs/mL (stock solution), which was labeled as NC-100. All subsequent dilutions were obtained by following the “dilution by 2” protocol: equal volumes of the solution and water were mixed in a vial, with a small portion (~24 μL) taken to fill 1 mm capillary tube. Then, the newly obtained solution was diluted by a factor of 2 again. The geometry parameters of the Au NCs such as the edge length, wall thickness, and pore size were measured to be 54.6±3.0, 7.1±1.0, and 30.1±1.8 nm, respectively, with transmission electron microscopy (TEM, Hitachi 7700, Tokyo, Japan). The content of Au (44.5%) and Ag (55.5%) in the Au NCs was measured with inductively coupled plasma mass spectrometry (NexION 300Q, Perkin Elmer).
Modeling of optical properties of gold nanocages
In the numerical simulations we used the three-dimensional finite-difference time-domain (3D-FDTD) method to calculate the scattering and absorption spectra of the Au NC, where plane wave light is assumed to excite the single nanoparticle. From the spectra, the LSPR can be clearly identified. In the simulation, the edge length, wall thickness of the shell, and diameter of the pore are set to be 54.6, 7.0, and 30.1 nm, respectively, as were measured using TEM.
Results and discussion
Optical characterization of Au nanocages and Au nanorods
Table 1 summarizes data for various types of Au NCs and NRs that were used in the study. Vis–NIR spectroscopy was employed for measuring the absorbance in a 1 mm rectangular cuvette, which was converted to the extinction coefficient, μext, for the corresponding NPs using the Beer–Lambert law (Figure 2). Several solutions of high concentrations (NC-100, NC-50, and NR-100) were too opaque for the measurements and absorbed almost all incident light in the 600–950 nm range. Characteristic flattening of the spectra near a saturation limit can be seen for these samples in Figure 2. Such spectra are not of any practical use in conventional spectroscopy measurements. From a linear part of the absorbance vs concentration dependence (Figure S1), the extinction cross section was estimated to be Cext=3.1×10−14 m2 for Au NC. The results of FDTD calculations for the NC produced the following numbers for the absorption, scattering, and extinction cross sections: Cabs=3.89×10−14 m2, Csca=1.98×10−14 m2, Cext=5.87×10−14 m2, respectively. For Au NR, the calculated values for the longitudinal plasmon resonance were supplied by the manufacturer, Nanopartz Inc.: Cabs=3.5×10−15 m2, Csca=3.8×10−16 m2, Cext=3.8×10−15 m2. One can see that while both types of NPs can be considered as dominant absorbers (albeit with some contribution from scattering for NC), the absorption efficiency of a single NC is expected to be theoretically at least an order of magnitude (~11) higher than that of one of an NR and the extinction to be higher by a factor of ~15. Note that it assumes ideal illumination conditions for NRs; for example, all NRs should be oriented parallel to the polarization vector of the monochromatic light. However, spectroscopic measurements produced values of μext, 1.9 and 1.5 mm−1 from two solutions with N=6.2×1012 NRs/mL (NR-10) and N=5×1010 NCs/mL (NC-6.25), which corresponds to a factor of ~124 differences in concentrations. It indicates that an experimental value of Cext=μext/N of an individual NC is higher than that of one of an individual NR by a factor of ~98 (vs ~15 theoretically). In experiments with unpolarized light and unknown orientations of NRs, the strength of absorption will depend on a fraction of light that can couple to and excite longitudinal plasmon oscillations in the NR solution. Thus, lower values of the effective absorption cross section for NRs will be measured, indicating that theoretical values were overestimated. This can explain the discrepancy between the theoretical and experimental ratios of Cext for NRs.
Spectro-angular maps of Au NP inclusions in porcine muscle phantoms
Some representative spectro-angular maps of the inclusions in the muscle phantom are shown in Figure 3A and B. Assembling multiple spectra measured in −180° to 180° range and obtaining the radiance extinction ratio, RER=I0/I0+Au (I0 radiance for the sample without the inclusion, I0+Au radiance for the sample with the inclusion), resulted in a contour plot that delineated areas of highest extinction (shown in red) both in the angular and in the spectral domains, ie, the spectro-angular map. We obtained such maps for all ten inclusions (Table 1) sequentially positioned with 2 mm increments starting with 3 mm distance from the detector at 0°, −45°, −90°, −135° and −180° angles (as in the right panel in Figure 1). Figure 3A corresponds to the inclusion made from NC-12.5 and positioned at 0° angle and 5 mm away from the detector. One can see that highest RER values are found at ~0° and ~800 nm, thus allowing for localization of the inclusion in the angular domain and identification of the spectral signature (LSPR) of the inclusion. Figure 3B shows the map for the inclusion made from NC-100 with the intended position at −45° and 3 mm distance from the detector. (The angular offset of ~15° due to inaccuracy in the sample’s placement is seen.) A very distinct characteristic of this sample is spectrally featureless extinction that remains almost flat in the entire 650–900 nm range. Such a signature makes impossible the identification of the inclusion as it does not display any plasmon resonance features. Similar to conventional vis–NIR spectroscopy measurements, such featureless extinction is caused by an optically opaque inclusion containing a high concentration of NPs that absorb all incoming light.
Understanding such spectral changes during measurements in turbid media is of practical importance for detection and identification of localized chromophores in bulk biological tissues. For example, during optical detection of Au NPs accumulated in a malignant area via passive or active targeting, one typically has limited knowledge of the NP density or photon fluence, such that a flat, featureless spectral response could be a result of a deficit of photons.
Since the contour plots from Figure 3 are merely collections of individual RER spectra presented vertically against corresponding angles, a spectral response at a particular angle can be selected and plotted in a conventional X–Y format once the angular location of the inclusion has been determined. This is illustrated in Figure 4A, which shows ten RER spectra for all inclusions (Table 1) inserted and measured sequentially in the same location inside the phantom, 3 mm away from the detector and −45° angle. The observed behavior is qualitatively very similar to the one displayed in Figure 2: a flat spectral response for high concentrations (NC-100, NR-100, NC-50), with a gradual transformation (NC-25) to spectral responses displaying characteristic LSPR signatures (NC-12.5, NR-10, NC-6.25, NC-3.125, NC-1.5625, NR-1).
Analysis of data with perturbation approach
A starting point of the perturbation approach is to express the measured signal as a sum of contributions from the background medium and the inclusion. Radiance measured in the current study can be presented as I0+Au=I0+ΔI, where ΔI is the perturbation contribution from the inclusion containing Au NPs. In the context of the current work, it is essential to understand the role of the inclusion in probing photon distributions. Due to the diffuse nature of photon migration in turbid media, photons traverse various parts of the phantom before reaching the detector. In the absence of the inclusion, some photons pass through the area that will be later occupied by the inclusion. Thus, the absorptive inclusion removes from further transport only those photons whose pathways have been intercepted by the inclusion. Essentially, the inclusion tags certain photons, and the efficiency of photon removal determines the degree of perturbation.
Rearranging the expression for RER=I0/(I0+ΔI), one can express the perturbation term normalized by the unperturbed radiance (ie, the relative perturbation) as follows: ΔI/I0=1/RER-1. This quantity is presented for all inclusions in Figure 4B using RER values from Figure 4A. Note that it has a negative sign because adding the inclusion reduces original radiance values. It is clear from Figure 4B that the greatest perturbation is obtained for inclusions with highest values of μext.
Since nearly constant values of ΔI/I0 for NC-100 and NR-100 (Figure 4B) indicate that almost all photons incident on the sample have been absorbed, this perturbation term can be converted to the density of photons that originate from the source, pass through inclusion’s location, and reach the detector, normalized by the total density of photons that are collected by the detector in the absence of the inclusion (ie, the relative incident photon density or incident radiance). In order to present it as the incident radiance, one has to drop the negative sign. Next, in order to obtain a relative transmitted light intensity for each type of inclusion with this new value of incident radiance, one has to subtract the absorbed part from the incident one as follows: |ΔI100/I0|−|ΔIx/I0|, where ΔI100 corresponds to the inclusion extinguishing all local density of photons and ΔIx to inclusions that provide other lower levels of absorption. The results of such operation are shown in Figure 4C. Then, taking a natural logarithm of the ratio of incident to transmitted radiance eliminates I0 and produces the following expression: ln(|ΔI100|/(|ΔI100|−|ΔIx|)). Note that it corresponds to the left part of the classical Beer–Lambert expression (ie, the incident over transmitted optical power): ln(ΔI100/(ΔI100−ΔIx))= μext·L, where L is optical path equal to the length of the cuvette (note that we dropped the modulus signs in the expression, keeping it in line with the conventional form). In our experiments, L corresponds to a diameter of a capillary tube (1 mm) filled with solutions of Au NPs and embedded in the porcine phantom. Results of extracting μext from the radiance-based Beer–Lambert expression are presented in Figure 4D. One can see that inclusions based on NC-50 and NC-25 produced very strong absorption, leading to nearly saturated values in a wide spectral range. This is not surprising because the same light source was used both in conventional spectroscopy and diffuse light measurements. Thus, the optical power delivered to the inclusion in a 1 mm capillary tube in diffuse light measurements is expected to be much lower than the one incident on the 1 mm thick rectangular cuvette under the ideal and well-controlled illumination conditions such as with conventional spectroscopy measurements. As a result, the inclusions based on NC-50 and NC-25 were capable of absorbing nearly all photons under diffuse light illumination. Data from other inclusions appear to agree reasonably with those obtained from conventional spectroscopy measurements (Figure 2): 1.9 vs 2.4 mm−1 (NC-12.5), 1.5 vs 1.8 mm−1 (NR-10), 0.7 vs 1.5 mm−1 (NC-6.25), 0.4 vs 0.75 mm−1 (NC-3.125), 0.2 vs 0.4 mm−1 (NC-1.5625 and NR-1).
Following the same procedure, values of μext were obtained from measurements at other angles and distances. Some representative plots are shown in Figure 5A–C for 0° and 5 mm distance (5A), for −90° and 3 mm distance (5B), and for −135° and 3 mm distance (5C). With minor variations, the results are consistent with those presented in Figure 4D, with a tendency of displaying the highest error at lowest values of μext. (Note that the scan for NC-25 inclusion turned out to be unreadable and thus was absent for −90° and 3 mm combination.) Hence, all results conclusively demonstrate that the strength of the inclusion’s perturbation, ΔI, can be converted to μext in diffuse radiance measurements.
In an attempt to minimize measurement errors and uncertainties, both the detecting and illuminating fibers were kept inside the phantom during the insertion and withdrawal of Au NPs-filled capillary tubes (except measurements of the inclusion positioned at 0°). However, inserting a capillary tube even in the same location in the heterogeneous phantom was a delicate task. It caused inadvertent tissue movement that could change the tissue arrangement near the detector and the light source and, as such, trigger undesired changes in the density of photons reaching the detector. Hence, it would result in unavoidable fluctuations in the measured signal. We believe that this was the main source of error in our measurements. Other possible sources of error include 1) the presence of the thin-wall quartz capillary tube, which would scatter incident photons with certain trajectories and prevent them from interacting with Au NPs (this effect will be more pronounced for tubes filled with Au NP solutions having lower μext, as was seen in the current work); 2) the assumption that both weak and strong perturbations can be correctly accounted for by the same expression used in the work (ie, linearity); and 3) the assumption that photons follow the same pathways in the tissue and inserting inclusions only interrupts their transport in the existing trajectories but does not redistribute them to new areas of the sample. With all these factors, it is not surprising to see a difference between the values of μext obtained from conventional spectroscopy and diffuse radiance measurements (with the latter always underestimating μext).
It is remarkable to see that the described approach can be applied both in the transmission and in the reflection geometries while the Beer–Lambert law is defined for the transmission geometry. (It becomes obvious when analyzing source–inclusion–detector photon pathways for various measurement geometries presented in the right panel in Figure 1.)
It is widely accepted that for Beer–Lambert law to be applicable, the medium should be homogeneous, the incident light should be collimated, and the reflection or scattering should not contribute to the loss of transmitted light.24 This is clearly not the case for biological tissues. In applications to measurements in turbid media, the Beer–Lambert law transforms to the modified Beer–Lambert law by introducing a scattering dependent light intensity loss parameter and a differential path length factor.25–27 Typical applications of this modified formula are focused on extracting the total hemoglobin concentration and tissue oxygen saturation for chromophores distributed in the tissue.28 (See also this review for extensive references on detailed theoretical analysis of the modified Beer–Lambert law.)
Thus, it has been demonstrated in the current work that the original Beer–Lambert law can still be applied in turbid media to extract optical properties of the localized Au NP inclusion as long as the incident photon density can be correctly assigned to the detector. Hence, the ability of Au NPs to tag certain photons in experiments in turbid media is essential for this purpose. To the best of the authors’ knowledge, this is the first experimental demonstration of the direct application of the original Beer–Lambert law to a localized inclusion in turbid media. As opposed to conventional spectroscopy measurements, the proposed approach does not require the knowledge of all photons incident on the sample (from all possible directions) and collection of all photons that pass through the sample. Instead, only a fraction of photons is followed, and the effect of the inclusion on this fraction is recorded, a sort of spatial filtering that is provided by the angular-sensitive detector. Extending the analogy to conventional spectroscopic cuvette measurements, obtaining the proper reference signal is required in both approaches. The reference signal serves the same purpose of measuring the intensity of light incident on the sample, which is achieved by inserting a totally transparent (conventional spectroscopy) or totally absorbing sample (diffuse radiance spectroscopy) in the location of the sample of interest.
This result is important from both fundamental and applied points of view. Once photons interacting with the inclusion have been isolated, the applicability of the classical Beer–Lambert law for turbid media becomes straightforward and does not require any modifications or introducing any effective parameters. This has a fundamental significance. However, the accuracy of determining both incident and transmitted photon density is more demanding in the proposed approach and inevitably suffers because of the invasive nature of the experiment and other reasons discussed previously. Then, it is reflected in values of μext extracted from experiments. In spite of the principal applicability of Beer–Lambert law for extracting optical properties of a localized inclusion, we do not expect that the approach can be applied as is when detecting Au NPs delivered to targeted sites in biological tissues. Obtaining a proper reference signal may not be possible, and inserting a capillary tube with highly concentrated Au NPs is out of question. However, it leads to a better understanding of spectral signatures of Au NPs observed in bulk tissues, and being able to measure μext even in well-controlled turbid systems is the first step closer to the quantification of Au NPs in less-controlled ex vivo and in vivo tissue applications.
While we have constantly referred to the extracted quantity as μext, in fact, it should be μa. It was shown previously20 that for 250 nm Au NPs being dominant scatterers, radiance measurements in turbid media were sensitive only to the absorption contribution. For 250 nm Au NPs, absorption and scattering components in μext have very distinct spectral signatures due to high-order mode, quadrupole contributions to the μsca. Hence, detected signatures coincided with μa, indicating that resolving a contribution from μsca of Au NPs in highly scattering media with interstitial radiance technique can be difficult.
Analyzing the experimental dependence of ΔI/I0 on the distance between the inclusion and the detector (r) revealed that, within measurements accuracy, ΔI/I0·r= constant. Supporting data are demonstrated in Figure 6A and B, which plots −ΔI/I0 vs concentration of the NCs, N for inclusions positioned at various distances from the detector, r at −45° (6A) and −90° (6B) angles at the wavelength of the plasmon resonance (805 nm). Experimentally measured data points are presented, with different symbols corresponding to different values of r. The solid lines were obtained from the data set measured at r=3 mm and the use of ΔI/I0·r= constant to predict the perturbation produced at other distances (ie, 5, 7 mm, etc). The match between the symbols and the lines is reasonable, given the fact that every new distance was measured in a new muscle phantom that may have different optical properties and a different degree of heterogeneity. The data set measured at 9 mm at −90° (Figure 6B) is likely the result of the very strong tissue heterogeneity that pushed the perturbation values to be lower than those measured at 11 mm in a different muscle tissue. Thus, in the absence of a rigorous theoretical expression, the established empirical relation can serve as a guide for predicting the perturbation variation with distance in diffuse light measurements involving localized Au NC inclusions.
Detectability (or perturbation) mapping
Photon migration in heterogeneous turbid media often produces light distributions that can differ significantly from those in homogeneous turbid media. Mapping such distributions can be a sole focus of some studies. However, when such maps have been obtained with the help of Au NP inclusions as in the current work, they also carry information about detectability of the inclusions in corresponding turbid media. The current study focuses on the detectability aspect.
Some representative examples of detectability maps composed from multiple measurements with various inclusions (NC-100, NC-12.5, NR-10) are shown in Figure 7A–C. In these maps, variations in perturbation are presented with red color corresponding to high perturbation values, blue to lowest values, and black highlighting areas with no detectable signal from the inclusion. These maps combine measurements from multiple phantoms containing the inclusion in various locations.
There are common features and trends observed in all maps regardless of types of Au NPs. The highest perturbation values were detected in the vicinity of the detector for all angles. At the same time, measurements at 0° demonstrated the highest and at 180° the lowest perturbation values which is consistent with a preferential forward scattering of photons in biological tissues. As was indicated earlier, perturbation decayed with distance as 1/r for all angles except 0°. For 0°, perturbation values remained nearly constant after some initial decay (as in Figure 7A and B) or exhibited a slight increase toward the position of the light source (as in Figure 7C). Since it is known that the density of detected photons peaks near the detector and the light source (so-called banana plots),12 we believe that fluctuations in optical properties and heterogeneity of multiple phantoms interfered with observing the expected dependence and prevented us from uncovering it reliably (as opposed to analogous measurements in homogeneous turbid phantoms29). For the same reason, perturbation (measured at a fixed distance) decayed nonmonotonically with the angle changing from 0° to 180° and exhibited some spikes. In addition, a presence of 1/r dependence would make these measurements prone to demonstrating large variations at small r due to possible inaccuracies in the distance determination.
While the perturbation values go down with the μext as expected (Figure 7), the overall pattern in the maps appears to be preserved. It indicates that the distribution of photons remains nearly the same regardless of the properties of NPs that were used to probe it. The role of the NP inclusion is merely in detecting this distribution and providing a measurable response in a widest possible range of experimental conditions. Since the particle’s concentration is one of the important parameters, a higher-absorption cross section of an individual NC makes it a more efficient absorption-based contrast agent, compared with an NR, in optical measurements in turbid media. This is particularly important when considering cellular uptake of Au NPs by targeting specific surface receptors. While the process is very complex and depends on a number of factors (ie, the total number of receptors, the total number of Au NPs, the shape and size of NPs, targeting efficiency, nonspecific binding, etc), the efficient in vivo active delivery of Au NPs to targeted sites in biological tissues still has be demonstrated.4 In the meantime, it is highly desirable to detect the presence of Au NPs at lowest possible quantities per individual cell. A further optimization of Au NPs in terms of developing new types with even more increased absorption cross sections would be extremely beneficial for using Au NPs as cancer biomarkers in early cancer detection.
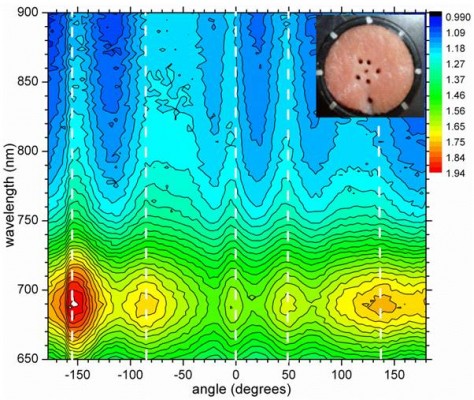
It should be noted that photon distributions and, as a result, detectability of inclusions can be manipulated or adjusted to some extent. An interesting effect was produced when several inclusions were placed simultaneously in a porcine muscle phantom. Five identical capillaries (2 mm diameter) containing the same amount of Au NRs (6.2×1012 NPs/mL, ~1 mL volume, plasmon resonance ~690 nm) were positioned at 5 mm distance from the detector (15 mm source–detector separation) at angles of 0°, 45°, −90°, 135°, and −160° (alternating angular positions in the left and right hemispheres of the phantom were chosen for practical reasons). A spectro-angular map demonstrating characteristic signatures of the inclusions is shown in Figure 8. When an individual inclusion is placed in the phantom, the highest RER values and, as a result, perturbation are produced for the inclusion positioned at 0°, decreasing to the lowest for 180°. This trend was completely reversed with five inclusions simultaneously present in the phantom. The highest values were observed for −160°, followed by 135°, −90°, 45°, and 0°, as seen in Figure 8.
  | Figure 8 Spectro-angular map of the phantom containing five inclusions of Au NRs (gold nanorods) positioned at 0°, 45°, −90°, 135°, and −160° (all 5 mm away from the detector as seen in the inset). |
Due to the diffuse nature of photon migration in turbid media, placing the inclusion at a certain distance at 0° removes photons that would visit a large part of the phantom in the forward scattering direction in the absence of the inclusion. In particular, a portion of photons would travel through a location of the inclusion at −160° before being backscattered and therefore registered by the detector. Thus, removal of photons increases because of a combined contribution from two (or more) inclusions. Similar qualitative arguments can be applied when explaining effects from inclusions (albeit with different contributions) at 45°, −90°, 135° on increased RER values at −160°. Because of the preferential forward scattering, highest effects will be observed for any inclusions located in a forward scattering cone, while an effect from the inclusion at −160° on RER values measured for 0° will be minimal. It is also important to stress that illumination conditions are most favorable for the inclusion located at 0° (because of the proximity to the light source), while the inclusions located at 135° and −160° receive the lowest number of photons. Overall, it emphasizes the fact that for detectability of the inclusion in turbid media, it is not enough to have the highest possible photon flux incident on the inclusion. It is mandatory to have sufficient density of photons that have right trajectories reaching the detector.
Thus, detectability of the inclusion depends on the perturbation produced by a particular type of NPs. Perturbation, on the other hand, is a combined effect from the absorption coefficient of Au NPs and the density of photons available for removal by the absorptive inclusion. The size of the inclusion determines the interaction volume from which photons will be removed. Therefore, with an increase in the inclusion’s size, the perturbation and, as a result, detectability at the corresponding distance will increase as well. Hence, inclusions of a larger size can be detected at larger distances from the detector. A choice of a 1 mm capillary for the current study was dictated mainly by practical reasons, ie, the smallest-diameter tube that could be filled with a long needle syringe.
Conclusion
In summary, we have quantified interstitial diffuse radiance measurements in porcine muscle phantoms containing localized inclusions of Au NCs and NRs using a perturbation approach. This approach enables separating contributions from the porcine phantom and localized inclusion, with the inclusion acting as a perturbation probe of photon distributions in the turbid medium. Positioning the inclusion at various spatial locations in the phantom allows for tracking of photons that originate from the light source, pass through the inclusion’s location, and reach the detector. The inclusions with high μext are capable of absorbing nearly all incident photons in 650–900 nm range, leading to a spectrally flat radiance signal. This signal can be converted to the relative density of photons incident on the inclusion. Then, experimentally measured quantities can be expressed via the relative perturbation and arranged into the classical Beer–Lambert law that permits extracting μext of various Au NP inclusions in the transmission and back reflection geometries. To the best of the authors’ knowledge, this is the first time the Beer–Lambert law has been applied experimentally without any modifications to determine optical properties of a localized inclusion in turbid media. It has also been shown that the spatial variation of the optical perturbation can be well described by 1/r dependence, where r is the distance between the inclusion and the detector. Due to a larger absorption cross section, Au NCs produce larger perturbations than do Au NRs of equal concentrations, indicating a better suitability of Au NCs as contrast agents for optical measurements in turbid media.
Acknowledgments
The authors acknowledge financial support from Natural Sciences and Engineering Research Council, the Canadian Institutes of Health Research, Atlantic Canada Opportunity Agency, and Undergraduate Student Research Award from Natural Sciences and Engineering Research Council (to Logan G Montgomery).
Disclosure
The authors report no conflicts of interest in this work.
References
Dykman L, Khlebtsov N. Gold nanoparticles in biomedical applications: recent advances and perspectives. Chem Soc Rev. 2012;41(6):2256–2282. | ||
Cai W, Gao T, Hong H, Sun J. Applications of gold nanoparticles in cancer nanotechnology. Nanotechnol Sci Appl. 2008;1(1):17–32. | ||
Huang X, El-Sayed IH, El-Sayed MA. Applications of gold nanorods for cancer imaging and photothermal therapy. Methods Mol Biol. 2010;624:343–357. | ||
Altinoglu EI, Adair JH. Near infrared imaging with nanoparticles. Wiley Interdiscip Rev Nanomed Nanobiotechnol. 2010;2(5):461–477. | ||
Sokolov K, Follen M, Aaron J, et al. Real-time vital optical imaging of precancer using anti-epidermal growth factor receptor antibodies conjugated to gold nanoparticles. Cancer Res. 2003;63(9):1999–2004. | ||
Boppart SA, Oldenburg AL, Xu CY, Marks DL. Optical probes and techniques for molecular contrast enhancement in coherence imaging. J Biomed Opt. 2005;10(4):041208. | ||
Zaman RT, Diagaradjane P, Wang JC, et al. In vivo detection of gold nanoshells in tumors using diffuse optical spectroscopy. IEEE J Select Topics Quantum Electron. 2007;13(6):1715–1720. | ||
Agarwal A, Huang SW, O’Donnell M, et al. Targeted gold nanorod contrast agent for prostate cancer detection by photoacoustic imaging. J Appl Phys. 2007;102(6):4. | ||
Popovtzer R, Agrawal A, Kotov NA, et al. Targeted gold nanoparticles enable molecular CT imaging of cancer. Nano Lett. 2008;8(12):4593–4596. | ||
Rolfe P. In vivo near-infrared spectroscopy. Annu Rev Biomed Eng. 2000;2:715–754. | ||
Farrell TJ, Patterson MS, Wilson B. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. Med Phys. 1992;19(4):879–888. | ||
Feng SC, Zeng FA, Chance B. Photon migration in the presence of a single defect – a perturbation analysis. Appl Opt. 1995;34(19):3826–3837. | ||
Colak SB, Papaioannou DG, ‘t Hooft GW, et al. Tomographic image reconstruction from optical projections in light-diffusing media. Appl Opt. 1997;36(1):180–213. | ||
Carraresi S, Tahani S, Martelli F, Zaccanti G. Accuracy of a perturbation model to predict the effect of scattering and absorbing inhomogeneities on photon migration. Appl Opt. 2001;40(25):4622–4632. | ||
Sassaroli A, Martelli F, Fantini S. Perturbation theory for the diffusion equation by use of the moments of the generalized temporal point-spread function. I. Theory. J Opt Soc Am A Opt Image Sci Vis. 2006;23(9):2105–2118. | ||
Martelli F, Pifferi A, Contini D, et al. Phantoms for diffuse optical imaging based on totally absorbing objects, part 1: basic concepts. J Biomed Opt. 2013;18(6):066014. | ||
Durduran T, Choe R, Baker WB, Yodh AG. Diffuse optics for tissue monitoring and tomography. Rep Prog Phys. 2010;73(7):07601. | ||
Barajas O, Ballangrud AM, Miller GG, Moore RB, Tulip J. Monte Carlo modelling of angular radiance in tissue phantoms and human prostate: PDT light dosimetry. Phys Med Biol. 1997;42(9):1675–1687. | ||
Dickey D, Barajas O, Brown K, Tulip J, Moore RB. Radiance modelling using the P3 approximation. Phys Med Biol. 1998;43(12):3559–3570. | ||
Grabtchak S, Palmer TJ, Whelan WM. Detection of localized inclusions of gold nanoparticles in Intralipid-1% by point-radiance spectroscopy. J Biomed Opt. 2011;16(7):077003. | ||
Grabtchak S, Montgomery LG, Whelan WM. Optical absorption and scattering properties of bulk porcine muscle phantoms from interstitial radiance measurements in 650–900 nm range. Phys Med Biol. 2014;59(10):2431–2444. | ||
Grabtchak S, Palmer TJ, Vitkin IA, Whelan WM. Radiance detection of non-scattering inclusions in turbid media. Biomed Opt Express. 2012;3(11):3001–3011. | ||
Skrabalak SE, Au L, Li X, Xia Y. Facile synthesis of Ag nanocubes and Au nanocages. Nat Protoc. 2007;2(9):2182–2190. | ||
Zourabian A, Siegel A, Chance B, Rode M, Boas DA. Trans-abdominal monitoring of fetal arterial blood oxygenation using pulse oximetry. J Biomed Opt. 2000;5(4):391–405. | ||
Delpy DT, Cope M, Vanderzee P, Arridge S, Wray S, Wyatt J. Estimation of optical pathlength through the tissue from direct time of flight measurement. Phys Med Biol. 1988;33(12):1433–1442. | ||
Sassaroli A, Fantini S. Comment on the modified Beer-Lambert law for scattering media. Phys Med Biol. 2004;49(14):N255–N257. | ||
Kocsis L, Herman P, Eke A. The modified Beer-Lambert law revisited. Phys Med Biol. 2006;51(5):N91–N98. | ||
Scholkmann F, Kleiser S, Metz AJ, et al. A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. Neuroimage. 2014;85:6–27. | ||
Grabtchak S, Callaghan K, Whelan WM. Tagging photons with gold nanoparticles as localized absorbers in optical measurements in turbid media. Biomed Opt Express. 2013;4(12):2989–3006. |
Supplementary material
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The
full terms of this license are available at https://www.dovepress.com/terms.php
and incorporate the Creative Commons Attribution
- Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted
without any further permission from Dove Medical Press Limited, provided the work is properly
attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.








