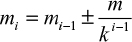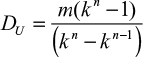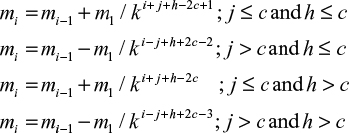Development of a randomized two-dimensional response surface pathway design with two interventional and one response variables

Background

Farming of Atlantic salmon has gradually become a large industry in Norway, accounting for a major part of the commercial industry along the coastline. A challenge with extensive farming is various diseases appearing in highly populated fish farms. One of the largest threats to the industry is the seasonal appearance of salmon lice (Lepeophtheirus salmonis). Salmon lice are a naturally occurring ectoparasite of salmon that attach themselves to the salmon skin. A few lice per salmon are not associated with health problems, but larger amounts are associated with ulceration of the skin, lower body weight, deteriorating fish health, and mortality. High degrees of lice infection in fish farms represent a serious epidemiological threat to the wild salmon and trout population. Control and treatment of salmon lice infections in fish farms is paramount to preservation of good fish health for both farmed and wild fish species.

Particulate CaO powder or burnt lime has been used in Japan, USA, and Norway to kill sea urchins. When CaO powder is distributed on test sites, it slowly sinks down to the sea floor and sticks to the surface of sea urchins, killing them after a few days. During work with spreading of CaO powder to facilitate revegetation of kelp forest¹ on test sites, it was observed that fish were swimming seemingly unaffected in and out of treatment clouds while becoming covered in the CaO powder. This indicated that sea urchins were more sensitive to the powder than the fish. If salmon lice were proven more sensitive to the particulate CaO powder than fish, the powder could constitute a new drug candidate for treatment against lice. In order to investigate this new treatment potential, a positive small-scale pilot test was conducted investigating dose range and administration time. In order to perform a dose–response study for use of CaO powder in full-scale industrial fish farms, the chosen study design needed to handle two interventional variables, dose and spreading duration, toward the optimal reduction in lice. Overriding clinical, ethical, and statistical goals for the controlled clinical trials was balancing the limited resources against compliance with 3Rs (reduction–refinement–replacement),² and an adaptive design approach was chosen.

The response surface pathway (RSP) design was published under this name for the first time in 2013.^3,4 However, the philosophy behind the model was launched back in 2001.⁵ In the medical and biological field, the lack of stochastic approach dominates study designs. In practical controlled clinical trials, all included procedures are standardized, and information generated during the study is as a rule ignored and completely lost. Included subjects in traditional clinical trials often generate important results during the study process. Information and results are not systematically captured or utilized for fine adjustment of direction choices between- or within-patient level. Systematic and in many cases potentially essential indicative information is therefore lost due to the lack of a stochastic study approach. The idea behind RSP is to capture and utilize the generated normative data during the study for faster and more accurately achieving valid and statistically powerful results. The latter includes important positive ethical implications within both human and veterinary research in addition to research and development cost savings.

The RSP method represents opportunities and interesting challenges especially when optimizing design for dose–response studies. The overriding idea behind the RSP method is systematic utilization of generated biological information between each design level in order to target the study goals faster, statistically stronger, and more accurately pinpointing interventional outcomes while reducing the number of included patients. Until now, the RSP method has only been documented with one interventional and one result variable while keeping the same number of patients in each design level and without use of randomization. Introducing new study dimensions, increasing the number of included patients with increasing design levels, and randomization between design levels could therefore add versatility and strengthen the RSP method.^3,6 Such a developed two-dimensional RSP design would be useful in determination of optimal efficacy dose and spreading duration of CaO powder in treatment against salmon lice. The aim of the present study is to describe an RSP design with two interventional and one result variables, combining between- and within-patient models and introducing a randomization procedure in a clinical situation.

Materials and methods

The material used in the development of this two-dimensional RSP design model consisted of 18 net pens with a daily mortality rate of <0.25%, no known concomitant disease, but infected by ≥5 salmon lice on average per fish. Each net pen was 160 m in circumference containing 100–200,000 salmon of ≥0.5 kg recruited from five Norwegian fish farms. One untreated control net pen was included at each location. The dose of particulate CaO powder and the spreading duration of CaO were the two interventional variables in the treatment of farmed Atlantic salmon against lice. The response variable was percentage reduction in lice with a starting dose of 6 g/kg biomass (bm) and 2 hours spreading duration. The study was approved by the Norwegian Animal Research Authority in accordance to the Norwegian Animal Welfare Act and the Norwegian Medicines Agency.

RSP design

The concept of RSP design has been previously presented both for within- and between patients³ with one interventional and one response variable. In the between-patient RSP design, dimension groups of three patients are allocated into sequences or the same number of patients as the number of levels in the design. In this between-patient dimension, the RSP design consists of n levels and r independent patient sequences. Each sequence contains the same number of patients as the number of levels in the design. One patient in the sequence receives the predefined starting dose.⁴ The response from this patient determines the dose for the second patient in the sequence. In general, the response from the patient at design level i (1≤i≤n) determines the dose for the patient at the next design level i+1. The sequences develop a random walk and describe a pathway with equal number of patients at each design level. In the within-patient RSP design, the patients are used as their own control and participate at all design levels. The RSP design previously presented in patient-related dose–response study uses equal number of patients at each design level. Development of the concept in laboratory animals and simulation demonstrated that this is not an optimal solution.⁶ By starting with a low number of patients at the first design level, and increasing this number with succeeding levels, the sample size reduces and accuracy of the estimates increases. In the within-patient situation, this procedure is impossible, but can be implemented in the between-patient RSP design by introducing a randomization.

Dose adjustment procedure in RSP design

The k adjustment factor was introduced to cover the upper and lower part of the dose window. Let D_u and D_l denote the upper and lower dose window, respectively. Let m denote the mid-dose in the dose window, m_i the dose at design level i, and k the dose adjustment factor. The dose at design level i is then given by the following equation:

(1)

The largest possible dose obtained at design level n will then be D_u = m_n−1 + m/kⁿ⁻¹. For i=1, m₁ ≡ m. With a known starting dose m and design level n, the k adjustment factor can be calculated using the formula for the sum of a geometric series^6,7 in the following equation:

(2)

Escalation and de-escalation procedure

The response variable is multinomial with equal number of categories denoted as 2c, resulting in 2c(n - 1) different pathways. Of these possible 2c response values, c gives escalation and the remaining c de-escalation of the interventional variable for the patients in the next design level.

The predefined window of the interventional variable is denoted as D_U = the upper and D_L = the lower limit. It may be convenient to use the mid value of the predefined dose window as the starting value. This will represent an assumed symmetrical distribution of the parameter in a Bayesian approach.⁸ A unimodal-skewed distribution would have given a starting value above or below the mid value and made it impossible to cover the dose window. In order to ensure coverage of the dose window the mid value is chosen and a dose adjustment procedure established.

Assume that the response variable has a sample space {1, 2,…,2c}. Let i represent the new design level, j the outcome from the previous dose level i-1, and h the outcome resulted in dose level i-1. For calculation of the second dose level h≡1 per definition, then for design level i≥2 the interventional value is given as:

(3)

Randomized between-patient RSP design

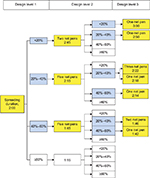
In order to optimize the RSP model, the number of patients is reduced to a minimum in the first design level and increases with increasing level. The recommended patient increase procedure is to start with three patients at level 1, increasing to 5, 7, 9, and so on at level 2 and upward (Figure 1). Assume that a₁ represents the number of patients calculated by the RSP procedure to receive the intervention A₁ in design level 2 based on the response obtained at first design level, a₂ the number of patients calculated to receive dose A₂, and a₃ those calculated for dose A₃ (Table 1). In general, a weighted randomization (a₁:a₂:a₃). If two interventions are equal (1=2) and one is different, the patients on the second level will be randomized (2:1). This means that the probability for a patient to be allocated to intervention A₁=A₂ is 2/3 and 1/3 for A₃.

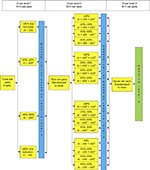Figure 1 Draft of the randomized between-patient response surface pathway design exemplified by the three level salmon lice study.

Table 1 Randomization of the interventional variable for the next design level in a 3-level between-patient RSP design Abbreviation: RSP, response surface pathway.

Based on responses obtained in the five patients in the second design level, theoretically five new interventional values (B₁, B₂, B₃, B₄, and B₅) allocate to the seven patients in the third design level. Assume that b₁ patients on the second design level are calculated by the RSP procedure to receive intervention B₁, b₂ to receive dose B₂, b₃ to receive dose B₃, b₄ to receive dose B₄, and b₅ to receive dose B₅. The interventional values used in the third design level for the seven new patients will allocate by weighted randomization (b₁:b₂:b₃:b₄:b₅) following the same procedure as explained for the second design level. In the case of design levels n>3, a similar procedure as described earlier will be used. By replacing the previously described sequence procedure for allocation of patients to design levels^3,4 with this randomization procedure, but keeping the other part of the RSP, a randomized between-patient one-dimensional RSP design is introduced. This randomization procedure assumes one response- and one interventional variable.

Two-dimensional RSP design combining randomized between- and nonrandomized within patient

In the randomized between-patient part, three net pens were treated with 6 g/kg bm CaO powder distributed to the net pen surface with a spreading duration of 2 hours. The percentage reduction in salmon lice corrected against the control net pen 7 days later was the recorded response variable. The classification of the response variable was chosen to be 1: <20% lice reduction; 2: 20%–40% lice reduction; 3: 40%–60% lice reduction; and 4: ≥60% lice reduction (Figure 1).

Depending on the obtained result in these three net pens the dose of CaO powder for the five next net pens in the second design level is determined by the previously described randomization procedure. The net pens allocated to the second level receive these determined doses distributed at the same 2 hours spreading duration (Table 2). The percentage reduction in lice 7 days later is recorded and used as a basis for the dose randomization of the seven net pens included in the third design level. As in the previous design levels, these net pens receive the determined doses of particulate CaO during the same 2-hour time interval.

Table 2 The particulate CaO dose based on percentage mean lice reduction at the prior design level in the between net pens situation

For the doses used in all the net pens at each design level in the between-patient part, the spreading duration was fixed to 2 hours. This spreading duration is the second interventional variable in the study and used in a nonrandomized within-patient RSP design.³ Depending on the lice reduction recorded 2 hours after finalizing the treatment, the spreading duration for the next CaO treatment of the same net pens was RSP calculated (Table 3). The duration between the three treatments of each net pen in the within-patient RSP part was 24 hours (Figure 2). This combination of randomized between-patient and nonrandomized within-patient RSP design results in a two-dimensional RSP design with two interventional variables and one common response variable.

Figure 2 The obtained pathways of CaO spreading duration (h: mm) in the within-patient study part. Note: The results based on percentage lice reduction after 24 hours uncorrected for the control net pens.

Table 3 Durations (h:mm) of administrations within each net pen based on percentage mean lice reduction at the prior design level

Statistical analysis

The sample space of the particulate dose and spreading duration of CaO may be expressed as Ω_D = {D_L≤….≤D_U} and Ω_A = {A_L≤….≤A_U}, respectively. Let µ_od and µ_a represent the optimal dose and spreading duration of particulate CaO and assume that µ_od and µ_a are contained in Ω_D and Ω_A, respectively. Minimum efficacy dose (MED) defines as the lowest dose µ_md resulting in at least 40% lice reduction. Assume µ_md ∈ Ω_D.

Maximal percentage lice reduction was estimated using polynomial regression with dose and CaO spreading duration as dependent variables.^8,9 The percentage reduction in lice assumed ordinal in both the interventional variables and the probability increases monotonically over the interventional levels. Isotonic regression was used for the estimation of minimum efficacy- and optimal efficacy dose and spreading duration.^10–12

Results

Two of the three net pens treated with 6.0 g/kg bm with 2 hours spreading duration on the first design level predicted an increase and one a decrease in the CaO dose (Table 4). Based on the obtained percentage reduction in salmon lice corrected for the untreated control net pens, the doses used for randomization of the five next included net pens in the second design level were 5.2 g/kg bm, 6.8 g/kg bm, and 8.2 g/kg bm. The randomization procedure resulted in one net pen receiving 6.8 and four receiving 8.2 g/kg bm with the same spreading duration of 2 hours. The obtained percentage reduction in lice after correction for the control net pens pointed to a dose decrease by all the five net pens in the second design level. One of the four net pens receiving 8.2 g/kg predicted a dose reduction to 7.9 g/kg bm and the three remaining predicted a reduction to 7.4 g/kg bm and was used for randomization to the third design level. The remaining net pen on the second level treated with 6.8 g/kg bm was predicted to be 6.5 g/kg bm (Table 4). The randomization to the third design level resulted in two net pens of 7.9 g/kg bm, four of 7.4 g/kg bm, and one of 6.5 g/kg bm with the fixed spreading duration of 2 hours. By mistake, three of the seven planned net pens allocated to 7.4 g/kg bm received 8.5 g/kg and due to weather conditions three other net pens became untreated. The pathway obtained by the RSP design resulted in an MED of 6.1 g/kg bm with an accuracy of ±0.3 g/kg bm (Table 5). The optimal efficacy dose was estimated to be 8.5 g/kg bm with an accuracy of ±0.5 g/kg bm. Despite the reduced sample size and the errors in the randomization, the accuracy of the estimates classifies as sufficient (Table 5).

Table 4 The obtained pathways of CaO dose in the randomized between-patient RSP part. The results expressed in percentage reduction in salmon lice after 7 days of treatment corrected for the control net pens Notes: aNet pen not treated. bErroneously used dose was 8.5 g/kg bm instead of 7.4 g/kg bm.cReduction ≥100% after correction in accordance with the control groups. Abbreviations: bm, biomass; RSP, response surface pathway.

Table 5 Estimated Minimum and Optimal Efficacy dose and spreading duration of particulate CaO Notes: The results expressed as predicted values with 95% CIs. aOnly uncorrected net pens included. Abbreviation: CI, confidence interval.

All the twelve included net pens in the within-patient RSP design receiving the CaO treatment administered in 2 hours in the first design level. The change in spreading duration was performed using uncorrected lice reduction in seven net pens, but by corrected results in the remaining five. The obtained uncorrected lice reduction after 24 hours resulted in a duration increase for all the seven net pens at the second within-patient design level (Figure 2). The recommended increase was 2 hours and 15 minutes for five net pens and 2 hours and 45 minutes for two net pens. The results obtained at the second design level recommended a further duration increase in six net pens and a reduction in one. In the statistical analysis, the obtained lice reduction was corrected using the control net pens recorded 7 days after initiation of treatment.

For the remaining five net pens, salmon lice were counted in the control net pens after each treatment and the change in spreading duration based on the corrected results. Two of these five net pens lack information on lice reduction in the second and third design level. A reduction to 1 hour and 45 minutes in spreading duration was recommended for the remaining three net pens. Based upon the results obtained in the second within-patient RSP design level, the spreading duration was increased for two net pens and reduced for one in the third level (Figure 2). Due to the difference in use of changing procedure after 24 hours two different clusters of net pens, regarding the within-patient RSP part, occurred. For those with corrections in percentage lice reduction the RSP design predicted the spreading duration to 1 hour and 46 minutes. In the uncorrected cluster of seven net pens, the minimum spreading duration was predicted to be around the starting value of 2 hours and increasing to 3 hours in order to obtain optimal efficacy (Table 5). The accuracy of the estimated minimum spreading duration was slightly better, but sufficient for both predictions.

The analysis detected an interaction between dose and spreading duration of CaO powder. Using a dose of 6 g/kg bm, the predicted spreading duration was 2 hours, increasing to 2 hours and 35 minutes for a CaO dose of 8.2 g/kg bm. The minimum efficacy combination was estimated to be 6.1 g/kg bm distributed during 2 hours. The optimal combination of dose and spreading duration of CaO was predicted to be 8.5 g/kg bm administered in 3 hours.

Discussion

Despite missing three of the planned 15 net pens and erroneous dose allocation of three net pens in the third design level the randomized between-patient RSP design was able to predict the minimum- and optimal CaO powder dose with sufficient accuracies. To perform such large-scale field trials is demanding. The net pens are 160 m in circumference and often located in harsh climatic conditions at sea. The obtained results are strongly influenced by weather conditions and administration method of CaO powder. These two factors give rise to significant variations in results and reduce the accuracy of the estimates.

The results obtained from the three first net pens recommended a dose increase for the second design level. Based on the obtained results from these five nets in the second design level the RSP model recommended dose reductions in the third design level to doses between 7.4 g/kg bm and 7.9 g/kg bm. The RSP procedure performed as planned up to the second design level and already pointed out the area of interest, underlining the assumed power of the design.^3,5 Only four of the allocated seven net pens were able to perform the treatment and three of these again received a substantially larger dose than recommended. These errors strengthen the estimation of the optimal efficacy dose but reduce the accuracy of minimum efficacy dose. In spite of these errors and missing data, the dose range given after the second design level covers the estimated optimal CaO dose. The accuracy of the predicted optimal efficacy dose characterizes as sufficient and, especially taking into account weather conditions and CaO administration method, it is very good. By random, the starting dose chosen to be 6.0 g/kg was close to MED and positively influenced the accuracy of the prediction. The randomization error in the second design level together with the missing data influenced the accuracy in the opposite direction. Despite this, the accuracy of the predicted MED was sufficient and underlines the strength of the RSP procedure. The present results indicate that the percentage reduction in salmon lice increases rapidly with increasing dose until reaching 7.8 g/kg bm, but continued with slight increase to the upper limit of the predefined dose window. The assumption in the statistical analysis model that the outcome variable increases monotonically over the interventional levels seems to be fulfilled and the suggested isotonic regression model is appropriate.¹⁰

The second interventional variable in this study was spreading duration of CaO powder onto the net pen surface performed as a three-level RSP within each net pen. For seven net pens, the decision of increasing or decreasing the spreading duration from one design level to the next was based on percentage reduction in lice without correction of the results from the control net pens for seven net pens. However, the control net pen correction was performed for three net pens, and information from the remaining two net pens regarding the spreading duration on second and third level was lacking. This difference in lice correction between the three design levels results in two clusters and obviously reduces the power of the analysis. As a rule, no corrections performed during the treatment within net pens and the uncorrected observations seem to be the correct procedure in such studies. The lice infection levels differ substantially between the participating fish farms during the study. The three fish farms with the highest infection levels participated with seven net pens while the other two farms participated with five. In the most infected net pens, the RSP procedure recommended increasing the spreading duration ending in a range from 2 hours and 14 minutes to 3 hours. For the five moderately infected net pens, the RSP procedure recommended reduction in the spreading duration. For two of these moderately attacked net pens only the lice reduction from the first design level and 7 days later was recorded. This clustering detected by the RSP design gave some additional information, but reduces the power related to the study aim. The spreading duration based on the corrected percentage lice reduction was substantially shorter than the one based on the uncorrected. Both with regard to the large deviation in lice attack between fish farms and the commonly used investigation procedure during treatment, the uncorrected spreading duration seemingly was pointing to the most accurate picture. The sample size of seven net pens used in the analysis is limited but is in accordance with a previous published study using within-patient RSP.^3,13 The accuracy of both the predicted minimum and optimal spreading duration classifies as sufficient. Taking into account the difficulties in performing such dose–response field study, the accuracy was far beyond expected.

It is likely to assume that the present reduction in lice increases with increasing spreading duration at least within a window and the obtained results verified this assumption. The reduction in lice increased to a certain level, kept constant, and then decreased. The demand to the statistical model was partly fulfilled, but this minor deviation will probably not influence the predicted value.

Factorial design is the most common and recommended design when estimating interactions between interventional variables. Replacing the present RSP design and predefining three values for each of the two interventional variables give a 3² factorial design. With the required number of observations in each cell, 54 net pens would have to be included. In addition to increasing the sample size by nearly four times, the use of such a model is lacking several options and combinations of both dose and spreading duration covered in the stochastic RSP procedure. The present study detected a positive interaction between dose and spreading duration of CaO. The optimal duration with a CaO dose of 6.0 g/kg for percentage lice reduction was ~2 hours and increased monotonically with increasing dose. The combined between- and within-patient RSP design into a two-dimensional model with two interventional and one response variables worked very well and made it possible to predict both the minimum and optimal efficacy CaO dose combined with spreading duration.^3,13 Previously performed simulation shows that 3+5+7=15 cases give sufficient statistical power.⁶ Due to the lack of three net pens, this study ended with 3+5+4=12 cases. The accuracy of the estimated minimum and optimal efficacy dose was reduced, but still sufficient for all practical uses. The sample size used in the within-patient part was in accordance with previous simulations and gave as well the possibility of subgroup analyses of the material. The error obtained by increasing or decreasing the spreading duration partly based on corrected and uncorrected percent lice reduction to a certain extent limited the value of the combined analysis. Despite this, the two-dimensional RSP model predicted both the minimum and optimal efficacy CaO dose and spreading duration with sufficient accuracy.

This two-dimensional RSP design has two interventional and one response variables, but may be as easily performed well with one interventional and two response variables. This may be achieved by combining between- and within-patient models. Questions to be answered are how to combine a between- and within-patient model into a two-dimensional RSP design and how to include two interventional and two response variables into the model?

Conclusion

Despite the lack of three included cases, erroneously allocated doses in three net pens at the third design level and use of corrected lice reduction during treatment, the two-dimensional RSP design detected its power and predicted the two interventional parameters in order to obtain minimum and optimal efficacy with sufficient accuracy.

Disclosure

The authors report no conflicts of interest in this work.

References

1.		Bernstein BB, Welsford RW. An assessment of feasibility of fusing high-calcium quicklime as an experimental tool for research into kelp bed/sea urchin ecosystems in Nova Scotia. Can Tech Rep Fish Aquat Sci. 1982;968:1–51.
2.		Russell WMS, Burch RL. The Principles of Humane Experimental Technique. London: Methuen; 1959.
3.		Dewi S, Kristiansen VM, Lindkær-Jensen S, Larsen S. Between- and within-patient, n-level Response Surface Pathway Design in dose-finding studies. Open Access J Clin Trials. 2014;6:63–74.
4.		Dewi S, Larsen S, Srimuninnimit V, Lu Y, Manuaba T, Lindkær-Jensen S. Benzene-poly-carboxylic acids complex with cis-diamminepolatinum (II) dichloride in the treatment of stage IV breast cancer patients. Open Breast Cancer J. 2013;5:7–15.
5.		Ryeng KA, Arnemo JM, Larsen S. Determination of optimal immobilizing doses of medetomidine-ketamine in captive reindeer (Rangifer tarandus tarandus). An iteration-designed controlled clinical study in wildlife medicine. Am J Vet Res. 2001;62:119–126.
6.		Dewi S, Aune T, Buanæs JAA, Smith AJ, Larsen S. The development of Response Surface Pathway Design to reduce animal numbers in toxicity studies. BMC Pharmacol Toxicol. 2014;15:18.
7.		Fisher G. Series and Sequences. Putney: Phoenix Education; 1996.
8.		Aster R, Borchers B, Thurber C. Parameter Estimation and Inverse Problems. 2nd ed. Oxford: Academic Press: Elsevier; 2012.
9.		Kleinbaum DG, Kupper LL, Muller KE. Applied Regression Analysis and Other Multivariable Methods. 2nd ed. Boston: PWS-Kent Publishing Company; 1988.
10.		Paul RK, Rosenberger WF, Flournoy N. Quantile estimation following non-parametric phase I clinical trials with ordinal response. Stat Med. 2004;23(16):2483–2495.
11.		Stylianou M. Advanced in and limitations of up-and-down methodology: a precis of clinical use, study design and dose estimation in anesthesia research. Anesthesiology. 2007;107(1):144–152.
12.		Stylianou M, Flournoy N. Dose finding using the biased coin up-and-down design and isotonic regression. Biometrics. 2002;58(1):171–177.
13.		Kristiansen V, Dewi S, Horsberg TE, et al. Tolerability and pharmacokinetic profile of a novel benzene-poly-carboxylic acids complex with cis-diammineplatinum (II) dichloride in dogs with malignant mammary tumours. Vet Comp Oncol. Epub 2015 Mar 12.