Back to Journals » ClinicoEconomics and Outcomes Research » Volume 9
Current recommendations on the estimation of transition probabilities in Markov cohort models for use in health care decision-making: a targeted literature review
Authors Olariu E, Cadwell KK, Hancock E, Trueman D, Chevrou-Severac H
Received 23 February 2017
Accepted for publication 22 June 2017
Published 1 September 2017 Volume 2017:9 Pages 537—546
DOI https://doi.org/10.2147/CEOR.S135445
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Prof. Dr. Dean Smith
Elena Olariu,1 Kevin K Cadwell,1 Elizabeth Hancock,1 David Trueman,1 Helene Chevrou-Severac2
1PHMR Ltd, London, UK; 2Takeda Pharmaceuticals International AG, Zurich, Switzerland
Objective: Although Markov cohort models represent one of the most common forms of decision-analytic models used in health care decision-making, correct implementation of such models requires reliable estimation of transition probabilities. This study sought to identify consensus statements or guidelines that detail how such transition probability matrices should be estimated.
Methods: A literature review was performed to identify relevant publications in the following databases: Medline, Embase, the Cochrane Library, and PubMed. Electronic searches were supplemented by manual-searches of health technology assessment (HTA) websites in Australia, Belgium, Canada, France, Germany, Ireland, Norway, Portugal, Sweden, and the UK. One reviewer assessed studies for eligibility.
Results: Of the 1,931 citations identified in the electronic searches, no studies met the inclusion criteria for full-text review, and no guidelines on transition probabilities in Markov models were identified. Manual-searching of the websites of HTA agencies identified ten guidelines on economic evaluations (Australia, Belgium, Canada, France, Germany, Ireland, Norway, Portugal, Sweden, and UK). All identified guidelines provided general guidance on how to develop economic models, but none provided guidance on the calculation of transition probabilities. One relevant publication was identified following review of the reference lists of HTA agency guidelines: the International Society for Pharmacoeconomics and Outcomes Research taskforce guidance. This provided limited guidance on the use of rates and probabilities.
Conclusions: There is limited formal guidance available on the estimation of transition probabilities for use in decision-analytic models. Given the increasing importance of cost-effectiveness analysis in the decision-making processes of HTA bodies and other medical decision-makers, there is a need for additional guidance to inform a more consistent approach to decision-analytic modeling. Further research should be done to develop more detailed guidelines on the estimation of transition probabilities.
Keywords: cost-effectiveness, decision models, probability, transitions
Introduction
Health technology assessment (HTA) and medical decision-making, more generally, rely on the use of decision-analytic models. Such models synthesize clinical, epidemiological, quality of life, resource use, and cost data in order to generate estimates of health effects and associated costs. Markov models are a popular form of decision-analytic models which characterize patient cohorts based on a finite number of mutually exclusive and exhaustive “health states”. Under the Markov property, membership of future health states depends only on the current health state, and not on the events that occurred before.1 Movement between health states is defined by “transition probabilities”, which determine the likelihood of a patient moving from one health state to another over a discrete period of time (the “cycle length”).1
An illustrative example of a three-state Markov model with health states 1, 2, and 3 is presented in Figure 1; an example of health states for a model of a general condition may be asymptomatic disease, symptomatic disease, and death. Movements between health states are governed by a matrix P of transition probabilities prs, which describes the risk of moving from state r to state s ≠ r at time r over a model cycle of length u, and prr, which describes the probability of remaining in state r at time r over a model cycle of length u. One health state (in this case health state 3, and usually the health state corresponding to death) will act as the “absorbing state”, for which the probability of moving to any other state is 0 and the probability of remaining in the state is 1.
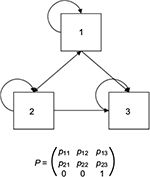  | Figure 1 Illustrative example of a three-state Markov model. |
Measures for cost and outcome can be associated with states and transitions to account for resource use during different stages of disease and the associated changes in health outcomes. These estimates of costs and outcomes may be accumulated over the course of the model and the cost-effectiveness of health technologies estimated.
The correct implementation of Markov models requires reliable and robust estimation of transition probability matrices (TPMs). In the simplest case, transition probabilities can be estimated in a straightforward manner using nonparametric methods based on observed counts for movements between health states in a data source. Briggs et al2 describe the methods for calculating probabilities in this scenario.
However, calculating TPMs is challenging when the inputs to the economic evaluation cannot be derived directly and completely from a single dataset; for example:
- How should TPMs be constructed when not all transitions are observed within a dataset?
Briggs et al2 note that feasible transitions might not always be observed in all datasets, implying 0% probability of these transitions occurring. The authors advise not to exclude potential transitions because they were not observed in the data. Alternatively, a prior distribution may be specified; commonly, 1 is added to each cell count.
- How should subgroup analyses be performed in Markov cohort models?
Subgroup analysis in Markov cohort models for economic evaluation is usually performed based on stratification of data, and estimation of transition probabilities at different values of t typically requires multiple partitions of the available data. This is often not an efficient use of data, and introduces many model parameters. An alternative approach is to allow covariate adjustment of the TPM. A growing body of literature has described these multi-state parametric models, which can be implemented in standard statistical software such as R, but have not yet been applied widely within economic evaluations for HTA submissions.3–5
- How should treatment effects from clinical studies and meta-analyses be applied?
It is common to apply relative effects to TPMs to estimate the probability of events for an intervention. Such treatment effects may be drawn from clinical trials directly or from formal evidence synthesis. Relative risks and odds ratios (unlike hazard ratios) are specific to the time period for which the event probabilities are defined. If the length of the trial or study reporting the relative risk (or odds ratio) is not the same as cycle length u, then applying this relative risk (or odds ratio) directly will be incorrect.6 Price et al6 present an adjustment to account for differences between the measured time point and the relative risk.
- How can we convert between alternative cycle lengths?
It is well known that in order to convert a probability from one cycle length to another (e.g., from annual to 6-months), it must be done by first converting to a rate.7,8 This is commonly achieved using the standard actuarial formula.9 However, conversion of a TPM from one cycle length to another is nontrivial; applying the actuarial formula to convert TPMs in models with more than two states introduces bias, because this ignores competing risk among states.10 More appropriate conversion requires taking the root of the matrix,10 or alternatively, choosing a short cycle length such that the probability of multiple clinical events occurring during a cycle is very small, thereby minimizing the bias.11
- How should model calibration be performed if direct estimation of inputs is not possible?
The objective of calibration is to “reverse engineer” the model of interest; essentially, to find input parameters so that the model predicts a known outcome (or outcomes). The analyst must make several decisions: there are multiple ways to define the objective function for the calibrated model, including approaches based on acceptable windows, minimizing deviation (absolute or in percentage terms), or the specification of likelihood functions. The selection of input parameters may also be performed using a number of methods. If multiple outcomes are to be calibrated against, and their input parameters are not independent, this can then become a complex optimization problem.12 Welton and Ades13 provide an illustrated example of how to calibrate transition probabilities to be consistent with information from a particular study.
- How should missing data be handled?
A commonly recommended strategy for addressing missing data within economic evaluations is multiple imputation.14 Under multiple imputation, each missing value is replaced with multiple predicted values; a vector of M≥2 possible values is created.15 M complete datasets are created, each with different imputations for the missing data. The datasets can then be analyzed together using standard statistical methods and uncertainty appropriately characterized using Rubin’s rules.15 In order to estimate transition probabilities nonparametrically following imputation, the analyst may, for example, assume that the observed value is represented by the mean of the values across the M datasets. However, this approach fails to recognize the uncertainty associated with the imputation process itself and as a consequence will underestimate uncertainty in the analysis. An obvious approach may be to estimate separate TPMs for each of the M datasets, and then sample between these alternative datasets in probabilistic sensitivity analysis. However, we are not aware of any studies assessing this.
Transparent and consistent decision-making relies on the availability of an accepted methodological approach to the calculation of TPMs; while individual researchers have contributed substantially to the discussion on these topics, the authors of the present study are not aware of any formal consensus statements or guidelines addressing questions such as those mentioned earlier. This targeted literature review therefore, sought to identify consensus statements or guidelines detailing how TPMs should be estimated for use in Markov models in the context of the economic evaluation of medical interventions.
Methods
A targeted literature review was performed to answer the following research question:
- What consensus statements or guidelines are available to inform the calculation of transition probabilities for use in Markov models for the economic evaluation of medical interventions?
Consensus statements were defined as “documents containing suggestions or recommendations based on the collective opinion of an expert panel” and guidelines as “systematically developed statements to assist researchers, HTA bodies, and other professionals in decisions about appropriate methodological approaches”.
Search methods
A base strategy was developed and refined to specifically target publications relevant to the research question.
Electronic database search
Search strategies specific to each database were designed to focus on retrieval of the published articles most likely to be relevant to the research question. The search strategies were designed and run by an experienced medical librarian.
The following electronic databases were searched:
- Medline (OvidSP)
- Medline In-Process Citations & Daily Update (OvidSP)
- Embase (OvidSP)
- PubMed
- The Cochrane Library, which includes six databases (Cochrane Database of Systematic Reviews, Cochrane Central Register of Controlled Trials, Cochrane Methodology Register, Database of Abstracts of Reviews of Effects, Health Technology Assessment Database, NHS Economic Evaluation Database)
Electronic searches were limited to English language publications. No country or time limits were applied. Details on the search strategy can be found in Figure S1.
HTA website search
The electronic search was supplemented by a literature search for relevant guidelines on HTA agency websites. The HTA agencies whose websites were searched are listed in Table 1. Reference lists of identified HTA guidelines were screened to identify additional relevant publications. No language limit was applied to searches of HTA websites.
  | Table 1 HTA agency websites considered Note: *Including NICE Decision Support Unit reports. Abbreviation: HTA, health technology assessment. |
Study selection
Identified publications were screened by one reviewer, with any publication considered to be informative to the research question being included. Study selection occurred in three phases:
- Potentially relevant publications were identified based on their title; any title clearly irrelevant was discarded at this stage.
- Abstracts or keywords were used to screen the remaining articles in order to identify relevant publications for full-text review.
- The full text of each potentially relevant publication was reviewed.
Studies were included if they were guidelines or consensus statements on the calculation of transition probabilities from either clinical endpoints of clinical trials or from clinical parameters of indirect/multiple treatment comparisons in Markov models. Publications that were not produced on behalf of professional organizations, expert panels, or HTA bodies were excluded.
Results
Electronic database search
The electronic database search identified 3,636 publications; 1,931 unique publications were identified following deduplication (Table 2).
  | Table 2 Results of the electronic database search |
Of the 1,931 unique publications identified, 1,788 publications were excluded on the basis of title review and 143 publications were excluded on the basis of abstract review. No guidelines on the estimation of transition probabilities for use in Markov models were identified via the electronic database search (Figure 2). However, 56 studies were considered to be of broad relevance, typically reflecting the viewpoints of individual authors or independent research groups as opposed to formal guidelines or recommendations. A list of the 56 publications considered to be of broad relevance can be found in Table S1.
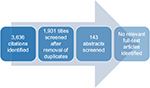  | Figure 2 Flow diagram of the screening process for the electronic database search. |
HTA website search
The HTA website search identified 10 guidelines on economic evaluation. However, no identified guidelines included guidance or recommendations on the calculation of TPMs. One relevant publication was identified following review of the reference lists of guidelines selected through the HTA website search.8 The International Society for Pharmacoeconomics and Outcomes Research - Society for Medical Decision Making (ISPOR-SMDM) Modeling Good Research Practices Task Force recommend that the conversion of transition probabilities from one cycle length to another should be done through rates. However, no further details are provided.
Discussion
The aim of the targeted review was to identify formal recommendations, such as consensus statements or guidelines, to inform the calculation of transition probabilities for use in Markov models for the economic evaluation of medical interventions. One relevant publication was identified, in which the ISPOR-SMDM Modeling Good Research Practices Task Force recommended that the conversion of transition probabilities from one cycle length to another should be done through rates. However, many key questions around the estimation of TPMs for health care decision-making remain unanswered.
We searched a wide variety of data sources including electronic databases and HTA agency websites to identify relevant studies. However, our approach cannot be considered systematic. Our targeted review might not have captured all studies of interest given that relevant literature in this field is not always formally published as journal articles. Also, our searches of HTA agency websites were limited to ten; so it might be that relevant consensus statements or guidelines are available on unsearched HTA agency websites. Finally, our electronic database searches were limited to English language only, thus potentially leading to language bias and exclusion of relevant articles published in other languages.
This review was limited to modeling methods for medical interventions, and only included formal recommendations such as consensus statements or guidelines; we are aware that a substantial body of literature exists on the topic of estimating TPMs in the financial, engineering, and statistical fields, and from independent authors in the health economics community which would not have been identified by our search protocol.
Therefore, it is recommended that additional research be conducted to consolidate and build on existing knowledge on this topic. An expert panel or working group should be convened to identify key circumstances in which the estimation of transition probabilities is not straightforward, or where the most appropriate approach is considered contentious. A broad systematic review of methodological publications on the topic of TPMs spanning all academic fields should be undertaken, and formal recommendations developed on the basis of the review, and as part of an iterative process amongst the expert panel or working group.
In the absence of consensus statements or guidelines, currently developed Markov models may utilize approaches that reduce accuracy, introduce additional uncertainty, or underestimate the uncertainty that exists. The development of formal guidance on the estimation of TPMs for health care decision-making would allow a more consistent approach to decision-analytic modeling, and therefore to decision-making.
Acknowledgments
We would like to thank Richard Grieve for the critical review of this manuscript and Dave Fox for developing the search strategy. This study was sponsored by Takeda Pharmaceuticals International AG. The abstract of this article was presented as a poster at the International Society for Pharmacoeconomics and Outcomes Research 19th Annual European Congress in 2016. The poster’s abstract has also been published.16
Disclosure
HCS is a permanent employee of Takeda Pharmaceuticals International AG. EO, KKC, EH, and DT have received consulting fees from Takeda Pharmaceuticals International AG. The authors report no other conflicts of interest in this work.
References
Briggs A, Sculpher M. An introduction to Markov Modelling for economic evaluation. Pharmacoeconomics. 1998;13(4):397–409. | ||
Briggs AH, Ades AE, Price MJ. Probabilistic sensitivity analysis for decision trees with multiple branches: use of the Dirichlet distribution in a Bayesian framework. Med Decis Making. 2003;23(4):341–350. | ||
Jackson CH. Multi-state models for panel data: the MSM package for R. J Stat Softw. 2011;38(8):1–29. | ||
Meira-Machado L, Cadarso-Suárez C, de Uña-Alvarez J. Tdc.msm: an R library for the analysis of multi-state survival data. Comput Methods Programs Biomed. 2007;86(2):131–140. | ||
Meira-Machado L, de Uña-Álvarez J, Cadarso-Suárez C, Andersen PK. Multi-state models for the analysis of time-to-event data. Stat Methods Med Res. 2009;18(2):195–222. | ||
Price MJ, Welton NJ, Ades AE. Calculating Markov transition probabilities when treatment effects are reported as relative risks with a different cycle time. Available from: http://www.bristol.ac.uk/social-community-medicine/media/mpes/price-calculating-08.pdf. Accessed July 19, 2016. | ||
Miller DK, Homan SM. Determining transition probabilities: confusion and suggestions. Med Decis Making. 1994;14(1):52–58. | ||
Siebert U, Alagoz O, Bayoumi AM, et al. State-transition modeling: a report of the ISPOR-SMDM modeling good research practices task force-3. Value Health. 2012;15(6):812–820. | ||
Fleurence RL, Hollenbeak CS. Rates and probabilities in economic modelling. Pharmacoeconomics. 2007;25(1):3–6. | ||
Chhatwal J, Jayasuriya S, Elbasha EH. Changing cycle lengths in state-transition models: challenges and solutions. Med Decis Making. 2016;36(8):952–964. | ||
O’Mahony JF, Newall AT, van Rosmalen J. Dealing with time in health economic evaluation: methodological issues and recommendations for practice. Pharmacoeconomics. 2015;33(12):1255–1268. | ||
Taylor DC, Pawar V, Kruzikas D, et al. Methods of model calibration: observations from a mathematical model of cervical cancer. Pharmacoeconomics. 2010; 28 (11):995–1000. | ||
Welton NJ, Ades AE. Estimation of Markov chain transition probabilities and rates from fully and partially observed data: uncertainty propagation, evidence synthesis, and model calibration. Med Decis Making. 2005;25(6):633–645. | ||
Gomes M, Díaz-Ordaz K, Grieve R, Kenward MG. Multiple imputation methods for handling missing data in cost-effectiveness analyses that use data from hierarchical studies an application to cluster randomized trials. Med Decis Making. 2013;33(8):1051–1063. | ||
Rubin DB. An Overview of Multiple Imputation. In: Proceedings of the Survey Research Methods Section of the American Statistical Association. 1988:79–84. Available from: https://www.amstat.org/Sections/Srms/Proceedings/papers/1988_016.pdf. Accessed September 1, 2016. | ||
Olariu E, Cadwell KK, Fox D, et al. Recommendations for the calculation of transition probabilities in Markov cohort models: a targeted literature review. Value in Health. 2016;19(7):A373. |
Supplementary materials
  | Figure S1 Search strategy. |
  | Table S1 Potentially relevant publications identified via the electronic searches |
References
Aalen OO, Borgan O, Fekjaer H. Covariate adjustment of event histories estimated from Markov chains: the additive approach.[Erratum appears in Biometrics. 2003 Jun;59(2):452–453]. Biometrics. 2001;57(4):993–1001. | ||
Alam MF, Barton P, Monahan M. Investigating the impact of structural changes in a NICE single technology appraisal cost-effectiveness model. Value Health. 2015;18(7):A696. | ||
Alarid-Escudero F, Enns E, Peralta-Torres YE, Maclehose R, Kuntz KM. Calibration of piecewise Markov models using a change-point analysis through an iterative convex optimization algorithm. Value Health. 2015;18(7):A814. | ||
Albert PS, Waclawiw MA. A two-state Markov chain for heterogeneous transitional data: a quasi-likelihood approach. Stat Med. 1998;17(13):1481–1493. | ||
Allignol A, Beyersmann J, Gerds T, Latouche A. A competing risks approach for nonparametric estimation of transition probabilities in a non-Markov illness-death model. Lifetime Data Anal. 2014;20(4):495–513. | ||
Andersen PK, Pohar Perme M. Inference for outcome probabilities in multi-state models. Lifetime Data Anal. 2008;14(4):405–431. | ||
Black WC, Nease RF Jr, Welch HG. Determining transition probabilities from mortality rates and autopsy findings. Med Decis Making. 1997;17(1):87–93. | ||
Borgan O. Estimation of covariate-dependent Markov transition probabilities from nested case-control data. Stat Methods Med Res. 2002;11(2):183–202. | ||
Borgan O. Erratum: Estimation of covariate-dependent Markov transition probabilities from nested case-control data. Stat Methods Med Res. 2003;12(2):124. | ||
Boruvka A, Cook RJ. Sieve estimation in a Markov illness-death process under dual censoring. Biostatistics. 2016;17(2):350–363. | ||
Cohen JE. On estimating the equilibrium and transition probabilities of a finite-state Markov chain from the same data. Biometrics. 1968;24(1):185–187. | ||
Cooper NJ, Sutton AJ, Abrams KR, Turner D, Wailoo A. Comprehensive decision analytical modeling in economic evaluation: a Bayesian approach. Health Econ. 2004;13(3):203–226. | ||
Craig BA, Sendi PP. Estimation of the transition matrix of a discrete-time Markov chain. Health Econ. 2002;11(1):33–42. | ||
Dabrowska DM, Ho WT. Confidence bands for comparison of transition probabilities in a Markov chain model. Lifetime Data Anal. 2000;6(1):5–21. | ||
Debosscher A. Unifying stochastic Markov process and its transition probability density function. Phys Rev A. 1991;44(12):7929–7938. | ||
Denton FT, Spencer BG. Modeling the age dynamics of chronic health conditions: life-table-consistent transition probabilities and their application. Can J Aging. 2015;34(2):176–193. | ||
Diaby V, Adunlin G, Montero AJ. Survival modeling for the estimation of transition probabilities in model-based economic evaluations in the absence of individual patient data: a tutorial. Pharmacoeconomics. 2014;32(2):101–108. | ||
Gaveau B, Schulman LS. Multiple phases in stochastic dynamics: geometry and probabilities. Phys Rev E Stat Nonlin Soft Matter Phys. 2006; 73(3 Pt 2):036124. | ||
Gupta S, Bhattacharyya S, Sonathi V, Bakuli A, Mathur AK, Leteneux C. Transition probability estimation using repeated sampling from a fitted mixed model. Value Health. 2014;17(7):A326. | ||
Gupta S, Chattopadhyay S, Gunda P. Generalized implementation of Em algorithm for estimation of transition probability matrix. Value Health. 2015;18(7):A694. | ||
Hawkins DL, Han CP. Estimating transition probabilities from aggregate samples plus partial transition data. Biometrics. 2000;56(3):848–854. | ||
Healy BC, Engler D. Modeling disease-state transition heterogeneity through Bayesian variable selection. Stat Med. 2009;28(9):1353–1368. | ||
Huang GH. Integrated analysis of incidence, progression, regression and disappearance probabilities. BMC Med Res Methodol. 2008; 8:40. | ||
Iacobelli S, Carstensen B. Multiple time scales in multi-state models. Stat Med. 2013;32(30):5315–5327. | ||
Kassteele Jv, Hoogenveen RT, Engelfriet PM, Baal PH, Boshuizen HC. Estimating net transition probabilities from cross-sectional data with application to risk factors in chronic disease modeling. Stat Med. 2012;31(6):533–543. | ||
Kaushik A, Celler BG, Ambikairajah E. A methodology to monitor the changing trends in health status of an elderly person by developing a Markov model. Conf Proc IEEE Eng Med Biol Soc. 2005;2:2171–2174. | ||
Li Z, Pack S. An application of Markov models in estimating transition probabilities for postmenopausal women with osteoporosis. Drug Info J. 2004;38(1):41–46. | ||
Limwattananon C, Limwattananon S. Constructing a state-transition model for an economic evaluation of cancer treatments. J Med Assoc Thai. 2014;97(Suppl 5):S108–S112. | ||
McCombs JS. Pharmacoeconomics: what is it and where is it going?. Am J Hypertens. 1998;11(8 Pt 2):112S–119S; discussion 135S–137S. | ||
Meidani H, Ghanem R. Uncertainty quantification for Markov chain models. Chaos. 2012;22(4):043102. | ||
Meira-Machado L, de Una-Alvarez J, Cadarso-Suarez C. Nonparametric estimation of transition probabilities in a non-Markov illness-death model. Lifetime Data Anal. 2006;12(3):325–344. | ||
Meira-Machado L, de Una-Alvarez J, Cadarso-Suarez C, Andersen PK. Multi-state models for the analysis of time-to-event data. Stat Methods Med Res. 2009;18(2):195–222. | ||
Miller DK, Homan SM. Determining transition probabilities: confusion and suggestions. Med Decis Making. 1994;14(1):52–58. | ||
Milne RJ. Pharmacoeconomic models in disease management. A guide for the novice or the perplexed. Dis Manag Health Outcomes. 1998;4(3):119–134. | ||
Moussa MA, Hathout H, Kasraoui, R, Saleh AK. Measuring the change in contingency tables using Markov models application to the effect of preceding conception on the next one. Methods Inf Med. 1982;21(1):31–33. | ||
Muenz LR, Rubinstein LV. Markov models for covariate dependence of binary sequences. Biometrics. 1985;41(1):91–101. | ||
Nagylaki T. The distribution of sojourn times in finite absorbing Markov chains. Math Biosci. 1976;28(1–2):69–72. | ||
Neine M, Briquet B, Mokdad CE, Vataire AL, Aballea S. Bayesian calibration method to estimate transition probabilities for a Markov model based on a continuous outcome measure: application in Parkinson’s disease. Value Health. 2013;16(7):A325–A326. | ||
Ng ET, Cook RJ. Modeling two-state disease processes with random effects. Lifetime Data Anal. 1997;3(4):315–335. | ||
O’Mahony JF, Newall AT, van Rosmalen J. Dealing with time in health economic evaluation: methodological issues and recommendations for practice. Pharmacoeconomics. 2015;33(12):1255–1268. | ||
Oppe M, Al M, Rutten-van Molken, M. Comparing methods of data synthesis: re-estimating parameters of an existing probabilistic cost-effectiveness model. Pharmacoeconomics. 2011;29(3):239–250. | ||
Paes AT, de Lima AC. A SAS macro for estimating transition probabilities in semiparametric models for recurrent events. Comput Methods Programs Biomed. 2004;75(1):59–65. | ||
Putter H, Fiocco M, Gekus RB. Tutorial in biostatistics: competing risk and multi-state models. Stat Med. 2007;26(11):2389–2430. | ||
Regnier ED, Shechter SM. State-space size considerations for disease-progression models. Stat Med. 2013;32(22):3862–3880. | ||
Rodriguez-Girondo M, de Una-Alvarez J. A nonparametric test for Markovianity in the illness-death model. Stat Med. 2012;31(30):4416–4427. | ||
Rodriguez-Girondo M, de Una-Alvarez J. Testing Markovianity in the three-state progressive model via future-past association. Biom J. 2012;54(2):163–180. | ||
Rodriguez-Girondo M, Una-Alvarez Jd. Methods for testing the Markov condition in the illness-death model: a comparative study. Stat Med. 2016;35(20):3549–3562. | ||
Rosychuk RJ, Sheng X, Stuber JL. Comparison of variance estimation approaches in a two-state Markov model for longitudinal data with misclassification. Stat Med. 2006;25(11):1906–1921. | ||
Rosychuk RJ, Thompson ME. Bias correction of two-state latent Markov process parameter estimates under misclassification. Stat Med. 2003;22(12):2035–2055. | ||
Saint-Pierre P, Combescure C, Daures JP, Godard P. The analysis of asthma control under a Markov assumption with use of covariates. Stat Med. 2003;22(24):3755–3770. | ||
Spitoni C, Verduijn M, Putter H. Estimation and asymptotic theory for transition probabilities in Markov renewal multi-state models. Int J Biostat. 2012;8(1):23. | ||
Tattar PN, Vaman HJ. Testing transition probability matrix of a multi-state model with censored data. Lifetime Data Anal. 2008;14(2):216–230. | ||
Tattar PN, Vaman HJ. The k-sample problem in a multi-state model and testing transition probability matrices. Lifetime Data Anal. 2014;20(3):387–403. | ||
Titman AC. Transition probability estimates for non-Markov multi-state models. Biometrics. 2015;71(4):1034–1041. | ||
Tsang KP, Wang BCM, Garrison L. Estimating Markov chain transition matrices in limited data samples: A Monte Carlo experiment. Value Health. 2012;15(4):A164–A165. | ||
Welton NJ, Ades AE. Estimation of Markov chain transition probabilities and rates from fully and partially observed data: uncertainty propagation, evidence synthesis, and model calibration. Med Decis Making. 2005;25(6):633–645. |
 © 2017 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2017 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
