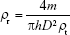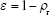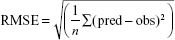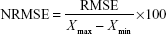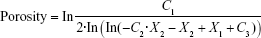Back to Journals » Drug Design, Development and Therapy » Volume 11
Computational intelligence models to predict porosity of tablets using minimum features
Authors Khalid MH, Kazemi P , Perez-Gandarillas L, Michrafy A, Szlęk J, Jachowicz R, Mendyk A
Received 10 August 2016
Accepted for publication 15 September 2016
Published 12 January 2017 Volume 2017:11 Pages 193—202
DOI https://doi.org/10.2147/DDDT.S119432
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Georgios Panos
Mohammad Hassan Khalid,1 Pezhman Kazemi,1 Lucia Perez-Gandarillas,2 Abderrahim Michrafy,2 Jakub Szlęk,1 Renata Jachowicz,1 Aleksander Mendyk1
1Department of Pharmaceutical Technology and Biopharmaceutics, Faculty of Pharmacy, Jagiellonian University Medical College, Krakow, Poland; 2Centre National de la Recherche Scientifique, Centre RAPSODEE, Mines Albi, Université de Toulouse, Albi, France
Abstract: The effects of different formulations and manufacturing process conditions on the physical properties of a solid dosage form are of importance to the pharmaceutical industry. It is vital to have in-depth understanding of the material properties and governing parameters of its processes in response to different formulations. Understanding the mentioned aspects will allow tighter control of the process, leading to implementation of quality-by-design (QbD) practices. Computational intelligence (CI) offers an opportunity to create empirical models that can be used to describe the system and predict future outcomes in silico. CI models can help explore the behavior of input parameters, unlocking deeper understanding of the system. This research endeavor presents CI models to predict the porosity of tablets created by roll-compacted binary mixtures, which were milled and compacted under systematically varying conditions. CI models were created using tree-based methods, artificial neural networks (ANNs), and symbolic regression trained on an experimental data set and screened using root-mean-square error (RMSE) scores. The experimental data were composed of proportion of microcrystalline cellulose (MCC) (in percentage), granule size fraction (in micrometers), and die compaction force (in kilonewtons) as inputs and porosity as an output. The resulting models show impressive generalization ability, with ANNs (normalized root-mean-square error [NRMSE] =1%) and symbolic regression (NRMSE =4%) as the best-performing methods, also exhibiting reliable predictive behavior when presented with a challenging external validation data set (best achieved symbolic regression: NRMSE =3%). Symbolic regression demonstrates the transition from the black box modeling paradigm to more transparent predictive models. Predictive performance and feature selection behavior of CI models hints at the most important variables within this factor space.
Keywords: computational intelligence, artificial neural network, symbolic regression, feature selection, die compaction, porosity
Introduction
Pharmaceutical companies rely on solid dosage forms, which constitute a majority of the total manufactured and marketed product. Powder characteristics, manufacturing process parameters, and various other tangible entities have profound effects on the quality of a solid dosage form in a complex way. The quality of a solid dosage form, among other factors, can be assessed based on its hardness and porosity, which can be used as indirect measurements of its capability and rate to dissolve.1 In most cases, the complexity of relationships among the possible material parameters and upstream processes diminishes the understanding of the system as a whole.
Porosity, known as the ratio of volume of void space to the bulk volume and generally represented as a percentage, is an important property that controls the microstructure of the tablet during compression. It can assist in the understanding of the dispersion mechanism, behavior after ingestion, moisture penetration, and with certain prerequisites, even bioavailability. Porosity measurements are also known to be relevant indicators of drug stability.2 The effect of shape and porosity of granules has been studied by Johansson and Alderborn,3 suggesting that stronger tablets are formed when granules with irregular porosity are compressed. Theoretically, the porosity of a tablet can be a predictor of its dissolution behavior as well.4
Previous works on this topic have revealed that porosity influences tablet strength; lactose tablets with larger pores were weak5–7 and similar relationships were observed with other excipients such as glucose and mannitol.7,8 The importance of porosity as an indirect measurement of dissolution was demonstrated using rate of water uptake, and solvent penetration was studied in microcrystalline cellulose (MCC) tablets with different porosities. Results showed that tablets with 10% and 15% porosity take up water much faster (30 s) and expand by up to 50% of original thickness, while tablets with 5% porosity are much slower in water uptake behavior (148 s), in addition to showing less expansion.9 The correlation of porosity with die compaction force has been well studied in the past.10,11 It was explained that tablets made from pharmaceutical powders do not exhibit the quasi-exponential trend proposed by Heckel12 for evolution of porosity against pressure. Pharmaceutical powders exhibit plastic deformation properties, while Heckel’s model works well with metallic powders.11 Tablet brittleness has been described as an exponential growth function of porosity using a diverse set of pharmaceutical tablets by Gong et al.13
Data-driven empirical models established using computational intelligence (CI) methods can be used as surrogates to run in silico experiments to predict porosity. Use of CI offers reduction in experiments, leading to cost and time savings and broader understanding of the system. CI tools have been used in works addressing the pharmaceutical industry’s various problems, including tensile strength, porosity, and dissolution problems.14–18
Generally, modeling and simulation (M-and-S) is a huge area of science, in which various paradigms of modeling are used, mostly based on well-established theory. In pharmaceutical sciences, a broad area of molecular modeling, using ab initio techniques such as molecular docking offers profound examples of such an approach.19–21 However, when no such theory is present, only empirical modeling is a suitable alternative, in particular with data-driven modeling in focus.
The aim of this work is to create data-driven intelligent models using well-known and established approaches to compute the porosity of tablets based on average granule size, proportion of MCC, and die compaction force. Furthermore, it aims to show that CI models can be represented in the form of an equation as a result of modeling through symbolic regression – a shift from the black box paradigm to transparency. Last, this work attempts to dissect CI models to ascertain which of the input variables are more important to predict porosity. The models are based on experimental data generated by Perez-Gandarillas et al.22
Materials and methods
Ethics
Since this study is conducted purely in silico, no ethics review was sought or granted here.
Training data
The experimental data set contains records of binary tablets made from MCC and lactose. Powder mixtures were roll compacted under constant conditions. Ribbons were milled to produce granules of three different size ranges (315–500; 630–800, and 800–1,000 μm). In continuation of the process, the feed powders (binary mixtures) and their granules from each size range were die compacted using six different die compaction forces. The experiments were done in triplicates.22
The tablets were characterized through the porosity. Therefore, the porosity is an outcome (Table 1A). After ejection, the tablet dimensions (diameter and thickness) were measured with a digital micrometer (Mitutoyo, Takatsu-ku, Japan), and tablet mass was weighed with an electronic balance (CP224S). These data were used to calculate the relative density (ρr) of each tablet, as follows:
  | Table 1 Characteristics of MCC tablets and the various compaction conditions |
|
|
where m is the mass, h is the tablet thickness, D is the tablet diameter, and ρt is the true density of each binary mixture.
Once the relative density is obtained, the porosity (ε) is calculated as follows:
|
|
Validation data
An additional data set from single-powder tableting experiments was used to validate the CI models. The data set is explained in Perez-Gandarillas et al.23 The validation set is composed of data generated by varying roll compaction over two sets of tooling (cheek plates and sealed rim rolls) and two roll compaction forces (4 kN/cm and 8 kN/cm). The ribbons were milled under constant settings and granules were compacted under seven different die compaction forces (Table 1B). Variation in roll compactor tooling and roll compaction/die compaction forces introduces a challenge to trained CI models.
Model training
The models were built using three different approaches:
- Tree-based predictive models
- Artificial neural networks (ANNs) (monmlp)
- Symbolic regression (rgp).
i.Decision trees (Cubist)
ii.Random forests (randomForest)
Extensive combinations of algorithm parameters in all the approaches were tried. The data set was divided into 10 folds, where nine of the folds were used for training and one for testing. Tenfold cross-validation (10cv) is a renowned method to create a “real-world” depiction of a problem from the data representing it.24 Models were selected based on their RMSE values calculated according to Equation 1. The RMSE values are a measure of the differences between the predicted and the observed values and are completely independent of the modeling technique. Hence, they are reliable and widely accepted measures for evaluating a model. R statistical environment was used to create the models.
|
|
where “pred” is the predicted value from the models, “obs” is the observed value from the experiments, and “n” is the total number of test cases.
The RMSE values were normalized using Equation 2.
|
|
where RMSE was calculated in Equation 1, Xmax and Xmin are the highest and the lowest observed values for the outcome in the data set, respectively.
CI methods
Decision trees – Cubist
Cubist is a tree-based modeling approach wherein a linear model is fit iteratively, resulting in a set of linear models at each node starting from the root to the last node of the tree. Cubist is an ensemble-based technique. All variables that are covered by a linear function at a single node are then discarded from the future iterations for that particular tree. This process is recursively continued until all the input variables have been covered by a single or a set of rules in a tree. This is also known as the separate-and-conquer approach. At every step, the response of the model is analyzed and adjusted to be used by the next model, until the final model is achieved. The final prediction is a simple average of the predictions from each tree in the ensemble.25
Random forest
Random forests are well known tree-based models. One model is shaped by numerous trees in the collection. Independent trees are generated based on sample data randomly taken out of the training data set. Errors exhibited by individual trees are collectively representative of the generalization error of the randomForest model.26 An extensive search for the best architecture was carried out using a 10cv scheme, followed by training of the best-performing architecture on the full data set.
ANNs – monmlp
Monmlp is the implementation of ANN in R. ANNs with monmlp are generalized feed-forward ANNs that work in a monotone fashion using the backpropagation (BP) algorithm enhanced by the nonlinear minimization algorithm (nlm) for training. Neural networks imitate the structure of the human brain, whereby information is passed on between neurons in the form of synapses. Monmlp allows two hidden layers of neurons, with hyperbolic tangent and linear activation as transfer functions.27 In monmlp, signals move forward from the input layer through sigmoid neurons before reaching the linear output layer.
Neurons in each layer consist of N inputs (Xi), which multiplies by the proper generated weight element (Wi,j) for the layer named j. Summation of the weighted inputs plus bias (bj) produces the input (nj) for the activation function, using which the output of each neuron (yi) can be calculated.
Moreover, different activation functions, such as hyperbolic tangent sigmoid (TAN-SIG) transfer function, logarithm sigmoid (LOGSIG) transfer function, and pure linear (PURELIN) transfer function, are the potential transfer functions that can be used in each layer.28 The neural network package monmlp was run extensively to find the best-performing network architecture with 10cv. The whole data set was used to retrain the model on the best architecture.
Symbolic regression by rgp
Genetic programming (GP) is a bioinspired algorithm based on evolution principles to solve complex problems. A complex problem is broken down into smaller, simpler problems with random solutions. These solutions are then evolved through the biologically mimicked process of variation and selection until the end condition is reached or a workable solution is generated. Thus, rgp is an implementation of GP methods in the R environment.29 Package rgp results are simple representations of the problem without being exposed to a priori information. rgp offers various options for initialization, variation, and selection procedures inherent in GP. GP implements a tree structure representation to show the mathematical equations. The tree structure is composed of two parts: function set (nodes) and a terminal set (leaves).30 The function set can be chosen through the operators {+, −, *, /, sin, cos, log, abs}, mathematical functions, conditional statements, or even the user-defined operators. In addition, the terminal set includes constants and model variables.31,32
To find the best solution, different runs were conducted by iterating over GP tuning parameters. The most important tuning parameters are maximum size of the chromosome, the number of generations, and population size.30 The size of the chromosome, which governs the maximum length of the equation, was varied from 5 to 100. The population size was set to 1,000, and the number of generations was set to 500 million evolution steps divided into 100 stages.
These equations can be optimized by different strategies.33,34 For this experiment, equations were created on the whole data set, and then selected ones were optimized using the simulated annealing (SANN) algorithm, followed by a quasi-Newton (Broyden–Fletcher–Goldfarb–Shanno [BFGS]) method.35,36
Independent feature selection by fscaret
The package fscaret allows semiautomatic feature selection, working as a wrapper for the caret package in R. Fscaret is specialized for in silico feature selection experiments, whereby approximately 120 different packages are used to fit models.37 Input feature ranking is extracted from trained models by using weighted averages. Sum of squared errors (SSE), mean squared errors (MSEs), and RMSEs are used to evaluate models. fscaret has been successfully implemented in recent studies.38,39
Results and discussion
Approximately 10,000 models with different architectures were developed using the CI methods mentioned herein. External validation of the models was done using a data set on tableting with MCC under different roll compaction conditions.
Model performance
Results for best models from all the different CI methods are shown in Table 2. All CI methods perform well on the data sets. The multiple linear regression (MLR) model, shown in Table 3, does not represent the process adequately (15% error), suggesting that nonlinearity needs to be addressed with a robust method. Figure 1 shows the predicted vs observed graph for the MLR model. Hence, to find a suitable model, decision trees, ANNs, and GP algorithms were used. RGP was performed as an early-stage experiment at this point. Nonetheless, RGP shows results comparable to those from other methods, which is evidence that evolutionary computational methods are quite robust and can fit complex data well.
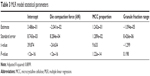  | Table 3 MLR model statistical parameters |
  | Figure 1 Predicted vs observed graph for MLR. |
ANN model
ANNs show best 10cv generalization results among all the experiments conducted, although they fail to maintain the performance on the external data set. A simple network of two hidden layers of 13 and 11 nodes, respectively, with 10 ensembles and 100 iterations was found out to be the best-performing architecture. Hyperbolic tangent was used as the transfer function within the ANN (Figure 2).
  | Figure 2 Predicted vs observed graph for ANN. |
Recent works39,40 demonstrate the ANN as a much coveted CI modeling tool. ANNs show plausible results in supervised learning, a behavior that can be attributed to the high generalization ability of the ANNs. Moreover, 10cv ANN models exhibit a meager 1% normalized root-mean-square error (NRMSE) (Table 1). Although ANNs are robust, are widely used, and have great generalization capabilities, they are generally black-box models. The resulting ANN models cannot be dissected with certainty to establish how different input features are interacting with each other to predict porosity. Furthermore, ANN models are unstable where retraining could lead to a slightly different understanding of the system. The source of instability and inconsistency lies within the design and strategy used to train an ANN. Weights in the ANN are generated at random to expedite the learning process while the process of learning itself is deterministic. Hence, the randomness introduced while generating the weights could lead to a completely different model after retraining.
Symbolic regression
GP is a stable, a transparent method that can offer structural insights into the models. Symbolic regression exhibits a good model fit (4% 10cv error, 3% external). The advantage of symbolic regression is that the result can be represented in the form of a mathematical formula.41 The model for porosity can be represented as in Equation 4. A regression plot is shown in Figure 3.
  | Figure 3 Predicted vs observed graph for rgp (NRMSE: 4%). |
The model represents the outcome of porosity with high accuracy (4% 10cv error).
|
|
where C1 =1.52888, C2 =2.415892, C3 =7.28763, X1 is the die compaction force (in kilonewtons), and X2 is the MCC proportion (as fraction).
External validation
Data from additional tableting experiments was used to test the trained models. Tablets were made with MCC. The external data set was particularly challenging for the models because roll compaction conditions were kept constant in the training data set while being systematically changed in the external data set. Table 1 shows the results of external validation. The models were able to predict porosity with substantial accuracy using unseen input data. The external data set is composed of experiments with two different roll compactor tooling (cheek plates and rim rolls) and two different roll compaction forces (4 kN and 8 kN) for each. The variety of roll compactor settings introduces variance in the external data set unknown to the trained models. Although CI systems are not known for their extrapolation abilities,42 the models presented herein are able to extrapolate successfully in a small range. Regardless of the complexity in the external data set, the rgp model represented by Equation 4 makes accurate predictions of the test cases from all different tooling and force conditions (Figure 4). Table 4 shows the levels of accuracy of prediction for the external validation data set. Non-roll-compacted powder is predicted with the most accuracy (NRMSE: 7%), followed by prediction of roll compaction using rim rolls at 4 kN (NRMSE: 9%).
  | Table 4 RMSE and NRMSE for external validation data set using rgp model |
  | Figure 4 Model performance on external data set. |
Model description
Further analysis of trained CI models gives interesting insights into the governing parameters within this tableting experiment.
Feature selection by GP
Symbolic regression model exhibits feature selection behavior. The resulting model represents two inputs in the equation as compared to the original three inputs presented to it while training. Feature selection process discards the input variables which are not contributing decisively toward the outcome; in this case, the average granule fraction size. Considering granule fraction range as a disposable input characteristic for the outcome of porosity is contrary to previous works,43 but justified within the range of this training data set.22 A comparison between the GP model and the ANN model shows that the average granule fraction size does not exercise significant effect on the outcome (Figure 5), also supported by MLR (Table 3). ANN model does not perform feature selection on its own and is bound to use all three inputs in the final model. Therefore, GP model discarding the average granule fraction size makes it less complex and improves performance on the external data set (Table 2).
  | Figure 5 Surface plot showing the influence of average granule fraction size on porosity based on the monmlp model. |
Further RSM analysis based on the GP equation shows that variation in the amount of MCC does not have a profound effect on the porosity of the tablet, while an increase in the die compaction force considerably reduces the porosity of tablets (Figure 6), a behavior that can be attributed to particle rearrangement followed by plastic deformation during the compression stage.44
  | Figure 6 Surface plot showing the influence of MCC and die compaction force on porosity based on rgp model. |
Feature selection on the external data set to establish the surplus of discarded variables
Plausible performance of the trained CI models on a significantly different external data set could be an occurrence of chance. To study this in detail, important features from both the data sets were compared. Feature selection experiments using fscaret were run independently on the external data set. Confirmatory models were developed with a variation of input vectors using the tree-based learning method Cubist. The resulting top features of the external data set are in agreement with the features used to train the models. The results confirm that the die compaction force is the most important variable, with roll compaction force, roll compaction tooling, percentage of material in the formulation, and granule fraction range displaying much lower ranking. Models developed without the information of roll compaction force, roll compaction tooling, and granule fraction range predict porosity of tablets accurately (Table 5: experiments with two and three inputs). The successful modeling shows that these variables do not contribute to the outcome within this design space. The results strongly suggest redundancies in the original data set, which, once removed, do not affect the prediction of porosity within the factor space. Correlation analysis of the original data set reveals that porosity is highly correlated to die compaction force (Figure 7).
  | Figure 7 Correlation plots for (A) training and (B) test data. |
Conclusion
CI models for MCC-based tablets are presented herein. The models have been rigorously tested internally using 10cv and then externally validated by using a challenging data set. The models exhibit reliable prediction behavior, with the best achieved 10cv-NRMSE of 1% on using ANNs. The models also exhibit understanding of the tableting process within the design space. The equation for porosity is presented as the result of symbolic regression models with 10cv-NRMSE of 4% and external validation NRMSE of 3%. Presentation of CI models in the form of an equation makes them transparent to scrutiny and shows how the input variables interact with each other plus contribute toward the specific outcome of porosity. Contrary to common knowledge, roll compaction parameters such as tooling and compression force do not influence the porosity of tablets. Such conclusions are confined to the local design space and cannot be treated as general rules governing the tableting process.
Acknowledgments
This work was supported by the IPROCOM Marie Curie Initial Training Network, funded through the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme FP7/2007–2013/under REA grant agreement number 316555.
Disclosure
The authors report no conflicts of interest in this work.
References
Hattori Y, Otsuka M. NIR spectroscopic study of the dissolution process in pharmaceutical tablets. Vib Spectrosc. 2011;57(2):275–281. | ||
Gucluyildiz H, Banker GS, Peck GE. Determination of porosity and pore-size distribution of aspirin tablets relevant to drug stability. J Pharm Sci. 1977;66(3):407–414. | ||
Johansson B, Alderborn G. The effect of shape and porosity on the compression behaviour and tablet forming ability of granular materials formed from microcrystalline cellulose. Eur J Pharm Biopharm. 2001;52(3):347–357. | ||
de Oliveira JM Jr, Andreo Filho N, Chaud MV, Angiolucci T, Aranha N, Martins AC. Porosity measurement of solid pharmaceutical dosage forms by gamma-ray transmission. Appl Radiat Isot. 2010;68(12):2223–2228. | ||
Riepma KA, Vromans H, Zuurman K, Lerk CF. The effect of dry granulation on the consolidation and compaction of crystalline lactose. Int J Pharm. 1993;97(1–3):29–38. | ||
Zuurman K, Riepma KA, Bolhuis GK, Vromans H, Lerk CF. The relationship between bulk density and compactibility of lactose granulations. Int J Pharm. 1994;102(1–3):1–9. | ||
Juppo AM. Relationship between breaking force and pore structure of lactose, glucose and mannitol tablets. Int J Pharm. 1995;127(1):95–102. | ||
Westermarck S, Juppo AM, Kervinen L, Yliruusi J. Pore structure and surface area of mannitol powder, granules and tablets determined with mercury porosimetry and nitrogen adsorption. Eur J Pharm Biopharm. 1998;46(1):61–68. | ||
Yassin S, Goodwin DJ, Anderson A, et al. The disintegration process in microcrystalline cellulose based tablets, part 1: influence of temperature, porosity and superdisintegrants. J Pharm Sci. 2015;104(10):3440–3450. | ||
Çelik M. Overview of compaction data analysis techniques. Drug Dev Ind Pharm. 1992;18(6&7):767–810. | ||
Masteau JC, Thomas G. Modelling to understand porosity and specific surface area changes during tabletting. J Chem Phys. 1999;101(3):240–248. | ||
Heckel RW. Density-pressure relationship in powder compaction. Trans Metall Soc AIME. 1961;221:671–675. | ||
Gong X, Chang SY, Osei-Yeboah F, et al. Dependence of tablet brittleness on tensile strength and porosity. Int J Pharm. 2015;493(1–2):208–213. | ||
Bourquin J, Schmidli H, van Hoogevest P, Leuenberger H. Comparison of artificial neural networks (ANN) with classsical modelling techniques using different experimental designs and data from a galenical study on a solid dosage form. Eur J Pharm Sci. 1998;6(4):287–301. | ||
Shao Q, Rowe RC, York P. Comparison of neurofuzzy logic and decision trees in discovering knowledge from experimental data of an immediate release tablet formulation. Eur J Pharm Sci. 2007;31(2):129–136. | ||
Landin M, Rowe RC, York P. Advantages of neurofuzzy logic against conventional experimental design and statistical analysis in studying and developing direct compression formulations. Eur J Pharm Sci. 2009;38(4):325–331. | ||
Mendyk A, Tuszynski PK, Khalid MH, Jachowicz R, Polak S. How-to: empirical IVIVR without intravenous data. Dissolution Technol. 2015;22(2):12–18. | ||
Khalid MH, Tuszyński PK, Kazemi P, Szlek J, Jachowicz R, Mendyk A. Transparent computational intelligence models for pharmaceutical tableting process. Complex Adapt Syst Model. 2016;4:7. | ||
Yu C, Brian S. Molecular docking and ligand specificity in fragment-based inhibitor discovery. Nat Chem Biol. 2009;5:358–364. | ||
Chan DS, Yang H, Kwan MH, et al. Structure-based optimization of FDA-approved drug methylene blue as a c-myc G-quadruplex DNA stabilizer. Biochimie. 2011;93(6):1055–1064. | ||
Deimel P, Bababrik R, Wang B. Direct quantitative identification of the “surface trans-effect”. Chem Sci. 2016;7:5647–5656. | ||
Perez-Gandarillas L, Mazor A, Souriou D, Lecoq O, Michrafy A. Compaction behaviour of dry granulated binary mixtures. Powder Technol. 2015;285:62–67. | ||
Perez-Gandarillas L, Perez-Gago A, Mazor A, Kleinebudde P, Lecoq O, Michrafy A. Effect of roll-compaction and milling conditions on granules and tablet properties. Eur J Pharm Biopharm. 2016;106:38–49. | ||
Lachenbruch PA, Mickey MR. Estimation of error rates in discriminant analysis. Technometrics. 1968;10(1):1–12. | ||
Quinlan JR. Learning with continuous classes. In: Proceedings of the 5th Australian Joint Conference on Artificial Intelligence; 1992; Hobart, TAS: World Scientific Pub Co Inc. | ||
Breiman L. Random forests. Mach Learn. 2001;45:5–32. | ||
Cannon AJ [webpage on the Internet]. monmlp: Monotone multi-layer perceptron neural network; 2012. R package version 1.1.2. Available from: http://CRAN.R-project.org/package=monmlp. Accessed October 27, 2016. | ||
Di Nicola D, Pierantozzi M. Surface tension of alcohols: a scaled equation and an artificial neural network. Fluid Phase Equilib. 2015;389:16–27. | ||
Rsymbolic Project. Cologne University of Applied Sciences. C2010-13. Available from: https://cran.r-project.org/web/packages/rgp/vignettes/rgp_introduction.pdf. Accessed October 27, 2016. | ||
Koza JR. Genetic programming as a means for programming computers by natural selection. Stat Comput. 1994;4:87–112. | ||
Sette S, Boullart L. Genetic programming: principles and applications. Eng Appl Artif Intell. 2001;14:727–736. | ||
Kazemi P, Khalid MH, Szlek J, et al. Computational intelligence modeling of granule size distribution for oscillating milling. Powder Technol. 2016;301:1252–1258. | ||
Poli R, Langdon WB, McPhee NF [webpage on the Internet]. A Field Guide to Genetic Programming. 2008. Available from: http://www.gp-field-guide.org.uk. Accessed July 9, 2016. | ||
Nash JC, Varadhan R. Unifying optimization algorithms to aid software system users: optmix for R. J Stat Softw. 2011;43(9):1–14. | ||
Nash JC. On best practice optimization methods in R. J Stat Softw. 2014;60(2):1–14. | ||
Szlek J, Paclawski A, Lau R, Jachowicz R, Mendyk A. Heuristic modeling of macromolecule release from PLGA microspheres. Int J Nanomedicine. 2013;8(1):4601–4611. | ||
Pacławski A, Szlęk J, Lau R, Jachowicz R, Mendyk A. Empirical modeling of the fine particle fraction for carrier-based pulmonary delivery formulations. Int J Nanomedicine. 2015;10:801–810. | ||
Gonzales GB, Smagghe G, Coelus S, et al. Collision cross section prediction of deprotonated phenolics in a travelling-wave ion mobility spectrometer using molecular descriptors and chemometrics. Anal Chim Acta. 2016;924:68–76. | ||
Mansa RF, Bridson RH, Greenwood RW, Barker H, Seville JPK. Using intelligent software to predict the effects of formulation and processing parameters on roller compaction. Powder Technol. 2008;181:217–225. | ||
Kachrimanis K, Karamyan V, Malamataris S. Artificial neural networks (ANNs) and modeling of powder flow. Int J Pharm. 2003;250(1):13–23. | ||
Khalid MH, Tuszynski PK, Kazemi P, Szlek J, Jachowicz R, Mendyk A. Transparent computational intelligence models for pharmaceutical tableting process. Complex Adapt Syst Model. 2016;4:7. | ||
Sovany T, Papos K, Kasa P Jr, Ilic I, Srcic S, Pintye-Hodi K. Application of physicochemical properties and process parameters in the development of a neural network model for prediction of tablet characteristics. AAPS PharmSciTech. 2013;14(2):511–516. | ||
Eichie FE, Kudehinbu AO. Effect of particle size of granules on some mechanical properties of paracetamol tablets. Afr J Biotechnol. 2009;8(21):5913–5916. | ||
Martin CL, Bouvard D, Shima S. Study of particle rearrangement during powder compaction by the discrete element method. J Mech Phys Solids. 2003;51(4):667–693. |
 © 2017 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2017 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.