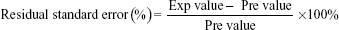Back to Journals » International Journal of Nanomedicine » Volume 9 » Issue 1
Comparison of process parameter optimization using different designs in nanoemulsion-based formulation for transdermal delivery of fullerene
Authors Ngan CL, Basri M, Lye FF, Fard Masoumi HR, Tripathy M, Karjiban RA, Abdul-Malek E
Received 8 April 2014
Accepted for publication 24 May 2014
Published 15 September 2014 Volume 2014:9(1) Pages 4375—4386
DOI https://doi.org/10.2147/IJN.S65689
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Cheng Loong Ngan,1 Mahiran Basri,1,2 Fui Fang Lye,1 Hamid Reza Fard Masoumi,1 Minaketan Tripathy,3,4 Roghayeh Abedi Karjiban,1 Emilia Abdul-Malek1
1Department of Chemistry, Faculty of Science, 2Halal Products Research Institute, Universiti Putra Malaysia, Selangor, Malaysia; 3Laboratory of Fundamentals of Pharmaceutics, Faculty of Pharmacy, Puncak Alam Campus, Universiti Teknologi MARA, Selangor, Malaysia; 4Brain and Neuroscience Communities of Research, Universiti Teknologi MARA, Selangor, Malaysia
Abstract: This research aims to formulate and to optimize a nanoemulsion-based formulation containing fullerene, an antioxidant, stabilized by a low amount of mixed surfactants using high shear and the ultrasonic emulsification method for transdermal delivery. Process parameters optimization of fullerene nanoemulsions was done by employing response surface methodology, which involved statistical multivariate analysis. Optimization of independent variables was investigated using experimental design based on Box–Behnken design and central composite rotatable design. An investigation on the effect of the homogenization rate (4,000–5,000 rpm), sonication amplitude (20%–60%), and sonication time (30–150 seconds) on the particle size, ζ-potential, and viscosity of the colloidal systems was conducted. Under the optimum conditions, the central composite rotatable design model suggested the response variables for particle size, ζ-potential, and viscosity of the fullerene nanoemulsion were 152.5 nm, –52.6 mV, and 44.6 pascal seconds, respectively. In contrast, the Box–Behnken design model proposed that preparation under the optimum condition would produce nanoemulsion with particle size, ζ-potential, and viscosity of 148.5 nm, –55.2 mV, and 39.9 pascal seconds, respectively. The suggested process parameters to obtain optimum formulation by both models yielded actual response values similar to the predicted values with residual standard error of <2%. The optimum formulation showed more elastic and solid-like characteristics due to the existence of a large linear viscoelastic region.
Keywords: nanoemulsion, palm kernel oil ester, fullerene, central composite rotatable design, Box–Behnken design, response surface methodology
Introduction
Fullerene (C60), the third member in the carbon allotrope line-up, is a truncated icosahedron sp2-hybridized carbon molecule with 30 carbon–carbon double bonds (C=C). It is widely known for its capability in scavenging free radicals through multiple addition reactions that occur momentarily in the presence of radicals.1,2 In the past couple of years, researchers have been actively exploiting fullerene due to its excellent antioxidant activity. This brings promising medicinal benefits as a remedy or therapy in various health illnesses, such as cancer, neurodegenerative disorders, allergies, and many more.3–5 Another advantage is that pristine fullerene is nontoxic to a large variety of living organisms, including human.6 Furthermore, there is an immense interest to further employ fullerene in the cosmetic and cosmeceutical industries as an antioxidant.7–9
Despite its vast advantages, fullerene is insoluble in water, which makes it more challenging to incorporate into pharmaceutical and cosmetic products. Hence, efforts to modify the surface of the molecules into functionalized fullerene have been reported.10 However, engineered fullerene derivatives can be highly toxic.6 An alternative route of application was identified where oil was used as a biocompatible carrier for fullerene.11
To improve the solubility and bioavailability of fullerene, a suitable carrier system comprised of oil should be developed. Wax esters emerge as the key ingredient in cosmeceutical industries, due to their excellent wetting behavior at interfaces and a nongreasy feeling upon application on the skin surfaces.12,13 This offers a potential solution to formulate an emulsion system to deliver fullerene in an effective way.
Nanotechnology has been explored due to its potential to revolutionize the cosmetic and cosmeceutical industries. Nanoemulsion-based cosmeceuticals have improved efficacy; whereby, the active ingredient will have better skin penetration and a higher rate in successful drug delivery to the target site due to its small particle size. Besides, the long-term colloidal stability of nanoemulsions can be achieved through high ζ-potential due to the increase of the repulsive force between droplets. Nanoemulsion is a nonequilibrium colloidal system where oil phase is dispersed as fine droplets, usually with particle size from 20–200 nm, throughout the aqueous phase stabilized by surfactants.14 Nanoemulsions can be prepared by high-energy emulsification or by low-energy emulsification methods.15 However, nanoemulsions are thermodynamically unstable colloidal systems that are highly dependent on their physicochemical properties, usually based on the preparation method.14 Thus, a precise preparation method is necessary to avoid overprocessing, which will be a waste of time and cost. Process parameters that involved the controlling of the energy input of homogenizers and process time could be a deciding point to acquire ideal characteristics. However, combinations of emulsification methods are often applied, and an investigation on each influence individually (the univariate approach) can be a tedious task.
These process variables influence the outcome of the responses in different manner where interaction between variables may even occur. Response surface methodology (RSM) is a powerful statistical tool that executes effectively in a multivariate way to study the relationships between independent and response variables. Based on mathematical principles, the optimization of certain processes can be achieved easily by setting the desirable parameters. Moreover, the minimum number of experimental runs will be conducted to fully assess the effect of independent variables and their interactions between variables on the selected responses.16
The aim of this study was to investigate the influence of process parameters – homogenization rate, sonication amplitude, and sonication time – on the physicochemical properties (particle size, ζ-potential, and viscosity) of fullerene nanoemulsions using RSM with two different designs. The comparison between Box–Behnken design (BBD) and central composite rotatable design (CCRD) was analyzed for the purpose of optimizing the condition to obtain desirable responses, such as small particle size and high ζ-potential. Fullerene solubilized in palm kernel oil esters was used to formulate an oil-in-water nanoemulsion system. An amplitude sweep test was carried out on the optimum formulations to find out the rheological characteristics that can be correlated with the nanoemulsions stability.
Materials and methods
Materials
Fullerene, with a purity of 99.5%, was purchased from Sigma-Aldrich (St Louis, MO, USA). Nonionic surfactants, polyoxyethylene sorbitan monooleate (T80), viscous liquid, and sorbitan monooleate (S80) were from Sigma-Aldrich. Xanthan gum from Xanthomonas campestris and white beeswax, bleached, were obtained from Sigma-Aldrich. Phenonip, preservative, was purchased from Bramble Berry (Bellingham, WA, USA). Palm kernel oil esters (PKOEs) were synthesized in our laboratory through the enzymatic transesterification of palm kernel oil and oleyl alcohol using Lipozyme RM IM as the catalyst.13 Deionized water was purified using the Milli-Q water system (EMD Millipore, Billerica, MA, USA).
Fullerene nanoemulsions preparation
Formulations containing fullerene were prepared using a combination of high-energy emulsification techniques – high shear homogenization and ultrasonic dispersion. Fullerene was fully dissolved in PKOEs (160 μg/g) using a magnetic stirrer. The oil phase, which was composed of fullerene, 12.5% (weight/weight [w/w]) PKOEs, 1.0% (w/w) beeswax, and 0.7% (w/w) phenonip, and the aqueous phase, 7.7% (w/w) T80:S80 (4:1), 0.9% (w/w) xanthan gum, and deionized water, was stirred separately while heating at 75.0°C to dissolve all the ingredients completely. Phenonip was added into the formulations as an antimicrobial agent. Fullerene nanoemulsions (100 g) were prepared by adding an aqueous phase slowly into the oil phase while homogenized using Polytron high shear homogenizer (PT3100; Kinematica AG, Lucerne, Switzerland) at room temperature (25.0°C±2°C) for 15 minutes. The premixed emulsions were further subjected to ultrasonic dispersion by 24 kHz ultrasonic tip processor (UP400S; Hielscher Ultrasonics GmbH, Teltow, Germany) with a maximum power output of 400 W. The titanium probe tip of 14 mm diameter and 100 mm length was submerged into the emulsions while sonicated at specific amplitude (alternating on–off every 1 second). Samples were immersed in an ice bath to mitigate the ultrasound thermal effect. High shear homogenization rate, sonication amplitude, and time were varied, according to the experimental design.
Particle size and ζ-potential determination
The particle size and ζ-potential were determined using a dynamic light scattering droplet size analyzer (Malvern Zetasizer Nano ZS90; Malvern Instruments, Malvern, UK) equipped with an argon laser (λ =488 nm). The measurement was performed with an angle of 173° at room temperature (25.0°C±0.5°C). The samples were diluted (1:200) with deionized water to avoid multiple scattering effects. Then, they were filled into the zeta disposable cells. The diluted fullerene nanoemulsions were filled into the capillary cell, using the 3 mL syringe to avoid the presence of air bubbles before inserted into the module. For optimization measurement, the instrument was equilibrated for 120 seconds to the acquired stable temperature. For data analysis, each sample was analyzed twice after 24 hours of sample preparation; each analysis consisting of five replicates and the measurements were reported as average for each analysis.
Viscosity measurement
The viscosity of colloidal systems was measured using a dynamic shear rheometer (Kinexus Rotational Rheometer; Malvern Instruments, Malvern, UK) at a fixed shear rate of 0.1 seconds−1 at 298 K. The measurements were performed within 24 hours after sample preparation using cone and plate geometry (4°/40 mm), the gap being set at 0.15 mm. Samples were loaded and left for 5 minutes to equilibrate, before carrying out the measurement. The viscosity of each sample was recorded in pascal seconds (Pa⋅s) at an interval of 5 seconds until 60 data points were generated, and the average viscosity value was calculated.
Rheological characterization
Oscillatory strain sweep analysis was run on the optimum formulation at different strain amplitudes from 1%–1,000% using the dynamic shear rheometer. The rheometer was equipped with cone and plate geometry (4°/40 mm). Measurements were performed at 25.0°C±0.1°C. Dynamic oscillatory experiments were done to identify the storage (elastic) (G′) and the loss (viscous) modulus (G″) at a fixed frequency of 1 Hz to acquire a linear viscoelastic region (LVR). This region is referring to the region where the G′ is independent of applied shear stress up to the critical strain value (γc). This test is able to analyze the viscoelasticity of a specific microscopic architectural material.
Experimental design
RSM was employed to study the process parameters of the independent variables: homogenization rate (X1); sonication amplitude (X2); and sonication time (X3), on the particle size (Y1), ζ-potential (Y2), and viscosity (Y3) of the nanoemulsions. The experiments were approached using two different designs as a comparison between the CCRD and BBD. The coded independent variables in both of the designs are shown in Table 1. The total number of runs was generated by Design Expert version 6.0.6 by Stat-Ease Inc. (Minneapolis, MN, USA). The design matrix was created, and the results were statistically analyzed, which were then converted into a response surface.
  | Table 1 Coded independent variables used in RSM design |
The designs were evaluated separately based on the influence of process variables in the modeling of the emulsion particle size, ζ-potential, and viscosity. Each design was expressed by second-order polynomial regression equation to generate the model shown below,
Yi = β0 + β1X1 + β2X2 + β3X3 + β11X12 + β22X22 + β33X32 + β12X1X2 + β13X1X3 + β23X2X3 | (1) |
Design Expert software was used to obtain the combination of values that illustrate the response surface model. Experiments were run in a randomized order to avoid questionable variability that affects the outcome of the response due to extraneous factors. The center of the experimental field was performed six and five times for CCRD and BBD, respectively.
Statistical analysis
The analysis of variance (ANOVA) was performed to determine the significant differences between the independent variables. A reduced model involves statistically significant independent variables (P<0.05), which it takes into account. The three-dimensional (3D) surface response and contour plots were constructed to represent the interaction between independent variables and responses. Multiple regressions were applied in analyzing experimental data to predict the coefficients of the fitted second-order polynomial model.
Verification of models
Eight random formulations were prepared to validate the models. Experimental values were compared with the predicted values to check the adequacy of the final reduced models. Recommended optimum process parameters were also performed to verify the optimum response values predicted by the model. Percentage of residual standard error (RSE %) was calculated for each response.
Results and discussion
Model fitting
The particle size, ζ-potential, and viscosity of the fullerene nanoemulsions obtained from the experimental design using CCRD and BBD are given in Table 2. Coefficients of the polynomial equation were calculated using experimental values, and the equation was used in the prediction of the response values of the nanoemulsions. The predicted values derived from both designs were consistent with the experimental value. Final reduced models for particle size could be represented by the quadratic polynomial equations suggested using ANOVA as shown below,
CCRD: Y1 = 152.27 − 3.27 X1 − 5.76 X2 − 12.17 X3 + 6.42 X22 + 2.99 X1X3 - 4.56 X2X3 | (2) |
BBD: Y1 = 153.09 − 3.74 X1 − 4.11 X2 − 12.15 X3 + 5.35 X22 + 3.60 X1X3 - 3.85 X2X3 | (3) |
The ANOVA of the resultant quadratic polynomial models for the particle size of fullerene nanoemulsions is shown in Table 3. The significance of the regression coefficients was represented by the P-value for a polynomial equation. The smaller P-value indicates higher significance of the corresponding coefficients. The linear term of sonication time (P<0.0001) had the largest effect on the particle size, followed by the quadric term of sonication amplitude (P<0.0001) and linear term of homogenization rate (P<0.0001). The interactive effect between the sonication amplitude and time (P<0.05), as well as the interactive effect between the homogenization rate and sonication time (P<0.05) exhibited a significant effect on the particle size of nanoemulsions. The remaining three interactive effect terms (homogenization rate and sonication amplitude, and the quadric terms of homogenization rate and sonication time) did not show any influence to the particle size of nanoemulsions. Hence, the insignificant terms were excluded in the final models. Lack of fit value (CCRD =2.19; BBD =1.97) was insignificant, which points to the fact that pure errors such as the experimental error were at their minimum.
While the response for ζ-potential, ANOVA suggested that the quadratic polynomial equations best described the CCRD and BBD. All linear and quadric terms have a significant effect on ζ-potential of the colloidal system with P-value less than 0.05. The final reduced quadratic models for both experimental designs were demonstrated in the following equations in terms of coded factor.
CCRD: Y1 = −53.67 − 2.45 X1 − 2.10 X2 − 5.74 X3 + 1.97 X12 + 2.75 X22 − 1.18 X32 + 1.38 X1X3 − 1.87 X2X3 | (4) |
BBD: Y1 = −53.70 − 2.65 X1 − 2.34 X2 − 5.89 X3 + 1.66 X12 + 2.69 X22 − 1.51 X32 + 1.60 X1X3 − 1.97 X2X3 | (5) |
The ANOVA results and regression analysis were used to fit the models related to ζ-potential with the process parameters (Table 3). Quadratic polynomial models with large F-value and small P-value indicate substantial significance of the models with a confidence level of 95%. The interaction between the homogenization rate with sonication amplitude and time shows a significant effect on the ζ-potential (P<0.05). Despite the interaction effect between different variables, the linear term of sonication time imposes the largest effect on the ζ-potential with the highest F-value (P<0.0001). Since the interactive term between homogenization rate and sonication amplitude gave an insignificant effect, it was excluded from the quadratic polynomial model. The P-value of lack of fit from both models was nonsignificant, indicating minimal pure errors which affirmed the fitness of the model.
For both experimental design of CCRD and BBD, linear interaction was suggested by showing the relationship between the three independent variables and the viscosity of the system. None of the interactive term was observed in this particular case on the viscosity of the fullerene nanoemulsions. Linear polynomial equation was selected, showing each term was highly significant toward the viscosity as shown here,
CCRD: Y1 = 44.12 − 3.16 X1 − 9.03 X2 − 13.35 X3 | (6) |
BBD: Y1 = 44.73 − 2.75 X1 − 8.41 X2 − 13.76 X3 | (7) |
The linear term of sonication time (P<0.0001) stood out from the rest of the terms, showing the highest F-value followed by sonication amplitude (P<0.0001) and homogenization rate (P<0.05). This indicated that sonication time has the largest effect on influencing the outcome of the nanoemulsions’ viscosity. No significant interaction effect between the variables was found in this event. Low lack of fit values (CCRD =2.97; BBD =2.99) implied the models were insignificant, relative to pure error caused during the experiment.
The approximated regression coefficients describing the effect of independent variables were often related to standard deviation, prediction error sum of squares (PRESS), R2, predicted R2, adjusted R2, and adequate precession. Regression coefficients of the final reduced quadratic polynomial models are tabulated in Table 4. The coefficients of determination (R2) for particle size, ζ-potential, and viscosity extracted using ANOVA were 0.9765, 0.9734, and 0.9569 for CCRD; whereas, they were 0.9625, 0.9736, and 0.9281 for BBD, respectively. The analysis showed that the viscosity has the highest coefficient value, followed by particle size and ζ-potential. The R2 value from CCRD showed a higher value compared to BBD, but both designs fitted well into the second-order polynomial model.
  | Table 4 Regression coefficients of the final reduced models |
Response surfaces analysis
When the experimental data gathered from the responses of process parameters for both designs was analyzed, ANOVA showed a quadratic polynomial equation was best to predict the particle size and ζ-potential of the nanoemulsion. This showed that there was a significant effect in the interaction between independent variables, which was indicated by a large F-value and a small P-value of interaction terms. However, the viscosity of the nanoemulsion showed that the linear polynomial equation was best fitted for all variables involved, and interaction terms were not significant in the model.
To better illustrate the effect of independent variables on the particle size and ζ-potential, the 3D surface response model graphs and contour plots of the quadratic polynomial models are shown in Figures 1 and 2. The 3D plots showed that increasing the sonication amplitude and homogenization rate led to a reduction in the particle size of the nanoemulsion. It was attributed to higher shear force or disruption mechanism applied, which breaks the oil droplets into a smaller size.17 Higher sonication time favored the formation of nanoemulsions with smaller particle size. It was due to the longer duration for the action of ultrasonic radiation forces to disperse the emulsion droplets into smaller sizes.
However, this trend was reversed after the particle reached its minimum size at the amplitude of 52%. This suggested that there was an optimum level for attaining the maximum effect from acoustic emulsification.18 Hence, there was no further reduction of particle size when the maximum dispersity was reached at the given acoustic power density. Another observation was witnessed where the effect was described as an overprocessing event, which was caused by the increase of coalescence in oil droplets at higher shear rate.19,20 Increase in sonication amplitude would increase the ultrasonic radiation forces that drove the oil droplets to the anodes and antinodes of the acoustic field. Nearby droplets that were close to each other would coalesce and lead to overprocessing.21 In addition, the turbulence generated at the vicinity of the probe tip at higher operating amplitude increase the rate of collision between the droplets, causing the production of acoustic bubbles. These bubbles were collected at the nodes of the acoustic field, due to the increase of the ultrasonic radiation forces. The remainder of the emulsions were shielded from the effect of acoustic oscillations by the bubble cloud and coalesced to form larger emulsion droplets.22
The absolute value of ζ-potential increased in the higher homogenization rate, due to the higher shear force applied that could disrupt the interfacial forces that hold the particle together and overcome Laplace pressure.23 Increase of sonication amplitude had a similar effect on the ζ-potential of the colloidal system. However, there was no further increase in the absolute value of ζ-potential at sonication amplitude greater than 54%, where the particle has the smallest size. This observation could be explained by the overprocessing effect where the droplets had reached the maximum dispersity.23 Changes in the ζ-potential will depend on the electrophoretic mobility of the dispersed particle, due to the effect of homogenization process in the nanoemulsion preparation. Hence, the electrophoretic mobility of small particle size is greater and eventually leads to higher ζ-potential. In addition, the application of higher sonication amplitude would cause cavitation-induced thermal effect, resulting in the deterioration of T80:S80. Miscibility and solubility of the surfactant might be altered.24 At a constant concentration of T80:S80, the deterioration of the mixed-surfactant lowered the amount of surfactant to adsorb on the newly formed droplet interface. Depletion interaction between the dispersed particles increased and rendered the colloidal system to be unstable.
Generally, higher sonication time favored the formation of nanoemulsions. The interaction between sonication amplitude and time has a negative effect on ζ-potential of the nanoemulsions. Increase in sonication time caused a rising in the temperature of the system. The cavitation-induced thermal effect caused by an increase of both sonication amplitude and time contributed to the overprocessing and the instability of the colloidal system. The temperature rise could cause the number of cavitation nuclei as well as their vapor pressure to increase. A damping of shock waves was produced, lowering the maximum pressure reached at the implosion sites.25 The emulsifying efficiency was affected by this limitation, leading to a decrease in the absolute value of ζ-potential. It was observed that the emulsion that had been sonicated at amplitude 70%, and emulsion that had undergone sonication for 150 seconds was separated into two phases after 1 week. This observation is corroborated with the cavitation-induced thermal effect on the ζ-potential.
The linear polynomial equations can be best described for all the independent variables where they have negative effect on the viscosity of the nanoemulsions. Viscosity of the emulsions decreased as the high shear homogenization rate and sonication amplitude increased. The change of viscosity as the function of shear rate indicated that the nanoemulsions were non-Newtonian fluids. Before the application of shear force using the high shear homogenizer, the coarse emulsions were aggregates of droplets. As the shear rate increased, the increasing hydrodynamic forces were able to deform and disrupt the flocs leading to a reduction in viscosity.26
On the other hand, higher sonication amplitude led to the formation of highly unstable bubbles that collapsed within a few milliseconds. The hydrocolloid dispersion particles were exposed to high shear forces around the bubble cloud. These high shear forces together with the thermal effect induced by sonication caused the cleavage of macromolecules of xanthan gum. The OH radicals formed in the cleavage of polysaccharides, resulting in broken glycosidic linkages, leading to a decrease in viscosity.27 As the sonication time increased, the apparent viscosity of the nanoemulsions decreased, due to the expedited depolymerization of xanthan gum. The interactions between the polymer molecules were weakened, and this destruction of the polymer network resulted in a decrease of viscosity.28
Optimization of conditions for formulating fullerene nanoemulsions
Fullerene nanoemulsion with desired characteristics, such as a small particle size and high absolute value of ζ-potential, can be considered as the optimum formulation. Despite wanting these characteristics to be achieved, a cost-effective and fast preparation should not be compromised if expanded into a large scale. The lowest energy input in producing fullerene nanoemulsions was chosen to reduce the cost of production, and the possibility of overprocessing can be avoided. In addition, production time could be cut down when sonication time is reduced.
Under the optimum conditions, the process parameters involving a homogenization rate of 4,352 rpm and sonication amplitude of 48% for 97 seconds yielded a predicted response value for the particle size, ζ-potential, and viscosity were estimated to be 152.5 nm, −52.6 mV, and 44.6 Pa⋅s for CCRD; whereas, the optimum conditions suggested by BBD was a homogenization rate at 4,354 rpm and sonication amplitude of 49% for 105 seconds that would produce nanoemulsion with the particle size, ζ-potential, and viscosity of 148.5 nm, −55.2 mV, and 39.9 Pa⋅s, respectively. Both designs predicted almost similar responses to each other; thus, this affirmed the reliability of the optimum formulation toward the desirable criteria. Formulations were also prepared under the recommended optimum conditions, and the resulting responses were compared to the predicted values for both models.
Verification of the models
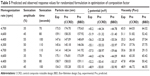
The verification of final models was completed to test the adequacy of the predicted response values by performing eight additional randomized formulations, as shown in Table 5. No significant difference between the actual and predicted values was shown in the results that indicated excellent fitness of the models generated.
Comparison of CCRD and BBD models in optimum conditions
Comparison between two experimental designs in obtaining optimum formulations using suggested process conditions by CCRD and BBD were conducted. The responses of three independent variables (homogenization rate, sonication amplitude, and sonication time) are shown in Table 6. Given the stated conditions, the extracted results were correlated with the predicted outcome and RSE was computed as shown below,
| (8) |
The result showed that CCRD produced a lower RSE value than the BBD for all variables, which suggested that CCRD is able to predict more accurate data compared to the actual experiment (Table 6). This indicates that CCRD is a better design comparing to BBD in this case.
Rheological characterization
Optimum formulations suggested by CCRD and BBD were run through oscillatory strain sweep test, and the results were shown in Figure 3. G′ and G″ were constant at low deformation, which indicated the sample structure was uninterrupted. Once the plateau started to decrease, this marked the end of LVR, due to the breakdown of architecture within the colloidal system. From the LVR, both formulations displayed higher G′ value (storage modulus) compared to G″ value (loss modulus) indicating that the systems exhibited elastic behavior rather than viscous behavior.29 The results showed that both formulations generated wide LVR that directly related to high rigidity of the system. Samples with wide LVR indicated excellent stability against phase separation as well.29 Optimum formulations were found to be monophasic even when they were left for 90 days at room temperature (25.0°C±0.5°C) and 45°C in the incubator DK-S1020 (DAIKI Sciences Co. Ltd, Seoul City, Korea). The LVR of the optimized formulation from CCRD and BBD have a similar complex shear strain of 31.57%. The yield stress of formulation was determined at the end of LVR, where an optimum formulation was 8.76 Pa. The phase angle was 16.4°, which was lower than 45.0°, indicating that the sample was solid-like material.
  | Figure 3 Storage modulus (G′), loss modulus (G″), and phase angle (δ) as a function of strain amplitude γ of the optimum fullerene nanoemulsion. |
Conclusion
Control of process parameters in the fullerene nanoemulsion preparation is crucial to acquire desirable attributes for effective transdermal delivery. The fullerene nanoemulsion was prepared by employing high shear and ultrasonic emulsification methods while further optimized by CCRD and BBD as multivariate modeling tools in process parameter studies for improved accuracy and quality in results. Significant interaction between the process parameters was observed in determining the particle size and ζ-potential (P<0.05), except viscosity where no interaction between process parameters can be observed. Both final reduced models predicted the same polynomial model, which validates one another in achieving the optimum process conditions. However, CCRD (RSE <1.2%) displayed a better performance in model fitting and estimation of actual values than BBD (RSE <2.0%). Optimum nanoemulsion exhibited wide LVR giving great resistance against flow while maintaining the structure of the nanoemulsion itself, indicating excellent long-term stability. Therefore, the development of fullerene nanoemulsion by ultilizing multivariate statistical technique can be cost-effective and able to achieve desirable properties suitable for transdermal application in the same time.
Acknowledgments
The authors would like to thank the Ministry of Higher Education, Malaysia for the financial support under the Fundamental Research Grant Scheme (FRGS) (02-01-13-1235FR) and MyBrain15.
Disclosure
The authors report no conflicts of interest in this work.
References
Hirsch A, Brettreich M. Fullerene: Chemistry and Reactions. Weinheim: Wiley-VCH Verlag GmbH & Co; 2005. | ||
Krusic PJ, Wasserman E, Keizer PN, Morton JR, Preston KF. Radical reactions of c60. Science. 1991;254(5035):1183–1185. | ||
Haley B, Frenkel E. Nanoparticles for drug delivery in cancer treatment. Urol Oncol. 2008;26(1):57–64. | ||
Dugan LL, Lovett EG, Quick KL, Lotharius J, Lin TT, O’Malley KL. Fullerene-based antioxidants and neurodegenerative disorders. Parkinsonism Relat Disord. 2001;7(3):243–246. | ||
Ryan JJ, Bateman HR, Stover A, et al. Fullerene nanomaterials inhibit the allergic response. J Immunol. 2007;179(1):665–672. | ||
Kolosnjaj J, Szwarc H, Moussa F. Toxicity studies of fullerenes and derivatives. Adv Exp Med Biol. 2007;620:168–180. | ||
Inui S, Aoshima H, Nishiyama A, Itami S. Improvement of acne vulgaris by topical fullerene application: unique impact on skin care. Nanomedicine. 2011;7(2):238–241. | ||
Lens M. Recent progresses in application of fullerenes in cosmetics. Recent Pat Biotechnol. 2011;5(2):67–73. | ||
Kato S, Taira H, Aoshima H, Saitoh Y, Miwa N. Clinical evaluation of fullerene-C60 dissolved in squalane for anti-wrinkle cosmetics. J Nanosci Nanotechnol. 2010;10(10):6769–6774. | ||
Bosi S, Da Ros T, Spalluto G, Prato M. Fullerene derivatives: an attractive tool for biological applications. Eur J Med Chem. 2003; 38(11–12):913–923. | ||
Cataldo F. Solubility of fullerenes in fatty acids esters: a new way to deliver in vivo fullerenes. Theoretical calculations and experimental results. In: Cataldo F, Da Ros, T, editors. Medicinal Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotubes (Carbon Materials: Chemistry and Physics). Berlin: Springer Science; 2008:317–335. | ||
Mat Hadzir N, Basri M, Abdul Rahman MB, Salleh AB, Raja Abdul Rahman RN, Basri H. Phase behaviour and formation of fatty acid esters nanoemulsions containing piroxicam. AAPS Pharm Sci Tech. 2013;14(1):456–463. | ||
Keng PS, Basri M, Zakaria MRS, et al. Newly synthesized palm esters for cosmetic industry. Ind Crops Prod. 2009;29(1):37–44. | ||
Gutiérrez JM, González C, Maestro A, Solè I, Pey CM, Nolla J. Nano-emulsions: new applications and optimization of their preparation. Curr Opin Colloid Interface Sci. 2008;13(4):245–251. | ||
Rezaee M, Basri M, Rahman RN, Salleh AB, Chaibakhsh N, Karjiban RA. Formulation development and optimization of palm kernel oil esters-based nanoemulsions containing sodium diclofenac. Int J Nanomedicine. 2014;9:539–548. | ||
Hao J, Fang X, Zhou Y, et al. Development and optimization of solid lipid nanoparticle formulation for ophthalmic delivery of chloramphenicol using a Box-Behnken design. Int J Nanomedicine. 2011; 6:683–692. | ||
Li PH, Chiang BH. Process optimization and stability of D-limonene-in-water nanoemulsions prepared by ultrasonic emulsification using response surface methodology. Ultrason Sonochem. 2012; 19(1):192–197. | ||
Mason TJ. Large scale sonochemical processing: aspiration and actuality. Ultrason Sonochem. 2000;7(4):145–149. | ||
Jafari SM, Assadpoor E, He Y, Bhandari B. Re-coalescence of emulsion droplets during high-energy emulsification. Food Hydrocoll. 2008;22(7) 1191–1202. | ||
Desrumaux A, Marcand J. Formation of sunflower oil emulsions stabilized by whey proteins with high-pressure homogenization (up to 350 MPa): effect of pressure on emulsion characteristics. Int J Food Sci Tech. 2002;37(3):263-269. | ||
Pangu GD, Feke DL. Acoustically aided separation of oil droplets from aqueous emulsions. Chem Eng Sci. 2004;59(15):3183–3193. | ||
Kentish S, Wooster TJ, Ashokkumar M, Balachandran S, Mawson R, Simons L. The use of ultrasonics for nanoemulsion preparation. Innovative Food Science and Emerging Technologies. 2008;9(2):170–175. | ||
Cheong JN, Tan CP, Man YBC, Misran M. α-Tocopherol nanodispersions: Preparation, characterization and stability evaluation. J Food Eng. 2008;89(2):204–209. | ||
Tang SY, Manickam S, Wei TK, Nashiru B. Formulation development and optimization of a novel Cremophore EL-based nanoemulsion using ultrasound cavitation. Ultrason Sonochem. 2012;19(2):330–345. | ||
Canselier JP, Delmas H, Wilhelm AM, Abismail B. Ultrasound Emulsification – An Overview. J Dispers Sci Technol. 2002;23(1–3): 333–349. | ||
Floury J, Desrumaux A, Lardières J. Effect of high-pressure homogenization on droplet size distributions and rheological properties of model oil-in-water emulsions. Innovative Food Science and Emerging Technologies. 2000;1(2):127–134. | ||
Tiwari BK, Muthukumarappan K, O’Donnel CP, Cullen PJ. Rheological properties of sonicated guar, xanthan and pectin dispersions. Int J Food Prop. 2010;13:223–233. | ||
Karaman S, Yilmaz MT, Ertugay MF, Baslar M, Kayacier A. Effect of ultrasound treatment on steady and dynamic shear properties of glucomannan based salep dispersions: optimization of amplitude level, sonication time and temperature using response surface methodology. Ultrason Sonochem. 2012;19(4):928–938. | ||
Lippacher A, Müller RH, Mäder K. Liquid and semisolid SLN dispersions for topical application: rheological characterization. Eur J Pharm Biopharm. 2004;58(3):561–567. |
 © 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2014 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.