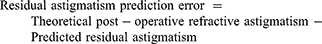Comparison of Barrett and Emmetropia Verifying Optical Toric Calculators

Introduction

Nearly 60% of eyes have clinically significant astigmatism ≥ 0.75 D.¹ As such, when cataract surgery is anticipated, correction of this refractive error with a toric intraocular lens (IOL) is often part of the surgical plan. Historically, surgeons based astigmatism correction on anterior corneal astigmatism measurements. However, it is now well established that pre-operative planning should include use of a modern toric calculator that takes into account the effect of posterior corneal astigmatism.²

The Barrett Toric Calculator (BTC) is widely regarded as one of the most accurate IOL power calculation formulas for use with toric IOLs.³ The Emmetropia Verifying Optical (EVO) v2.0 Toric Calculator is a newer, thick-lens, vergence-based formula that takes into account the optical dimensions of the eye and different IOL geometries.⁴ The calculators are similar in that they both link effective toricity of the IOL to effective lens position (ELP). A recent study by Kane and Connell reported that the performance of the BTC and EVO calculators did not differ significantly from one another.⁵ However, this data was based upon a single toric IOL platform and came from a single surgeon. The purpose of this study was to compare the performance of the BTC and EVO v2.0 Toric Calculators with respect to astigmatism prediction accuracy, using data from a multi-center clinical trial on an IOL platform designed to correct lower levels of astigmatism.

Methods

This was a secondary analysis of data from a prospective clinical trial in which eyes with clinically significant astigmatism were implanted with a single-piece hydrophobic acrylic neutral-aspheric toric IOL (enVista Toric MX60T, Bausch & Lomb, Bridgewater, NJ). The original study design, including description of pre-surgical and surgical technique have been previously described.⁶ The original study was approved by a central Institutional Review Board (The IRB Company, Buena Park, CA). The Penn State College of Medicine IRB deems the secondary analysis of de-identified data to be non-human subjects research; as such, the present study was exempt from IRB approval. Best practices for comparison of calculator performance were followed,⁷ which included use of post-operative biometry to derive the predicted post-operative residual astigmatism for each eye using each of the two calculators. Using post-operative biometry is one way to fully account for the effect of surgically induced astigmatism.

One of the challenges of comparing toric calculator performance lies in the fact that the two calculators will often recommend slightly different implantation axes, and this needs to be taken into account in the analysis. To do this, we used a “remove and replace” method recommended by Warren Hill.⁸ This is done by mathematically adding the astigmatism induced by the toric IOL at its actual axis of alignment to the manifest refraction and then subtracting the same at the calculator’s recommended axis (equation 1) to derive a new theoretical post-operative refractive astigmatism value. It is also an oversimplification to assume that each step size of a toric IOL (ie, MX60T125, MX60T200, etc) contributes a fixed amount of astigmatism correction to each eye. Instead, the effective toricity is linked to ELP. To account for this, the effective toricity of the implanted IOL in each eye was deduced through extrapolation. For example, if the BTC calculator predicts residual astigmatism of 0.25 D @ 90 with an MX60T125 and 0.23 D @ 180 with an MX60T200, one can conclude an effective toricity of 0.48 D for every 0.75 D of astigmatism at the IOL plane, for that eye. As such, an MX60T200 would induce 1.28 D of astigmatism at its actual axis of alignment.

(Equation #1)

Predicted residual astigmatism values from the two calculators were converted to the spectacle plane. Residual astigmatism prediction error was calculated for each eye and for each calculator by subtracting the predicted residual astigmatism from the theoretical post-operative refractive astigmatism (Equation #2). This was done by converting the theoretical and predicted astigmatism vectors to Cartesian coordinates and then subtracting the corresponding x- and y-components, as described by Holladay.⁹ The paired x- and y-differences were then converted back to polar coordinates to create the clinically meaningful residual astigmatism prediction error vector. Outcome measures of interest included the arithmetic and vector (centroid) means of the residual astigmatism prediction error, proportion of eyes with a residual astigmatism prediction error less than 0.5 or 1.0 diopters (D), and proportion of eyes in which the theoretical post-operative refractive astigmatism matched the predicted residual astigmatism with respect to orientation [against-the rule (ATR), oblique, or with-the-rule (WTR)]. ATR astigmatism is defined as having axis oriented within 30 degrees of the 0–180 meridian, and WTR astigmatism was defined as having an axis oriented within 30 degrees of 90.

(Equation #2)

Statistical analysis was performed using SAS Software v9.4 (SAS Institute Inc., Cary, NC). Arithmetic mean residual astigmatism prediction error magnitudes from the two calculators were compared using repeated measures ANOVA. The residual astigmatism prediction error centroids from the two calculators were compared using the Hotelling’s T-squared test.¹⁰ Proportions were compared using generalized estimating equation methodology.¹¹ Results were considered significant at p ≤ 0.05.

Results

The multi-centered clinical trial from which the dataset was derived was conducted across 9 clinical sites and included 10 surgeons. The dataset included 165 eyes from 165 patients that received an MX60T IOL. Fifty-five of these eyes were excluded from the present analysis due to missing data points, which included white-to-white or lens thickness values. One additional eye was excluded due to a large discrepancy between the target spherical equivalent (SE) and the BTC and EVO SE predictions (data validation error). Thus, the analysis was based on 109 eyes from 109 patients. The demographics of these eyes are displayed in Table 1. The distribution of pre-operative corneal astigmatism and post-operative refractive astigmatism within the study population is also displayed in Figure 1. Due to inclusion and exclusion criteria from the original clinical trial, the dataset included only 5 eyes with mean keratometry values < 41 or > 47, and 8 eyes with axial lengths < 22 or > 25.2. Thus, one limitation of the present analysis is that there are insufficient eyes with extreme biometric values upon which to evaluate the performance of the BTC and EVO calculators for these sub-groups. The magnitude of the anterior corneal astigmatism was not normally distributed but instead concentrated towards lower magnitudes, as would be expected in a random sampling of the population. Sixty-seven (61.5%), 38 (34.9%), and 4 (3.7%) eyes had their anterior corneal astigmatism oriented against-the-rule, with-the-rule, and oblique, respectively. Of eyes that received a toric IOL, 79 (72.5%) received a MX60T125, 18 (16.5%) received an MX60T200, and 12 (11%) received a MX60T275. These lenses have cylinder powers of 1.25, 2.0 and 2.75 D at the IOL plane and contribute approximately 0.9, 1.40, and 1.93 D of astigmatism correction at the corneal plane, respectively.

Table 1 Demographics

Figure 1 Double angle plots depicting the pre-operative corneal astigmatism and post-operative refractive astigmatism for the study population implanted with toric intraocular lenses.

Figure 2 depicts double-angle plots showing the astigmatism prediction error for each eye for the two calculators. The arithmetic mean residual astigmatism prediction errors were 0.59 ± 0.38 D and 0.59 ± 0.36 for the BTC and EVO calculators, respectively (p = 0.98). The residual astigmatism prediction error centroids were 0.18 D @ 89° ± 0.66 D and 0.20 D @ 89° ± 0.66 D, respectively (p = 0.21). The proportion of eyes with a residual astigmatism prediction error ≤ 0.5 D was 50% for BTC and 46% for EVO (p = 0.28). The proportion of eyes with a residual astigmatism prediction error ≤ 1.0 D was 86.2% (94/109) for BTC and 87.2% (95/109) for EVO (p = 0.56). The proportion of eyes in which the calculator’s predicted orientation of astigmatism matched the theoretical post-operative refractive astigmatism was 81% for BTC and 77% for EVO (p = 0.15).

Figure 2 Double angle plots depicting the residual astigmatism predictor error for each eye with the (A) Barrett and (B) Emmetropia Verifying Optical (EVO) v2.0 Toric Calculators.

There were 15 eyes in which the residual astigmatism prediction error was greater than 1.0 D with the BTC. Eleven and four of these eyes had ATR and WTR preoperative corneal astigmatism, respectively. For 13 of these 15 eyes, EVO also produced a prediction error greater than 1.0 D. Of the 14 eyes in which the residual astigmatism prediction error was greater than 1.0 D with EVO, 10 and 4 had ATR and WTR preoperative corneal astigmatism, respectively. For 13 of these 14 eyes, BTC also produced a prediction error greater than 1.0 D. In short, there was a slight predilection toward large residual astigmatism prediction errors in ATR eyes for both calculators.

Discussion

Our group previously published a study comparing the legacy enVista and EVO v2.0 toric calculators, and concluded that EVO was superior.¹² The former analysis was run on the exact same dataset as in the present study, however the arithmetic and vector residual astigmatism prediction errors reported for the EVO v2.0 toric calculator in the two studies are slightly different, and this demands an explanation. In the previous work, the arithmetic and vector residual astigmatism prediction errors were 0.57 ± 0.38 D and 0.17 @ 90 ± 0.67 D, respectively; in the present study, they were 0.59 ± 0.36 D and 0.20 @ 89 ± 0.66 D. The reason for this slight difference is because the former study did not link effective toricity of the IOL to ELP, but instead assumed a fixed contribution of astigmatism for each model toric IOL (ie, MX60T125, MX60T200, MX60T275), irrespective of eye geometry. Thus, we believe the analysis in the present study to be more sophisticated.

The results of the present study are comparable to findings from previous literature. In a 2015 study by Abulafia et al, use of the BTC resulted in a centroid residual astigmatism prediction error of 0.02 D.¹³ Another study published in 2016 by Abulafia et al found centroid residual astigmatism prediction errors of 0.05 and 0.04 D after applying the Abulafia-Koch formula to two toric calculators that only took into account anterior corneal astigmatism.² In a third study by Kane and Connell,⁵ the mean arithmetic and centroid residual astigmatism prediction errors were 0.51 and 0.10 @ 111 ± 0.63 D, respectively, for the BTC calculator and 0.51 and 0.16 @ 100 ± 0.62 D, respectively, for EVO v2.0. Note that in all three of these previous works, error values and standard deviations were slightly less than in the present study. One plausible explanation for this might be that all of these datasets were derived from a single surgeon, thus the intraoperative and post-operative protocols might have been more consistent than those applied across the multi-center clinical trial from which the present dataset was derived.

Conclusions

The present study confirms that the BTC and EVO Toric Calculators are remarkably similar in their prediction of residual astigmatism after toric IOL placement. The strengths of this study include the fact that data were derived from a multi-center clinical trial (making the results more generalizable than from a single surgeon) and that best practices for data analysis were followed. This included using one eye from each patient, post-operative biometry and actual IOL alignment. Using these inputs means this is a theoretical (as opposed to real-world) analysis, but is also the purest judge of a calculator’s performance. The present study also has several limitations, which include the fact that 55 eyes from the original dataset were excluded from the analysis due to unmeasured LT and WTW values. We chose to do this because it is likely to be the most applicable to current practice, since biometers in use today (as opposed to 2013–2016 when the dataset was collected) routinely collect these parameters. It also created a uniform dataset that allowed the two calculators to operate optimally. An even larger sample might have allowed us to look for differences in the calculators’ performance with respect to against-the-rule, oblique, or with-the-rule astigmatism sub-groups. Last, the dataset included lower powered toric IOLs only. Evaluation with a dataset that includes higher powered torics would have allowed us to compare the two calculators’ performance in those with higher levels of pre-operative astigmatism.