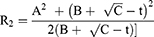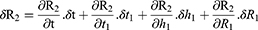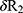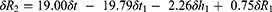Spotlight on the Corneal Back Surface Astigmatism: A Review

Introduction

The classical texts identified the corneal back surface as being a relatively inert intra-ocular optical boundary that had a negligible impact on the overall optical performance of the eye.^1,2 Nevertheless, since 2000 there has been a resurgence of interest in the curvature, and in particular the astigmatism, of the corneal back surface. A quick check on “PubMed” leads to more than 200 hits after typing in “corneal posterior surface power.” Changes in corneal back surface astigmatism are expected after most forms of keratoplasty,^3–5 in cases of keratoconus,^3,6–8 Fuchs’ endothelial corneal dystrophy,^8,9 and during refractive therapies including orthokeratology.¹⁰ In addition, corneal back surface astigmatism is claimed to impact on the performance of the eye in relation to refractive surgery^11,12 and planning for cataract surgery especially in astigmatic eyes.^13–25 Some investigators reported that corneal back surface astigmatism remains stable after refractive surgery, and this would have a marginal impact on later routine phacoemulsification.^26–32 This is certainly not the case in patients that underwent more invasive procedures, such as radial keratotomy, where profound changes in corneal back surface astigmatism can occur.^33–35 Thus, it is reasonable to expect corneal back surface astigmatism to impact on refraction, and IOL power selection when such extraordinary cases request cataract surgery.

Current Approaches for the Assessment of Back Corneal Astigmatism

Total corneal astigmatism is modified by routine phacoemulsification and this alteration appears to be driven by the change in corneal back surface astigmatism on an individual case-by-case basis.³⁶ But, to what extent does corneal back surface astigmatism vary within a typical sample drawn from a normal population? Table 1 lists the mean corneal back surface astigmatic power values reported in some of the key publications on this topic. The earliest publication reported a mean (±s.d.) corneal back surface astigmatic power value of 0.41(±0.03)D.³⁷ The lowest, highest and typical mean values are 0.18(±0.03)D,³⁸ 1.04(±0.20)D,³⁹ and 0.26 (±0.15)D,⁴⁰ respectively. Most reported mean values were small, verging on the insignificant, but the range of values can be >0.75D.^22,41–43 The difference between the lowest and highest means is about 6.5 times greater when compared with the typical average ±s.d value. Corneal back surface astigmatism cannot be measured directly. It is an estimate based on other measurements and assumptions. The lack of cohesion between these studies could be due to genuine differences between population samples or systematic differences in the way values for the corneal back surface astigmatism are derived.

Table 1 Key Previous Estimates of Corneal Back Surface Astigmatism

The current crop of automated systems designed to provide values of corneal back surface astigmatism estimate the radius of curvature at multiple locations over the corneal back surface. Full descriptions of the more widely available systems can be found in a range of review articles and numerous websites.^44–48 These radii are converted into power values, using the standard lens surface formula, assuming the refractive indices of the cornea and aqueous humour are 1.376 and 1.336, respectively. When the orthogonal radii of the corneal back surface are 5.8mm and 6.8mm the corresponding respective powers are −6.90D and −5.88D. Ray tracing through classical model eyes shows the impact on the refractive error is about 1.00D when the radius at this surface changes by 1mm.² There is a near 1:1 relationship between a change in corneal back surface astigmatism and change in overall refraction. The algorithm built in each device utilises these data to produce dioptral maps of the surfaces, identifies the orthogonal axes where the averaged dioptral values are highest and lowest in a small series of concentric zones covering the central cornea. The estimation of corneal back surface astigmatism is wholly reliant upon the limitations of the exact method employed to determine the radii over the central region of the corneal back surface.

It is reasonable to assume that there should be close agreement between different instruments designed to measure the same parameter. However, this is not the case regarding the corneal back surface astigmatism. There is a distinct lack of affinity between the corneal back surface astigmatism values obtained by one instrument when compared with another.^{16,42,48–51} For example, Nasser et al⁵⁰ reported the limit of agreement between the Sirius and Pentacam devices for the estimation of corneal back surface astigmatism ranged from −0.56D to +0.31D. Wylęgała et al⁴⁸ compared the performance of Casia, Galilei G6 and Revo NX for the estimation of corneal back surface astigmatism in a series of 94 eyes. The mean values for the corneal back surface astigmatism according to these systems were 0.52D, 0.44D and 0.05D, respectively. Savini et al⁵¹ compared the Sirius and Pentacam devices for the estimation of total corneal astigmatism and found the differences between the two systems amounted to ≥0.50D in over 20% of cases and the axes differed by >10° in over 40% of cases.

The diversity and range of these values lead to the conclusion that results from different instruments are not readily interchangeable. This impacts on our confidence in these estimates and questions the value and clinical relevance of corneal back surface astigmatism. But why are the current advanced technologies yielding such differences? To seek possible answers and gain a better understanding of the relative importance of corneal back surface astigmatism, it is necessary to consider how corneal back surface astigmatism has been estimated in the past, the rationale underpinning some of these procedures and the repeatability and validity of these various techniques.

Estimating Corneal Back Surface Radii, Hence the Astigmatism

During the early stages of 20th century, Tscherning¹ declared the radius of the corneal back surface was 6.22mm while Gullstrand² declared this radius was 6.80mm. A review of the pertinent literature shows that there was a paucity of interest in the radius and shape of the corneal back surface for about six decades. However, there are two publications where the quoted values are quite disparate. In 1973, Lowe and Clarke⁵² reported that the mean radius of this surface along the vertical meridian was typically 6.46mm, and seventeen years later Camellin⁵³ estimated the mean radius was 5.84mm. This difference of +0.62mm changes the overall power of the eye by approximately −0.75D.⁵⁴ This translates to a difference in astigmatism if the difference was orthogonal. Under normal circumstances it is hardly likely for the radius of curvature along one meridian at the corneal back to change by more than 0.50mm. Thus, little attention was paid to investigating the astigmatism and overall shape of the corneal back surface.

Tscherning¹ measured the corneal back surface curvature by injecting the anterior chamber of cadaver eyes with liquid gelatin until it took up the shape of the corneal surface. The cornea was removed, after the gelatin had hardened, to reveal a convex cast of the corneal back surface. The radius of the cast mirrors the curvature of the corneal back surface. Moving on from this totally invasive method, he developed a non-invasive procedure for calculating corneal back surface astigmatism using an ophthalmophakometer (sic). The result obtained using this procedure is dependent upon five variables. Therefore, the validity of the final calculation of corneal back surface astigmatism is totally reliant upon the error in each one of the five variables.

Lowe and Clark⁵² captured slit-lamp images of the corneal profile and matched the shapes of the corneal surfaces with contours of known curvature. The physical limitations of the procedure meant that only an estimate for the corneal back surface radius along the vertical meridian could be made in each case. During that time, the resolution of profile photography for estimating the dimensions of the cornea was heavily criticised for being unreliable.⁵⁵

Royston et al^56,57 modified Tscherning’s non-invasive procedure by capturing the 1st and 2nd Purkinje images of fixed targets positioned along 3 meridians, measuring the corneal front surface radii along the same 3 meridians and the central corneal thickness. The sizes of the Purkinje images together with the other measurements were used to calculate the corneal back surface radii along these meridians using a simple formula. In a series of 15 eyes, the RMS difference between the profile photography and Purkinje image methods for corneal back surface radius was 0.097mm (range 0 to 0.20mm). This is equivalent to a difference in corneal back surface power of about 0.10D.⁵⁷ The test–retest reliability of the Purkinje image technique, based on estimates of corneal back surface astigmatism obtained from 5 eyes, equates to less than 0.03D for power and 3° for the axis. A subsequent paper by the same authors reported mean corneal back surface astigmatism values equivalent to 0.23D (±0.02D, n=40) in females and 0.37D (±0.03D, n=40) in males.³⁷ The corresponding axis values were 88.6° (±4.8) and 91.7° (±4.5). Lam and Douthwaite⁵⁸ used a similar procedure based on Purkinje images and reported that the typical difference between vertical and horizontal corneal back surface radii values was about 0.25mm. This equates to a corneal back surface astigmatism of about 0.30D. To facilitate these procedures, the 1st and 2nd Purkinje images must remain separate and free of any overlap. This limitation means that corneal back surface assessments are made at distances about 3mm, or more, away from the apex of the cornea. Hence, the estimate of corneal back surface astigmatism is for a region of the central cornea no less than 6mm in diameter. It has been shown that the back surface of the cornea flattens gradually from the apex.^54,59 The radius at the apex of the back surface of the cornea is likely to be smaller compared with the figures obtained by these other methods. The actual astigmatism at the apex of the back surface of the cornea could exceed 0.30D in some cases.

Camellin⁵³ devised a geometric method for calculating the radius of the corneal back surface from measurements of front corneal surface radius and topographic corneal thickness. A further development of this technique was used to estimate not only the radius of the corneal back surface but also its' asphericity.^54,59

Fundamental Basis for the Estimation of Corneal Back Surface Radius and Astigmatism

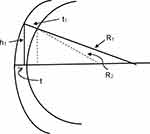
The precise details of the algorithms incorporated into any of the current generation of clinical instruments designed to determine corneal back surface astigmatism are, to some extent, trade secrets. However, Figure 1 shows how corneal back surface radii and astigmatism can be derived. Figure 1 is a diagrammatic representation of a corneal section where the front and back surfaces are centred about a common geometric axis. It can be shown that the radius of the back surface (R₂) can be estimated using the following:

Eq.1

Figure 1 Diagram of a corneal section for the calculation of back surface radius. h1= distance from the apex of the cornea and a peripheral location on corneal surface, t1= thickness of the cornea at this peripheral location on corneal surface, t = thickness at the apex of the cornea, R1 = corneal front surface radius, R2 = corneal back surface radius.

Where, h₁= distance from the apex of the cornea and a peripheral location on corneal surface, t₁= thickness of the cornea at this peripheral location on corneal surface (ie, the length of the perpendicular stretching from this peripheral location on the corneal front surface to the corneal back surface), t = thickness at the apex of the cornea, R₁ = corneal front surface radius, A = h₁ – (h₁·t₁/R₁), B= R₁- √(R₁² – h₁²) and C= t₁² + (h₁·t₁/R₁)^2.

The actual methods built-in the automated instruments for deriving the corneal back surface astigmatism are likely variations of the schema shown in Figure 1. The estimate of corneal back surface radius, hence the astigmatism, is dependent upon four measured variables, t, t₁, h₁ and R₁. The estimates of t₁ and t also depend on the refractive index of the cornea.⁶⁰

The numerical effect of errors in the measurement of, or changes in, the four variables in the estimation of R₂ can be quantified as follows:⁶¹

Eq.2

The partial differential equations demonstrating the theoretical effects on the estimation of R₂ are shown in Table 2.

Table 2 Partial Differential Equations for the Relative Error, , for in the Calculation of Corneal Back Surface Radius

For typical values of R₁ (7.7mm), h₁ (2.0mm), t₁ (0.52mm), and t (0.50mm) reduces Equation 2 to:

Eq.3

When errors in the measurement of δR₁, δh₁, δt₁ and δt = +0.01mm, then δR₂ = −0.02mm. This is an indication of the accuracy in the determination, that is the difference between the true and estimated value, of R_2. The value of δR₂ is negative and indicative of an overestimate of corneal back radius.

In normal eyes, the average change in the astigmatic power of the ocular surface during short intervals of blink suppression is about 0.48D over the central pupillary region of the cornea.⁶² Such a change in ocular surface power would occur when the orthogonal difference in ocular surface radii is about 0.1mm. Therefore, it is reasonable to adopt +0.1mm as a more realistic clinical estimate for δR₁. For δR₁=+0.1mm, keeping δR₁, δh₁, δt₁ and δt = +0.01mm, then δR₂ = +0.04mm. The value of δR₂ is now positive and indicative of an underestimate of corneal back radius. This value for δR₂ is equivalent to an error in corneal back surface power of about −0.04D. As this is the result of a change in ocular surface astigmatism, then 0.04D is a reasonable estimate for the absolute limit of accuracy in the practical determination of corneal back surface astigmatic power.

Nasser et al⁵⁰ found the limits of agreement between the Sirius and Pentacam for the estimation of corneal front surface astigmatism ranged from −0.1mm to 0.12mm. The extent of this range, 0.22mm, equates to a range in the limit of agreement for corneal front surface astigmatism of over 1.25D. This being the range where most of the differences in the estimation of corneal front surface astigmatism lie. Adopting these as values, −0.1mm and 0.12mm, for δR₁ in Equation 3 results in hypothetical values for δR₂ ranging from −0.10mm to +0.06mm when δh₁, δt₁ and δt = +0.01mm. The actual limits of agreement for the corneal back surface astigmatism (in mm) reported by Nasser et al⁵⁰ ranged from −0.54mm to +0.33mm. This range, 0.87mm, is 5.4 times greater than the hypothetical range of δR₂ values of −0.10mm to +0.06mm. In addition, inter-device differences in the estimation of mean corneal thickness can be up to 0.030mm.⁴⁸ Thus, other factors, other values for the uncertainties or differences in h₁, t₁ or t besides +0.01mm could account for the range −0.54mm to +0.33mm. Equation 3 predicts uncertainties in δt₁ and δt are not expected to have much impact on δR₂ when the uncertainties in these parameters are in the same direction, either positive or negative, as such directional uncertainties will cancel each other out. However, by how much does δR₂ vary should δt₁=+0.01mm along one meridian and −0.01mm along another? According to Equation 3, for δR₁ = +0.1mm, δh₁ and δt = +0.01mm, δR₂ = −0.11mm when δt₁=+0.01mm and +0.29mm when δt₁=−0.01mm. This positive-to-negative shift in δt₁ alters δR₂ by +0.40mm. This change in δR₂ increases to +0.59mm when the δt₁ values are adjusted to −0.015mm and +0.015mm. Such uncertainty in δR₂ is equivalent to an uncertainty in corneal back surface astigmatism, and overall refraction, of just under 0.75D. Clearly, there is a profound impact on δR₂ when the regional uncertainties in δt₁ consist of positive and negative values. Inter-device differences for the estimation of corneal back surface astigmatism are amplified when the direction (positive or negative) of uncertainties in the pachymetric estimations is inconsistent. This partially, but not fully, accounts for the reported limits of agreement in the estimation of corneal back surface astigmatism ranging from −0.54mm to +0.33mm.⁵⁰

Turning to δh₁, by how much should this potential source of uncertainty fluctuate to account for these wide limits of agreement? According to Equation 3, when δR₁ = +0.1mm and δt₁ and δt = +0.01mm, the value of δR₂ shifts from −0.54mm to +0.34mm by changing δh₁ from +0.27mm to −0.12mm. The impact of this hypothetical shift in δh₁ on the estimation of corneal back surface astigmatism is just below 1D. Therefore, it is possible for small systematic, meridionally sensitive, differences in the algorithms used by these devices to contribute towards the variations in corneal back surface astigmatism estimates between instruments. Random errors, occurring during the clinical comparison of devices designed to quantify corneal back surface astigmatism, would also contribute to the variance in the data. But such random errors would mask any real differences in the estimation of corneal back surface astigmatism and prevent statistically significant differences from being detected. When the differences between the acquired results are either clinically or statistically significant different, then the reasons are most likely due to systematic differences in the way different devices operate to quantify the same parameter.

Conclusion

The actual astigmatism at the back surface of the cornea cannot yet be measured directly. This astigmatism is an estimate based on several assumptions including the topographic changes in the thickness and front surface radii of the cornea. The hypothetical analysis stemming from Equation 1 is based on several assumptions, such as both corneal surfaces are centred on a common axis, the length of the distances separating the surfaces is perpendicular to the front surface, and it is two dimensional. The analysis does not readily cater for differences in the axes of astigmatism between the corneal surfaces. Furthermore, the dimensions of R₁, t, t₁ and h₁ must be known. None of these factors is measured directly except for h₁. R₁ is an indirect estimate based on the calibration procedures adopted by the manufacturer. Non-contact pachymeters measure the width of the corneal section at various locations and the final computation of t and t₁ rests solely upon the algorithm employed by the manufacturer to interpret the dimensions of the corneal section. The computed t and t₁ values are wavelength dependent and influenced by the refractive index value adopted by the manufacturer. It comes as no surprise that different instruments will provide different estimates of corneal back surface astigmatism when the machines estimate topographic variations in corneal thickness by different rules and algorithms. In addition, the automated systems designed to measure corneal back astigmatism locate the apex of the corneal front surface, while the subject fixates centrally as part of the operational procedure. It is assumed that the location of the 1st Purkinje image is coincident with the apex of the corneal front surface and the visual axis passes through the centre of the pupil. Thus, the true values of both angles kappa and alpha also carry the potential to impact on the estimation of corneal back surface astigmatism. The estimate of corneal back surface astigmatism is an educated guess. It would be a well-educated guess if there was closer, more clinically acceptable, agreement between the results of one instrument and another. It is incumbent on the industry to reach a compromise so that different technologies yield largely similar results. It would be useful if a universally acceptable and realistic model, a procedure, was made available allowing clinics to independently calibrate their system for estimating corneal back surface astigmatism. Such actions would help reduce uncertainty and the discrepancies between instruments designed to measure the same parameter.