Back to Journals » Clinical Pharmacology: Advances and Applications » Volume 8
Population pharmacokinetic modeling of glibenclamide in poorly controlled South African type 2 diabetic subjects
Authors Rambiritch V, Naidoo P , Maharaj B, Pillai G
Received 17 December 2015
Accepted for publication 9 February 2016
Published 12 July 2016 Volume 2016:8 Pages 83—92
DOI https://doi.org/10.2147/CPAA.S102676
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Professor Arthur E. Frankel
Virendra Rambiritch,1 Poobalan Naidoo,2 Breminand Maharaj,1 Goonaseelan Pillai3
1University of KwaZulu-Natal, Durban, 2Department of Internal Medicine, RK Khan Regional Hospital, Chatsworth, South Africa; 3Novartis Pharma AG, Basel, Switzerland
Aim: The aim of this study was to describe the pharmacokinetics (PK) of glibenclamide in poorly controlled South African type 2 diabetic subjects using noncompartmental and model-based methods.
Methods: A total of 24 subjects with type 2 diabetes were administered increasing doses (0 mg/d, 2.5 mg/d, 5 mg/d, 10 mg/d, and 20 mg/d) of glibenclamide daily at 2-week intervals. Plasma glibenclamide, glucose, and insulin determinations were performed. Blood sampling times were 0 minute, 30 minutes, 60 minutes, 90 minutes, and 120 minutes (post breakfast sampling) and 240 minutes, 270 minutes, 300 minutes, 330 minutes, 360 minutes, and 420 minutes (post lunch sampling) on days 14, 28, 42, 56, and 70 for doses of 0 mg, 2.5 mg, 5.0 mg, 10 mg, and 20 mg, respectively. Blood sampling was performed after the steady state was reached. A total of 24 individuals in the data set contributed to a total of 841 observation records. The PK was analyzed using noncompartmental analysis methods, which were implemented in WinNonLin®, and population PK analysis using NONMEM®. Glibenclamide concentration data were log transformed prior to fitting.
Results: A two-compartmental disposition model was selected after evaluating one-, two-, and three-compartmental models to describe the time course of glibenclamide plasma concentration data. The one-compartment model adequately described the data; however, the two-compartment model provided a better fit. The three-compartment model failed to achieve successful convergence. A more complex model, to account for enterohepatic recirculation that was observed in the data, was unsuccessful.
Conclusion: In South African diabetic subjects, glibenclamide demonstrates linear PK and was best described by a two-compartmental model. Except for the absorption rate constant, the other PK parameters reported in this study are comparable to those reported in the scientific literature. The study is limited by the small study sample size and inclusion of poorly controlled type 2 diabetic subjects.
Keywords: type 2 diabetes mellitus, glibenclamide, pharmacokinetics, compartmental, NONMEM model
Introduction
Pharmacometrics is the science that uses mathematics and statistics to characterize, understand, and predict a drug’s pharmacokinetic (PK) and pharmacodynamic behavior.1 Pharmacometrics is minimally present in South Africa.2 Population PK modeling, a component of pharmacometrics, assists with optimization of drug therapy.3 Historically, PK parameters are seldom investigated in South African subjects because of local limited pharmacometric resources. Specifically, the PK of glibenclamide, a second-generation sulfonylurea,4 have not been studied in South African subjects. The Society for Endocrinology, Metabolism, and Diabetes of South Africa currently attempts to phase out the use of glibenclamide because of its tendency to cause severe hypoglycemia, as well as the lack of renal function testing in a significant number of South Africans with diabetes.5 The maximum dose of glibenclamide in South Africa has been reduced since the drug was first introduced onto the market as supported by a dose–response study.6
Despite the limitations of glibenclamide, its ready availability, low cost, and indication for gestational diabetes5 will likely mean that it will be years before it is phased out.
The primary purpose of this analysis was to describe the population PK of glibenclamide in type 2 diabetic South African subjects, so that the estimated PK parameters can be used in the subsequent PK pharmacodynamic (PKPD) modeling to inform appropriate dose selection. In addition, we wanted to compare glibenclamide PK parameters between South African subjects and those reported in the literature.
Data used for population PK modeling
This clinical study was conducted in accordance with the Declaration of Helsinki and its amendments and the Patients’ Rights Charter. The study was approved by the Biomedical Research Ethics Committee of the University of Durban-Westville. All patients provided written informed consent to participate, and the clinical study was previously published.7
Inclusion criteria were as follows: subjects with type 2 diabetes requiring oral antidiabetic therapy; age >20 years; fasting blood glucose >9 mmol/L despite oral antidiabetic therapy; and signed informed consent. Exclusion criteria were being on insulin therapy, allergy to sulfur, and any contraindications to multiple blood sampling, eg, poor venous access. Withdrawal criteria were retraction of consent, intolerance to glibenclamide (eg, allergy to sulfonamides during the study), blood glucose <3.5 mmol/L, and signs or symptoms of hypoglycemia.
A total of 24 subjects with type 2 diabetes were administered increasing doses (0 mg/d, 2.5 mg/d, 5 mg/d, 10 mg/d, and 20 mg/d) of glibenclamide at 2-week intervals. Glibenclamide, glucose, and insulin determinations were performed. There were 24 individuals in the data set who contributed to a total of 841 observation records. Blood sampling times were 0 minute, 30 minutes, 60 minutes, and 90 minutes, 120 minutes (post breakfast sampling) and 240 minutes, 270 minutes, 300 minutes, 330 minutes, 360 minutes, and 420 minutes (post lunch sampling) on days 14, 28, 42, 56, and 70 for doses of 0 mg, 2.5 mg, 5.0 mg, 10 mg, and 20 mg, respectively. Blood sampling was performed after the steady state was reached.
Four subjects (subject numbers: 14, 16, 20, and 24) did not have complete data sets. In the case of subject 14, all ten samples at the dose of 2.5 mg and samples at time 0 hour and 0.5 hours at the dose of 5 mg were lost in transit between the clinical center and the analytical laboratory. Similarly, in subject 20, who completed all doses, ten samples at the dose of 10 mg were lost in transit.
Subject 16 could not proceed with dose escalation beyond 5 mg since blood glucose levels were 3.6 mmol/L after 7 hours. Therefore, there were no concentration versus time profile sets at doses of 10 mg and 20 mg.
Subject 24 absconded from the study after the dose of 2.5 mg. All attempts to contact him were unsuccessful.
Pharmacostatistical model development
Noncompartmental analysis (NCA), implemented in WinNonLin®, provided exploratory data for initial estimates and guides for population PK analysis. This analysis included all those subjects (n=22) who completed the full dose-escalation study and from whom sufficient data were available to characterize concentration versus time profiles.
The structural PK model selected was based on the NONMEM® objective function (OF) value and diagnostic plots.
The structural PK model was implemented in NONMEM by selecting the appropriate ADVAN and TRANS subroutine from the PREDPP library of models. The first-order conditional estimation method with interaction was used throughout this analysis.
Unexplained intersubject variability in structural model parameters was estimated using the following model with the random effect ηj (Equation 1).
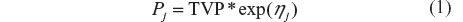
where TVP is the typical value of the PK parameter Pv (eg, CL/f) in the population, Pj is the individual value for P in the jth individual, and ηj is a random variable with mean of zero and variance ωP2. This model assumes a log-normal distribution for the Pj values. Estimates of intersubject variability in P are presented as the square root of ωP2, which is an approximation of the coefficient of variation (CV) of P for a log-normally distributed quantity.
The glibenclamide concentration data were log transformed prior to fitting. The residual error model of this log-transformed data consisted of an additive model as shown in Equation 2.
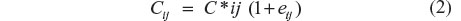
where Cij is the ith concentration measured at time ti in the jth individual. C*ij is the respective model-predicted concentration and the εij is a normally distributed error term with mean of zero and variances. Examples of potential sources of residual variability (depicted as εij in Equation 2) include assay error, deviations from the model specification, and intrasubject variability.
Results
A summary of the baseline characteristics of the study cohort is given in Table 1.
  | Table 1 Cohort characteristics at entry into the study |
NCA showed that there is a linearity between area under the curve (AUC) (AUClast and AUCinf) of glibenclamide with increasing doses. The corresponding values of Cmax also increased linearly. The Tmax ranged from 1.62 hours to 2.09 hours. Clearance (CL/f) ranges from 1.94 L/h to 3.09 L/h, while the half-life ranges from 4.42 hours to 8.08 hours. The volume of distribution (Vz/f) ranges from 14.63 L to 32.48 L. Noncompartmental PK parameters for glibenclamide are presented in Table 2.
A two-compartmental disposition model (Figure 1) was selected after evaluating one-, two-, and three-compartmental models to describe the time course of glibenclamide plasma concentration data. The three-compartment model failed to achieve successful convergence as the intercompartmental transfer rates went to infinity suggesting that the third compartment was poorly identified.
As depicted in the model diagnostic plots (Figures 2 and 3), the one-compartment model gives an adequate description of the data; however, the two-compartment model provided a better fit as judged by a drop in OF value of 188 (−243 versus −431). All attempts to model observed enterohepatic recirculation were unsuccessful. Visual inspection of Figure 4 indicates that subjects 4, 7, 9, 10, and 14 all showed potential enterohepatic recycling (EHC) of drug at 20 mg and subjects 4, 9, and 10 at 10 mg of glibenclamide. The EHC of glibenclamide was not therefore captured in a pharmacokinetic model since the majority of subjects (19) did not show EHC, and also because there were not enough data points to fully characterize the EHC profile.
  | Figure 2 Model diagnostics: observed versus model predicted concentrations for the one-compartment model shown as points in the graph. |
  | Figure 3 Model diagnostics: observed versus model predicted concentrations from the final two-compartment model shown as points in the graph. |
The final model was subjected to a posterior predictive check (PPC).8 In this procedure, 500 replications were run using the fixed and random effects from the final population PK model and using a study design identical to that used in this study. The median AUC for each dose from each replicate was calculated, and the distribution of AUC values was compared with the median for each dose level calculated using NCA methods. Figure 5 shows that the observed (NCA) median AUC falls within the distribution of simulated AUC values confirming the good predictive ability of the model.
The PK parameters of glibenclamide from the one-compartment and the final two-compartment models are presented in Table 3. Individual PK parameters, obtained from the two-compartment model, are presented in Table 4. The PK of glibenclamide is linear after multiple-dose administration in the dose range of 2.5–20 mg as suggested by the model diagnostic boxplots of population PK parameters versus dose (Figure 6).
Discussion
PK parameters derived from NCA
This discussion provides a comparison of results obtained from NCA in this study to that reported in the literature. The NCA analysis also provided initial estimates and guided the population PK analysis.
The “clearance” of glibenclamide in this study population ranges from 1.94 L/h to 3.09 L/h. The mean age of this population is 54.1 years, ranging from 39 years to 73 years. The mean creatinine of the study population is 64.1 μmol/L, which is within the normal range, and therefore it is assumed to have normal renal function. The clearance of glibenclamide in this study population is within the range reported by other researchers who investigated type 2 diabetics with normal renal function and of the same age group: Jaber et al,9 3.2 L/h; Jönsson et al,10 4.41 L/h (Caucasians) and 4.1 L/h (Chinese); and Jönsson et al,11 3.7 L/h.
The apparent volume of distribution (Vz/f) of this study population ranged from 14.63 L to 32.48 L and is consistent with the literature. Jaber et al9 reported values of 20 L, 41 L, and 51 L, after 0 week, 6 weeks, and 12 weeks, respectively, of glibenclamide therapy. Jönsson et al10 in his comparison of Caucasian and Chinese subjects reported values of 6.31 L and 5.49 L, respectively.
The “half-life” (t1/2) of glibenclamide in this study ranged from 4.42 hours to 8.08 hours. Marble et al12 and White and Keith Cambell13 reported half-lives of 6–10 hours. This half-life is within the range as reported for type 2 diabetic patients (the half-life for micronized glibenclamide ranged from 2.1 hours14 to 8.3 hours).15 Jaber et al8 reported a half-life of 12.2 hours, Jönsson et al16 7.09 hours, and Jönsson et al10 2.0–4.5 hours for Caucasian and Chinese. Courtois et al17 reported half-lives of 2.63 hours (42–59 years) and 2.78 hours (71–75 years).
There is a linear increase in the maximum glibenclamide blood concentration (Cmax) as the dose of glibenclamide is increased from 2.5 mg to 20 mg, that is, 157.97 ng/mL to 773.61 ng/mL, respectively.
Cmax reported in this study is approximately twice that reported for corresponding doses by other researchers, namely, for the dose of 5 mg, Fleishaker and Phillips15 reported a Cmax of 179 ng/mL and Coppack et al14 reported a Cmax of 241 ng/mL and 354 ng/mL for 10 mg (fasting) and 20 mg (fasting) of glibenclamide, respectively, while Jaber et al8 reported a Cmax of 278 ng/mL for 2.5 mg (in solution) of glibenclamide in solution and Jönsson et al10 reported a low max of 69 ng/mL (Caucasians) and 82 ng/mL (Chinese) for 2.5 mg of glibenclamide. However, when 1.25 mg of glibenclamide was given intravenously, the Cmax was appreciably higher (376 ng/mL [Caucasian] and 368 ng/mL [Chinese]].10 This wide variation in Cmax is indicative of the variable bioavailability of glibenclamide. This is confirmed by the very high Cmax obtained by Jönsson et al.11
The time taken to reach Cmax (Tmax) of 1.62–2.09 hours is comparable to the values reported in the literature.8,10,11,14,16,17 However, as shown in this study, there is no coincidence in the Tmax of glibenclamide, glucose, and insulin.
Population PK model selection
Three population PK models were fitted to the glibenclamide PK data using nonlinear mixed effects modeling. While both the one- and two-compartment models terminated successfully, and produced similar graphical model diagnostic plots, the two-compartment model provided a better comparative fit due to its significantly lower OF (−243.409 versus −431.164). A three-compartment model was also attempted but was considered over parameterized as the model failed to achieve successful convergence due to the intercompartment transfer rate constants being estimated as infinite. This suggested that the third compartment was poorly defined.
Despite extensive attempts at model refinement, the EHC model did not converge successfully. This is possibly due to a wide between-subject variability as well as within-subject variability in EHC, ie, some subjects show evidence of EHC at some doses but not at other dose levels. Furthermore, there were not enough data points to fully characterize the EHC profile in all subjects. This model was eventually abandoned, and the two-compartment model was accepted as the final model. It was acknowledged that the poorly fitted EHC component of the profile in the final model would contribute to an inflated residual variability due to model misspecification. Despite this drawback, however, the two-compartment model provided a good fit of the model to the data as confirmed by the PPC. In particular, the model was able to provide an estimate of exposure (AUC) to glibenclamide that was consistent with the NCA estimates. This was important since one use of the PK model was to provide an estimate of average glibenclamide concentration (Cpss) for use as the driving force in a PKPD model. PPC is a method for the objective assessment of the predictive ability of a model and is a robust method for model evaluation. Yano et al8 concluded that “if a PPC invalidates a model, one can be reasonably certain that the model has serious deficiencies.”
The low relative standard error (SE) indicated the good precision of the estimated parameters and the anticipated relatively high residual variability was also noted (43.5% CV). The residual variability consists of assay error, deviations from the model specification, and intrasubject variability. In the final two-compartment model selected, one source of model misspecification is the inability to characterize the EHC of glibenclamide that was noted in several subjects. In addition, in some subjects, the predose glibenclamide concentration was also not well fitted by the model. This might reflect the lower degree of confidence in the dosing history (compliance with regard to timing and size of dose or even administration) for the unsupervised doses that contribute to the predose concentration.
Individual plots of the glibenclamide concentration versus time profiles from the final two-compartment model show a very close agreement between the observed and model predictions. The relatively low between-subject variability in clearance (~34% CV) and apparent volume of distribution (~23% CV) suggested that covariates might not significantly improve the population fit. In addition, graphical examination of the PK parameters versus covariates did not reveal any obvious relationships. Consequently, no formal covariate analysis was conducted.
Population PK parameters
The PK parameters derived from the two-compartment model are discussed in relation to published data.
Glibenclamide is completely absorbed after oral administration, and the rate and extent of absorption are not affected by food.8 Therefore, estimates for clearance and volume of distribution after oral administration are considered to be close approximations of those after intravenous administration. In this study, the dose of glibenclamide was taken on an empty stomach, 10 minutes before breakfast.
Using a one-compartment model, the Vd was 38.90 L (0.55 L/kg), which approximates that reported by Tracewell et al18 (43.7 L; 0.509 L/kg) in their study of glibenclamide PK using a one-compartment model with first-order absorption and first-order elimination. Other studies quoted by Tracewell et al18 report Vd values of 0.735±0.0150 L/kg, 0.19±0.01 L/kg, 0.125±0.008 L/kg, 0.017±0.00714 L/kg, 0.200±0.032 L/kg, 0.144±0.0156 L/kg, 0.0413±0.000975 L/kg, and 0.57±0.57 L/kg. Jaber et al8 reported a Vd of 51±51 L/h using a one-compartment model after a 12-week study. The Vd of this population is within the range reported in the literature.
The volume of distribution ± SE of glibenclamide for the two-compartment model is 11.70±1.11 L and 68.1±6.0 L for the central and peripheral compartments, respectively. This difference may be due to the separation of the compartments during modeling.
The average clearance for glibenclamide is 1.52±0.12 L/h (0.02 L/h/kg) for the one-compartment model and 2.16±0.16 for the two-compartment model. The intercompartmental clearance (Q/f) is 3.84±0.58 L/h. Tracewell et al18 reported average values for glibenclamide clearance of 0.0387±0.00642 L/h/kg in younger diabetics (<60 years) and 0.0525±0.00349 L/h/kg in older subjects (>60 years). Other studies quoted by Tracewell et al18 reported clearance values of 0.107±0.051 L/h/kg, 0.078±0.00516 L/h/kg, 0.0634±0.00803 L/h/kg, 0.09±0.03 L/h/kg, 0.078±0.029 L/h/kg, and 0.0394±0.00891 L/h/kg. In addition, Jaber et al,9 Jönsson et al,16 and Jönsson et al,11 reported clearance values ±SE of 3.2±2.1, 4.41 L/h (range 3.38–8.11 for Caucasians) and 4.10 L/h (range 2.91–5.98 for Chinese); and 3.70 L/h (1.15), respectively. The clearance value obtained for this study (mean age: 54.1±9.2 years) falls within the range of other reported studies and that of Tracewell et al18 for their study population aged <60 years.
The average Ka (±SE) is 2.39±0.34 h−1 (one-compartment model) and 0.53±0.04 h−1 (two-compartment model). Jönsson et al,11 Ryderberg et al,19 and Tracewell et al18 reported Ka values of 2.68±1.50 h−1, 0.756 h−1, and 0.057±0.244 h−1, respectively. Reppas20 reported that the variation in Ka values may be due to kinetic sensitivity, linearity, specificity, and precision.
Furthermore, the sampling interval in the absorptive phase coupled with variations in physiological factors may also contribute to this wide variation.
Limitations of this study include the small study sample and inclusion of poorly controlled type 2 diabetic patients. Extrapolation of the study findings to the greater population must be performed with caution. Nevertheless, the study does serve as a starting point to understand the PK of glibenclamide in type 2 diabetic subjects, which has not been previously reported.
Conclusion
PK results obtained from NCA did not differ in any marked way from those obtained from the mixed effects modeling (NONMEM) results. The PK parameters of glibenclamide obtained from the NCA are consistent with those obtained from the literature. The PK of glibenclamide in this study population was described by a two-compartmental disposition model with first-order absorption. The PK of glibenclamide in this study population is comparable to that reported in the literature, save for the absorption rate constant. The model was subjected to internal validation using the PPC approach and provided acceptable model predictions. The study is limited by the small sample size and inclusion of poorly controlled type 2 diabetic patients.
Disclosure
G Pillai has stocks in Novartis. The other authors report no conflicts of interest in this work.
References
Ette EI, Williams PJ. Pharmacometrics:The Science of Quantitative Pharmacology. Hoboken. NJ: John Wiley and Sons, Inc; 2007. | |
Pillai G, Davies G, Denti P, et al. Pharmacometrics: opportunity for reducing disease burden in the developing world: the case of Africa. CPT Pharmacometrics Syst Pharmacol. 2013;28(2):e69. | |
Ahmad AM. Recent advances in pharmacokinetic modeling. Biopharm Drug Dispos. 2007;28(3):135–143. | |
Feldman JM. Glyburide: a second-generation sulfonylurea hypoglycemic agent. History, chemistry, metabolism, pharmacokinetics, clinical use and adverse effects. Pharmacotherapy. 1985;5(2):43–62. | |
Amod A, Ascott-Evans BH, Berg GI, et al; Guideline Committee. The 2012 SEMDSA guideline for the management of type 2 diabetes (revised). JEMDSA. 2012;17(2):S1–S95. (Supplement 1). | |
Rambiritch V, Naidoo P, Butkow N. Dose-response relationships of sulfonylureas: will doubling the dose double the response? South Med J. 2007;100(11):1132–1136. | |
Rambiritch V, Maharaj B, Naidoo P. Glibenclamide in patients with poorly controlled type 2 diabetes: a 12-week, prospective, single-center, open-label, dose-escalation study. Clin Pharmacol. 2014;4(6):63–69. | |
Yano Y, Beal SL, Sheiner LB. Evaluating pharmacokinetic/pharmacodynamic models using the posterior predictive check. J Pharmacokinet Pharmacodyn. 2001;28(2):171–192. | |
Jaber LA, Antal EJ, Slaughter RL, Welshman IR. Comparison of pharmacokinetics and pharmacodynamics of short and long-term glyburide therapy in NIDDM. Diabetes Care. 1994;17(11):1300–1306. | |
Jönsson A, Chan JC, Rydberg T, et al. Pharmacodynamics and pharmacokinetics of intravenous glibenclamide in Caucasian and Chinese patients with type-2 diabetes. Eur J Clin Pharmacol. 2000;55(10):721–727. | |
Jönsson A, Rydberg T, Sterner G, Melander A. Pharmacokinetics of glibenclamide and its metabolites in diabetic patients with impaired renal function. Eur J Clin Phamacol. 1998;53(6):429–435. | |
Marble A, Weir GC, Selenkow HA, et al. Endocrine diseases. In: Speight TM, editor. Avery’s Drug Treatment:Principles and Practice of Clinical Pharmacology and Therapeutics. 3rd ed. Auckland: Adis; 1987:522–590. | |
White JR Jr, Keith Cambell R. Diabetes mellitus. In: Herfindal ET, Gourley DR, editors. Textbook of Therapeutics, Drug and Disease Management. 6th ed. Philadelphia, USA: Williams and Wilkins; 1996:357–386. | |
Coppack SW, Lant AF, McIntosh CS, Rodgers AV. Pharmacokinetic and pharmacodynamic studies of glibenclamide in non-insulin dependent diabetes mellitus. Br J Clin Pharmacol. 1990;29(6):637–684. | |
Fleishaker JC, Phillips JP. Evaluation of a potential interaction between erythromycin and glyburide in diabetic volunteers. J Clin Pharmacol. 1991;31(3):259–262. | |
Jönsson A, Chan JC, Rydberg T, et al. Effects and pharmacokinetics of oral glibenclamide and glipizide in Caucasian and Chinese patients with type-2 diabetes. Eur J Clin Pharmacol. 2000;56(9–10):711–714. | |
Courtois P, Sener A, Herbaut C, Turc A, Malaisse WJ. Pharmacokinetics of gliquidone, glibenclamide, gliclazide and glipizide in middle-aged and aged subjects. Res Commun Mol Pathol Pharmacol. 1999;103(2):211–222. | |
Tracewell WG, Stalker DJ, Maloley PA, Gallagher TE, Gwilt PR. Population pharmacokinetics of glyburide in patients with well controlled diabetes. Pharmacotherapy. 1998;18(1):51–56. | |
Rydberg T, Jönsson A, Karlsson MO, Melander A. Concentration-effect relations of glibenclamide and its active metabolites in man: modelling of pharmacokinetics and pharmacodynamics. Br J Clin Pharmacol. 1997;43(4):373–381. | |
Reppas C [webpage on the Internet]. The Assessment of the Absorption Rate in Bioequivalence Studies: What Do We Really Want to Know? Third European Intensive Course on New Forms and New Routes of Administration for Drugs. 1997. Available from: http://old.unipr.it/arpa/dipfarm/news/newstill2000/erasmus/erasm3.html. Accessed June 22, 2015. |
 © 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.







