Back to Journals » International Journal of Nanomedicine » Volume 11
Monte Carlo simulations guided by imaging to predict the in vitro ranking of radiosensitizing nanoparticles
Authors Retif P, Reinhard A, Paquot H, Jouan-Hureaux V , Chateau A, Sancey L, Barberi-Heyob M, Pinel S , Bastogne T
Received 25 April 2016
Accepted for publication 29 June 2016
Published 18 November 2016 Volume 2016:11 Pages 6169—6179
DOI https://doi.org/10.2147/IJN.S111320
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Thomas Webster
Paul Retif,1–3 Aurélie Reinhard,2,3 Héna Paquot,2,3 Valérie Jouan-Hureaux,2,3 Alicia Chateau,2,3 Lucie Sancey,4 Muriel Barberi-Heyob,2,3 Sophie Pinel,2,3 Thierry Bastogne2,3,5
1Unité de Physique Médicale, CHR Metz-Thionville, Ars-Laquenexy, 2Université de Lorraine, 3CRAN, UMR 7039, CNRS, Vandoeuvre-lès-Nancy, 4Institut Lumière Matière, UMR 5306, CNRS, Villeurbanne, 5INRIA-BIGS & CRAN, Université de Lorraine, Vandoeuvre-lès-Nancy Cedex, France
Abstract: This article addresses the in silico–in vitro prediction issue of organometallic nanoparticles (NPs)-based radiosensitization enhancement. The goal was to carry out computational experiments to quickly identify efficient nanostructures and then to preferentially select the most promising ones for the subsequent in vivo studies. To this aim, this interdisciplinary article introduces a new theoretical Monte Carlo computational ranking method and tests it using 3 different organometallic NPs in terms of size and composition. While the ranking predicted in a classical theoretical scenario did not fit the reference results at all, in contrast, we showed for the first time how our accelerated in silico virtual screening method, based on basic in vitro experimental data (which takes into account the NPs cell biodistribution), was able to predict a relevant ranking in accordance with in vitro clonogenic efficiency. This corroborates the pertinence of such a prior ranking method that could speed up the preclinical development of NPs in radiation therapy.
Keywords: biomedical applications of radiations, computer simulation, nanomedicine, virtual screening
Introduction
Radiosensitizing nanoobjects are becoming a major innovation in the field of radiation therapy with the promise of a breakthrough in anticancer therapies.1,2
Since the early 1990s, the number of articles published on the subject has kept increasing.3 Unfortunately, as it has been mentioned in 2013 by Etheridge et al,4 “Many of the revolutionary nanomedicine technologies anticipated in the literature may be 20 or more years from clinical use”. Indeed, only a few nanoparticle (NP)-radiation therapy combinations are undergoing clinical trials (only 3 records concerning NBTXR3 devices in ClinicalTrials.gov).5
In order to speed up the preclinical development of radiation therapy enhancing NPs, numerous studies have tried to predict their in vitro or in vivo radiosensitizing effect.6–9 The most common method, inherited from the practices of physics, is to use Monte Carlo simulators of particle transport in matter such as BEAM, MCNP, PENELOPE or Geant4.10–13 First attempts did not show satisfactory results. According to Butterworth et al,14 biological effects cannot, indeed, be accurately predicted on the basis of the gold NP concentration and beam energy, and they suggest oxidative stress as a central mechanism in mediating response. Yet, it should be nuanced as results are likely to depend on the simulation parameters. That is why in a recent comment, McMahon et al15 have highlighted the fact that theoretical prediction scenarios and values should be meaningful within a therapeutic context.
Conversely to previous published studies, the goal herein is not to predict the X-rays dose enhancement effect of the studied NPs. Instead, as a step forward toward an efficient prediction of their radiosensitizing effects, we have preferred to develop a simple yet effective in silico method to predict an in vitro ranking of radiation-enhancing NPs. In fact, the suggested computerized method in this article could make it possible to select, from a high number of nanoobjects, the one providing the most promising results, thus speeding up the preclinical development of radiosensitizing NPs.
For this aim, in this article we compare 2 Monte Carlo approaches: 1) a classical one, not taking the cellular biodistribution of NP into account, we call it scenario A and 2) our virtual screening that is called scenario B. Each method is used to establish an in silico ranking of 3 radiosensitizing NPs in U87 glioblastoma cells. Results of both scenarios were then compared with in vitro experiments (reference), which had been carried out prior to the Monte Carlo simulations.
While the ranking predicted in the scenario A did not fit the reference at all, in contrast, we showed for the first time how our in silico virtual screening method (scenario B), based on few in vitro experimental data, was able to provide us results in accordance with in vitro responses, therefore illustrating the relevant remarks of McMahon et al15 related to theoretical prediction scenarios.
Overview of the ranking process
Before illustrating our concept using the aforementioned scenarios A, B and reference results, we would like to give the reader an overview of our virtual screening process used in the scenario B.
Comparing or optimizing NP designs usually requires several experiments that are not only expensive but also time-consuming.4 The fundamental objective of our work was to elaborate a virtual screening process designed to quickly draw a relevant ranking of a high number of radiosensitizing NPs with as few experiments as possible. The number of experiments would then be drastically reduced compared with a standard approach. Once the computerized ranking has been established, the user could select a sample of the best NPs on which the user could perform the proper biological assays necessary to validate or refine the selection.
Before describing our ranking methodology, the reader should be aware that it was based on several assumptions.
A1. | First, the radiosensitizing power of NPs is likely to be not entirely linked to the DNA damages.16–19 Thus, the integrated or average dose deposited in the cell is an interesting information that could be correlated with the overall performance of a NP. |
A2. | Then, it is mandatory to account for the intracellular distribution of NPs in the Monte Carlo simulator.20,21 For instance, a transmission electron microscopy (TEM) image can be used to assess the intracellular colocalization and the topology of each NP in each cell line. An inductively coupled plasma optical emission spectrometry (ICP-OES) quantification could be used as well to refine the results.22 Each scenario should be modeled afterward and should reflect information shown by TEM images and the ICP quantification. This assumption was illustrated by the comparison of the 2 scenarios A and B. |
A3. | Finally, the radiosensitizing power of NPs was accurately assessed in vitro by clonogenic assays whose results can be plotted as survival curves representing the fraction of surviving cells as a function of the dose.23 |
The suggested methodology was composed of 4 logical steps that should be carried out in order.
S1. | First, the different combinations of NP/cell and radiation types should be well established. If necessary, a design of numerical experiments strategy could be used in order to speed up the simulation process. |
S2. | For each combination that will be modeled in the simulator, the number of NPs in 1 cell as well as the size and distribution of NP clusters should be experimentally assessed. |
S3. | The biodistribution of each combination in 1 cell should be faithfully modeled. The irradiation source chosen in the simulator should be close to the real one. |
S4. | After the simulation is done, the mean dose in the cell should be recorded for each combination then NPs should be ranked with respect to it. |
As aforementioned, in order to strengthen our approach, we carried out a preliminary experimental validation using 3 types of NPs on U87 glioblastoma cells monolayer cultures irradiated using a 6 MV photon beam from a clinical accelerator.
Experiments
NP and cell characteristics
NPs
Iron (20 nm Fe3O4 with a polyvinylpyrrolidone (PVP) surface modified for biomedical applications, NanoXact formulation) and gold (20 nm with a PVP surface and 50 nm with a polyethylene glycol [PEG] surface, BioPure formulation) NPs, suspended in water, were purchased from nanoComposixTM Inc. (San Diego, CA, USA) at a concentration of 20 or 1 mg/mL, respectively. The stock suspensions were diluted appropriately to the required concentration in culture medium immediately prior to use.
NP sizes were determined using Nanoparticles Tracking Analysis NTA 2.3 software on NanoSight system (Malvern Instruments Ltd, UK) and TEM.
Cells
Human primary glioblastoma cell lines U87 MG (ATCC® HTB-14TM; LGC Standard, France) were cultured in Dulbecco’s Modified Eagle’s Medium (DMEM) complemented with 10% fetal bovine serum, 0.4% L-asparagine, 0.36% L-serine, 1% L-glutamine, 1% essential amino acids, 0.5% nonessential amino acids, 0.4% vitamins, 1.25% sodium pyruvate and 1% penicillin streptomycin. Cells were maintained in monolayers in a tissue culture incubator at 37°C with 5% CO2 95% air. DMEM and amino acids were purchased from Gibco (Life Technologies, France) while other reagents were obtained from Sigma-Aldrich.
Distribution and quantification of NPs in cells
TEM imaging
First, 0.8×104 cells were plated in 96-well plates for 3 days and then exposed to 50 μg/mL of NPs for 24 h. After 2 washes with Hank’s balanced salt solution (HBSS; Sigma-Aldrich, France), cells were primary fixed with glutaraldehyde 2.5% in sodium cacodylate buffer 0.1 M pH 7.2 followed by a post-fixation step using osmium tetroxide 1% in sodium cacodylate buffer after several washings. Then, cells were rinsed again and dehydrated through a graded series of ethanol concentrations (30, 50, 70, 80, 90, and 100% for 5 min each) and embedded in epoxy-based resin (Embed 812, DDSA, NMA, and DMP30; Electron Microscopy Sciences, France). After resin polymerization and plastic dissolution with xylene, samples were cut in 90 nm thick slices using Ultra-cut E ultramicrotome (Reichert-Yung). Finally, the ultrathin sections were deposited onto carbon–Formvar copper grids and observed under a CM12 electron microscope (Philips, France) operated at 80 kV. Photographs were taken using ITem software (Olympus, France).
ICP-OES quantification
For the intracellular NP quantification, 1.5×106 cells were plated in 175 cm2 culture dishes for 3 days, and then exposed to different samples of NPs for 1 or 24 h. After incubation time, 1 mL of culture supernatant was collected; cells were washed 3 times with phosphate-buffered saline, trypsinized, counted and centrifuged for 10 min at 300 g to obtain dry pellet.
Au or Fe content in supernatant and cell samples was determined using ICP-OES. The samples were dispersed in 5 mL of aqua regia (67% HNO3/37% hydrochloric acid (w/w)) for 4 h at 80°C. Subsequently, the samples were diluted with a HNO3 5% (w/w) matrix to adjust the volume to 10 mL; the samples were then filtered (0.22 μm) and analyzed by ICP-OES to determine the elemental content with a precision of 5%. For calibration of the ICP-OES, single-element standard solutions were prepared by successive dilution in a HNO3 5% (w/w) matrix from a 1,000 ppm Au or Fe standard acquired from SCP Science (Quebec, Canada).24
Irradiation setup
A total of 2.5×105 cells were plated in 25 cm2 culture dishes containing culture medium for 48 h. The medium was removed, and cells were exposed to fresh medium containing NPs for 24 h. Cells were irradiated using a 6 MV photon beam from a Clinac® iX (Varian Medical Systems, Palo Alto, CA, USA) medical accelerator with respect to the scheme presented in Figure 1. The skin–source distance was set to 100 cm, well plates were placed between 3 and 6 cm PTW RW3 water-equivalent slabs in order to take the build-up and the backscatter (respectively) into account. The field size was set to 30×30 cm so that a maximum of 4-well plates could be irradiated simultaneously. Monitor units were calculated so that a dose of 2, 4, 6 or 10 Gy (±5%) was deposited into the well plates. Twelve hours after the irradiation, cells were washed with phosphate-buffered saline, trypsinized, diluted 4-fold to allow sufficient plating volume, homogenized by aspiration/reflux with a 21 G needle mounted on a syringe to achieve a single cell suspension, counted and replated for survival analysis.
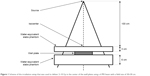  | Figure 1 Scheme of the irradiation setup that was used to deliver 2–10 Gy in the center of the well plates using a 6 MV beam with a field size of 30×30 cm. |
In vitro reference results
The cell survival was assessed using clonogenic assays. A total of 104 cells were plated in 6-well plates and incubated for 12 days at 37°C 5% CO2 95% air. Surviving colonies were stained with 1 mL of 3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide solution (1 mg/mL; Acros Organics; Thermo Fisher Scientific, France) and counted using GelCount™ (Oxford Optronix, Abingdon, UK). Results of the clonogenic assays were plotted as survival curves showing the fraction of surviving cells as a function of the dose deposited in the well plates.
Numerical modeling and simulation
General information on our simulations
Monte Carlo simulator
For the present study, we used GATE 7.0 with the Geant4 9.6.p03 and CLHEP 2.1.3.1 libraries. The pseudorandom number generator was the Mersenne Twister. We chose the Livermore physics list and activated Rayleigh scattering, photoelectric, Compton scattering, pair conversion, electron ionization and Bremsstrahlung effects. For the multiple scattering, we chose the Urban95 model. More information about the parameters of our physics list can be found in Table 1. Auger electrons emission was activated through the atomic deexcitation functions. The energy and spatial cutoffs were set to 250 eV and 10 nm, respectively.
  | Table 1 Physics list parameters and values |
Geometry of the simulation
The geometry entered in the simulator was highly simple (Figure 2): a water cube (edge size of 1 mm) containing a spherical structure standing for a U87 cell (radius of 6 μm). Then depending on the NP being evaluated, a random distribution taking both the size and the number of clusters into account was generated inside the spherical cell structure. A cluster of NPs is defined as a group of NPs that are spatially close together in a cell. In the simulator, each cluster is a spherical structure containing a fixed number of NPs that are randomly distributed in it. Each NP is also modeled as a spherical structure. Each volume material was set to G4_WATER except the NPs that were either gold or iron structures.
Source specification
A cylindrical source (radius of 6 μm, height of 1 nm) was placed 1 cm away from the cell structure. The primary photon beam spectrum (Figure 3) was based on a 6 MV, 10×10 cm beam calculated by Ding25 in 2002 for which the contributions ≥1 MeV were not used in order to significantly accelerate the calculation time.
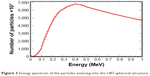  | Figure 3 Energy spectrum of the particles entering into the U87 spherical structure. |
Runs and results
Each scenario was cut into 21 runs launched on a parallel calculation platform. Each run had a different engine seed. For each run, a total number of 1010 primaries were tracked.
At the end of the simulations, the following results were recorded: 3D dose images (cube with an edge size of 12 μm), secondary species production in the cell structure and a spectrum of the energy deposited in the cell structure. The analysis of the results was done using ROOT 5.34/32, ImageJ 1.49d, R and locally developed macros.26–28 Mean doses in the cell were assessed using the following 2 methods: a measurement on the 3D dose images and the integration of the energy deposited in the cell spectra.
Scenario A: classical Monte Carlo simulations
In order to prove that Monte Carlo simulations should preferentially take the biodistribution of the NPs into account, we have chosen to establish a ranking of our 3 NPs on the basis of classical Monte Carlo simulations. By “classical Monte Carlo simulation” we mean that they are not based on a preliminary evaluation of intracellular distribution of NPs. These simulations have been extensively detailed in the literature.8,29,30 In this counterexample, we have decided to fix the number of clusters (=10), the number of NPs per cluster (=100) and radius of each cluster (=250 nm), which are the same for our 3 NPs.
Scenario B: our virtual screening process
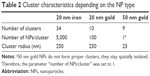
Concerning our virtual screening process, number of clusters, clusters sizes and number of NPs per cluster were determined experimentally via ICP-OES and TEM imaging. Values of these parameters are summarized in Table 2.
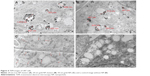
Examples of TEM images of U87 cells with and without NPs are shown in Figure 4. Numerous measurements of the cluster sizes for each type of NP lead us to the choice of the parameters summarized in Table 2.
Results
In vitro analysis
Assessment of radiosensitizing effects of the NPs by clonogenic assays
As this technique is considered as the gold standard in radiation biology, the radiosensitizing potential of the 3 previously described NPs was determined by clonogenic assays. U87 glioblastoma cells were exposed to gold or iron NPs at 50 μg/mL for 24 h prior to irradiation with 6 MV X-rays. Figure 5 shows the radiation dose–response curves for U87 cells exposed or not to NPs. Surviving fractions were normalized to that of nonirradiated control cells in each of the experiments to correct for the direct cytotoxic effect of organometallic NPs. Dose–response curves of the form SF = exp[-(αD + βD2)] (with SF being the survival fraction, D the dose of radiations in Gy and α, β radiobiological curve fitting factors) were fitted to the data using least squares minimization, weighted using the standard error of each measurement. Statistical errors on fit values were calculated with 95% CI. The radiobiological parameters for each NP are summarized in Table 3. Results showed improvement in the response of U87 cells to radiation in the presence of 20 nm NPs, as compared to control cells without NPs. The most significant response was obtained with 20 nm iron NPs compared to radiation only controls (eg, at 2 Gy, P=0.005). Therefore, there are strong presumptions to reject the null hypothesis, which means that the mean values were statistically different. Dose enhancement factors were calculated as the ratio of doses required to give the same surviving fractions as that of the radiation only control cells at a dose of 2 Gy (SF2). Dose-modifying factors were approximately 1.064, 0.948 and 0.783 for 50 nm gold, 20 nm gold and 20 nm iron NPs, respectively.18
  | Table 3 Radiobiological curve-fitting parameters for each NP |
TEM observations of NP cellular uptake
After NPs incubation with cells, samples were prepared for TEM analysis. Whatever the NPs studied, they are trapped in macropinocytosis and endocytosis vesicles with a size of 250–1,250 nm, and clearly delineated by a membrane. While 50 nm gold NPs were found as single objects in vesicles (1–2 NPs per vesicle), we have mainly observed agglomerates for 20 nm gold and 20 nm iron NPs. The TEM images show a higher number of clusters for 20 nm iron than for 20 nm gold NPs. ICP-OES analyses confirmed that NPs uptake in U87 cells was more important for 20 nm iron than for 20 or 50 nm gold NPs.
Monte Carlo ranking results
For each simulation, the mean dose was measured on the 3D dose images using ImageJ. Values were normalized so that the mean dose in water over the 21 runs is equal to 100.00%. We also measured the mean dose deposited into the cell on the spectrum of the energy using ROOT and found that both measurements gave the same results (example of an energy deposition histogram of a 20 nm iron NP, run #1, Figure 6).
  | Figure 6 Spectrum of the energy deposited into the cell structure with 20 nm iron NP clusters. |
Scenario A
Concerning the scenario A, the mean values of the 21 runs ± 95% CI are shown in Figure 7 and Table 4. The following ranking has been established using this classical simulation process (from worse to best): 20 nm iron NP, 20 nm gold NP, and 50 nm gold NP. Since its 95% CIs were not overlapping with others, only the dose enhancement result of the 50 nm gold NP was statistically different from the remaining ones.
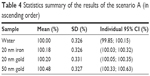  | Table 4 Statistics summary of the results of the scenario A (in ascending order) |
Scenario B
Regarding the scenario B, results for each run and each type of NP are shown in Figure 8; the mean values of the 21 runs ± 95% CI are shown in Figure 9 and Table 5. The following ranking has been established using our virtual screening process (from worse to best): 50 nm gold NP, 20 nm gold NP, and 20 nm iron NP. Since their 95% CIs are not overlapping with others, only the dose enhancement result of the 20 nm iron NP is statistically different from the remaining ones.
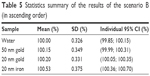  | Table 5 Statistics summary of the results of the scenario B (in ascending order) |
Discussion and conclusion
First, the dose enhancement results shown in Tables 4 and 5 seemed surprisingly low compared to some values published in the literature.30,31 It is likely a consequence of the fact that the dose was averaged over the whole cell structure whose volume is much larger than that of the clusters (eg, the cell structure’s volume is 904.8 μm3 while the sum of the iron NP clusters’ volume is 2.2 μm3). A visual analysis of the 3D dose images highlights that the deposited dose is locally enhanced in the vicinity of NP clusters. An example of a 3D dose image (from the scenario B) in the presence of iron NPs is shown in Figure 10.
Then, as it can be seen when comparing Figures 7 and 9 as well as Tables 4 and 5, the scenario A ranking was completely different than that of scenario B. Indeed, in the classical Monte Carlo ranking, the NP showing the highest radiosensitizing potential was the 50 nm gold NP whereas the worse NP seemed to be the 20 nm iron NP. However, referring to the reference in vitro results shown in Table 3, there was no doubt that the correct ranking was established in the scenario B, which corresponds to our virtual screening process. We thus believe that both the distribution and the quantity of NPs in the cell should be experimentally evaluated before taking them into account to run Monte Carlo ranking computations, which is the originality of our approach.
Figure 11 compares 2 alternative approaches to rank the radiosensitizing effects of NPs: an in vitro and classical method versus our in silico and innovative technique. As it is shown in this figure, our accelerated in silico process could save up to 56 days of experiment compared to a simple study requiring 5 consecutive clonogenic assays. Moreover, it should be noticed that for more complex combinations comparing more NPs, cells, sources, the accelerated process would not last much longer, whereas the usual process duration would be drastically extended.
This article addresses the in silico–in vitro prediction issue of NP-based radiosensitization enhancement. Conversely to previous studies, the goal is neither to predict the X-ray dose effect nor the surviving fraction of irradiated cell but to carry out computational experiments to quickly identify non-efficient nanostructures and then to preferentially select the most promising ones for the subsequent in vitro and in vivo studies. To this aim, this article presents a computational ranking method and tests it on 3 different NPs by comparison with a standard Monte Carlo simulation not taking the biodistribution of NPs into account (scenario A) and the reference in vitro responses. The latter established the following ranking (from the best radiosensitizing NPs to the worse): 20 nm iron PVP, 20 nm gold PVP and 50 nm gold PEG. As the classical Monte Carlo method led us to the opposite ranking, the accelerated in silico method that we proposed accurately predicted the reference results. That corroborates the relevance of such a prior ranking method able to speed up the preclinical development of NPs in radiation therapy.
Acknowledgments
This work was supported by the research funds of the French Ligue Nationale Contre le Cancer, Région Lorraine and Euronanomed II project PhotoBrain. We would like to thank the microscopy platform “Service Commun de Microscopie” (Université de Lorraine, Campus Biologie Santé, Vandoeuvre-lès-nancy, France) and the Institut Lumière Matière (UMR 5306, Villeurbanne, France) for their highly appreciated help in the measurement of TEM and ICP-OES data.
Disclosure
The authors report no conflicts of interest in this work.
References
Coulter JA, Hyland WB, Nicol J, Currell FJ. Radiosensitising nanoparticles as novel cancer therapeutics – pipe dream or realistic prospect? Clin Oncol (R Coll Radiol). 2013;25(10):593–603. | ||
Cooper DR, Bekah D, Nadeau JL. Gold nanoparticles and their alternatives for radiation therapy enhancement. Front Chem. 2014;2:86. | ||
Jain S, Hirst DG, O’Sullivan JM. Gold nanoparticles as novel agents for cancer therapy. Br J Radiol. 2012;85(1010):101–113. | ||
Etheridge ML, Campbell SA, Erdman AG, Haynes CL, Wolf SM, McCullough J. The big picture on nanomedicine: the state of investigational and approved nanomedicine products. Nanomedicine. 2013;9(1):1–14. | ||
Marill J, Anesary NM, Zhang P, et al. Hafnium oxide nanoparticles: toward an in vitro predictive biological effect? Radiat Oncol. 2014;9:150. | ||
Douglass M, Bezak E, Penfold S. Monte Carlo investigation of the increased radiation deposition due to gold nanoparticles using kilovoltage and megavoltage photons in a 3D randomized cell model. Med Phys. 2013;40(7):071710. | ||
Jones BL, Krishnan S, Cho SH. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Med Phys. 2010;37(7):3809–3816. | ||
Lechtman E, Chattopadhyay N, Cai Z, Mashouf S, Reilly R, Pignol JP. Implications on clinical scenario of gold nanoparticle radiosensitization in regards to photon energy, nanoparticle size, concentration and location. Phys Med Biol. 2011;56(15):4631–4647. | ||
Lechtman E, Mashouf S, Chattopadhyay N, et al. A Monte Carlo-based model of gold nanoparticle radiosensitization accounting for increased radiobiological effectiveness. Phys Med Biol. 2013;58(10):3075–3087. | ||
Agostinelli S, Allison J, Amako K, et al. Geant4 – a simulation toolkit. Nucl Instrum Meth A. 2003;506(3):250–303. | ||
Baro J, Sempau J, Fernandez-Varea JM, Salvat F. PENELOPE: an algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl Instrum Meth B. 1995;100(1):31–46. | ||
Forster RA, Godfrey TNK. MCNP – a general Monte Carlo code for neutron and photon transport. In: Alcouffe R, Dautray R, Forster A, Ledanois G, Mercier B, editors. Monte-Carlo Methods and Applications in Neutronics, Photonics and Statistical Physics. Vol. 240. Berlin, Heidelberg: Springer; 1985:33–55. | ||
Rogers DW, Faddegon BA, Ding GX, Ma CM, We J, Mackie TR. BEAM: a Monte Carlo code to simulate radiotherapy treatment units. Med Phys. 1995;22(5):503–524. | ||
Butterworth KT, McMahon SJ, Taggart LE, Prise KM. Radiosensitization by gold nanoparticles: effective at megavoltage energies and potential role of oxidative stress. Transl Cancer Res. 2013;2(4):269–279. | ||
McMahon SJ, Prise KM, Currell FJ. Comment on ‘implications on clinical scenario of gold nanoparticle radiosensitization in regard to photon energy, nanoparticle size, concentration and location’. Phys Med Biol. 2012;57(1):287–290; discussion 291–285. | ||
Rima W, Sancey L, Aloy MT, et al. Internalization pathways into cancer cells of gadolinium-based radiosensitizing nanoparticles. Biomaterials. 2013;34(1):181–195. | ||
Stefancikova L, Porcel E, Eustache P, et al. Cell localisation of gadolinium-based nanoparticles and related radiosensitising efficacy in glioblastoma cells. Cancer Nanotechnol. 2014;5(1):6. | ||
Retif P, Pinel S, Toussaint M, et al. Nanoparticles for radiation therapy enhancement: the key parameters. Theranostics. 2015;5(9):1030–1044. | ||
Kodiha M, Wang YM, Hutter E, Maysinger D, Stochaj U. Off to the organelles – killing cancer cells with targeted gold nanoparticles. Theranostics. 2015;5(4):357–370. | ||
Cho SH, Krishnan S. Cancer Nanotechnology: Principles and Applications in Radiation Oncology. CRC Press; 2013. | ||
Martinov M, Thomson R. SU-E-T-667: radiosensitization due to gold nanoparticles: a Monte Carlo cellular dosimetry investigation of an expansive parameter space. Med Phys. 2015;42(6):3490. | ||
Elzey S, Tsai DH, Rabb SA, Yu LL, Winchester MR, Hackley VA. Quantification of ligand packing density on gold nanoparticles using ICP-OES. Anal Bioanal Chem. 2012;403(1):145–149. | ||
Franken NA, Rodermond HM, Stap J, Haveman J, van Bree C. Clonogenic assay of cells in vitro. Nat Protoc. 2006;1(5):2315–2319. | ||
Sancey L, Kotb S, Truillet C, et al. Long-term in vivo clearance of gadolinium-based AGuIX nanoparticles and their biocompatibility after systemic injection. ACS Nano. 2015;9(3):2477–2488. | ||
Ding GX. Energy spectra, angular spread, fluence profiles and dose distributions of 6 and 18 MV photon beams: results of Monte Carlo simulations for a Varian 2100EX accelerator. Phys Med Biol. 2002;47(7):1025–1046. | ||
Brun R, Rademakers F. ROOT – an object oriented data analysis framework. Nucl Instrum Meth A. 1997;389(1–2):81–86. | ||
Schneider CA, Rasband WS, Eliceiri KW. NIH image to ImageJ: 25 years of image analysis. Nat Methods. 2012;9(7):671–675. | ||
Foundation for Statistical Computing. R: A Language and Environment for Statistical Computing [Computer Program]. Vienna, Austria: R Foundation for Statistical Computing; 2015. | ||
Mesbahi A, Jamali F, Garehaghaji N. Effect of photon beam energy, gold nanoparticle size and concentration on the dose enhancement in radiation therapy. Bioimpacts. 2013;3(1):29–35. | ||
Zhang DG, Feygelman V, Moros EG, Latifi K, Zhang GG. Monte Carlo study of radiation dose enhancement by gadolinium in megavoltage and high dose rate radiotherapy. PLoS One. 2014;9(10):e109389. | ||
Tsiamas P, Liu B, Cifter F, et al. Impact of beam quality on megavoltage radiotherapy treatment techniques utilizing gold nanoparticles for dose enhancement. Phys Med Biol. 2013;58(3):451–464. |
 © 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.