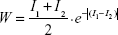Back to Journals » Clinical Interventions in Aging » Volume 10
Modeling clustered activity increase in amyloid-beta positron emission tomographic images with statistical descriptors
Authors Shokouhi S, Rogers B, Kang H , Ding Z, Claassen D, Mckay J, Riddle W
Received 3 February 2015
Accepted for publication 19 February 2015
Published 20 April 2015 Volume 2015:10 Pages 759—770
DOI https://doi.org/10.2147/CIA.S82128
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Richard Walker
Sepideh Shokouhi,1 Baxter P Rogers,1 Hakmook Kang,2 Zhaohua Ding,1 Daniel O Claassen,3 John W Mckay,1 William R Riddle1
On behalf of the Alzheimer’s Disease Neuroimaging Initiative
1Department of Radiology and Radiological Sciences, Vanderbilt University Institute of Imaging Science, 2Department of Biostatistics, 3Department of Neurology, Vanderbilt University, Nashville, TN, USA
Background: Amyloid-beta (Aβ) imaging with positron emission tomography (PET) holds promise for detecting the presence of Aβ plaques in the cortical gray matter. Many image analyses focus on regional average measurements of tracer activity distribution; however, considerable additional information is available in the images. Metrics that describe the statistical properties of images, such as the two-point correlation function (S2), have found wide applications in astronomy and materials science. S2 provides a detailed characterization of spatial patterns in images typically referred to as clustering or flocculence. The objective of this study was to translate the two-point correlation method into Aβ-PET of the human brain using 11C-Pittsburgh compound B (11C-PiB) to characterize longitudinal changes in the tracer distribution that may reflect changes in Aβ plaque accumulation.
Methods: We modified the conventional S2 metric, which is primarily used for binary images and formulated a weighted two-point correlation function (wS2) to describe nonbinary, real-valued PET images with a single statistical function. Using serial 11C-PiB scans, we calculated wS2 functions from two-dimensional PET images of different cortical regions as well as three-dimensional data from the whole brain. The area under the wS2 functions was calculated and compared with the mean/median of the standardized uptake value ratio (SUVR). For three-dimensional data, we compared the area under the wS2 curves with the subjects’ cerebrospinal fluid measures.
Results: Overall, the longitudinal changes in wS2 correlated with the increase in mean SUVR but showed lower variance. The whole brain results showed a higher inverse correlation between the cerebrospinal Aβ and wS2 than between the cerebrospinal Aβ and SUVR mean/median. We did not observe any confounding of wS2 by region size or injected dose.
Conclusion: The wS2 detects subtle changes and provides additional information about the binding characteristics of radiotracers and Aβ accumulation that are difficult to verify with mean SUVR alone.
Keywords: amyloid-beta plaques, positron emission tomography, 11C-Pittsburgh compound B, statistical descriptors, two-point correlation function
Introduction
The presence of amyloid-beta (Aβ) plaques in the cortical gray matter is among the major pathological features of Alzheimer’s disease (AD), and is present years before memory decline and other clinical manifestations emerge.1–7 Reliable diagnostic and prognostic information in the early stages of AD is necessary for clinical interventions that can halt disease progression. More so, there exists a substantial need for quantitative imaging techniques that can sensitively monitor changes in amyloid status over time and determine the response to therapeutic interventions. Aβ plaques have been imaged in the human brain using positron emission tomography (PET) with radiotracers, such as 11C-Pittsburgh compound B (11C-PiB)8 and 18F-florbetapir.9 In an attempt to quantify levels of in vivo amyloid plaque, contemporary analyses rely on the calculation defined as the ratio of image intensity between the cortex and a reference region (commonly the cerebellar gray matter). This method, the standardized uptake value ratio (SUVR), is appealing due to its computational simplicity and short scan time. Radiotracer uptake is measured after binding in the cortex and reference region reaches a steady state 40–50 minutes after injection.3 Healthy cortex typically shows tracer binding at an SUVR of 1.5 or less. Any ratio above this threshold is referred to as “PiB-positive” and is thought to be indicative of abnormal accumulation of Aβ plaques. Another method employs kinetic modeling of amyloid-PET, and is computed from dynamic data10,11 collected over a longer acquisition time, but is more susceptible to subject movement. Both the SUVR and the kinetic modeling methods typically rely on the mean or median of the voxel activity values across a region of interest, but fail to account for variations in the spatial pattern within the region. Consequently, regional SUVR mean values are subject to high variance (large error bars), thus precluding an accurate assessment of longitudinal alterations to Aβ accumulation. Therefore, there exists a need for image analysis methods that can characterize spatial patterns of radiotracer activity in Aβ-PET data to provide additional information about longitudinal alteration in distribution of radiotracer activity and Aβ accumulation.
Statistical descriptors such as the two-point correlation function (S2) are commonly used in specialties such as material science and astronomy to characterize microscopic properties of materials or galaxy distributions.12–20 This metric provides a detailed characterization of spatial patterns in images, typically referred to as clustering or flocculence. Continuous-valued Aβ-PET images are analogous to the material science concept of multiphase media where different voxel activity values correspond to different phases. Conventional two-point correlation analysis would require the computation of S2 functions for each voxel value, which is difficult to interpret due to the broad range of activity values within the PET data. In this study, we applied a modified S2 metric, a weighted two-point correlation function (wS2), on continuous-valued (nonbinary) 11C-PiB PET to capture longitudinal changes in image spatial patterns with a single statistical function. Here, we introduce a novel computational framework of the wS2 analysis. We then implement this analysis on longitudinal 11C-PiB scans in human subjects and compare the outcomes of wS2 with currently used mean/median SUVR and cerebrospinal fluid (CSF) measures of Aβ.
Material and methods
Calculation of two-point correlation function
Calculation of S2 involves comparison of each voxel with all other voxels within the image. This process can be approximated by selecting N number of random voxel pairs on a binary image space (voxel values are either 1 or 0) with variable intervoxel distances and counting the number of times both voxel values are equal to 1 (true instances). The instances are then binned by the intervoxel distances, and for a given distance r, the number of true instances is divided by the total number of instances with distance r. Figure 1 illustrates two binary images with a spatially random distribution of nonzero voxels and their corresponding two-point correlation functions. The two-point correlation function can be interpreted as the probability that two randomly selected image voxels x1 and x2 both are nonzero. The x axis of the plot in Figure 1 represents the intervoxel distance and the y axis shows the calculated S2 values for the given distance. The two images in Figure 1 are not identical but are statistically similar, thus generating similar S2 curves. Figure 2 shows another set of binary images with the same number of nonzero (black) voxels. While in the first image (Figure 2A) these voxels are randomly distributed, in the second image (Figure 2B) some of them were moved around to form small clusters of 4–5 voxels. The clustering effect changes the S2 function of the second image (dashed line). The area under the curve (AUC) increases with the increase of flocculence (clustering) in the spatial distribution of black voxels. Similarly, more changes in S2 function can be observed when the flocculence increases (Figure 2C). Since all three images have the same fraction of nonzero voxels, their calculated mean voxel values remain unchanged. Therefore, the utilization of the two-point correlation function can reveal additional information about the spatial distribution of the voxel values, which cannot be determined by their calculated mean or median values.
Calculation of weighted two-point correlation function
Continuous-valued images such as an amyloid-PET can be characterized with multiple two-point correlation functions, one for each voxel value.20 However, typical amyloid-PET images have more than a few activity values. Therefore, such an approach would require computation of a large number of S2 functions, which is not only computationally intensive but also the results are difficult to interpret. To address this challenge, we formulated a weighted two-point correlation function (wS2) to facilitate implementation of a single statistical function on a nonbinary image. Similar to S2, wS2 is estimated by randomly selecting N pairs of voxels at variable distances on the image space. For S2, each instance is weighted either zero (when one or both voxels are zero) or one (when both voxels are nonzero). For wS2, we generalize this by computing a weighting factor that preferentially weights instances where both voxels have high activity. We used the following equation as an initial approach in defining a weighting scheme:
| (1) |
The weighting factor for each instance, W, is calculated as the product of two terms. The first term is the average value of the two selected voxels (I1, I2). The second term incorporates the absolute difference between the two voxel values into an exponential decay. This weighting scheme takes advantage of the information encoded by the image intensities. Figure 3 illustrates the weighting schemes in S2 for binary images and in wS2 for nonbinary images. Figure 4 shows the weighted two-point correlation functions of three simulated nonbinary images. The AUC and the slope changes with the clustered increase of activity from the upper image (Figure 4A) to the lower image (Figure 4C). Implemented on amyloid-PET images, the wS2 can be used to capture the flocculence of the tracer activity within different cortical regions. While several factors, such as the nonspecific radiotracer binding, partial volume effect, and white matter retention contribute to the activity pattern within a region of a PET image, we hypothesize that the observed clustering of the activity distribution and the spread of high-activity clusters could be partially attributed to underlying heterogeneity in the spatial distribution of Aβ plaques and the specific binding of the radiotracer. The presence of regional activity clusters in longitudinal PET data is often qualitatively visible, as shown in Figure 5, with images of 11C-PiB in four different regions of three Alzheimer’s Disease Neuroimaging Initiative (ADNI) subjects. The regional activity distribution of baseline images (Figure 5A, C, E, and G) were compared with their follow-up time points (Figure 5B, D, F, and H). All images show localized patterns of high activity clusters, which seem to remain in the same area within the course of one or 2 years. With the weighted two-point correlation functions, we can define a quantitative metric that characterizes the clustered increase of activity in different regions or in the whole brain. The next sections of this study provide details on 11C-PiB PET acquisition and preprocessing, as well as implementation of wS2 on two-dimensional and three-dimensional PET data and evaluation.
Subjects
Data used in the preparation of this paper were obtained from the ADNI database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the US Food and Drug Administration, private pharmaceutical companies, and non-profit organizations as a $60 million, 5-year public–private partnership. The primary goal of the ADNI has been to test whether serial magnetic resonance imaging (MRI), PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians in the development of new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The principal investigator of this initiative is Michael W Weiner, from the VA Medical Center and University of California-San Francisco. The ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the USA and Canada. The initial goal of the ADNI was to recruit 800 subjects, but the ADNI has been followed by ADNI-GO and ADNI-2. To date, these three protocols have recruited over 1,500 adults aged 55–90 years to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow-up duration of each group is specified in the protocols for ADNI-1, ADNI-2, and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.
We used 31 ADNI subjects from MCI, late mild MCI, and the old healthy control (normal) cohort. Table 1 summarizes the demographic and clinical data of the subjects used in this study. The subjects were selected based on the availability of longitudinal 11C-PiB scans. In addition to longitudinal PiB-PET scans, 13 subjects also had longitudinal CSF measures obtained at the same time points as the PiB scans. The ADNI UPENN-Longitudinal-Biomarker Data (4-year) file was searched to identify these subjects, whose PiB-PET data were used for three-dimensional analysis of the whole brain wS2 and its association with CSF Aβ. The remaining subjects who did not have complete biospecimen information were used for two-dimensional wS2 analysis of different brain regions and its association with region size and image noise.
  | Table 1 Clinical data for Alzheimer’s Disease Neuroimaging Initiative subjects used for this study |
Data acquisition and preprocessing
11C-PiB PET from baseline and follow-up scans together with T1-weighted MRI volumes were downloaded from the ADNI database. While some subjects had follow-up scans at both 12 months and 24 months after baseline, others had only one follow-up at either 12 months or 24 months. All PiB-PET scans were started 50 minutes after injection, allowing for tracer uptake and nonspecific washout. Four dynamic frames with a scan duration of 20 minutes were coregistered, averaged into a single image, and normalized with respect to cerebellar gray matter. All preprocessing steps were performed by the Laboratory of Neuroimaging at the University of Southern California. We downloaded the preprocessed PET data that were coregistered, averaged, and intensity-normalized to the cerebellar gray matter. In addition, we limited our PiB-PET data selection to those scans that were performed with the same scanner, acquisition protocol, and image reconstruction method at baseline and each follow-up to reduce variations due to scanner resolution or sensitivity.
wS2 analysis on two-dimensional data
For each subject we sampled axial PiB image slices from several different brain regions, including the occipital lobe and the bilateral temporal, parietal, and frontal lobes. The T1-weighted MRI volume was used to define these regions using the methods described by Riddle et al.21 Briefly, these anatomical regions were obtained by aligning the subject’s T1-weighted MRI volume (acquired at a time point close to the PiB PET baseline scan) with the T1-weighted MRI volume from a reference brain where the regions were segmented manually. The deformation field between the reference brain and the subject’s T1-weighted MRI volume was calculated with a nonrigid demons registration algorithm.22 The regional binary masks from the reference brain were warped to the subject’s image volume with the nonrigid deformation field. Each brain volume was also segmented into CSF, gray matter, and white matter with Fuzzy C-means23 and a gray matter mask was created for each anatomical region. These regional gray matter masks were applied to the PiB-PET images that were coregistered to the subject’s MRI volume in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). Altogether, we had over 300 sets of two-dimensional images that served as starting points for our two-dimensional analysis, which aimed to investigate the association between SUVR and wS2 in different regions and to determine whether the wS2 outcomes were biased by the region size, which was defined as the number of gray matter voxels within a region where the wS2 voxel pairs were sampled from. For the wS2 calculation, we generated 100,000 random voxel pairs located within the gray matter of that region. All instances were weighted using equation 1, binned by the Euclidean voxel distances r between zero and 10 mm, and divided by the number of instances for each distance to obtain the wS2(r). The error associated with the wS2 curves was calculated by resampling 20 ensembles of 100,000 voxel pairs and calculating the standard deviation. We found that additional resampling beyond 20 did not increase the error bars. The areas under the wS2 curves (AUC) from zero to 10 mm distance were used as quantitative values to characterize the increased clustered activity and how it related to changes in SUVR mean values. We implemented a linear mixed-effects model to determine the effect of the region size on wS2. We also utilized another statistical analysis to determine whether longitudinal changes in the regional wS2 curves were affected by differences in the administered radiotracer dose at baseline and follow-up time points. This was analyzed with mixed-effects models using the R software package (www.r-project.org). The AUC at the follow-up time points was predicted by baseline (time 0) AUC, time point (1 or 2), region size, and change in injection dose relative to baseline as fixed effects.
Three-dimensional wS2 analysis of whole brain
The whole brain PiB-PET images were aligned to the T1-weighted MRI image at a time point closest to the baseline PET. The gray matter mask of the whole brain T1-weighted MRI was overlaid with the PiB-PET. We generated 50,000 random voxel pairs located within the gray matter fraction of the PET images to calculate the wS2. The AUCs from zero to 15 mm distance were calculated and compared with the CSF measures obtained from the ADNI database. For the CSF measures, lumbar punctures were performed at the participating ADNI sites and are described in the ADNI biospecimen protocols (adni.loni.ucla.edu/research/protocols/biospecimens-protocols). The CSF Aβ1–42 was obtained from a multiplex xMAP Luminex platform using Innogenetics immunoassay kit-based reagent. Using the Spearman’s rank correlation, we calculated the correlation coefficients between the AUC of the wS2 curves and 1/Aβ. There is an inverse correlation between CSF Aβ and PET images. For convenience, we used 1/Aβ instead of Aβ to take away the negative sign from the correlation coefficient. Similarly, we calculated the correlation coefficients between the whole brain PiB-PET SUVR mean and median values and the CSF Aβ measures. In addition to Spearman’s correlation, we utilized a linear mixed-effects (AR1) model to evaluate temporal correlations between wS2, SUVR mean and SUVR median (outcome variables) and CSF Aβ (predictor).
Results
wS2 analysis on two-dimensional data
The implementation of wS2 on two-dimensional images not only offered a visual comparison of this method with the observed qualitative changes in the PET data, but also allowed a comparison between wS2 and SUVR mean values in different brain regions. Figure 6 shows a sample 11C-PiB image from a subject’s right temporal lobe at baseline (Figure 6A) and follow-up (Figure 6B). Figure 6C shows the calculated SUVR mean values of the images at baseline and follow-up, and Figure 6D shows their corresponding wS2 curves. Both the SUVR mean and the wS2 method indicate little change between baseline and follow-up. For comparison, Figure 7 shows the 11C-PiB images from another subject’s left parietal lobe at baseline (Figure 7A) and follow-up (Figure 7B). Figure 7C shows the calculated SUVR mean values at baseline and follow-up. Due to the large error bars, it is difficult to determine whether there is a significant change in the SUVR mean. In comparison with the SUVR mean value, the wS2 curves at the two time points (Figure 7D) are clearly separated. For the group level, the Spearman’s rank correlation between the wS2 and SUVR mean is 0.9 with P<0.001. We used a linear mixed-effects model analysis to determine whether longitudinal changes in the wS2 curves were affected by region size or differences in the radiotracer dose administered at baseline and follow-up time points. The outcomes of this analysis are summarized in Table 2. For the effect of region size on AUC, we obtained a P-value of 0.61, indicating that the size of the region from where the voxel pair was sampled does not affect the wS2 outcomes. For the effect of differences in injected dose between the baseline and follow-up scan, we obtained a P-value of 0.28, indicating no significant effect.
Three-dimensional wS2 analysis on whole brain
The visit-to-visit association between the whole brain AUCs of wS2 and the CSF 1/Aβ were calculated using the Spearman’s correlation coefficient. The outcomes were compared with the correlation between the SUVR mean/median values and CSF measures at baseline and 12-month follow-up. All correlation outcomes are summarized in Table 3. We found a slightly higher inverse correlation between wS2 and CSF Aβ. These were 0.82 for baseline and did not change significantly (0.8) after 12 months. For comparison, the correlation between the SUVR mean and CSF Aβ decreased from 0.83 to 0.6 after 12 months. Similarly, the correlation between SUVR median value and CSF Aβ decreased from 0.83 to 0.6. We also utilized a linear mixed-effects (AR1) model as an additional method to evaluate temporal correlations between wS2, SUVR mean and SUVR median (outcome variables) and CSF Aβ (predictor). Based on this model, we observed similarly significant inverse correlation between CSF Aβ and all three brain PET measures. These were 0.45 (P=0.005) for wS2, 0.45 (P=0.008) for SUVR mean, and 0.39 (P=0.02) for SUVR median.
Discussion
This is the first study that implements two-point correlation functions to detect longitudinal changes in Aβ-PET data. We formulated a weighted two-point correlation to characterize the clustered activity increase of 11C-PiB PET images and its association with CSF outcomes and SUVR mean values. We used a weighting function that preferentially weights instances where both voxels have high activity as an initial approach for implementing a single correlation function on continuous-valued amyloid-PET data. All PET data were normalized to the cerebellum gray matter, allowing utilization of a simple weighting scheme for wS2. The objective of this study was to validate the wS2 technique. In the future, we will implement this method on amyloid-PET data that are not normalized by the cerebellum or any other reference region, thus minimizing potential errors associated with reference tissue normalizations. The wS2 approach on non-normalized PET data would require more thoroughly evaluated weighting functions, which we intend to explore further. We used the area under the wS2 function as a quantitative outcome of this method. Other characteristic features, such as the shape or the temporal slope of the wS2 function, may be used as additional quantitative parameters to characterize longitudinal changes, particularly for non-normalized amyloid-PET data. Similar to the SUVR mean analysis, the wS2 approach can be performed on static PET scans and does not require long dynamic acquisitions. The wS2 metric has some characteristics that offer potential advantages over the conventional typical SUVR mean value. It is associated with smaller variance (error bars), which is particularly useful for clinicians who are interested in detecting small changes in longitudinal amyloid-PET as a response to therapeutic interventions. The large error bars of the SUVR mean value often make it difficult to detect subtle changes, and the wS2 analysis can provide additional information to assess for possible alterations. Implemented on an AD cohort, the two-point correlation function could be used to determine whether amyloid accumulation remains static in the AD phase. The wS2 method could be also utilized as a useful tool to compare the regional patterns of activity distribution between different amyloid-PET radiotracers in the same subject and gain more insight into differences in radiotracer binding characteristics. As the P-values in Table 2 indicate, we did not see any significant effect on AUC related to region size or dose injected. The injected dose was used as a surrogate for image noise to determine whether possible noise mismatches between baseline and follow-up scans would be considered as confounding factors in the wS2 analysis. While differences in scanner sensitivity also contribute to the noise, we were able to disregard the scanner effect by selecting PiB-PET data that were performed with the same scanner at baseline and follow-up. The objective of our three-dimensional whole brain wS2 analysis was to compare the AUC outcomes with the CSF measures of Aβ1–42, which are known biomarkers of AD pathology. The decrease in CSF Aβ1–42 is associated with increased activity in 11C-PiB PET images, as investigated by several previous studies.24–28 The correlation coefficients between the SUVR mean and the CSF Aβ1–42 from our study were also comparable with those in a previous study by Forsberg et al26 investigating the relationship between PiB retention and CSF Aβ1–42 in an MCI cohort. Comparing the wS2 method with the conventional SUVR mean and median values (Table 2), we were able to show a slightly higher inverse correlation between the PiB imaging data and CSF Aβ. Overall, the wS2 technique can detect subtle changes in the spatial pattern of PiB-PET and efficiently reduce the complexity of implementing statistical descriptors on continuous-valued images. The weighed two-point correlation technique can be easily adapted for other imaging modalities, such as computed tomography or MRI for a wide range of applications in medicine and biology.
Acknowledgments
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) via the National Institutes of Health (grant U01 AG024904) and Department of Defense (award W81XWH-12-2-0012). The ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the Alzheimer’s Association, Alzheimer’s Drug Discovery Foundation, Araclon Biotech, BioClinica, Inc, Biogen Idec Inc, Bristol-Myers Squibb Company, Eisai Inc, Elan Pharmaceuticals, Inc, Eli Lilly and Company, EuroImmun, F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc, Fujirebio, GE Healthcare, IXICO Ltd, Janssen Alzheimer Immunotherapy Research and Development, LLC, Johnson & Johnson Pharmaceutical Research and Development LLC, Medpace, Inc, Merck & Co., Inc, Meso Scale Diagnostics, LLC, NeuroRx Research, Neurotrack Technologies, Novartis Pharmaceuticals Corporation, Pfizer Inc, Piramal Imaging, Servier, Synarc Inc, and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. This study was supported by NIH/NIBIB grants R00 EB 009106 (to SS) and K23 NS080988 (to DC).
The authors would like to thank John Gore, Todd Peterson, Noor Tantawy, Harrison Barrett, Antonio Sastre, Salvatore Torquato, Andreas Berlind, Kristen Nelson, and Philip Crooke for their supportive discussions, Lucy Qu and Hyeyon Kim for helping with the data analysis, and Benoit M Dawant and Rui Li for the providing the rigid and demons registration software.
Data used in preparation of this article were obtained from the ADNI database (adni.loni.usc.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp- content/uploads/how_to_apply/ADNI_Acknowledgement _List.pdf.
Disclosure
The authors report no conflicts of interest in this work.
References
Hardy J, Selkoe DJ. The amyloid hypothesis of Alzheimer’s disease: progress and problems on the road to therapeutics. Science. 2002;297:353–356. | ||
McKhann GM, Knopman DS, Chertkow H, et al. The diagnosis of dementia due to Alzheimer’s disease: recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimers Dement. 2011;7:263–269. | ||
Rowe CC, Ng S, Ackermann U, et al. Imaging beta-amyloid burden in aging and dementia. Neurology. 2007;68:1718–1725. | ||
Rowe CC, Ellis KA, Rimajova M, et al. Amyloid imaging results from the Australian Imaging, Biomarkers and Lifestyle (AIBL) study of aging. Neurobiol Aging. 2010;31:1275–1283. | ||
Morris JC, Roe CM, Grant EA, et al. Pittsburgh compound B imaging and prediction of progression from cognitive normality to symptomatic Alzheimer disease. Arch Neurol. 2009;66:1469–1475. | ||
Thal DR, Rüb U, Orantes M, Braak H. Phases of A beta-deposition in the human brain and its relevance for the development of AD. Neurology. 2002;58:1791–1800. | ||
Rabinovici GD, Rosen HJ, Alkalay A, et al. Amyloid vs FDG-PET in the differential diagnosis of AD and FTLD. Neurology. 2011;77:2034–2042. | ||
Klunk WE, Engler H, Nordberg A, et al. Imaging brain amyloid in Alzheimer’s disease with Pittsburgh compound-B. Ann Neurol. 2004;55:306–319. | ||
Choi SR, Golding G, Zhuang ZP, et al. Preclinical properties of 18F-AV-45: a PET agent for Aβ plaques in the brain. J Nucl Med. 2009;50:1887–1894. | ||
Logan J, Fowler JS, Volkow ND, Wang GJ, Ding YS, Alexoff DL. Distribution volume ratios without blood sampling from graphical analysis of PET data. J Cereb Blood Flow Metab. 1996;16:834–840. | ||
Price JC, Klunk WE, Lopresti BJ, et al. Kinetic modeling of amyloid binding in humans using PET imaging and Pittsburgh compound-B. J Cereb Blood Flow Metab. 2005;25:1528–1547. | ||
Torquato S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties. New York, NY, USA: Springer-Verlag; 2002. | ||
Yeong CL, Torquato S. Reconstructing random media. Phys Rev E Stat Nonlin Soft Matter Phys. 1998;57:495. | ||
Jiao Y, Stillinger FH, Torquato S. Modelling heterogeneous material via two-point correlation functions: basic principles. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76:031110. | ||
Debye P, Anderson HR. The correlations function and its application. J Appl Phys. 1957;28:679. | ||
Peebles PJE. The Large Scale Structure of the Universe. Princeton, NJ, USA: Princeton University Press; 1980. | ||
Rivolo AR. The two-point galaxy correlation function of the Local Supercluster. Astrophys J. 1986;301:70–76. | ||
Dalton GB, Efstathiou G, Sutherland WJ, Maddox SJ, Davis M. The two-point correlation function of rich clusters of galaxies: results from an extended APM cluster redshift survey. Mon Not R Astron Soc. 1994;271:L47. | ||
Blair SC, Berge PA, Berryman JG. Using two-point correlation functions to characterize microgeometry and estimate permeabilities of sandstones and porous glass. J Geophys Res. 1996;101(B9):20359–20375. | ||
Cooper L, Saltz J, Machiraju R, Huang K. Two-point correlation as a feature for histology images: feature space structure and correlation updating. Conf Comput Vis Pattern Recognit Workshops. 2010:79–86. | ||
Riddle WR, DonLevy SC, Wushensky CA, Dawant BM, Fitzpatrick JN, Price RR. Quantifying cerebral changes in adolescence with MRI and deformation based morphometry. J Magn Reson Imaging. 2008;28:320–326. | ||
Dawant BM, Hartmann SL, Thirion JP, Maes F, Vandermeulen D, Demaerel P. Automatic 3-D segmentation of internal structures of the head in MR images using a combination of similarity and free-form transformations. Part I, Methodology and validation on normal subjects. IEEE Trans Med Imaging. 1999;18:909–916. | ||
Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans Med Imaging. 1999;18:737–752. | ||
Tolboom N, van der Flier WM, Yaqub M, et al. Relationship of cerebrospinal fluid markers to 11C-PiB and 18F-FDDNP binding. J Nucl Med. 2009;50:1464–1470. | ||
Landau SM, Lu M, Joshi AD, et al; Alzheimer’s Disease Neuroimaging Initiative. Comparing positron emission tomography imaging and cerebrospinal fluid measurements of β-amyloid. Ann Neurol. 2013;74:826–836. | ||
Forsberg A, Engler H, Almkvist O, et al. PET imaging of amyloid deposition in patients with mild cognitive impairment. Neurobiol Aging. 2008;29:1456–1465. | ||
Fagan AM, Mintun MA, Mach RH, et al. Inverse relation between in vivo amyloid imaging load and cerebrospinal fluid Abeta42 in humans. Ann Neurol. 2006;59:512–519. | ||
Koivunen J, Pirttilä T, Kemppainen N, et al. PET amyloid ligand [11C]PiB uptake and cerebrospinal fluid beta-amyloid in mild cognitive impairment. Dement Geriatr Cogn Disord. 2008;26:378–383. |
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.