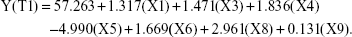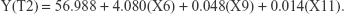Mathematical evaluation of the influence of multiple factors on implant stability quotient values in clinical practice: a retrospective study

Introduction

Since the pioneering work of Branemark in 1952,¹ dental implants have become a widely used treatment option in the past few decades. Dental implants are used to provide mechanical support for various dental prostheses, such as crowns, bridges, dentures, and orthodontic apparatuses. The basis for such a desired support function by an implant is its mechanical stability. This is generally described, as a function of time, as a primary and a secondary stability. The primary stability is largely based on an immediate mechanical anchoring of the implant in the surrounding bone upon surgical implantation. The secondary stability is achieved by a biological healing process – called osseointegration – and it forms a direct structural and functional connection between the implant and the neoformed surrounding bone tissues, without any interpositioned connective tissue.² In clinical practice, the degree of implant stability is considered to be an important parameter to estimate the scope of mechanical loading capability and to provide baseline information as a tool to assess the clinical outcome and time course.³

A large number of efforts have been made to identify and to develop novel techniques for the quantitative assessment of the implant stability. An ideal technique should be simple, noninvasive, and clinician friendly. One of the candidate techniques is Periotest.^4,5 However, the Periotest readings do not always correspond precisely to a biomechanical parameter, since they are strongly related to the excitation direction and position.^4,6 As an alternative, resonance frequency analysis (RFA) was proposed to estimate implant stability in 1996.^7,8 RFA is performed using a small transducer that is fastened to implants/abutments. This transducer has a vertical beam that is attached using two piezoceramic elements. One piezoceramic element produces a vibration consisting of a small sinusoidal signal in the range of 5–15 kHz in steps of 25 Hz and the other element analyzes the response of the transducer to the vibration.⁸ The peak amplitude of the response is coded into a parameter called the implant stability quotient (ISQ). ISQ values range from 0 (indicating a totally mobile implant) to 100 (indicating a perfectly stable implant–bone complex).⁹ The ISQ value is positively correlated to the mechanical stability of an implant. RFA is a noninvasive technique and shows a high reproducibility of results.^10,11 In recent years, RFA has become one of the most widely used techniques to assess stability on the spot in order to determine the possible loading occasion and to assess the long-term survival of dental implants.¹² ISQ values ranging from 60 to 80 are widely accepted as a standard for achieving primary stability.^13–15 In the clinic, ISQ values of at least 55 at the time of implant placement might be considered as representing clinically relevant stability and possible predictors of successful osseointegration.^13,15 As for immediate implant loading, an ISQ measure of 60–65 will ensure a good prognosis.¹⁶

Attempts to achieve early functionality of implants have been continuously pursued in the field of oral implantology. Immediate implantation is associated with several advantages, such as the reduction of surgical trauma, the shortening of the treatment time, and the improved preservation of surrounding bone and soft tissue. In cases with sufficient primary stability, evidence is presented in the literature that immediate implantation (or even immediate loading) yields equal efficacy in terms of long-term success and esthetic outcome compared to delayed implantation.¹⁷ However, the technique of immediate implantation is still a challenge with respect to achieving sufficient primary stability of the implant that, if not achieved, may lead to a higher implant failure rate.¹⁸ Careful case selection must be performed to avoid treatment failures and esthetic complications when deciding between immediate and delayed implant placements.¹⁸ Therefore, it is also of great significance to estimate the case-specific ISQ values in order to create a detailed treatment plan. For this purpose, continuous efforts are made to elucidate the influence of various factors on ISQ values using the RFA technique. In previous studies, some of the factors that were investigated that possibly influence the ISQ values are implant design,⁹ insertion torque,¹⁹ immediate/delayed implantation,²⁰ drilling design,^21,22 bone density,²³ bone grafting, and mechanical loading pattern.²⁴ Most of these studies demonstrated a significant influence of such factors on the basis of the assessment of the relationship between ISQ values and single and/or several factors. Albeit so, the weight coefficients of the various influencing factors for the ISQ values remained unrevealed, so that most of the decisions made by clinicians are still made largely based on practical experience. A mathematical model may play a critical role to thoroughly assess the individual contribution of the various factors on ISQ values in clinical situations by performing multivariate analyses. Hitherto, there is still a lack of such an adequate mathematical model.

In this study, we retrospectively analyzed both the demographic and clinical data of 329 implants from 177 patients by using a multivariate linear regression analysis. We wished to determine the contribution of each of the individual factors to the ISQ values in a clinical set up in order to provide baseline data for the creation of a mathematical model to estimate the likely ISQ value for an individual case.

Patients and methods

Patients and implants

The conduct of this study was approved by the Review Board of the Best & Easy Dental Clinic, People’s Republic of China. It is routine for all patients at the Best & Easy Dental Clinic to give an informed written consent for potential inclusion in clinical studies. In this retrospective study, we reviewed the data of all the patients who received implant treatment in the Best & Easy Dental Clinic, Hangzhou, People’s Republic of China, from 2012 to 2015. SICace implants (SIC Invent AG, Basel, Switzerland) with different diameters and lengths were used. All the implants were placed by the same surgeon. In total, 178 patients with 331 implants were included in the study. There were two implant failures (the failure rate was 0.6%) over this time period. The data of these two implants were not included in the following analysis.

General inclusion and exclusion criteria for implant treatments

In the Best & Easy Dental Clinic, we used the American Society of Anesthesiologist (ASA) classifications (ASA1, ASA2, and ASA3) to evaluate the systemic health status of patients for establishing the inclusion criteria for implant treatment.²⁵ Briefly, well-controlled status of the patient in case of systemic disease (to tolerate the surgery) was considered. Regarding the oral health, patients with only mild and/or moderate (but well controlled) periodontitis and patients with a good oral hygiene status were included. Patients were excluded from implant surgery if they were pregnant or would be unable to withstand the stress of dental implant surgery (ASA4–5). Patients were also excluded if they had severe/uncontrolled periodontitis.

Patient records

We retrospectively collected the following data from patients: potential candidate factors possibly influencing the ISQ values: (X1) sex, (X2) age, (X3) maxillar/mandibular location, (X4) immediate/delayed implantation, (X5) presence or absence of bone grafting, (X6) implant diameter, (X7) implant length, (X8) I/II-stage healing pattern, (X9) insertion torque, (X10) bone type, and (X11) T1–T2 time interval.

According to the record of implantation procedure, the II-stage healing pattern was used only if the insertion torque was <20 N or the ISQ value <65. The bone type of the implant sites was categorized into types I, II, III, and IV according to the classification of Lekholm and Zarb.²⁶

The ISQ values (measured with Osstell™ Mentor; Integration Diagnostic Ltd., Goteborg, Sweden) were recorded from the mesial, distal, lingual, and buccal sites of each implant at both T1 (immediately after implantation) and T2 (immediately before restoration and loading). Typically, after 6–12 weeks, patients received the restoration therapy. In a few cases, the patients received the restoration/loading therapy as late as 1 year.

Statistical analysis

Initially, we used the Kruskal–Wallis test to compare the ISQ values from the mesial, distal, lingual, and buccal sites of implants at T1 and T2. We used paired t-tests to assess the difference in ISQ values at T1 and T2 for either immediately placed or delayed placed implants. We also applied paired t-tests to assess the influence of immediate/delayed implantation on ISQ values at T1 or T2. Thereafter, we performed multivariate linear regression analyses to determine the weight coefficients of the eleven candidate factors possibly influencing the ISQ values at both T1 and T2 time points. All the statistical analyses were performed using an SPSS^® 21.0 software (SPSS Inc., Chicago, IL, USA). Level of significance was set at P<0.05, and the confidence level at 95%.

In the multivariate linear regression analysis, the categories of the influencing factors were transformed into numbers as follows: (X1) male =1, female =2; (X3) maxillary =1, mandible =2; (X4) immediate =1, delayed =2; (X5) bone grafting: no =1, yes =2; and (X8) I-stage =2, II-stage =1. Dummy variables were used for bone types (X10): type 1 =100, type 2 =010, type 3 =001, and type 4 =000. The numbers for the remaining factors were directly used for statistical analysis.

Results

A total of 329 implants from 177 patients were included in this study. The descriptive characteristics of all the patients and implants are listed in Table 1.

Table 1 Descriptive characteristics of the patients and implants

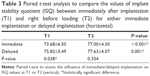
There were no significant differences among the ISQ values measured from the labial, lingual, distal, and mesial sites at the time points of either immediately after implantation (T1) or right before loading (T2; Table 2). For both immediate and delayed implantation, the ISQ values at T1 were significantly lower than those at T2 (Table 3). At T1, the ISQ values of immediately placed implants were significantly lower than those of delayed placed implants. At T2, there was no significant difference between the ISQ values of immediately placed implants and those of the delayed implants (Table 3).

Table 2 Kruskal–Wallis analysis to compare the values of implant stability quotient that were measured from the labial, lingual, distal, and mesial sites using resonance frequency analysis technique immediately after implantation (T1) and right before loading (T2), respectively Note: Data shown as mean ± standard deviation.

Table 3 Paired t-test analysis to compare the values of implant stability quotient (ISQ) between immediately after implantation (T1) and right before loading (T2) for either immediate implantation or delayed implantation (horizontal) Notes: Paired t-test to assess the influence of immediate/delayed implantation on ISQ values at T1 or T2 (vertical). *Statistically significant difference.

At T1, the multivariate linear regression analysis showed that the ISQ values were significantly influenced by the following seven factors: (X1) sex, (X3) maxillary/mandibular location, (X4) immediate/delayed implantation, (X5) bone graft, (X6) implant diameter, (X8) I-stage/II-stage implantation, and (X9) insertion torque (Table 4). The relative weight coefficients (presented as standardized coefficients) of these factors were as follows: (X1) 0.111, (X3) 0.121, (X4) 0.148, (X5) −0.235, (X6) 0.119, (X8) 0.241, and (X9) 0.286. The equation used to calculate the ISQ values with the contribution of each factor is as follows:

(1)

Table 4 Multivariate linear regression analysis to analyze the weight coefficient of each influencing factor for the values of implant stability quotient that were measured immediately after implantation T1 Note: X1, sex; X3, maxillary/mandibular location; X4, immediate/delayed implantation; X5, the need of bone grafting; X6, implant diameter; X8, I/II-stage implantation; X9, insertion torque. Abbreviations: unstand coef, unstandardized coefficients; stand coef, standardized coefficients; SE, standard error.

At T2, the ISQ values were significantly influenced by three factors: (X6) implant diameter, (X9) insertion torque, and (X11) T1–T2 time interval (Table 5). The equation used to calculate the ISQ value with the contribution of each factor is as follows:

(2)

Table 5 Multivariate linear regression analysis to analyze the weight coefficient of each influencing factor for the values of implant stability quotient that were measured right before loading T2 Note: X6, implant diameter; X9, insertion torque; X11, T1–T2 time interval. Abbreviations: unstand coef, unstandardized coefficients; stand coef, standardized coefficients; SE, standard error.

The relative weight coefficients of these factors were as follows: (X6) 0.414, (X9) 0.150, and (X11) 0.191.

Discussion

In the field of dental implantology, a consensus has been reached that sufficient primary stability is critical in order to provide a mechanically stable microenvironment for the proper establishment of implant osseointegration – the biological basis for the secondary stability and for full implant functionality. Consequently, the availability of numeric stability values is a prerequisite for the estimation of the loading time schedule and the assessment of the long-term success rate of implants. RFA is a tool for the rapid, easy, objective and noninvasive measurements of the stability of implants without causing any patient discomfort. In a recent well-controlled in vitro study, ISQ values measured with RFA were found to be proportional to the mechanical stability of implants.¹⁹ On this basis, ISQ values are widely used as a basic parameter for clinical decision making. A precise and reliable estimation of the ISQ value in each case is thus a fundamental need to provide grounding for designing a realistic and accurate treatment plan. In this study, using a retrospective analysis, the possible role of eleven different candidate factors was considered. On these grounds, we formulated a mathematical model to estimate the weight coefficients of candidate factors for a more precise assessment of both the primary and secondary implant stabilities (Tables 4 and 5).

The design of an implant is one of the most fundamental elements to affect the implant primary and secondary stability.⁹ The design features consist of two major categories: 1) the macrodesign, such as thread design and body shape and 2) the microdesign, such as the implant topography.⁹ Gehrke et al recently indicated that the conical implants with a wide pitch were associated with significantly greater primary stability values than the semiconical implants with narrow pitch bores. In our study, we used only one implant type (SICace) with an identical macro- and microdesign, which thus may exclude the potential influence of implant design factors. Therefore, we did not include the implant design as a candidate factor in our analysis. Similarly, the preparation technique of the surgical site may also potentially influence implant stability.²⁷ This parameter was also excluded in this study, since the surgical site preparation was performed by the same experienced implantologist using one single implant system.

Bone type was not found to be a determining parameter influencing either T1 or T2 in our study. This finding was consistent with a recent 1-year follow-up study with 101 implants.²⁸ In that study, it was concluded that the baseline microstructural bone characteristics that were assessed by histomorphometric and microtomographic analyses did not significantly influence implant stability. Furthermore, using a similar classification method as in this study, the bone type was found not to be a significant influencing parameter either.²⁹

Apart from the implant design, the diameter and length of implants were other implant-related factors that might influence implant stabilities. In a recent in vitro biomechanical study, the primary stability of wider implants was found to be significantly higher in hard bone than the narrower implants using insertion torque as a parameter.²³ However, such differences have not been confirmed when using ISQ values as the estimator. These conflicting data might originate from a much smaller correlation (than generally assumed) between micromotion and insertion torque values than those obtained with ISQ measurements.¹⁹ In fact, in a small-scale prospective clinical trial, Han et al¹³ showed that ISQ values were not correlated with implant diameter values over a 12-week postoperative monitoring time period. However, in our retrospective study with 329 implants, the implant diameter was found to be a significant parameter influencing ISQ values both at T1 (Table 4) and T2 (Table 5). At T1, using equation 1, the 1.5 mm diameter difference between the 3.5 mm and 5 mm implants could be transformed into a difference of 2.503±1.131 (calculated by multiplying 1.5 by 1.669) in ISQ values. However, its weight coefficient was 0.119, which was quite similar with X1, X3, and X4, but much lower than X5, X8, and X9. These data suggested that the implant diameter was a significant but relatively mild influencing factor to estimate ISQ values at T1. In contrast, such 1.5 mm difference in implant diameter could be transformed into a difference of 6.120±1.047 at T2. The weight coefficient of implant diameter (0.414) was also much higher than X9 (0.150) and X11 (0.191) at this time point. These results thus indicated that the implant diameter was a major influencing factor on ISQ values at T2 (Table 5). Previous studies also showed that implant diameters could significantly influence ISQ values.^30,31 In contrast to this, the implant length was not found to be a significant influencing parameter at either T1 or T2 time points in our study. This finding was consistent with a previous study showing that implant length did not significantly influence primary stabilities of implants.²⁹ However, the implant length still might play a role in influencing implant stability provided that singly calculated correlations between implant length and implant stabilities were performed.^32,33 Furthermore, in particular cases, such as in patients with low bone quality, the optimization of the implant length and diameter should be considered in order to achieve higher primary implant stability values.³⁴

The maxillary/mandibular location was expected to represent a determining parameter influencing ISQ values, and indeed most implants in the maxilla had an ISQ of <60, and those in the mandible had an ISQ of >60.³⁵ It was also found that the ISQ values were generally higher in the mandible (59.8) than in the maxilla (55.0), but when using cylindrical implants, then they were not associated with a significant difference.²⁹ Furthermore, a similar phenomenon was also observed by Gehrke and Neto.³⁰ In contrast to this, mandibular implants were found to show statistically higher ISQ values than maxillary implants.³¹ In our study, we showed that the maxillary/mandible implant location was clearly a significant influencing factor at T1, but not at T2. According to the equation 1, the mandibular location might confer implants with 1.471±0.652 (mean ± standard error [SE]) higher values than those of the maxillary location. The weight coefficient of this factor was 0.121, which indicated its mild influence. This finding may also explain why a significant difference was not always detectable, even though a higher value was always found in the mandibular implants.

Immediate implantation is able to significantly shorten the clinical treatment time. Therefore, immediate implantation has been extensively evaluated (provided favorable conditions are given) in the last 2 decades, and it has been reported to yield success rates ranging from 92.7% to 98%.³⁶ The 7-year cumulative survival rate for immediately placed implants with an immediate loading scheme could also reach 94.6% success rate.³⁷ In a long-term follow-up study, no significant differences in the success rates and in the esthetic outcomes between immediately and delayed placed implants¹⁷ were reported. Gehrke et al²⁰ recently showed that delayed placed implants bore insignificantly higher ISQ values than the immediately placed implants. In our study, we showed that immediate/delayed implantation was a significant influencing factor on ISQ values at T1, at which a delayed implantation might confer implants with 1.836±0.664 (mean ± SE) higher ISQ values than immediate implants do (Table 4). However, at T2, this parameter is not significantly different anymore between the two groups (Table 5). These data from multivariate linear regression analyses were consistent with those from paired t-test (Table 3). These findings showed that, with a careful selection of cases, an immediate implantation exhibited no significant difference in secondary stabilities when comparing with delayed implantation. However, immediate/delayed implantation can result in significantly different ISQ values when considering maxillary locations.³⁸

Similarly, for some other candidate factors, conflicting findings were found regarding the relationship between sex and ISQ values. Previous studies showed that males were associated with either significantly higher,³⁹ or significantly lower⁴⁰ or similar⁴¹ ISQ values when comparisons were done with females. Guler et al⁴² showed that the sex parameter indeed influenced the ISQ values significantly only if a second measurement was done. This inconsistency may be due to a large variation of the experimental conditions, such as the choice of the measurement time point, special implant locations and inclusion of different types of populations/ethnic groups. In our study, the female patients showed 1.317±0.622 (mean ± SE) higher ISQ values than the males (which was a significant difference at T1, but not at T2). We did not identify a significant influence of the age of the patient on the ISQ values at either T1 or T2.

In our study, the need of bone grafting indeed negatively influenced ISQ values. A 4.990±0.622 (mean ± SE) lower ISQ value could be expected when there was such a need. This sounded reasonable since such a need was indeed associated with significantly smaller bone coverage of the implants. The II-stage healing pattern showed significantly higher ISQ values (2.961±0.622 [mean ± SE]) than the I-stage healing pattern at T1. This was also not unexpected since the II-stage healing pattern was performed with insertion torques <20 N or the ISQ value <65 in this study. At T2, this factor became insignificant, which suggested that I/II-stage implantation might not influence the osseointegration process. Consistently, I/II-stage implantation was previously shown not to result in different degrees of osseointegration.⁴³

One limitation of this study is that the equations might be specific for the implantologist, this implant system and/or this dental clinic. Careful interpretation is thus needed if extrapolation of the current data is planned to estimate ISQ values for patients/implants of other implantologists. However, with this study, we would like to provide a mathematical basis to analyze the weight coefficients of potential influencing factors. Every implantologist can establish his or her own equation to more precisely estimate ISQ values for the future cases. In future studies, we will further investigate the reliability and accuracy of this mathematical model for other types of implants.

Conclusion

Among the eleven candidate parameters, seven key factors influencing the ISQ values at T1 were identified, and only three key factors at T2. Within the limitations of this study, the mathematical model used enabled us to evaluate not only the significance but also the weight coefficients of various influencing parameters, which thus provides a viable novel method to more accurately estimate the ISQ values of implants.

Acknowledgments

This study was supported by the funds of China Scholarship Council, National Natural Science Foundation of China (grant nos 81400475 and 81470724), and Zhejiang Provincial Natural Science Foundation of China (grant no LY13H140006).

Disclosure

The authors report no conflicts of interest in this work.

---

References

1.		Branemark PI. Osseointegration and its experimental background. J Prosthet Dent. 1983;50:399–410.
2.		Guo CY, Matinlinna JP, Tang AT. Effects of surface charges on dental implants: past, present, and future. Int J Biomater. 2012;2012:381535.
3.		Dottore AM, Kawakami PY, Bechara K, et al. Stability of implants placed in augmented posterior mandible after alveolar osteotomy using resorbable nonceramic hydroxyapatite or intraoral autogenous bone: 12-month follow-up. Clin Implant Dent Relat Res. 2014;16(3):330–336.
4.		Caulier H, Naert I, Kalk W, Jansen JA. The relationship of some histologic parameters, radiographic evaluations, and Periotest measurements of oral implants: an experimental animal study. Int J Oral Maxillofac Implants. 1997;12(3):380–386.
5.		Teerlinck J, Quirynen M, Darius P, van Steenberghe D. Periotest: an objective clinical diagnosis of bone apposition toward implants. Int J Oral Maxillofac Implants. 1991;6(1):55–61.
6.		Derhami K, Wolfaardt JF, Faulkner G, Grace M. Assessment of the periotest device in baseline mobility measurements of craniofacial implants. Int J Oral Maxillofac Implants. 1995;10(2):221–229.
7.		Huang HM, Chiu CL, Yeh CY, Lin CT, Lin LH, Lee SY. Early detection of implant healing process using resonance frequency analysis. Clin Oral Implants Res. 2003;14(4):437–443.
8.		Meredith N, Alleyne D, Cawley P. Quantitative determination of the stability of the implant-tissue interface using resonance frequency analysis. Clin Oral Implants Res. 1996;7(3):261–267.
9.		Gehrke SA, Neto UTD, Del Fabbro M. Does implant design affect implant primary stability? A resonance frequency analysis-based randomized split-mouth clinical trial. J Oral Implantol. 2015;41(6):E281–E286.
10.		Meredith N. Assessment of implant stability as a prognostic determinant. Int J Prosthodont. 1998;11(5):491–501.
11.		Al-Jetaily S, Al-Dosari AA. Assessment of Osstell and Periotest(R) systems in measuring dental implant stability (in vitro study). Saudi Dent J. 2011;23:17–21.
12.		Lozano-Carrascal N, Salomó-Coll O, Gilabert-Cerdà M, Farré-Pagés N, Gargallo-Albiol J, Hernández-Alfaro F. Effect of implant macro-design on primary stability: a prospective clinical study. Med Oral Patol Oral Cir Bucal. 2016;21(2):e214–e221.
13.		Han J, Lulic M, Lang NP. Factors influencing resonance frequency analysis assessed by Osstell mentor during implant tissue integration: II. Implant surface modifications and implant diameter. Clin Oral Implants Res. 2010;21(6):605–611.
14.		Huwiler MA, Pjetursson BE, Bosshardt DD, Salvi GE, Lang NP. Resonance frequency analysis in relation to jawbone characteristics and during early healing of implant installation. Clin Oral Implants Res. 2007;18(3):275–280.
15.		Sim CP, Lang NP. Factors influencing resonance frequency analysis assessed by Osstell mentor during implant tissue integration: I. Instrument positioning, bone structure, implant length. Clin Oral Implants Res. 2010;21(6):598–604.
16.		Sennerby L, Meredith N. Resonance frequency analysis: measuring implant stability and osseointegration. Compend Contin Educ Dent. 1998;19(5):493–498,500,502. [quiz 504].
17.		Mangano FG, Mangano C, Ricci M, Sammons RL, Shibli JA, Piattelli A. Esthetic evaluation of single-tooth Morse taper connection implants placed in fresh extraction sockets or healed sites. J Oral Implantol. 2013;39(2):172–181.
18.		Koh RU, Rudek I, Wang HL. Immediate implant placement: positives and negatives. Implant Dent. 2010;19(2):98–108.
19.		Brizuela-Velasco A, Alvarez-Arenal A, Gil-Mur FJ, et al. Relationship between insertion torque and resonance frequency measurements, performed by resonance frequency analysis, in micromobility of dental implants: an in vitro study. Implant Dent. 2015;24(5):607–611.
20.		Gehrke SA, da Silva Neto UT, Rossetti PH, Watinaga SE, Giro G, Shibli JA. Stability of implants placed in fresh sockets versus healed alveolar sites: early findings. Clin Oral Implants Res. 2016;27(5):577–582.
21.		Gehrke SA, Guirado JL, Bettach R, et al. Evaluation of the insertion torque, implant stability quotient and drilled hole quality for different drill design: an in vitro Investigation. Clin Oral Implants Res. Epub 2016 Mar 8.
22.		Deli G, Petrone V, De Risi V, Tadic D, Zafiropoulos GG. Longitudinal implant stability measurements based on resonance frequency analysis after placement in healed or regenerated bone. J Oral Implantol. 2014;40(4):438–447.
23.		Romanos GE, Delgado-Ruiz RA, Sacks D, Calvo-Guirado JL. Influence of the implant diameter and bone quality on the primary stability of porous tantalum trabecular metal dental implants: an in vitro biomechanical study. Clin Oral Implants Res. Epub 2016 Feb 24.
24.		Wentaschek S, Scheller H, Schmidtmann I, et al. Sensitivity and specificity of stability criteria for immediately loaded splinted maxillary implants. Clin Implant Dent Relat Res. 2015;17(suppl 2):e542–e549.
25.		Rinaldi M, Ganz SD, Mottola A. Computer-Guided Applications for Dental Implants, Bone Grafting, and Reconstructive Surgery (adapted translation). China: Elsevier; 2015.
26.		Lekholm U, Zarb GA. Patient selection and preparation. In: Branemark P-I, Zarb GA, Albrektsson T, editors. Tissue Integrated Prostheses: Osseointegration in Clinical Dentistry. Chicago: Quintessence; 1985:199–209.
27.		Rastelli C, Falisi G, Gatto R, et al. Implant stability in different techniques of surgical sites preparation: an in vitro study. Oral Implantol. 2014;7(2):33–39.
28.		Dias DR, Leles CR, Lindh C, Ribeiro-Rotta RF. Marginal bone level changes and implant stability after loading are not influenced by baseline microstructural bone characteristics: 1-year follow-up. Clin Oral Implants Res. Epub 2015 Dec 9:1–9.
29.		Bischof M, Nedir R, Szmukler-Moncler S, Bernard JP, Samson J. Implant stability measurement of delayed and immediately loaded implants during healing. Clin Oral Implants Res. 2004;15(5):529–539.
30.		Gehrke SA, Neto UTD. Does the time of osseointegration in the maxilla and mandible differ? J Craniofac Surg. 2014;25(6):2117–2120.
31.		Liaje A, Ozkan YK, Ozkan Y, Vanlioglu B. Stability and marginal bone loss with three types of early loaded implants during the first year after loading. Int J Oral Maxillofac Implants. 2012;27(1):162–172.
32.		Tsolaki IN, Najafi B, Tonsekar PP, Drew HJ, Sullivan AJ, Petrov SD. Comparison of osteotome and conventional drilling techniques for primary implant stability: an in vitro study. J Oral Implantol. Epub 2016 Mar 3.
33.		Tozum TF, Turkyilmaz I, Bal BT. Initial stability of two dental implant systems: influence of buccolingual width and probe orientation on resonance frequency measurements. Clin Implant Dent Relat Res. 2010;12(3):194–201.
34.		Barikani H, Rashtak S, Akbari S, Badri S, Daneshparvar N, Rokn A. The effect of implant length and diameter on the primary stability in different bone types. J Dent (Tehran). 2013;10(5):449–455.
35.		Nedir R, Bischof M, Szmukler-Moncler S, Bernard JP, Samson J. Predicting osseointegration by means of implant primary stability. Clin Oral Implants Res. 2004;15(5):520–528.
36.		Penarrocha M, Uribe R, Balaguer J. Immediate implants after extraction. A review of the current situation. Med Oral. 2004;9:234–242.
37.		Barone A, Marconcini S, Giammarinaro E, Mijiritsky E, Gelpi F, Covani U. Clinical outcomes of implants placed in extraction sockets and immediately restored: a 7-year single-cohort prospective study. Clin Implant Dent Relat Res. Epub 2016 Feb 16.
38.		Granic M, Katanec D, Vucicevic Boras V, et al. Implant stability comparison of immediate and delayed maxillary implant placement by use of resonance frequency analysis – a clinical study. Acta Clin Croat. 2015;54:3–8.
39.		Zix J, Kessler-Liechti G, Mericske-Stern R. Stability measurements of 1-stage implants in the maxilla by means of resonance frequency analysis: a pilot study. Int J Oral Maxillofac Implants. 2005;20(5):747–752.
40.		Brochu JF, Anderson JD, Zarb GA. The influence of early loading on bony crest height and stability: a pilot study. Int J Prosthodont. 2005;18(6):506–512.
41.		Ostman PO, Hellman M, Wendelhag I, Sennerby L. Resonance frequency analysis measurements of implants at placement surgery. Int J Prosthodont. 2006;19(1):77–83. [discussion 84].
42.		Guler AU, Sumer M, Duran I, Sandikci EO, Telcioglu NT. Resonance frequency analysis of 208 Straumann dental implants during the healing period. J Oral Implantol. 2013;39(2):161–167.
43.		Degidi M, Daprile G, Piattelli A. Primary stability determination of implants inserted in sinus augmented sites: 1-step versus 2-step procedure. Implant Dent. 2013;22(5):530–533.