Modeling the economic outcomes of immuno-oncology drugs: alternative model frameworks to capture clinical outcomes

Introduction

Reliable evidence to determine long-term cost-effectiveness is frequently absent when a marketing authorization application is submitted for a new therapy. This evidence is central to recent debates around the affordability of cancer drugs and the sustainability of high drug prices.^1–3 The tension between effective management of health care budgets and the provision of optimal care to cancer patients highlights the need for decision makers to assess the true value of cancer treatments using the most rigorous and robust methods.^4,5

Together with the challenge of affordability, an accurate depiction of the true impact of anticancer medication is critical particularly given escalating price benchmarks accompanied by, in some cases, only moderate improvements in overall survival (OS). Comparing treatment effect can be complex; this is particularly true given the numerous surrogate endpoints often used in clinical trials which may, or may not, be predictive of a true OS benefit.^1,6 In the evaluation of new treatments, a balance between disease progression and treatment-related toxicities is key to determining clinically meaningful outcomes for patients. To improve cross product and disease area comparisons, the European Society for Medical Oncology (ESMO) has developed a reproducible tool which can be applied to new anticancer treatments to assess the magnitude of clinical benefit (ESMO Magnitude of Clinical Benefit Scale). The tool grades each trial within the curative and non-curative disease settings using a two-part rule. Firstly, the lower limit of the 95% confidence interval (CI) on the hazard ratio is compared with specified thresholds. Secondly, the observed absolute difference in treatment outcomes is compared with the minimum absolute gain considered as beneficial.^7,8

As more innovative treatments are introduced, the value defined by conventional economic modeling requires renewed scrutiny given the complex technical and data availability issues raised by new therapies.^4,5

An established approach to economic modeling in oncology is the three-state partitioned survival model (PSM), which classifies patients into the states of “progression free,” “progressive disease” (PD), and “death” (Figure 1). The approach mirrors the data on progression-free survival (PFS) and OS commonly reported in clinical trials, and is designed to evaluate therapies in which the course of disease is relatively easily captured by a limited number of health states.⁹

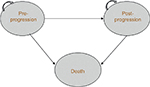Figure 1 Three-state partitioned survival model. Patients can remain in pre- or post-progression, move from pre- to post-progression, or move from either state to death.

Particular challenges for economic modeling in oncology have been raised by the emergence of checkpoint inhibitors, which are a new therapeutic class of immuno-oncology (I-O) compounds,¹⁰ an evolving treatment modality that harnesses the immune system to fight cancer. Fundamental differences in pharmacodynamic and anticancer properties of I-O compared with conventional therapies call for innovative ways to model patient response to treatment. In particular, treatment response with I-O drugs differs from progression with conventional therapies, an example being “pseudo-progression” (ie, tumor growth from treatment effect rather than true disease progression) that has been described with immune checkpoint inhibitors in melanoma. One may inaccurately assess these unique I-O-associated clinical response parameters which, in turn, may prevent robust cost-effectiveness analysis and value-based assessments^11,12 – as demonstrated in the survival extrapolation of I-O with traditional data fits versus more flexible approaches.¹³

While conventional therapies demonstrate early benefit but often with limited durability (Figure 2A, B),^11,14 some patients treated with I-O therapy tend to exhibit delayed response, followed by subsequent long-term survival.¹⁵ This typically occurs in about 20%–30% of patients across several tumor sites.^16–18 Meanwhile, the potential for quality of life to be maintained in melanoma has been demonstrated with nivolumab.¹⁹

Figure 2 Kaplan–Meier plots for (A) PFS for both treatment arms, (B) OS for both treatment arms, and data fits of conventional and flexible methods applied to (C) PFS for nivolumab, (D) PFS for dacarbazine, (E) OS for nivolumab, and (F) OS for dacarbazine. Abbreviations: RCS, restricted cubic splines; CI, confidence interval; PFS, progression-free survival; OS, overall survival.

Related to the differences in clinical response is the duration of therapy needed to sustain such responses. Traditionally, a treat to progression approach has been used, but there is emerging evidence that a shorter duration of therapy can still be associated with sustained clinical response. In addition, clinical trials in some indications have revealed treatment beyond progression (where treatment is still tolerated) as response continues to be seen irrespective of the standard definition of progression. This highlights the need for models to capture time on treatment as well as disease progression.

Improvements on existing model frameworks used in cost-effectiveness analyses could include increasing the number of health states in the traditional model, partitioning of data based on patient prognosis or clinical outcomes, or patient-level approaches that account for greater heterogeneity. Such methods have the potential to demonstrate significant improvements over a three-state model without addressing the fundamental differences that the patterns of survival associated with I-O imply. To deal with some of these issues, other economic measures that may be applicable have been proposed (eg, assessing survival benefit over a daily scale).^1,3,6,8 A key issue is whether economic models can be designed to provide more clinically relevant representations of disease compared with the traditional approaches, which continue to be applied in published cost-effectiveness analyses.^20–22 A related challenge is the extent to which the data typically collected as part of clinical trials are reflective of disease dynamics in I-O therapies, potentially constraining analysts’ ability to develop more sophisticated approaches. By testing innovative economic model approaches, the aim of this paper is to explore new ways of aligning model structure with clinical observations in I-O therapy, and to contribute to the development of economic evaluation guidelines in this area.

Materials and methods

This paper presents an empirical application of a range of economic model structures varying in terms of numbers and definitions of health states. These health states are tested against a set of I-O data drawn from one randomized trial in malignant melanoma (CheckMate 066).¹² The models are used to investigate how increasingly refined structures, compared with the reference point of the traditional three-state PSM, can help provide more detailed evidence of value for decision making. While the approach is intended to be generalizable to other disease areas and therapeutic options, the picture of immune responses to different single and combination therapies is still emerging. To reinforce good practice and consistency in economic model development, an initial generalized approach to the selection of model frameworks is presented and the implications for economic evaluation in I-O are drawn out. The empirical application is then reported using a stepwise approach to develop models of increasing complexity within that framework.

Selection of model framework

A number of general methodological guidelines exist on decision analytic modeling for the economic evaluation of health care interventions.^23–25 Those which focus specifically on the structural design of models^26–28 identify patient heterogeneity as a critical factor in model selection. Where heterogeneity between groups is an issue, as is the case with I-O therapy, a well-known method of overcoming the homogeneity assumptions inherent in economic models is to increase the number of states in the model,²⁶ with the health states designed to represent the natural history of disease, treatments, and their effects.²⁷ In the context of I-O therapy, limiting the model to pre-progression (PP) and post-progression (PsP) health states is unlikely to capture adequately the evolution of the disease and patients’ response to treatment. This has been recognized to some extent in health technology assessments by the National Institute for Health and Care Excellence (NICE), with some submissions for example, extending the basic model by introducing an on treatment/off treatment distinction,^29,30 while others have retained the three-state model.^31,32

To make allowances for different patient attributes, health states can be subdivided depending on the impact on health outcomes of various risk factors, which might include stages of the natural history of disease.²⁷ Disadvantages of increasing the number of health states are an increase in model complexity,²⁸ with the potential for reduced transparency and ease of validation, and, in some cases, the placing of excessive demands on data availability. On the other hand, caution has been expressed about simplifying a complex model as it equates to adjusting one or more model parameters,²⁶ a step which may not be justified. In some situations, the identification of a clinically relevant set of health states which capture the important aspects of the condition under investigation may necessitate a reconsideration of the fundamental model structure. If a large number of health states are relevant (and can be supported by data), it is recommended that there is a need to consider individual level modeling.²⁷

More complex approaches, in terms of the number and types of health states defined, reduce the number of observations to populate each health state and stretch the ability of the available data to match the theoretical concepts embodied in those health states. This may not be excessively restrictive if data can be sourced from general scientific literature. In the current context of implementing different model structures on the basis of data from a single clinical trial, there is a trade-off between the number of health states and the number of patient observations with which to populate each individual health state. A potential conflict explored in this study (and one which could usefully be addressed in early economic modeling to inform clinical development programs) is between increased sophistication in the portrayal of the condition being investigated and an effective reduction in the available data, with a consequent increase in uncertainty in the model.

Empirical application

Patient population and trial data

The analysis of treatment outcomes was based on patient-level data from the CheckMate 066 (the clinical trial was funded by Bristol-Myers Squibb; ClinicalTrials.gov number NCT01721772) randomized Phase III clinical trial of nivolumab (N=210, 3 mg/kg every 2 weeks) versus dacarbazine (N=208, 1000 mg/m² body surface every 3 weeks) in treatment-naïve melanoma patients without the BRAF mutation (average age of 65 years). The primary endpoint of OS was reported alongside secondary endpoints of PFS and objective response rate (ORR). Patients were treated until progression, with tumor response assessed according to Response Evaluation Criteria in Solid Tumors (RECIST; version 1.1),³³ except those who had a clinical benefit without experiencing substantial adverse events. Following discontinuation, patients (30.0% in the nivolumab group and 54.8% in the dacarbazine group) received systemic treatment, most commonly ipilimumab, another checkpoint inhibitor that was approved by the US Food and Drug Administration for melanoma in 2011.¹⁷

At the first database lock (August 2014, 16.7 months), median OS had not been reached in the nivolumab group (ORR of 40%) and was 10.8 months (ORR of 13.9%) in the dacarbazine group. Median PFS and percentage survival at 1 year were significantly longer with nivolumab (5.1 months and 72.9%) compared with dacarbazine (2.2 months and 42.1%).^14,34 At the second database lock (July 2015), OS at 2 years showed a significantly higher proportion surviving in the nivolumab group (57.7%) compared with dacarbazine (26.7%).³⁵

Trial data available for the current analysis included up to 34 months’ follow-up (nivolumab) and 27 months (dacarbazine) for PFS and 36 months for OS (both arms). Crossover to ipilimumab was allowed from July 2014. Baseline characteristics, ORR, and disease status were available and extracted to supplement the model structures. Clinical outcomes generated by the model frameworks presented in this paper were compared with the trial results reported in Table 1.

Table 1 Overview of the results from the CheckMate 066 trial and comparisons to clinical outcomes from the conventional PSM, extended versions of the conventional PSM, and the immune-response-based Markov model* Note: *Patients treated with dacarbazine cannot access the I-O health states in models 2–4. **The differentiation between normal and I-O post-progression is provided in brackets. Abbreviations: CR, complete response; PR, partial response; NR, not reached; PD, progressive disease; SD, stable disease; PSM, partitioned survival model; I-O, immuno-oncology.

Model structures

To understand the value of different model frameworks, a stepwise approach to model development (based on clinical input) was taken. The health states considered were chosen to be clinically relevant to patients treated with I-O drugs. For the purposes of capturing the expected benefits of I-O therapy in delayed progression and prolonged survival (in the relevant subset of patients), and to provide a framework that is flexible enough to address some of the limitations of the conventional approach and I-O data (including immature OS and PFS data), three additional frameworks were developed. Two of the three were extensions of the conventional PSM approach, incorporating a broader set of health states but yielding the same estimates of survival. The other was a state-transition model designed to capture the impact of I-O therapy in terms of immune response (Figure 3A–D).

Figure 3 Model schematics for the (A) conventional three-state PSM, (B) conventional three-state PSM with the additional health state to differentiate levels of response, (C) conventional three-state PSM with additional health states to differentiate levels of response and progression types, (D) immune-response-based Markov model. Abbreviations: PSM, partitioned survival model; I-O, immuno-oncology.

As the additional health states in the three new models were intended to capture a specific immune response, the non I-O group was restricted to the progression-free, PD, and death health states and was excluded from entering the I-O states.

Model 1: PSM

The conventional PSM typically used in the evaluation of oncology treatments involves partitioning survival into states of interest, and was used as a baseline against which to compare the other model frameworks. Model 1 is the standard three-state model including states of PP, PsP, and death (Figure 3A). Trial outcomes for PFS and OS were each modeled directly using survival analysis to allow for extrapolation. This approach did not consider PsP survival directly; instead, time to progression was derived from the difference between the areas under the PFS and OS curves.

Model 2: PSM extension with response differentiation

With the conventional approach, the PP state includes treatment responders and nonresponders. To provide a more definitive representation of response to treatment (and its duration), PP was segregated into PP without response (PP₁) and PP with response (PP₂). PP₁ defined patients with stable disease (SD) without clinical change in lesions, and PP₂ referred to patients with partial response (PR) or complete response (CR) to treatment, consistent with the trial definitions. The other health state definitions for PsP and death remain unchanged from the conventional approach (model 1). Based on the best overall response (BOR), the proportion responding (PR/CR) was applied to PFS to define the responder category. Similarly, the proportion with SD based on BOR was applied to PFS to define nonresponders. BOR is a standard approach to classify response categories although others are possible (eg, landmark models).

Trial outcomes for PFS (SD, CR, and PR) and OS were each modeled directly using survival analysis to allow for extrapolation. In line with model 1 (the conventional approach), progression was represented by the difference in the areas under the PFS (SD, and CR/PR) and OS curves.

Model 3: PSM extension with response and progression differentiation

The second extension (model 3, Figure 3C) classified post- progression into normal (PsP₁) and I-O progression (PsP₂) states, to reflect the differences in the underlying mechanism of action of treatment, which has given rise to the immune-related response criteria³⁶ alongside the RECIST³³ classification system. The health state definitions for PP were consistent with model 2.

In line with models 1 and 2, progression was represented by the difference in the areas under the PFS (SD, CR, and PR) and OS curves. A further adjustment was made to address the difference in progression types by applying the proportions who respond using BOR as an indicator (PsP₁) and who are nonresponders (PsP₂) to overall progression as reported in the CheckMate 066 trial.

Model 4: immune-response Markov state-transition model

A state-transition Markov model was developed to model the I-O mechanism in a more exhaustive way than was possible with the basic PSM and variants thereof. Patients in the model were allowed to move between states based on a set of transition probabilities estimated from reported clinical trial events defined by BOR. The model included states of treated/PP, no immune response (NIR), initial immune response (IIR), durable immune response (DIR), post-response progression (PRP), and death. The model can be applied to I-O treated patients and patients treated with other forms of therapy (chemotherapy or targeted therapy) although patients not treated with I-O are theoretically restricted to PP and NIR states. PP, NIR, IIR, DIR, and PRP states were mapped to available clinical trial data according to the following definitions:

• Treated/PP: nonfatal event of SD without progression
• NIR: nonfatal event of PD
• IIR: nonfatal event of PR without progression
• DIR: nonfatal event of CR without progression
• PRP: SD in responders with PR/CR

Transitions from 1) treated/PP to NIR, IIR, DIR, and death, 2) IIR to DIR, PRP, and death, 3) DIR to PRP and death, and 4) PRP to death were possible. Due to data limitations, all transition probabilities presented in Table 2 were based on the average patient experience over the period for which trial observations were available, rather than being estimated separately at each time point. Extrapolation beyond the period of data observation assumed time-invariant transition probabilities adjusted for the background mortality consistent with OS applied to PSM.

Table 2 Monthly transition probabilities adjusted for the immune-based Markov model (model 4) based on event rates from patient-level trial data from the CheckMate 066 trial for nivolumab and dacarbazine treatment arms Note: *Patients treated with dacarbazine cannot access the I-O health states in model 4. Abbreviations: CR, complete response; DIR, durable immune response; IIR, initial immune response; NIR, no immune response; PD, progressive disease; PP, pre-progression; PR, partial response; PRP, post-response progression; SD, stable disease; I-O, immuno-oncology.

Model estimation and outcomes

All models were constructed in Microsoft Excel 2010, using a lifetime time horizon, monthly cycles, and a half-cycle correction. Life years (LYs) and quality adjusted life years (QALYs) were discounted at 3.5% to represent the UK perspective for all model approaches. Clinical outcomes of OS, PFS, ORR, and BOR were compared with trial outcomes. Costs were excluded from the current analysis to focus on the way in which the different approaches modeled treatment outcomes.

Survival estimation

The process of fitting parametric survival curves to patient-level data was based on the NICE Decision Support Unit guidance,³⁷ with some modifications to handle I-O data.

For internal validation (prior to interpolation) and in the absence of long-term I-O data, the trial data were randomly partitioned into two datasets: 1) the “training” dataset used to assess the initial data fits and 2) the “validation” dataset used to confirm consistency for optimal model selection. Heterogeneity between the two datasets was assessed by comparing patient characteristics, Kaplan–Meier (K-M) plots, and primary outcomes with the core dataset, and applying a 95% CI to assess variance.¹³

Traditional parametric methods for Weibull, exponential, lognormal, and log-logistic functions, as well as flexible parametric survival models using restricted cubic splines (RCS) with 1–7 knots were fitted to both OS and PFS in each treatment arm. To assess the goodness of fit to the observed data for each predicted survival model, visual inspection against the K-M plots (for the overall fit and at the distinct I-O phases with emphasis on the plateau) was undertaken (Figure 2C–F). In addition, the Akaike information criterion and Bayesian information criterion statistical tests were compared among models and hazard plots examined.¹³

For OS, the lognormal function was used while, for PFS, the RCS with two knots was found to provide the best fit. The limited number of knots provides mitigation against overfitting the data although other approaches to validation, such as bootstrap resampling and k-fold cross-validation, are available. In the absence of long-term external data for nivolumab, ipilimumab studies with 5- and 10-year survival data were used to validate extrapolated survival estimates.^12,15,17 On the extrapolated portions of the OS and PFS curves, it was found that modeled PFS and OS crossed (which cannot happen in reality). As modeled PFS was based on a more mature dataset and better validated, it was taken to represent OS and PFS following the overlap of the two curves, an assumption considered to be conservative. Alternative methods of applying an adjustment factor to OS relative to PFS to capture additional survival benefit and surrogacy assumptions over OS in previous submissions have been explored in the evidence submitted to NICE³⁸ but rejected by the Evidence Review Group. In general, when extrapolating OS based on PFS, the background mortality should be accounted for to avoid potential overestimation.

Utility estimates

Health-related quality of life estimates suitable for calculating QALYs (utilities) were drawn from the literature and assigned to model health states, without differentiation between patients on and off treatment or between treatment arms. In the absence of literature for specific health states defined in the models presented, proxies based on closely related health states were used to estimate QALYs (Table 3).

Table 3 Utilities per health state per model39,40 and economic outcomes per model for 10 years, 20 years, and lifetime horizons Notes: *The same utility values apply to both treatment arms. The bold entries represent total outcomes ie, the sum of pre-progression, post-progression and death. Abbreviations: CR, complete response; LY, life years; PD, progressive disease; PR, partial response; QALY, quality adjusted life years; SD, stable disease; I-O, immuno-oncology.

For model 1, the utility values for the PP (0.802) and PsP (0.728) health states were drawn from a UK prospective study of individual patient-level data (the CheckMate 066 trial), adjusted for significant predictors of utility over time (baseline utility, progression status, time to death or end of follow-up, and treatment arm).³⁹

For models 2–4, the analysis used estimates from a universal set of utility values relating to clinical response states for PR, SD, and PD in advanced melanoma for the general UK population, to capture the variation in utilities with treatment response.⁴⁰ The utility estimate for SD (0.770)⁴⁰ was allocated to the PP₁ health states in models 2 and 3, and to the treated/PP health state in model 4. The PR (0.850)⁴⁰ utility value was assigned to the PP₂ state in models 2 and 3, and to the IIR and DIR states in model 4 (in the absence of information to differentiate between the level of response). The PD (0.590)⁴⁰ estimate was assigned to PsP in model 2, to PsP₁ and PsP₂ states in model 3, and to NIR and PRP states in model 4 (in the absence of information to differentiate between progression in responders and nonresponders).

Compliance with ethical standards

The protocol and amendments for the CheckMate 066 trial were reviewed by the institutional review board at each trial site. The study’s Independent Data Monitoring Committee (DMC) was established to provide oversight on the safety and efficacy considerations and provide advice to the sponsor regarding actions the DMC deemed necessary for the continuing protection of subjects enrolled in the study. The trial was conducted in accordance with the provisions of the Declaration of Helsinki and with Good Clinical Practice guidelines as defined by the International Conference on Harmonisation. All the patients provided written informed consent before enrollment.

Results

Trial endpoints: PSM-based approaches

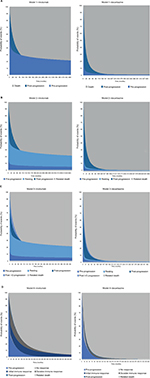
The modeling of OS benefit using the PSM frameworks over the trial period generated survival estimates of 73.3% (nivolumab) and 50.3% (dacarbazine) in year 1, and 58.7% (nivolumab) and 29.1% (dacarbazine) in year 2. These compared with reported trial outcomes in year 1 of 72.9% and 42.1% for nivolumab and dacarbazine, respectively, and in year 2 of 57.7% and 26.7%. The PSM-based approaches gave PFS of 40.5% (nivolumab) and 7.9% (dacarbazine) in year 1, with corresponding estimates of 35.8% and 5.2% in year 2 (Table 1). These findings were comparable with the trial reported PFS outcomes of 44.3% for nivolumab and 7.7% for dacarbazine in year 1, and 39.2% for nivolumab in year 2. Figure 4A–D provides model outcomes to illustrate event probabilities over a lifetime time horizon. With the partitioned approaches, nivolumab demonstrated long-term survival benefits in a subset of patients (21.2%), in contrast to dacarbazine, where survival beyond 15 years was minimal (≤1.0%).

Figure 4 Survival model plots for the (A) conventional PSM, (B) conventional PSM with additional health state to differentiate levels of response, (C) conventional PSM with additional health states to differentiate levels of response and progression types, (D) immune-response-based Markov model. Abbreviations: PSM, partitioned survival model; I-O, immuno-oncology.

Trial endpoints: immune-response Markov model

The Markov model’s OS estimates for nivolumab of 73.8% and 58.6% and for dacarbazine of 51.5% and 28.8% at years 1 and 2 were similar to those of the PSM-based approaches. In common with the PSM-based approaches, modeled OS in each year for nivolumab and in year 2 for dacarbazine were comparable with the trial results (Table 1). In contrast, modeled PFS estimates diverged markedly from those of the PSM approaches and from the trial results. While PFS estimates given by the model were 69.8% and 55.5% in years 1 and 2 for nivolumab and 48.6% in year 1 for dacarbazine, the corresponding trial results showed PFS of 44.3% and 39.2% for nivolumab, and 7.7% for dacarbazine. Whereas PFS estimates generated by models 1–3 were within 10% of the trial estimates, model 4 overestimated year 1 and year 2 PFS for nivolumab by nearly 60% and over 40%, respectively.

LYs and QALYs: PSM-based approaches

LY and QALY outcomes for each model are presented in Table 3. All the PSM-based approaches generated increasing increments in overall benefit (for nivolumab) with longer time horizons. The PSM frameworks (models 1–3) each gave the same overall LY outcomes, ranging from a gain in favor of nivolumab of 2.12 LYs over a 10-year time horizon to a gain of 5.13 LYs over a lifetime. Overall life expectancy for those receiving nivolumab was estimated at 3.9 years and 7.1 years for 10-year and lifetime time horizons, respectively. The incremental LY gains for nivolumab versus dacarbazine under the PSM approaches were reflective of the long-term survival of ~20% with nivolumab (Figure 4).

In model 1, the incremental QALY gain with nivolumab ranged from 1.68 QALYs to 3.99 QALYs as the time horizon increased from 10 years to the lifetime. Corresponding ranges for model 2 were 2.02–4.44 QALYs and, for model 3, 2.02–4.43 QALYs, thus doubling the gain by moving from the 10-year to a lifetime time horizon. Across the three models, overall quality adjusted life expectancy ranged between 2.83 and 3.01 QALYs under a 10-year time horizon and from 5.3 to 5.68 QALYs at a lifetime time horizon.

LYs and QALYs: immune-response Markov model

At a 10-year time horizon, estimates of life expectancy with nivolumab (3.78 LYs) under model 4 were comparable with the corresponding estimate in models 1–3 (3.9 LYs). However, at subsequent time horizons, life expectancy was estimated to be lower than in models 1–3, markedly so over the lifetime (5.35 vs 7.1 LYs). As life expectancy with dacarbazine did not differ substantially from that estimated in models 1–3 at any time horizon, the incremental LY gains with nivolumab were lower in model 4 (eg, 3.54 LYs over the lifetime compared with 5.13 LYs in models 1–3). QALYs showed a similar pattern, the incremental gain being estimated at 3.03 QALYs over the lifetime for nivolumab compared with 4.43 QALYs under model 3. Model 4 therefore provided a more conservative estimate of the long-term effect of nivolumab in comparison with models 1–3.

Assumptions and limitations

Interpretation of these findings should take into consideration a number of assumptions relied on by the Markov model which were not applicable to the PSM approaches. In particular, the transition probabilities on which the model is based were calculated as averages over the period for which BOR observations were available and assumed to be constant over this time period. Under the simpler formulation of health states, estimates of time progression-free or with progression are drawn directly from the OS and PFS curves. As a result, the Markov model may offer a set of health states which give a clinically more appropriate description of disease evolution and treatment response but, in this case, failed to represent the trajectory of progression as accurately as the simpler models.

The analysis reported here could be refined with longer follow-up and a closer alignment between the trial data and the concepts which the definitions of immune response are intended to capture. Alternatively, a multistate model with event history analysis which takes account of the timing of events could be used to estimate transition probabilities on a continuous time basis. This would overcome the limitations of the Markov model’s discrete time approach but presupposes access to patient-level data which may not always be available. In addition, the approach can be problematic given limited patient numbers.

Contrasting results from applying a PSM, Markov model, and a continuous time multistate model to a common dataset have been reported by Williams et al.⁴¹ Their example is not, however, directly comparable as some of the differences in QALY results reported here will be a result of the wider range of utilities facilitated by the more granular descriptions of health states. It should also be noted that the pros and cons of different approaches may depend on the precise therapeutic regimen investigated; further research is needed to explore the applicability of the models presented here in drugs with different mechanisms of action.

Discussion

Selection of health states

The three-state PSM distinguishing between PP, PsP, and death mirrors the outcomes of PFS and OS reported in clinical trials and is frequently used as the basis for estimating the cost-effectiveness of cancer therapies. Many researchers are contending with the issue of converting these data (to assess additional benefit of a new therapy to the existing therapies in place) into information which can be considered alongside the costs of new therapies (particularly drug prices) in health care decision making. Decisions about the use of new drugs are frequently based on the cost per QALY, although other ways of combining survival and quality of life have been proposed in the context of cancer treatment.^1,6 In the case of I-O therapy, all models have limitations given patient outcomes characterized by atypical patterns of survival and disease dynamics.

Observed patterns of response in I-O suggest that the conventional three-state model is likely to provide an unduly restrictive representation of the disease course and therapeutic mechanism of action. The issue has been addressed in this study by adding new health states intended to capture I-O treatment response, initially with two extensions to the basic PSM. The first introduces a new PP state while the second supplements this with a new PsP state. The final model defines a set of health states specifically targeted at concepts of immune response, with movements between states allowed according to a set of transition probabilities (Markov model).

Health states that are specific to I-O, namely immune response and post-immune progression, have clinical validity, and allow modeling of the “resting” patient with the potential for sustained benefit (improved survival and quality of life) and reduced costs. I-O-specific states can be accessed only through a transformative health state (immune response) which is not applicable to conventional therapies. An illustration is the evidence that treatment-free survival is possible with some patients who have received ipilimumab.¹⁵ The emergence of new evidence regarding responses to I-O therapy will influence the desired number and categorization of health states in the theoretical model to maintain clinical validity. In practice, there may be a trade-off between the value of the additional data they provide, and the degree of uncertainty introduced by data limitations or the assumptions required to support them.

The current study illustrates not only the gains but also the potential pitfalls in introducing increased sophistication into the model’s health states. The two extensions of the PSM provide a better overview of QALYs for those responding and not responding to treatment (giving increased QALY gains with I-O therapy due to the time spent in PP with response) and produced estimates of OS and PFS comparable with the basic PSM and trial data.

The developments represented by the Markov model are that it explicitly captures patients moving from one state to another in a way which is not possible with the PSM-based approaches, and that it provides further granularity of health state descriptions. However, the finding that its estimates of 1- and 2-year PFS were not in line with the PSM-based models and with the underlying data has revealed the limitations of the standard Markov approach which, in this case, was outperformed by the simpler variants of the PSM. Nevertheless, the Markov modeling approach has the potential to be more informative in the future with improvements in the understanding of I-O and in data sources. The implications for additional data collection and appropriate reporting if the potential for such models is to be fully exploited are worthy of further exploration.

Selection of model structure

Drawing on the literature cited²⁶ and discussion at a workshop of the Scientific Steering Committee (Vienna, October 2016) which oversaw this work, a high-level algorithm to guide the selection of the appropriate cost-effectiveness model structure when evaluating I-O therapy has been proposed (Figure 5).

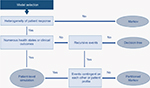Figure 5 Proposed model selection algorithm.

The selection of model structure should be based on a number of drivers of structural fit with the data. Population heterogeneity and predictability/heterogeneity of response to treatment (a factor particularly emphasized in Figure 5) need to be considered alongside complexity of the health states encountered (which will be greater in I-O than with other forms of therapy) and the contingency of events on prior patient events or treatment pathways.

In practice, the selection of the most appropriate model structure to estimate the cost-effectiveness of I-O therapies will tend, in most cases, to center on a choice between a patient-level simulation and a partitioned Markov in terms of goodness of structural fit. The level of complexity of the model will need to be informed not only by theoretical models of disease processes, in the same way that the choice of survival function when modeling PFS and OS will ideally benefit from a clinical understanding of disease processes, but also by empirical testing. As has previously been observed, the choice between a simpler and more complex model should depend on a consideration of both; a decision to opt for a simplified model “is an empirical issue, the answer to which is unknown without undertaking a more complex model.”²⁶

Ultimately, a model should be judged on its ability to mirror accurately the short- and long-term clinical outcomes observed in trials and real-world data sources. Choice of model should be informed both by the amount and value of the information generated to support appropriate decision making and by the level of uncertainty within the outputs. Sensitivity to assumptions can help to identify data that need to be collected (rather than influencing choice of structure).

Conclusion

Extending the standard three-state model to a four- or five-state structure (separating PP or both PP and PsP into two) can better reflect patients’ experience of disease during I-O therapy and potentially provide more transparent accounting of the source of treatment benefits. Going further to add specific I-O-relevant health states (independent of the underlying model framework) can be a useful tool to establish better coherence with clinical data and may deliver important information from a decision maker perspective. However, the compromises involved in implementing these states through a conventional Markov approach may result in a loss of accuracy in modeling the underlying data. Further research is needed to understand the appropriate number of disease states, underlying patient quality of life and resource use associated with those states, their validity across other tumor types, and the usefulness of other modeling approaches.

Acknowledgments

Bristol-Myers Squibb (BMS) funded the research. The authors are grateful to Clive Pritchard of Wickenstones Ltd for writing and editorial assistance.

Disclosure

A Juarez-Garcia, M Lees, AA Tahami Monfared, D Tyas, and Y Yuan were employed by BMS. N Begum, EJ Gibson, and I Koblbauer were employed by Wickenstones Ltd, who were funded by BMS to undertake the research. G Dranitsaris, D Liew, and P McEwan have received consultancy fees and have been reimbursed for travel expenses to attend advisory board meetings related to this research. The authors report no other conflicts of interest related to this work.

References

1.		Gozzo L, Navarria A, Drago V, et al. Linking the price of cancer drug treatments to their clinical value. Clin Drug Investig. 2016;36(7):579–589.
2.		Pfister DG. The just price of cancer drugs and the growing cost of cancer care: oncologists need to be part of the solution. J Clin Oncol. 2013;31(28):3487–3489.
3.		Experts in Chronic Myeloid Leukemia. The price of drugs for chronic myeloid leukemia (CML) is a reflection of the unsustainable prices of cancer drugs: from the perspective of a large group of CML experts. Blood. 2013;121(22):4439–4442.
4.		Miller JD, Foley KA, Russell MW. Current challenges in health economic modeling of cancer therapies: a research inquiry. Am Health Drug Benefits. 2014;7(3):153–162.
5.		Jönsson B, Wilking N. Cancer vaccines and immunotherapeutics: challenges for pricing, reimbursement and market access. Hum Vaccin Immunother. 2012;8(9):1360–1363.
6.		Guirgis HM. Proposal for a novel methodology to screen and score cost versus survival for anticancer drugs in metastatic disease: could cost weigh in evaluation? J Oncol Pract. 2012;8(4):224–230.
7.		Ellis LM, Bernstein DS, Voest EE, et al. American Society of Clinical Oncology perspective: raising the bar for clinical trials by defining clinically meaningful outcomes. J Clin Oncol. 2014;32(12):1277–1280.
8.		Cherny NI, Sullivan R, Dafni U, et al. A standardised, generic, validated approach to stratify the magnitude of clinical benefit that can be anticipated from anti-cancer therapies: the European Society for Medical Oncology Magnitude of Clinical Benefit Scale (ESMO-MCBS). Ann Oncol. 2015;26(8):1547–1573.
9.		Minacori R, Bonastre J, Lueza B, Marguet S, Levy P. How to model survival in cost-effectiveness analysis? Differences between Markov and partitioned survival analysis models. Value Health. 2015;18(7): A704.
10.		de Lorenzo F, Wait S, Karaca B, Britten C, van den Bulcke M; European Expert Group on Immuno-Oncology. Greater patient access to immuno-oncology therapies—what can policymakers do? Ecancermedicalscience. 2015;9:1–4.
11.		Chen T-T. Statistical issues and challenges in immuno-oncology. J Immunother Cancer. 2013;1:18.
12.		Schadendorf D, Hodi FS, Robert C, et al. Pooled analysis of long-term survival data from phase II and phase III trials of ipilimumab in unresectable or metastatic melanoma. J Clin Oncol. 2015;33(17):1889–1894.
13.		Gibson E, Koblbauer I, Begum N, et al. Modelling the survival outcomes of immuno-oncology drugs in economic evaluations: a systematic approach to data analysis and extrapolation. Pharmacoeconomics. 2017;35(12):1257–1270.
14.		Robert C, Long GV, Brady B, et al. Nivolumab in previously untreated melanoma without BRAF mutation. N Engl J Med. 2015;372(4):320–330.
15.		McDermott D, Lebbé C, Hodi FS, et al. Durable benefit and the potential for long-term survival with immunotherapy in advanced melanoma. Cancer Treat Rev. 2014;40(9):1056–1064.
16.		Borghaei H, Paz-Ares L, Horn L, et al. Nivolumab versus docetaxel in advanced nonsquamous non-small-cell lung cancer. N Engl J Med. 2015;373(17):1627–1639.
17.		Larkin J, Chiarion-Sileni V, Gonzalez R, et al. Combined nivolumab and ipilimumab or monotherapy in untreated melanoma. N Engl J Med. 2015;373(1):23–34.
18.		McDermott DF, Drake CG, Sznol M, et al. Survival, durable response, and long-term safety in patients with previously treated advanced renal cell carcinoma receiving nivolumab. J Clin Oncol. 2015;33(18):2013–2020.
19.		Long GV, Atkinson V, Ascierto PA, et al. Effect of nivolumab on health-related quality of life in patients with treatment-naïve advanced melanoma: results from the phase III CheckMate 066 study. Ann Oncol. 2016;27(10):1940–1946.
20.		Bohensky M, Pasupathi K, Gorelik A, Kim H, Harrison JP, Liew D. A cost effectiveness analysis of nivolumab compared to ipilimumab for the treatment of Braf wild-type advanced melanoma in Australia. Value Health. 2015;18(7):A340.
21.		Jensen IS, Zacherle E, Blanchette CM, Zhang J, Yin W. Evaluating cost benefits of combination therapies for advanced melanoma. Drugs Context. 2016;5:212297.
22.		Wang J, Chmielowski B, Pellissier J, Xu R, Stevinson K, Liu FX. Cost-effectiveness of pembrolizumab versus ipilimumab in ipilimumab-naive patients with advanced melanoma in the United States. J Manag Care Spec Pharm. 2017;23(2):184–194.
23.		Sculpher M, Fenwick E, Claxton K. Assessing quality in decision analytic cost-effectiveness models. A suggested framework and example of application. Pharmacoeconomics. 2000;17(5):461–477.
24.		Philips Z, Ginnelly L, Sculpher M, et al. Review of guidelines for good practice in decision-analytic modelling in health technology assessment. Health Technol Assess. 2004;8(36):iii–iv, ix–xi, 1–158.
25.		Caro JJ, Briggs AH, Siebert U, Kuntz KM. Modeling good research practices – overview: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force-1. Value Health. 2012;15(6):796–803.
26.		Barton P, Bryan S, Robinson S. Modelling in the economic evaluation of health care: selecting the appropriate approach. J Health Serv Res Policy. 2004;9(2):110–118.
27.		Brennan A, Chick SE, Davies R. A taxonomy of model structures for economic evaluation of health technologies. Health Econ. 2006;15(12):1295–1310.
28.		Briggs ADM, Wolstenholme J, Blakely T, Scarborough P. Choosing an epidemiological model structure for the economic evaluation of non-communicable disease public health interventions. Popul Health Metr. 2016;14:17.
29.		NICE. Single technology appraisal. Pomalidomide with dexamethasone for treating relapsed and refractory multiple myeloma after at least two regimens including lenalidomide and bortezomib (review of TA338) [ID985]; committee papers. London: National Institute for Health and Care Excellence; 2016. Available from: https://www.nice.org.uk/guidance/ta427/documents/committee-papers. Accessed September 24, 2017.
30.		NICE. Single technology appraisal. Nivolumab for treated or metastatic renal cell carcinoma. London: National Institute for Health and Care Excellence; 2016. Available from: https://www.nice.org.uk/guidance/ta417/documents/committee-papers-2. Accessed September 24, 2017.
31.		NICE. Committee papers single technology appraisal. Nivolumab for treating advanced (unresectable or metastatic) melanoma [ID845]. London: National Institute for Health and Care Excellence; 2016. Available from: https://www.nice.org.uk/guidance/ta417/documents/committee-papers-4. Accessed January 08, 2017.
32.		NICE. Single technology appraisal. Pembrolizumab for treatment of PD-L1 positive non-small cell lung cancer after platinum-based chemotherapy [ID840]. London: National Institute for Health and Care Excellence; 2016. Available from: https://www.nice.org.uk/guidance/ta428/documents/committee-papers. Accessed January 08, 2017.
33.		Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer. 2009;45(2):228–247.
34.		Asmar R, Yang J, Carvajal RD. Clinical utility of nivolumab in the treatment of advanced melanoma. Ther Clin Risk Manag. 2016;12:313–325.
35.		BMS. Opdivo (nivolumab): advanced melanoma (unresectable or metastatic). 2016. Available from: http://www.opdivo.co.uk/hcp/advanced-melanoma/first-line/progression-free-survival. Accessed November 23, 2016.
36.		Wolchok JD, Hoos A, O’Day S, et al. Guidelines for the evaluation of immune therapy activity in solid tumors: immune-related response criteria. Clin Cancer Res. 2009;15(23):7412–7420.
37.		Latimer N. NICE DSU Technical Support Document 14. Survival analysis for economic evaluations alongside clinical trials – extrapolation with patient-level data. Sheffield: University of Sheffield; 2013. Available from: http://nicedsu.org.uk/wp-content/uploads/2016/03/NICE-DSU-TSD-Survival-analysis.updated-March-2013.v2.pdf. Accessed March 23, 2017.
38.		NICE. Everolimus with exemestane for treating advanced breast cancer after endocrine therapy (Cancer Drugs Fund reconsideration of TA295). London: National Institute for Health and Care Excellence; 2016. Available from: https://www.nice.org.uk/guidance/ta421/resources/everolimus-with-exemestane-for-treating-advanced-breast-cancer-after-endocrine-therapy-pdf-82604658653125. Accessed December 08, 2017.
39.		Paly V, Colby C, Gilloteau I, Exuzides A, Briggs A. Predictors of utility over time among patients with treatment-naïve advanced melanoma from the phase 3 CheckMate 066 trial. Value Health. 2015;18(7):A474.
40.		Beusterien KM, Szabo SM, Kotapati S, et al. Societal preference values for advanced melanoma health states in the United Kingdom and Australia. Br J Cancer. 2009;101(3):387–389.
41.		Williams C, Lewsey JD, Mackay DF, Briggs AH. Estimation of survival probabilities for use in cost-effectiveness analyses: a comparison of a multi-state modeling survival analysis approach with partitioned survival and Markov decision-analytic modeling. Med Decis Making. 2017;37(4):427–439.