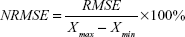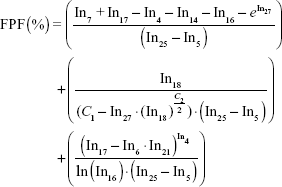Back to Journals » International Journal of Nanomedicine » Volume 10 » Issue 1
Empirical modeling of the fine particle fraction for carrier-based pulmonary delivery formulations
Authors Pacławski A, Szlęk J, Lau R, Jachowicz R, Mendyk A
Received 15 October 2014
Accepted for publication 13 November 2014
Published 21 January 2015 Volume 2015:10(1) Pages 801—810
DOI https://doi.org/10.2147/IJN.S75758
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 3
Editor who approved publication: Dr Thomas Webster
Video abstract presented by Adam Pacławski
Views: 733
Adam Pacławski,1 Jakub Szlęk,1 Raymond Lau,2 Renata Jachowicz,1 Aleksander Mendyk1
1Department of Pharmaceutical Technology and Biopharmaceutics, Jagiellonian University Medical College, Kraków, Poland; 2School of Chemical and Biomedical Engineering, College of Engineering, Nanyang Technological University, Singapore
Abstract: In vitro study of the deposition of drug particles is commonly used during development of formulations for pulmonary delivery. The assay is demanding, complex, and depends on: properties of the drug and carrier particles, including size, surface characteristics, and shape; interactions between the drug and carrier particles and assay conditions, including flow rate, type of inhaler, and impactor. The aerodynamic properties of an aerosol are measured in vitro using impactors and in most cases are presented as the fine particle fraction, which is a mass percentage of drug particles with an aerodynamic diameter below 5 µm. In the present study, a model in the form of a mathematical equation was developed for prediction of the fine particle fraction. The feature selection was performed using the R-environment package “fscaret”. The input vector was reduced from a total of 135 independent variables to 28. During the modeling stage, techniques like artificial neural networks, genetic programming, rule-based systems, and fuzzy logic systems were used. The 10-fold cross-validation technique was used to assess the generalization ability of the models created. The model obtained had good predictive ability, which was confirmed by a root-mean-square error and normalized root-mean-square error of 4.9 and 11%, respectively. Moreover, validation of the model using external experimental data was performed, and resulted in a root-mean-square error and normalized root-mean-square error of 3.8 and 8.6%, respectively.
Keywords: fine particle fraction, pulmonary delivery, deposition modeling, genetic programming, feature selection, empirical modeling
Introduction
Dry powder inhalers are frequently used in the treatment of a number of respiratory diseases, such as asthma and chronic obstructive pulmonary disease. The therapeutic efficiency of these drug formulations depends on the deposition of drug particles at different levels of the respiratory system. Aerodynamic diameter is usually applied for the description of particle behavior in the air stream and is determined by particle size, shape, and density. Small particles with an aerodynamic diameter of less than 5 μm are deposited deep in the lungs, but in most cases, they have poor flow properties as well as a highly cohesive nature, leading to low stability and poor quality of formulations.1,2 The addition of a carrier can solve those problems. The fine particle fraction (FPF) represents the mass percentage of drug particles with an aerodynamic diameter below 5 μm, and is used for in vitro assessment of the aerodynamic properties of aerosols. Aerosol generation and in vitro deposition of particles is a complex process that depends on: the properties of the drug and carrier particles, assay conditions, and inhaler characteristics.1,2 Carrier surface characteristics strongly influence adhesion and severance of the particles in a drug. For effective drug delivery, interactions between the drug and carrier have to be powerful enough to produce a homogeneous formulation and at the same time not too potent to liberate drug particles during inhalation. Carrier particles with a rough surface have more binding sites to attach drug particles and less pronounced interactions between particles.3,4 Surface attributes can be quantified and applied in model development with use of tools created by Chinga et al and images from a scanning electron microscope (SEM).5
During recent years, there have been several publications about model development for prediction of particle deposition. Vinchurkar et al6 used a computational fluid dynamics method to model a Mark II Andersen cascade impactor (ACI) and applied it to evaluate the effects of charge on deposition of particles. A commercial computational fluid dynamics code was used for the flow field simulation. The model was validated based on predictions for cut-off d50 diameters for each of eight ACI stages.Kaialy et al7 analyzed factors that influence the FPF in a formulation composed of various types of commercial lactose and salbutamol particles. They found that the elongated, more irregular shape, and rougher surface of the carrier resulted in higher FPF values. The authors used only simple shape and surface factors calculated based on the length and breadth of the carriers. Chen et al8 combined computational fluid dynamics and the discrete element method for simulation of the transport and deposition of spherical particles in the computer model of a three-generation pulmonary airway. These authors used only two physical parameters of particles, like size and density for predictions of FPF. Sturm and Hofmann9 presented a system for predicting extrathoracic, bronchial, and alveolar fiber deposition in the human respiratory tract based on breathing conditions, fiber properties, and the morphometric lung model. In most cases, the models available can predict in vitro deposition for a system composed of one type of particle (drug or carrier), and use only one or two formulation-related factors, like the charge, dimensions, or density of the particles. There is a lack of a general model that could support the formulation development process for carrier-based pulmonary delivery systems.
Artificial neural networks and genetic programming methods have been successfully employed for modeling purposes in pharmaceutical technology, eg, prediction of dissolution profiles,10 in vitro-in vivocorrelation,11 and prediction of pellet properties.12 The modeling approach was presented as a useful method during construction of expert systems to support formulation development process.13 The present study introduces the concept of using empirical modeling based on data in the literature to obtain a predictive model for in vitro deposition of drug particles. The methodology is based on selection of important variables and advanced modeling tools like artificial neural networks, genetic programming, rule-based systems, and fuzzy logic. The prepared models are validated on a new experimental data set.
Materials and methods
Data set
The database was acquired from the literature. Scientific articles were scanned and included in the analysis based on the following criteria: detailed information about drug and carrier (name and particle size); availability of an SEM image of the carrier; and description of assay conditions (flow rate, impactor and inhalator type).
After review of approximately 800 papers from the Scopus and PubMed databases, eleven met the inclusion criteria. The created database contained information about FPF for three various impactors, ie, the ACI, the next-generation impactor, and the multi-stage liquid impinger. A detailed list of the source publications is included in Table S1. Formulations were composed of five different types of substances as carriers, ie, trehalose, mannitol, lactose, erythritol, and hydroxyapatite. Based on the SEM pictures of carriers, 13 variables describing surface properties were calculated, including the arithmetical mean deviation, root mean square deviation, skewness of the assessed profile (Rsk), kurtosis of the assessed profile, lowest valley, highest peak, total height of the profile, average height of an unleveled surface, mean polar facet orientation, variation of the polar facet orientation, direction of azimuthal facets, mean resultant vector, and surface area.14 The carrier shape analysis was performed based on SEM pictures using ImageJ,15 as described in the section on surface and shape analysis. The procedure resulted in six parameters describing the shape of carriers: the circularity, longest distance between two points (Feret), angle between the Feret’s diameter and a line parallel to the x axis of the image (FeretAngle), minimum caliper diameter (MinFeret), ratio between particle height and particle width, and roundness.16 The database contained information about formulations composed of nine active pharmaceutical ingredients (API), ie, salbutamol, budesonide, ciprofloxacin, cyclosporine A, disodium cromoglycate, fluticasone propionate, formoterol fumarate, ipratropium bromide, and salmeterol. The chemical structure and properties of the drug molecules were encoded by chemical descriptors computed using Marvin cxcalc plugin, UK (version 6.1; ChemAxon, Budapest, Hungary)17 based on three-dimensional optimized structures. Moreover, the mass percentage of API in the formulation, the carrier, and the API particle size distribution, inhaler device type (Novolizer®, Aerolizer®, Rotahaler®, powder dispatchment tube, SetA, SetD), flow rate (L/min) during the experiment, were included according to data found in the articles. The complete structure of the database is shown in Table 1 and the full database is available in Table S2. Overall, there were 91 data records with 136 variables. The FPF was the only dependent variable and the other 135 input variables contained information about the carrier, drug, and assay conditions. The data set was processed to reduce the size of the input vector and to split data according to the 10-fold cross-validation method to check the generalization ability of the models created and simulate their real application to predict in vitro deposition for new formulations and unknown conditions.
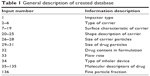  | Table 1 General description of created database |
Surface and shape analysis
The surface analysis was performed based on the SEM photographs using the SurfCharJ14 plugin for ImageJ (version 1.47n), which allows calculation of parameters quantifying surface roughness. All parameters are described in the “data set” section of this article. Prior to analysis, each picture was standardized in terms of scale and grayscale depth (32-bit). Ten randomly chosen square sections of the particle surface with a size of 10 μm ×10 μm were analyzed. Surface roughness was calculated with standard settings of the SurfCharJ plugin with an additional “level surface” option, which allows alignment of the surface by subtracting a regression plane from the surface. The final results for each particle were the average of ten samples. The carrier shape study was performed using ImageJ standard tools for a particle analysis with manual marking of each particle.
Selection of features
The aim of the feature selection was to reduce the number of inputs in the database before the modeling process in order to simplify the models created, to find the most important variables, and to save time and computational resources. The feature selection was performed by “fscaret”18 for R environment (The R Foundation for Statistical Computing, Vienna, Austria).19 The main parameters of the method used are listed in Table 2. The results are presented as a ranking of variables with a calculated importance value for each variable. Cut-off points for creation of new databases were set at a 5% gradient decrease.
  | Table 2 Settings for selection of variables performed by fscaret |
Model assessment
Model goodness of fit was expressed as root-mean-squared error (RMSE, equation 1) and normalized root-mean-squared error (NRMSE, equation 2).
| (1) |
where obsi and predi are the observed and predicted values, respectively, i is the data record number, and n is total number of records.
| (2) |
where RMSE is the error calculated for model, Xmax is the maximum value of the observed results, and Xmin is the minimum value of the observed results.
Artificial neural networks
Multilayer perceptron neural networks were created using a “monmlp”20 package for R environment. All of the prepared models had two hidden layers, each one numbering from 4 to 50 nodes. The transfer function for the hidden layer was set as a hyperbolic tangent (tansig), and the linear function was applied for the output layer. Ensemble systems were employed and contained ten or 20 neural networks. Variables were scaled from 0.1 to 0.9, and iteration numbers were set to 10, 50, 80, 100, 200, 400, 500, 800, and 1,000. The multistart technique was used in order to avoid local minima: the “trials” parameter was set to 5.
Rule-based systems
For modeling purposes, two rule-based systems were used, ie, “randomForest”21 and “Cubist”.22 The first one creates models based on a forest of decision trees using random inputs. The following parameters were used during the modeling process: automatic selection number of variables, maximum number of nodes set as 1,000, and number of trees set from 1 to 100. Cubist also creates regression models in a manner of decision trees, but it introduces linear equations at their terminate branches. During the modeling process, the maximum number of rules was fixed at 100, and the number of committees was set from one to 100. The extrapolation parameter, which controls the estimation ability of created models beyond the original observation range, was set to 100. The sample parameter, which is a percentage of the randomly selected data set for model building, was established at zero, which means that no data subsampling was employed and all the models were built on the complete data sets available for each run.
Fuzzy systems
Package for R environment “fugeR”23 was used to create models based on fuzzy logic rules. This tool uses a genetic algorithm to build a fuzzy system based on a given training data set. At the beginning, the system generates a random population and tests it on the available data. Afterwards, the best models are used to generate a new population based on genetic operators like crossover and mutation. The maximum number of rules was set to 3, 40, 50, or 100 (“maxRules”). The maximum number of input variables per rule was set from two to five. The population size was varied from 100 to 5,000.
Genetic programming
Mathematical models were produced with the genetic programming system available from the “rgp”24 package of the R environment. The package implements symbolic regression, a method that allows automatic construction of a mathematical formula by evolutionary algorithms based on experimental data. The model obtained is of a white-box type, so the results are easier to interpret in comparison with artificial neural network models. The size of the chromosome, which is a representation of the maximum length of the equation, was varied from 5 to 100. The more complex the equation, the higher the probability of its overfitting and weak generalization ability, thus the final choice of the optimal model is always a trade-off between its complexity and best achievable goodness of fit criterion. The population size was set to 1,000 and the modeling process was set to 500 million evolution steps divided into 100 stages. After each stage, the models were tested according to the 10-fold cross-validation method. Apart from maximum evolution steps, minimum training error (RMSE) was set as an additional algorithm stop condition. According to the previous results (monmlp, randomForest, and Cubist), its value was established as 5. The genetic programming method was applied to the original database to find the mathematical relationship between FPF, formulation properties, and assay conditions. After selecting the best model, its parameters were optimized to assess the generalization ability. For optimization purposes, the “optimx” package for R environment was used.25The general scheme of work and the models are presented in Figures 1 and 2.
  | Figure 1 Scheme of work. |
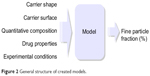  | Figure 2 General structure of created models. |
Hardware environment
All calculations were performed using 27 workstations with a total of 304 threads working under the openSUSE 13.1 operating system.
Results and discussion
Selection of important variables
The results of the fscaret package were used for selection of the most important variables. Based on this method, 51 new data sets were prepared, containing from 4 to 46 input variables.26 These data sets were used in a further modeling process using artificial neural networks, Cubist and randomForest tools in the 10-fold cross-validation mode. The best model in terms of generalization ability was found for the input vector of 28 variables (Table 3). The most numerous group of selected variables described drug properties, especially electronic characteristics, such as water accessible surface area (ASA), logP, and hydrogen donor bond count at pH 12. According to the definition of logP, hydrophilic substances have a low partition coefficient value and they are more soluble in water than in n-octanol. Hydrophobic substances have a high logP value and their solubility in water is lower than in n-octanol. Chuman et al27 created a model for calculation of logP based on solvation energy and ASA. It could be observed that molecules with a low ASA value are more hydrophilic than chemical compounds with a high ASA.
In conclusion, ASA and logP values are associated with hydrophilic properties of substances related to their dipole moment, thus accounting for the electrostatic behavior of particles. According to Pilcer et al2 the latter could be important for drug-carrier interactions in the same way that van der Waals forces are important. It could also be hypothesized that the drug’s hydrogen donor bond count at pH 12 is probably related to the pKa value of carriers, which in most cases in the collected database is between 12 and 13. This may strengthen our earlier conclusion about the importance of electrostatic interactions between carrier and drug particles. Since no data about the actual charge on the particle surface were available, our reasoning is indirect and based on the assumption that the properties of a chemical compound influence and/or determine the properties of particles containing chemical substance as a main component. The other group of descriptors depicts the surface and shape of the carrier. Both factors are important for deposition of particles and influence adhesion forces between particles. There is still no clear explanation of how surface roughness can influence aerosol performance. Several authors have reported contradictory observations, ie, that both smooth and rough surface of the carrier was beneficial for particle deposition.2,28 Based on those results, it may be hypothesized that the performance of an aerosol is not only related to the roughness of the particles, but is also linked to the shape of spikes and valleys observed on the carrier surface, as these variables were also included in our best model. These findings need further investigation. It was also found that assay conditions like flow rate, type of inhaler device, and impactor type can affect particle deposition.29,30
Modeling
Based on 10-fold cross validation scheme, new data sets with reduced number of inputs were divided into learn-test pairs. A total of 51 different input vectors were used at the first stage of modeling by Cubist, randomForest, and monmlp packages for R environment. The best results were obtained for 28 input vectors for artificial neural network-based models with RMSE and NRMSE equal to 5.76 and 13%, respectively. A comparison of the best models created for all modeling methods is shown in Table 4. Thus, a further modeling process with a genetic programming method and fuzzy systems was performed using 28 input vectors. The structure of the data set is presented in Table 3. Models created using rule-based systems like Cubist and randomForest showed an NRMSE error that was slightly higher than artificial neural networks (by 3% and 2%, respectively). The best fuzzy logic model had an RMSE and an NRMSE of 5.5 and 12%, respectively. The mathematical model was characterized by an RMSE of 4.9. Moreover, the genetic algorithm performed further automatic input vector reduction, ending up with only eleven input variables selected from the database (Equation 3). The observed versus predicted plot for the model is presented in Figure 3.
  | Figure 3 Observed versus predicted plot for model created with the genetic programming method. |
| (3) |
where In1–In28 corresponds to the labels in Table 3 and C1–C2 are constants. The equation parameters are C1 =23.84648 and C2 =3.456648.
As a summary of the modeling step, the architecture and settings of the created models are shown in Table 5. A more complex mathematical equation derived as an additional model is presented in Table S3. Additionally, GUI-based software implementing the presented models was written in Java and published for free download from the Internet (the details are presented in Table S4).
  | Table 5 Architecture and settings of created models for various modeling methods |
The features selected for FPF prediction utilize information on drug properties (three variables), assay conditions (two variables), drug content in the formulation, and the properties of the carrier, including surface, type, and particle size. Further analysis of Equation 3 revealed that in vitro deposition as predicted by the model increases together with flow rate and decreasing drug content in the formulation (Figure 4B). Steckel and Müller31 showed that, in most cases, the FPF decreases when the drug content in the formulation increases. Experimental results show that an increased flow rate results in a higher FPF.32–34 The Rsk variable was found to be important for prediction of the FPF. It is asymmetry measure of the probability distribution of surface profile and is a more complex parameter than other surface descriptors, eg, the arithmetical mean deviation, root mean square deviation, lowest valley, highest peak, and total height of the profile.5 A positive value of Rsk indicates preference of low areas on the surface whereas a negative value of Rsk indicates domination of highly elevated surfaces. An Rsk value close to zero means that the distribution of height values is similar to a normal distribution. Moreover, according to the plot of Rsk versus FPF (Figure 4A), it can be observed that a surface with a low Rsk value (Figure 5C and D) has narrow valleys and rough spikes. This could impede interaction between carrier and drug particles. In the case of a higher Rsk, valleys on the particle surface are wider (Figure 5A and B), so could provide a better chance for interactions between drug and carrier particles. There is a need for further experiments to explain the influence of the surface topology of the carrier on drug-carrier interaction. Further, according to Equation 3, the more hydrophilic the API, the lower the FPF that can be achieved. This finding is probably related to the dipole moment, which is crucial for the strength of van der Waals forces between particles. It is known that a more hydrophilic substance has a larger dipole moment.
Validation
The final mathematical model (Equation 3) was tested on new experimental data from the College of Engineering, Nanyang Technological University, Singapore. A new formulation composed of a hydroxyapatite carrier (Figure 6) and budesonide as a model drug was tested in an ACI impactor. Before validation, the parameters of Equation 3 were optimized based on the complete data set gathered from the literature, so no further cross-validation (10-cv) was employed. The validation data set was prepared according to the described methodology and all inputs used for calculation are shown in Table 6. The results are summarized in Table 7. FPF values predicted for a flow rate of 30 L/min and 60 L/min were 14.50% and 23.16%, respectively. The RMSE and NRMSE calculated for the external validation data set were 3.8 and 8.6%, respectively. The obtained results indicate that the created model is reliable.
  | Figure 6 Scanning electron micrograph of hydroxyapatite carrier for additional formulation. |
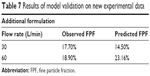  | Table 7 Results of model validation on new experimental data |
Conclusion
In this study, an approach to empirical modeling based on data in the literature was developed. All stages of the experiment, eg, shape and surface analysis, feature selection, and modeling, were performed using open source software available to everyone for free.19 As a result, the model described by the classical mathematical equation for prediction of in vitro deposition based on characteristics of formulation and assay conditions was obtained. A modeling technique like genetic programming can be useful for modeling of complex processes such as in vitro deposition. The feature selection led to reduction of the input variables from 135 to 28. During development of the model, three key elements were applied:
- SurfCharJ plugin and the ImageJ program, which allowed calculation of the carrier’s surface and shape descriptors based on SEM images
- Marvin, a tool for computation of molecular descriptors
- Tools for feature selection and modeling.
The validation of the model confirmed its applicability for development of new inhalation formulations and decision support systems.
Acknowledgment
This work was funded by a bilateral Poland-Singapore cooperation project (2/3/POL-SIN/2012).
Disclosure
The authors report no conflicts of interest in this work.
References
Rahimpour Y, Hamishehkar H. Lactose engineering for better performance in dry powder inhalers. Adv Pharm Bull. 2012;2(2):183–187. | ||
Pilcer G, Wauthoz N, Amighi K. Lactose characteristics and the generation of the aerosol. Adv Drug Deliv Rev. 2012;64(3): | ||
Hassan MS, Lau R. Inhalation performance of pollen-shape carrier in dry powder formulation: effect of size and surface morphology. Int J Pharm. 2011;413(1–2):93–102. | ||
Hassan MS, Lau RWM. Effect of particle shape on dry particle inhalation: study of flowability, aerosolization, and deposition properties. AAPS Pharm Sci Tech. 2009;10(4):1252–1262. | ||
Chinga G, Johnsen PO, Dougherty R, Berli EL, Walter J. Quantification of the 3D microstructure of SC surfaces. J Microsc. 2007;227 Pt 3: 254–265. | ||
Vinchurkar S, Longest PW, Peart J. CFD simulations of the Andersen cascade impactor: Model development and effects of aerosol charge. J Aerosol Sci. 2009;40(9):807–822. | ||
Kaialy W, Ticehurst M, Nokhodchi A. Dry powder inhalers: mechanistic evaluation of lactose formulations containing salbutamol sulphate. Int J Pharm. 2012;423(2):184–194. | ||
Chen X, Zhong W, Zhou X, Jin B, Sun B. CFD–DEM simulation of particle transport and deposition in pulmonary airway. Powder Technol. 2012;228:309–318. | ||
Sturm R, Hofmann W. A computer program for the simulation of fiber deposition in the human respiratory tract. Comput Biol Med. 2006;36(11): 1252–1267. | ||
Szlęk J, Pacławski A, Lau R, Jachowicz R, Mendyk A. Heuristic modeling of macromolecule release from PLGA microspheres. Int J Nanomedicine. 2013;8:4601–4611. | ||
Mendyk A, Tuszyński PK, Polak S, Jachowicz R. Generalized in vitro-in vivo relationship (IVIVR) model based on artificial neural networks. Drug Des Devel Ther. 2013;7:223–232. | ||
Mendyk A, Kleinebudde P, Thommes M, Yoo A, Szlęk J, Jachowicz R. Analysis of pellet properties with use of artificial neural networks. Eur J Pharm Sci. 2010;41(3–4):421–429. | ||
Mendyk A, Jachowicz R. Unified methodology of neural analysis in decision support systems built for pharmaceutical technology. Expert Syst Appl. 2007;32(4):1124–1131. | ||
SurfCharJ plugin for ImageJ. Available from: http://www.gcsca.net/IJ/SurfCharJ.html. Accessed January 1, 2014. | ||
Rasband WS. ImageJ. Bethesda, MD, USA: National Institutes of Health. Available from: http://imagej.nih.gov/ij/, 1997–2014. | ||
Particle analysis with ImageJ. Available from: http://rsb.info.nih.gov/ij/docs/menus/analyze.html. Accessed June 1, 2014. | ||
Marvin ChemAxon. Available from: http://www.chemaxon.com. Accessed January 1, 2014. | ||
Szlęk J. fscaret: automated caret feature selection. Available from: http://cran.r-project.org/web/packages/fscaret/index.html. Accessed June 1, 2014. | ||
R Core Team. R: a language and environment for statistical computing. Vienna, Austria: The R Foundation for Statistical Computing. Available from: http://www.R-project.org/. Accessed June 1, 2014. | ||
Cannon AJ. monmlp: monotone multi-layer perceptron neural network. Available from: http://cran.r-project.org/web/packages/monmlp/index.html. Accessed June 1, 2014. | ||
Liaw A, Wiener M. Classification and regression by randomForest. R News. 2002;2(3):18–22. | ||
Kuhn M, Weston S, Keefer C, Coulter N. C code for Cubist by Ross Quinlan. Cubist: Rule- and Instance-Based Regression Modeling. R package version 0.0.18. Available from: http://CRAN.R-project.org/package=Cubist. Accessed June 1, 2014. | ||
Bujard A. fugeR: FUzzy GEnetic, a machine learning algorithm to construct prediction model based on fuzzy logic. R package version 0.1.2. Available from: http://CRAN.R-project.org/package=fugeR. Accessed June 1, 2014. | ||
Flasch O, Mersmann O, Bartz-Beielstein T, Stork J, Zaefferer J. rgp: R genetic programming framework. Available from: 0.4-0. http://CRAN.R-project.org/package=rgp. Accessed June 1, 2014. | ||
Nash JC, Varadhan R. Unifying optimization algorithms to aid software system users: optimx for R. J Stat Softw. 2011;43(9):1–14. | ||
Szlęk J. A short fscaret package introduction with examples. Available from: http://cran.r-project.org/web/packages/fscaret/vignettes/fscaret.pdf. Accessed August 28, 2014. | ||
Chuman H, Mori A, Tanaka H, Yamagami C, Fujita T. Analyses of the partition coefficient, log P, using ab initio MO parameter and accessible surface area of solute molecules. J Pharm Sci. 2004;93(11): 2681–2697. | ||
Kou X, Chan LW, Steckel H, Heng PWS. Physico-chemical aspects of lactose for inhalation. Adv Drug Deliv Rev. 2012;64(3):220–232. | ||
Demoly P, Hagedoorn P, de Boer AH, Frijlink HW. The clinical relevance of dry powder inhaler performance for drug delivery. Respir Med. 2014;108(8):1195–1203. | ||
Taki M, Marriott C, Zeng X-M, Martin GP. Aerodynamic deposition of combination dry powder inhaler formulations in vitro: a comparison of three impactors. Int J Pharm. 2010;388(1–2):40–51. | ||
Steckel H, Müller B. In vitro evaluation of dry powder inhalers II: influence of carrier particle size and concentration on in vitro deposition. Int J Pharm. 1997;154:31–37. | ||
Hassan MS, Lau R. Inhalation performance of pollen-shape carrier in dry powder formulation with different drug mixing ratios: comparison with lactose carrier. Int J Pharm. 2010;386(1–2):6–14. | ||
Coates MS, Chan H-K, Fletcher DF, Raper JA. Influence of air flow on the performance of a dry powder inhaler using computational and experimental analyses. Pharm Res. 2005;22(9):1445–1453. | ||
Hoe S, Traini D, Chan H-K, Young PM. The contribution of different formulation components on the aerosol charge in carrier-based dry powder inhaler systems. Pharm Res. 2010;27(7):1325–1336. |
 © 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2015 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.