Casual effect of methotrexate+etanercept/infliximab on survival of patients with rheumatoid arthritis

Introduction

Rheumatoid arthritis (RA) is a chronic inflammatory disease, which, in many patients, leads to a substantial disability and has a major effect on the quality of life. RA patients encounter with an increase in mortality respect to the general population, mainly due to cardiovascular disease and infections, respiratory disease, and some malignancies.^1,2 Causes of premature death and their associated risk factors include major inflammation, disability and severe extra-articular disease manifestations.^1,2 Effective treatment decreases the risk of comorbidity and premature mortality and increases the survival of the patients. Comparing the effect of biologic disease-modifying antirheumatic drugs (DMARDs) with conventional DMARDs on survival of RA patients has been controversial, and it needs some other studies to find the casual effect.^3–5

A clinical trial is the ideal way to determine causal effect. However, in some cases, it is not possible to carry out a clinical trial or the costs are prohibitive. In these cases, observational studies are being used and the causal effects are estimated via propensity scores.^6,7

Sometimes, covariates are measured at different time points in survival studies. Therefore, an appropriate approach should be employed to control time-dependent variables in order to achieve a causal relationship.^8,9 In survival studies, time-dependent predictors of survival that are also predictors of subsequent therapies are called time-dependent confounders.^10–12 Indeed, these variables are sometimes mediators.^8,9,12 The confounders should be adjusted, but adjusting based on the mediators does not take the indirect effect of treatment on survival into consideration.^9,12 To overcome this problem, the use of propensity score method has been suggested.^6,13 The challenge in employing the given method in studies that have time-dependent covariates have been further answered via marginal structural models (MSMs).^10,14–17 Various studies have also utilized the method introduced by Hernan et al to embed a time-dependent confounder in the Cox model.^18–24 In this approach, the survival model is approximated with the pooled logistic regression model.¹¹ Accordingly, time is divided into small intervals so that the probability of occurrence of the event at these intervals decreases. But, this method was encountered by some limitations.²⁵ The first one is that the intervals must be such that the probability of occurrence of the event at these intervals should be small; otherwise, the approximation will not be appropriate. The second problem is that, for all these small intervals, the time-dependent confounder must be measured which is not usually determined due to being time-consuming or even not cost-effective. Therefore, alternative methods should be used to solve these problems.²⁵ The method introduced in this design is piecewise constant baseline hazard model. In this way, the survival time is divided into several pieces and the model is weighted via calculated weights.^11,26

Patients and methods

Patient population and inclusion criteria

In this cohort study, analyses were directed toward patients with physician-diagnosed RA based on 1987 American College of Rheumatology Classification Criteria and referred for treatment to the Rheumatic Diseases Research Center in the city of Mashhad, Iran, from October 2008 to March 2016. This study was approved by the Ethics Committee of the School of Public Health, Tehran University of Medical Sciences, Iran (Approval No. IR.TUMS.SPH.REC.1395.777) and also complied with the requirements of the Helsinki Declaration. To participate in this study, written informed consent was obtained from all the study subjects.

A total number of 512 RA patients with 3.06±1.56 visits to the research center per year were enrolled. All the patients had received at least 6 months of methotrexate (MTX) treatment with varying doses (10–25 mg per week). The MTX therapy for 62 patients had been also supplemented with etanercept/infliximab (ETA/INF) because of poor responses (Disease Activity Score 28 more than 2.5 or existence of abnormal laboratory findings or gastrointestinal complications, after at least 6 months of treatment with MTX or its increased dose) to the initial intervention. Among the subjects, 62 individuals were administered by MTX+ETA/INF. All other patients treated with biologic DMARDs, other than INF and ETA, were excluded from the analyses. The doses of INF and ETA were 3 mg/kg and 50 mg per week, respectively. For MTX+INF-treated patients, the dose of steroid was 5–7.5 mg daily and 20 mg every other month. Indeed, according to the guidelines for prescribing MTX and biologic agents, patients with current or past viral hepatitis history were removed from the study.

Drug exposure definitions

Drug categories included individual MTX (EBEWE, Unterach, Austria) and all other nonbiologic DMARDs, such as sulfasalazine (SSZ [Mehr Darou, Tehran, Iran]) and hydroxychloroquine (HCQ [Rouz Darou, Tehran, Iran]). As previously stated, INF/ETA was added to the treatment regimen where patients exhibited inadequate responses to MTX. The survival rate of patients receiving MTX was also compared with that of individuals whose treatment was supplemented with INF (JANSSEN, Leiden, Netherlands) or ETA (Pfizer, Berlin, Germany).

Statistical methods

The quantitative variables were described as mean±SD or median (IQR), and the qualitative variables were described in counts and percentages. A Chi-square test was also conducted to compare gender, employment, and rheumatoid factors (RFs) of the MTX and MTX+ETA/INF groups. Age and disease duration were similarly compared between groups using independent sample t-test and Mann–Whitney U test, respectively. The linear mixed-effects model was also employed to assess changes in HCQ and SSZ over time between groups.

In this study, the duration of the follow-up was divided into two parts, less than 1 year and more than 1 year. After that, piece-wise constant baseline hazard model was fitted to the data and the effect of treatment was obtained.^26,27 Then, for each person-time, propensity scores were calculated.¹¹ Covariates used to calculate the propensity scores included gender, age, body mass index (BMI), job, RF+, anti-cyclic citrullinated peptide+ (anti-CCP+), number of visits, follow-up duration, cumulative MTX dose and pain score as a time-dependent confounder, measured by VAS. These propensity scores were used in the piecewise constant baseline hazard model via MSM, and the effect of treatment was reestablished, and the results of these two models were compared. The R3.3.3 was employed to fit these models to the data.²⁸ Maximization was also done by optimization command for different initial values.

Results

According to the baseline data, the mean age was 47.75±13.90 years and 431 (85.2%) of the patients were women. Among all the patients, 392 (77.6%) of them were housekeepers, 78 (15.4%) of these individuals were office employees, and 35 (6.9%) of the subjects had other types of employment. Additionally, 438 (85.5%) and 396 (77.3%) were positive for RFs and anti-CCP, respectively. Indeed, 55 (10.8%) of patients were smokers, 86 (16.8%) had diabetes, 157 (30.7%) hypertension, 85 (16.6%) obesity, 179 (35%) hypercholesterolemia, 154 (30%) high level of low-density lipoprotein, 230 (44.9%) low level of high-density lipoprotein and 135 (26.4%) high triglycerides. The IQR follow-up per person was 12 (26.75) months.

As illustrated in Table 1, the results of the Chi-square test showed that the distributions of gender, employment, positive RF, and anti-CCP were nonsignificantly different between groups (p=0.262, p=0.751, p=0.262, p=1, p=0.418, respectively). Moreover, age and follow-up duration did not significantly differ between groups (p=0.452 and p=0.550, respectively).

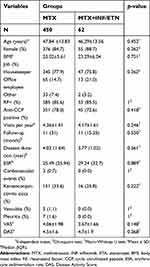Table 1 Baseline and disease characteristics in patients receiving MTX, MTX+INF, and MTX+ETA

Changes in HCQ and SSZ were assessed by the linear mixed-effects models. In this regard, no significant difference was found between the study groups (p=0.368 and p=0.848, respectively).

The percentage of deaths in the MTX+ETA/INF group was 14.51% vs the value of 16.89% in the MTX group. The 8-year survival rates for patients in MTX+ETA/INF vs MTX groups were 70% and 68% (Figure 1), respectively. According to Table 2, the base model showed that MTX+INF/ETN could significantly reduce the HR (HR=0.789, 95% CI [.634, 0.983]). After adjusting by time-dependent confounder via MSM, HR was not significantly different in two groups (HR=0.968, 95% CI [0.860, 1.090]). Moreover, Akaike information criterion revealed that Model 1 had better fit to the data than the base model.

Table 2 Parameter estimation for piecewise constant baseline hazard model and marginal structural piecewise constant baseline hazard model

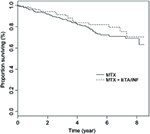Figure 1 Kaplan–Meier survival curve by groups.Abbreviations: MTX, methotrexate; INF, infliximab; ETA, etanercept.

Discussion

In this study, a marginal structural piecewise constant baseline hazard model was used to estimate the causal effect of MTX+ETA/INF on survival rates in patients with RA.^11,26 The standard methods to adjust time-dependent confounders which are predictors of previous treatment may also cause bias.^8,9 The crude effect of treatment on survival also showed that MTX+ETA/INF had a protective effect (HR=0.789, 95% CI [0.634, 0.983]). However, adjusted effect by time-dependent confounder (VAS) via MSM model demonstrated that HR was not significantly different between groups (HR=0.968, 95% CI [0.860, 1.090]). Accordingly, VAS was considered as a time-dependent confounder and also a mediator. Therefore, correct adjusting could lead to different results.

In a study assessing the relationship between anti-Tumour necrosis factor (anti-TNF) therapy and the survival of RA patients, 12,672 individuals as anti-TNF treated and 3,522 patients treated via nonbiologic drugs were monitored. Then, the survival rate of patients was evaluated with Cox proportional hazard model. Age, gender, severity of disease, disability index, and associated diseases were also adjusted by inverse probability of treatment weighting method. So, 9,445 and 50,803 person-years of follow-up were conducted for nonbiologic and biologic treatments, respectively. In this period, 204 deaths were reported for nonbiologic treated individuals and 856 cases for individuals treated with biologic agents. Adjusted hazard ratio and the 95% CI for all causes of death for biologic treatment with respect to nonbiologic drugs is 0.86 (0.64, 1.16) and unadjusted hazard ratio is by 0.74 (0.63, 0.86). This study showed that with a mean follow-up of 4 years, treatment with anti-TNF drugs was not related to increased or decreased mortality. In this study, the Kaplan–Meier graph was drawn only for the first 3 years of treatment and its long-term effects on survival were not illustrated. Conceivably, due to the short duration of follow-up, no significant difference was observed in the two groups.³

Contrary to the results of the present study, Carmona et al showed a relationship between TNF antagonists and survival of patients with RA, and this drug could significantly reduce mortality in these patients.⁴ The reasons for this result could be small sample size and low mortality rate (20 deaths) during the follow-up. Furthermore, one of the limitations of this study was that all confounders were not considered in the study and the results were adjusted based on age and gender. After adjusting for these variables, the mortality ratio of the control group compared with the TNF antagonist group was 0.32 (0.20, 0.53) for all causes of death.⁴

Jacobsson et al (2007) also reported that the adjusted HR for death by various variables was 0.65 (0.46, 0.93) for TNF antagonist group vs control group.⁵ In various studies, the combination of biologic drugs with MTX has been shown to improve the efficacy of these drugs and reduce the complications of MTX therapy.^29,30

The biggest challenge in these studies was to consider all confounding variables and to balance the differences between the two groups of patients receiving TNF antagonists and patients receiving nonbiologic drugs. Generally, patients receiving TNF antagonist drugs could suffer more severely from RA. In this case, the decision to receive or not to receive treatment was based on patient-related factors which could affect mortality. For this reason, there is a larger proportion of deaths in patients with severe RA associated with patients receiving TNF antagonists.

The inconsistency between the results of the present study and those in other investigations might has several reasons. First, all of the covariates required to adjust the impact of confounders might not be measured.⁸ Second, model misspecification could also cause different results. Third, because of the newness of biologic drugs and their unknown long-term complications, patients receiving these drugs needed to be carefully monitored, which could reduce mortality in these patients. Perhaps for this reason, previous studies had reported better survival rates for these patients.

One of the limitations of the present study was that a clinical trial had not been performed so far to compare the survival rates of patients receiving MTX and biologic agents, but cohort studies with large sample size did not show significant differences. Another limitation was that there was not a study evaluating the long-term effects of these drugs on survival. One other limitation of this study was that the cause of death was unclear. It should be noted that some specific causes might lead to different mortality ratios.