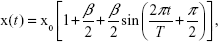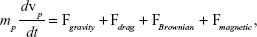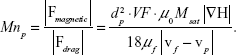Back to Journals » International Journal of Nanomedicine » Volume 11
Augmenting regional and targeted delivery in the pulmonary acinus using magnetic particles
Authors Ostrovski Y, Hofemeier P, Sznitman J
Received 9 December 2015
Accepted for publication 20 April 2016
Published 26 July 2016 Volume 2016:11 Pages 3385—3395
DOI https://doi.org/10.2147/IJN.S102138
Checked for plagiarism Yes
Review by Single anonymous peer review
Peer reviewer comments 2
Editor who approved publication: Dr Thomas Webster
Supplementary video 1 shows deposition fractions during the quiet breathing maneuver for the various particle types examined.
Views: 346
Yan Ostrovski, Philipp Hofemeier, Josué Sznitman
Department of Biomedical Engineering, Technion – Israel Institute of Technology, Haifa, Israel
Background: It has been hypothesized that by coupling magnetic particles to inhaled therapeutics, the ability to target specific lung regions (eg, only acinar deposition), or even more so specific points in the lung (eg, tumor targeting), can be substantially improved. Although this method has been proven feasible in seminal in vivo studies, there is still a wide gap in our basic understanding of the transport phenomena of magnetic particles in the pulmonary acinar regions of the lungs, including particle dynamics and deposition characteristics.
Methods: Here, we present computational fluid dynamics-discrete element method simulations of magnetically loaded microdroplet carriers in an anatomically inspired, space-filling, multi-generation acinar airway tree. Breathing motion is modeled by kinematic sinusoidal displacements of the acinar walls, during which droplets are inhaled and exhaled. Particle dynamics are governed by viscous drag, gravity, and Brownian motion as well as the external magnetic force. In particular, we examined the roles of droplet diameter and volume fraction of magnetic material within the droplets under two different breathing maneuvers.
Results and discussion: Our results indicate that by using magnetic-loaded droplets, 100% of the particles that enter are deposited in the acinar region. This is consistent across all particle sizes investigated (ie, 0.5–3.0 µm). This is best achieved through a deep inhalation maneuver combined with a breath-hold. Particles are found to penetrate deep into the acinus and disperse well, while the required amount of magnetic material is maintained low (<2.5%). Although particles in the size range of ~90–500 nm typically show the lowest deposition fractions, our results suggest that this feature could be leveraged to augment targeted delivery.
Keywords: inhalation medicine, targeted delivery, SPIONs, aerosol, CFD
Introduction
The lungs constitute the largest noninvasive pathway for drug delivery, with an exchange surface estimated at over 100 m2 in an average adult.1 This pathway is particularly attractive for treating lung diseases topically,2,3 including lung cancer,4 asthma, and obstructive diseases (eg, COPD). Moreover, from a systemic delivery perspective, it is the only available noninvasive delivery method for many drugs that cannot be orally administered due to their degradation in the digestive system (eg, proteins such as insulin).5–7
In past decades, there has been substantial progress in understanding respiratory fluid dynamics and the transport of inhaled therapeutic aerosols,8 including the physical (eg, aerodynamic) determinants affecting lung deposition outcomes.9 Nevertheless, the ability to target either a specific pulmonary region (eg, alveolar region) or a localized point within the airway tree (eg, lung tumors in the context of bronchogenic carcinoma) remains generally poor.10 Such a drawback leads to higher risks of side effects and lower bioavailability, which translates into inexact delivered doses to the target region.3 It has been recently hypothesized that these problems could be potentially alleviated through the incorporation of magnetic agents into the inhalable drugs, thereby controlling and improving aerosol deposition using externally applied magnetic fields.9,11
Recent preliminary in vivo studies in animals have strengthened the feasibility of such an idea. Perhaps, the best-known example is the work of Dames et al,12 where the authors demonstrated a local increase in lung deposition in rodents in the presence of a concentrated magnetic field. Namely, 3.5 μm droplets were nebulized with 3.5% v/v packaging of super paramagnetic iron oxide nanoparticles (SPIONs), leading to a 250% increase in deposition in the lung region exposed to the magnetic field. To further assess the feasibility of this method, they incorporated plasmid DNA into the droplets, along with the SPIONs and detected a twofold dose increase.11,12 From a toxicity standpoint, SPIONs are physiologically innocuous11–13 and have been shown to be safe as imaging contrast agents, as demonstrated by years of clinical use.14,15 Furthermore, these particles are easily manufactured in the form of liquid droplets, incorporating suspensions of SPIONs along with a wide range of therapeutics of choice.12 Importantly, magnetic particles can also be mass manufactured in a particulate form, eg, using spray-drying processes16,17 or emulsion evaporation methods.18
Following in the footsteps of Dames et al, more recent in vivo studies19,20 have also shown enhancement in lung deposition using magnetic particles. In parallel, studies on computational fluid dynamics (CFD) simulations have attempted to shed some light on the transport characteristics of these magnetic particles in the human lungs during inhalation.9 For example, Xi et al21 simulated the targeting of magnetic particles toward the olfactory region in the nasal airspace using a reconstructed patient-specific geometry. Pourmhran et al22 simulated magnetic particle deposition in a three-dimensional reconstructed tracheobronchial airway from computed tomography scans. Deeper down the conducting airways, Martinez et al23 simulated the behavior of ellipsoidal magnetic particles in models of symmetrical terminal bronchiole bifurcations.
Overall, computational studies have not only supported the idea of using magnetic particles for increased pulmonary deposition, but also helped deliver much-needed quantitative insight on magnetic particle behavior in extra-thoracic (eg, nose) and upper airways (eg, main and small bronchi). Despite such progress, there remains a gap in our understanding of the transport dynamics of inhaled magnetic aerosols in the deep acinar airways of the lungs, ie, a vast region made of hundreds of millions of sub-millimeter alveoli that constitute over 90% of total lung volume.24,25 Krafcik et al26 presented the first CFD simulations describing magnetic particle dynamics in the alveolar region, yet their study was limited to a single isolated alveolus modeled as a hemisphere, thereby omitting entirely the complex space-filling nature of the acinar tree morphology.27,28 Moreover, particle transport mechanisms such as diffusion were neglected in capturing realistic aerosol transport dynamics. A study has found that submicron particle dynamics and ensuing acinar deposition sites are highly affected by the coupling between intrinsic transport mechanisms (eg, diffusion) and local airflow phenomena as a result of the specific acinar topology.29 In particular, there remains a dearth of knowledge on the interplay of transport phenomena in the case of magnetic airborne particles, where potentially complex interactions between magnetic forces and convective, gravitational, and diffusive forces are anticipated within the acinar microenvironment. What constitutes optimized formulations of magnetic particles from an acinar deposition standpoint for increased bioavailability and systemic delivery remains to be answered.
Motivated by these shortcomings, using simulations, we revisited the problem of acinar aerosol delivery using paramagnetic aerosols. CFD–discrete element method (DEM) simulations of the dynamics of inhaled magnetic particles were investigated in an anatomically inspired, space-filling, multi-generation pulmonary acinar network under various inhalation maneuvers. Droplets loaded with different volume fractions (VFs) of SPIONs were modeled to screen for the influence of the exerted magnetic force. To cast this work more applicable in the context of practical therapeutic cases, various droplet diameters were examined using realistic nebulizer droplet sizes. Specifically, we addressed two different breathing maneuvers, quiet breathing (QB) and breath-hold (BH), and two different magnet operation scenarios in an effort to minimize the required external magnetic force. Using the simulation results, we explored what constitutes optimized magnetized particle formulations for acinar delivery.
Methods
Acinar domain and breathing motion
Morphometric studies have broadly described the underlying alveolar structure as constructed of polyhedral shapes with a single flat inter-alveolar septa separating adjacent airspaces.25,30,31 This morphology can be well described by space-filling octahedral shapes assembled into honeycomb-like structures.32 In accordance with recent CFD studies,27,29,33 an acinar tree consisting of repeating polyhedral units was constructed (Figure 1A), with up to six asymmetrically branching generations (Figure 1B). The tree extends on the scale of a few millimeters and consists of 343 polyhedra, of which 277 represent alveolar cavities, while the rest constitutes the acinar ducts (ie, the skeleton of the tree). The present geometry follows in the footsteps of Hofemeier and Sznitman,29 and a more detailed description can be found in their study.
While breathing motion is known to be asynchronous and spatially heterogeneous,34,35 the principle mode remains nevertheless self-similar.36 Hence, breathing was modeled by kinematically expanding and contracting the acinar domain using the following sinusoidal function:37
|
|
where x and x0 are the current and initial positions of each point on the wall, respectively, t is the time, β is the linear expansion factor (depending on the tidal breathing volume), and T is the breathing period. Depending on the breathing maneuver simulated (Results), the parameters β and T were modulated for an average human adult.33
Fluid and particle transport equations
Air inhaled into the acinus is assumed to be incompressible, Newtonian, and isothermal.38 The transient motion of air is governed by the continuity and Navier–Stokes equations adapted for volume changes over the breathing cycle.39 The respiratory oscillatory flow is mainly governed by two non-dimensional numbers, Womersley and Reynolds numbers. The peak Reynolds number in our domains reached up to Re = vf·d/υf ≤0.3 near the inlet (here, d represents the acinar diameter, vf is the fluid velocity, and υf is the kinematic viscosity), and dropped down orders of magnitude with increasing distal generation.37 Correspondingly, the Womersley number, defined as Wo = d·(ω/υf)0.5 (where ω =2π/T is the angular breathing frequency), represents the ratio between oscillatory inertia and viscous forces, and remained Wo <0.1 everywhere in the domain. Hence, the flow velocity was in phase with the pressure gradient and the flow behaved in a quasi-steady manner. These numbers agreed well with previously published data.38
For the boundary conditions, a no-slip condition was implemented on the domain walls and an arbitrary zero pressure condition on the inlet. It should be noted that in reality this pressure is lower (ie, during breathing, pressure in the alveolar regions is lower than the atmospheric pressure); however, the reference pressure does not affect the pressure gradients or the flow dynamics solved in the Navier–Stokes equations.29 For the inhaled aerosols, we implemented a Lagrangian framework governed by the force balance:
|
|
neglecting electrostatic, hygroscopic and other forces. Here, mp is the particle mass and vp is the particle velocity. The gravitational force (Fgravity) acts in the y-direction (Figure 1A), and the drag force (Fdrag) is modeled by Stokes’ drag law incorporating the Cunningham correction factor for air as the carrier fluid.38 The Brownian force that accounts for the stochastic motion of diffusive particles is given by the following equation:40
|
|
Here, Gi is a random vector with its components following a Gaussian distribution with zero mean and unit variance. Δt is the Brownian force time step and S0 is the spectral intensity, which is given by the following equation:
|
|
where kB is the Boltzmann constant, μf is the viscosity, and the subscript f represents the fluid phase, Tf =311 K is the body temperature, dp is the particle diameter, Cc is the Cunningham correction factor, and ρp is the particle density. Finally, the magnetic force acting on a particle is given by the following equation:41
|
|
where VF is the magnetic material volume fraction, χp is the magnetic susceptibility, μ0 is the permeability of free space, Msat is the magnetic material saturation, and H is the magnetic field strength, with Ĥ being its unit direction vector.
Particles enter the acinar domain through the inlet after 150 mL of air is inhaled into the lungs (representing ~5% increase in volume relative to the baseline functional residual capacity). This initial delay until injection represents the volume inhaled before particles have passed through the dead space (ie, conducting airways) and reached the acinar region. Once injected into the acinar domain, particles touching the wall are assumed to have deposited and hence cannot bounce back. Alternatively, particles that get exhaled through the domain exit (entrance) are not inhaled back during the following cycles.
Magnetic particles
Following the seminal work of Dames et al,12 water droplets (ρp=1000 kg/m3) were used as the inhaled (carrier) particles in our simulations. In an attempt to generalize the results presented, five distinct particle diameters were examined (0.5, 0.75, 1, 2, and 3 μm). For each size, up to ten different magnetic material VFs were considered (ranging from 0 to 40% v/v), yielding a total of 50 different examined particle types in each simulation; it should be noted that the density of the resulting SPION-loaded particles are adjusted according to VF. The magnetic material loaded into the simulated particles was magnetite (Fe3O4), ie, super magnetic iron oxide nanoparticles. These SPIONs42,43 have a mass density of ρmagnetic=5,175 kg/m3, a magnetic susceptibility of χ=20, and a magnetic material saturation of Msat=4.48·105 A/m. To externally manipulate the deposition of the particles, a realistic unidirectional magnetic field (Figure 1A for field orientation) of strength Hx=3.4×105 A/m or 0.43 T with a gradient dHx/dx=5.5·106 A/m2 was exerted; such parameters could correspond, eg, to a large 20×40 cm permanent magnet positioned adjacent to the patient and at a distance of ~11 cm away from the examined acinar geometry.43,44 Substituting these values back into Equation (5), we found that under such realistic conditions the particles are always magnetically saturated.41,45 It should be noted that given the relatively small dimensions of the acinar domain investigated (~1 mm), the selected magnetic field properties were assumed to be locally constant and unidirectional.43
Numerical methods
The acinar domain was meshed with tetrahedral cells using Ansys Gambit and refined in regions of high-velocity gradients (eg, near the inlet).29 The fluid motion was simulated using Ansys Fluent Finite volume solver, where a dynamic mesh function was implemented to expand and contract the domain. Rigorous convergence tests were performed to ensure that all numerical errors remained sufficiently low. Namely, mesh density, order and type of numerical models, time step, and residual numerical errors were all examined. As a result, a mesh of ~3 million cells was eventually selected, with a time step of 10−3 seconds. Moreover, we used a coupled pressure–velocity coupling scheme, a Green–Gauss node based for gradients, a body force weighted for pressure, a third-order MUSCL for momentum, and a second order for the transient formulation.39
To simulate the motion of particles, an in-house DEM solver was written and one-way coupled to the fluid. The particles were temporally integrated using an explicit first-order Euler model. Thorough convergence tests were performed on the DEM solver, after which a time step of 2×10−7 seconds was selected and 10,000 particles were used for each particle type to ensure good deposition statistics. It is important to note here that the time step implemented for the Brownian force, ie, Equation (3), was tuned independently of the fluid’s and particles’ time steps by using the expected root mean square velocity of the short time scales.46 As a result, the magnitude (and direction) of this force changes only once in two particle time steps. Particles were randomly injected from the domain inlet with parabolic weighting toward the inlet center and a uniform temporal distribution (until the end of inhalation). Finally, our DEM code was compared and validated according to established analytical models.29,35,47,48
Inhalation maneuvers
The feasibility of controlling particle deposition using SPIONs was first examined with a QB maneuver. In this simulation, β was 0.053 (representing a 16.8% expansion in lung volume about functional residual capacity) and the breathing period T was 3 seconds.29 As already mentioned, particles were injected after crossing the dead space; this corresponded here to ~0.6 seconds, ie, t/T=0.2, and the injection continued until exhalation (t/T=0.5).
In a following step, a breathing maneuver more common to drug administration was examined, ie, a deep breath followed by a BH. This maneuver was tested for two different magnet operation scenarios. In the first scenario, the magnet was constantly on during the drug administration (breath-hold type I [BH1]). In the second scenario, the magnet was on only during the BH (breath-hold type II [BH2]). In both described scenarios T=9.8 seconds and β=0.26, which represent a deep breath with 100% lung volume expansion. It should be noted here that the breathing cycle is divided into three parts, ie, inhalation that lasts for 2.4 seconds, a subsequent BH lasting for 5 seconds, and finally a 2.4-second exhalation.33 In such cases, the non-dimensional numbers (Re and Wo) remain on the same order of magnitude as in QB. As a result of the large volume expansion, flow rates are higher for the BH cases; for such cases, particles are accordingly injected at 0.41 seconds.
Results
Non-dimensional overview
For the range of particle sizes examined, the strongest force exerted on the droplets during inhalation was viscous drag. In the absence of the magnetic force, low flow velocities around the time of flow reversal (t/T ~0.5) allow either gravity or diffusion to become dominant for the largest and smallest particles, respectively, as previously discussed.29,38 By contrast, in the presence of a magnet, the magnetic force dominates over gravity and diffusion. To gain some intuition on the relative strength of the magnetic force on particle motion, we defined the ratio of the magnetic force to the drag force and thereby constructed a non-dimensional “particle magnetization number”:41
|
|
Using |vmax|≈0.4 m/s as the characteristic maximal velocity of the fluid at the domain inlet (retrieved from simulations), the magnitude of Mnp is plotted in Figure 2A and the corresponding values of the magnetic force are presented in Figure 2B (discussed further in the next section). The Mnp number is plotted against the different particle diameters examined, where the different lines represent the VF loading of SPIONs within droplets. It can be seen from Figure 2A that for the larger particles (ie, 3 μm and even 2 μm), the magnetic force is on the same order of magnitude as the peak drag force (Mnp ~0.1–1.0). It is thus anticipated that these particles will deposit very quickly in the direction of the magnetic field and will not be transported further into the acinar structure. For the smallest particles, on the other hand, Mnp is ~10−2 and thus the drag force dominates. Yet as the air flows toward distal generations, velocities fall quickly both spatially and temporally, thereby increasing the local Mnp. This number increases further once particles enter the alveolar cavity space, where local velocities are known to be several orders of magnitude slower compared to the flow in the acinar ducts.38
Acinar deposition
In the first step, the main metric that we seeked to improve was the drug deposition fraction in the acinus. Figure 3A presents deposition fractions during the QB maneuver for the various particle types examined; deposition is plotted as a function of particle diameter and the different lines represent varying VF loading of magnetic material in the droplets (for general visualization, Video S1; note that all particle types are mixed together, ie, different VFs and different diameters). It is seen that for particles with dp≥1 μm, a VF of 0.1 is sufficient to deposit nearly all particles. For dp=0.75 μm, a doubling of the VF is needed, whereas a fourfold VF increase is required for the smallest particles (dp=0.5 μm).
Hence, for the QB maneuver the amount VF of magnetic material needed for the smaller (<1 μm) particles is quite high, and should preferably be reduced. Hence, the BH1 maneuver was implemented (Figure 3B), which combines a deeper breath with a BH (Video S2). Compared to Figure 3A, we see that with no magnetization (ie, VF=0) all larger particles (2 and 3 μm) are now deposited, while the deposition of smaller particles increases about fourfold to fivefold. This result is not surprising as diffusion and sedimentation are given longer periods in the absence of convection to yield deposition; it is for this precise reason that a deep inhalation followed by a breath-hold is recommended as an effective administration method. In parallel, the influence of the magnetization becomes stronger as well; in Figure 3B deposition fractions for BH1 with VF=0.025 are comparable to those with VF=0.4 for a QB maneuver (Figure 3A). Hence, a deep breath combined with a BH maneuver dramatically reduces the amount of magnetic material needed and thereby the superfluous non-therapeutic material delivered. Comparing now the previous two cases with the BH2 case (Figure 3C), this latter maneuver is mainly implemented to improve the dispersion of particles across the acinar network, as discussed in latter sections (Video S3). Here, the main thing to notice is that despite the reduced magnet operation time, there is only a minor difference in deposition outcomes compared to BH1 (Figure 3B).
Particle dispersion
In parallel to deposition fractions, we next assessed the dispersion of the deposited aerosols as indicative of how well particles are able to reach and deposit across the acinar network. Deposition maps are presented in Figure 4 for representative particle diameters and VFs; particles are colored by the number of neighboring particles within a 50 μm radius (characteristic of the radius of an alveolus), effectively yielding a concentration map. It is to be noted that in order to achieve high dispersion, and thus avoid deposition “hot spots”, the average number of neighboring particles should be kept low with a uniform distribution across all particles. Looking at the first two rows of Figure 4 (corresponding to QB), we first observe the localized deposition of the larger 3 μm particles (ie, low dispersion), caused by the magnetic force, as anticipated from the large Mnp numbers. It should be noted, however, that such large particles may also deposit in more proximal airways (eg, terminal bronchioles) and not necessarily reach the acinus altogether. In contrast to the large particles, magnetized 0.5 μm particles under QB conditions penetrate deeper (though not reaching the distal generations) and deposit in large quantities, thereby dispersing relatively well. However, as seen from Figure 3A, a relatively high VF is required to achieve high deposition fractions. The 1 μm particles display a transition between the behaviors of the other two particle sizes, where deposition increases but dispersion is now biased toward airway branches aligned with the magnetic field.
We see from the first two rows of Figure 4 that under QB conditions, due to the superficial inhalation, particles do not have sufficient time to be carried into the most distal branches of the acinus after crossing the dead space. To overcome this limitation, the patient can be requested to inhale using a slow and deep breath;33 this deep breath maneuver is incorporated in both BH1 (Figure 4; third and fourth rows) and BH2 (Figure 4; fifth row). The third row shows the results of BH1 with VF=0 (ie, without the presence of a magnetic force), where a dramatic improvement in penetration depth is witnessed. All particles shown are now able to reach deeper into the acinus, where the smaller particles reach the last acinar generation. Comparing the results for BH1 (Figure 4; third and fourth rows), the dispersion problem is only slightly mollified for 3 μm particles; the magnetization reduces the dispersion once more and particles deposit quickly before the BH stage. For 0.5 μm particles, both the dispersion and penetration depth are improved when compared to the QB maneuver. Examining the effect of magnetization on these particles, they seem to penetrate deep but are locally biased toward the magnet.
The issue of penetration depth is improved through a deep breath maneuver, whereby a reduction of the required magnetic force (ie, required VF) is achieved through the use of a breath-hold. Nevertheless, 3 μm particles still deposit soon after injection, and are not conveyed inside with the deep breath. As mentioned earlier, the BH2 maneuver was hypothesized to improve such outcomes. Comparing the third and fifth rows (note that BH2 with VF=0 is identical to BH1 with VF=0), it is hard to identify noticeable differences by eye. Comparing the fourth and fifth rows, 3 μm particles penetrate much deeper and show better dispersion; these latter particles have reverted to being mainly biased by gravity.
In Figure 5, a quantification of dispersion is presented, where histograms shown on a logarithmic scale represent the average number of neighbors each particle has (error bars correspond to standard deviations). Statistical significance was calculated using a non-parametric Wilcoxon rank sum test for all possible pairwise combinations. We first mentioned that results for 0.5 μm particles in the QB maneuver are somewhat misleading and must be carefully interpreted since deposition fractions are considerably smaller than unity (~0.07, Figure 3A); in other words, fewer deposited particles lead to lower numbers of neighbors but do not necessarily coincide with better dispersion. Nevertheless, although for 0.5 μm particles it was previously hard to identify differences in the third, fourth, and fifth rows of Figure 4, we now see that all the three cases have significant differences in dispersion (Figure 5). Namely, out of the three, VF=0 shows the best results, while BH1 with VF=0.025 presents the worst. The 3 μm particles yield the poorest dispersion, with values of the average number of neighbors far exceeding all other particle sizes. This quantification also underlines that the results of BH1 with VF=0 (Figure 4; third row) and BH2 with VF=0.025 (Figure 4; fifth row) are indeed similar. Nevertheless, the VF=0 case is slightly better, as particles disperse well in the geometry but are locally pulled toward the magnet (Figure 4; fifth row). Lastly, we noted that for 1 μm particles, dispersion under QB with VF=0 is very similar to BH1 with VF=0 (no statistical significance with P=0.68, both cases are marked with # in Figure 5).
Discussion and summary
A previous numerical work on the dynamics of magnetic particles in the acinar regions has been based on a simple model of an alveolus falling short in capturing all the main aerosol transport mechanisms.26 Here, we attempted to deepen our understanding of the underlying transport phenomena of magnetic particles in the acinus. Our preliminary results exemplify how deposition efficiency could be increased with magnetic particles. Using a BH maneuver, the amount of magnetic material VF needed can be reduced; additionally, a good dispersion can be achieved if the magnet is turned on only during the breath-hold.
Before discussing further implications of our findings, we reviewed some of the limitations of our model. We utilized an idealized space-filling acinar domain constructed of repeating polyhedral shapes; as such, alveolar and ductal sizes as well as branching angles are constant, whereas the acinus is more heterogeneous in reality.25 Moreover, our domain represents only a small fraction of a total acinus, or even a characteristic sub-acinus comprising on the order of 103 alveoli.25 Recalling our boundary conditions, we modeled solely self-similar volume expansions that do not capture asymmetric effects,29 including heterogeneous alveolar recruitment or geometric hysteresis; this latter simplification is anticipated to influence dispersion outcomes. Finally, it is important to note that the deposition data presented here refers solely to the fraction of particles that deposit relative to those entering the acinar region; this may differ from the aerosol population found initially at the mouth opening. In spite of these limitations, we do not anticipate the general picture drawn in this work to be changed.
The well-established International Commission on Radiological Protection (ICRP) guidelines predict deposition fractions as a function of particle diameter across broad lung regions (eg, extra-thoracic, trachea-bronchial, and alveolar), following meta-analysis of empirical data.38 Among aerosol sizes acknowledged to deposit in the alveolar region, particles in the range of 90–500 nm yield the lowest total deposition in the lungs, with less than 10% deposition in the tracheobronchial and head airways combined.49 These particles are the least affected by Brownian diffusion or gravity; namely, they act as near tracers of the airflow (ie, confined to flow streamlines) and are thus essentially washed in and out of the lungs during breathing.29 As such, this particle size range has often been regarded as a poor choice for inhalation therapy.10,29,50 Here, instead our results underline how such size range in combination with noninvasive magnetic forcing can be leveraged for targeted deposition to the acinar region. In our proposed scenario, particles are first inhaled through a deep inhalation followed by the onset of a BH maneuver. At this point, such aerosols (90–500 nm) have not yet deposited and remain airborne. The magnet is then turned on, forcing them to rapidly deposit. We noted that after a deep inhalation, during the BH maneuver, the acinar region constitutes ~95% of lung volume; based on ICRP deposition plots,38 the vast majority (~90%) of inhaled particles are hence anticipated to deposit in the acinar region.
One application for such advocated method could be increasing the efficiency of deposited drugs. By achieving regional deposition in the alveolar regions alone, large quantities of wasted drug could be saved. Indeed, following our hypothesized scenario, aerosols would not be exhaled nor filtered in the upper airways. Looking at the ICRP deposition plot,38 we estimate that ~80% of the wasted drug could be saved. An alternative application for combining magnetic particles with our BH2 maneuver is to reduce side effects associated with upper airway deposition. Some drugs, while intended for the deep respiratory airways, cause severe side effects when depositing in upper airways. One such example is pentamidine, an antifungal drug, given once in 4 weeks. Although being an effective drug, due to its severe upper-airway side effects, this drug is used mainly in people who are allergic to other alternatives.51
It is also important to mention that the results presented here are not limited to the examined cases. We recall that the magnetic force is proportional to VF (Equation [5]); Figure 2B shows the magnitude of the magnetic force exerted on all the particle types simulated and may be used to infer general results; eg, a particle with VF=0.1 in a magnetic gradient that is two times weaker than in our simulations will behave exactly like a particle with VF=0.05, as presented here. Furthermore, assuming our acinar deposition results (Figure 2B) would be similar in any arbitrary acini throughout the lung (ie, notwithstanding heterogeneous ventilation, upper vs lower lobes, left vs right lobe asymmetry, etc), the spatial deposition throughout the lungs could be designed in principle by using the magnetic field distribution. This is not, however, without limitations; when using magnetic force, particle deposition near the lung walls closer to the static magnetic field will always be higher than deposition in the regions further away. In other words, this effect cannot be modified such that the magnetic field is stronger away from the magnet than near it; such a scenario would have been attractive for targeting of spatial points in the inner lung regions.
To cast our results in the context of targeted delivery to specific points in the acinus, we have first taken 0.5 μm particles as an example. Recalling Figure 3C, the deposition of the smallest particles investigated in the BH2 case was found to be ~40% with VF=0. This would suggest that there will be ~100% deposition in the acinar regions physically located nearest to the external magnet, while further away from the magnet, where the magnetic field is weaker, deposition would be likely closer to 40%. When concerned with targeted delivery, a ratio of 100% deposition at the specific point relative to near-zero deposition away from it would be optimal. Hence, for targeted delivery, we can explore the ratio of deposition fraction for the magnetized cases relative to the non-magnetized case (VF=0); optimizing such a parameter may be of greater use than increasing deposition alone. In Figure 6A, such ratios are presented for the regular breathing maneuver (QB), with values reaching up to 15 (depending on particle size and VF); by contrast, for the BH2 maneuver, values of the ratio approach 2.5 at most (Figure 6B). Hence, and perhaps surprisingly, a combination of small particles (90–500 nm) with a QB maneuver may be the most suitable choice (while keeping VF as low as possible). The relatively low targeting ratios presented in past in vivo works could be attributed to a suboptimal choice of particles (ie, sizes). For example, Dames et al12 used relatively large 3.5 μm droplets in rodents and achieved up to 2.5-fold increase in deposition. In line with existing in vivo results, in the future it would be interesting to examine the combinations advocated here.
Overall, our numerical simulations highlight how the transport of inhaled magnetic particles needs to be considered in the context of intrinsic particle dynamics (ie, convection, diffusion, sedimentation) and its coupling with particle size. In view of future in vivo experiments, our efforts will potentially bring forward novel inhalation strategies to achieve targeted aerosol delivery into the acinus. In particular, to the best of our knowledge, our results suggest for the first time that SPION-loaded droplets in the range of ~90–500 nm have the opportunity to act as attractive drug carriers. Moreover, high deposition fractions can in principle be achieved while maintaining low VF loadings for regional targeting of acini, whereas high deposition ratios could be realized in the context of localized point targeting.
Acknowledgments
The authors would like to thank the members of the Technion Biofluids Laboratory for helpful discussions. This work was supported in part by the Israel Science Foundation (grant no 990/12) and the European Research Council (ERC Starting Grant, grant agreement no 677772).
Disclosure
The authors report no conflicts of interest in this work.
References
Weibel ER. Morphometry of the Human Lung. 1st ed. Berlin: Springer; 1963. | ||
Burrowes KS, Doel T, Brightling C. Computational modeling of the obstructive lung diseases asthma and COPD. J Transl Med. 2014;12(Suppl 2:S5):1–8. | ||
Velkov T, Abdul Rahim N, Zhou QT, Chan HK, Li J. Inhaled anti-infective chemotherapy for respiratory tract infections: successes, challenges and the road ahead. Adv Drug Deliv Rev. 2015;85:65–82. | ||
Zarogoulidis P, Chatzaki E, Porpodis K, et al. Inhaled chemotherapy in lung cancer: Future concept of nanomedicine. Int J Nanomedicine. 2012;7:1551–1572. | ||
Patton JS, Bukar JG, Eldon MA. Clinical pharmacokinetics and pharmacodynamics of inhaled insulin. Clin Pharmacokinet. 2004;43(12):781–801. | ||
Patton JS, Byron PR. Inhaling medicines: delivering drugs to the body through the lungs. Nat Rev Drug Discov. 2007;6:67–74. | ||
Sakagami M, Byron PR. Respirable microspheres for inhalation: the potential of manipulating pulmonary disposition for improved therapeutic efficacy. Clin Pharmacokinet. 2005;44(3):263–277. | ||
Tsuda A, Henry FS, Butler JP. Particle transport and deposition: basic physics of particle kinetics. Compr Physiol. 2013;3:1437–1471. | ||
Longest PW, Holbrook LT. In silico models of aerosol delivery to the respiratory tract – development and applications. Adv Drug Deliv Rev. 2012;64(4):296–311. | ||
Kleinstreuer C, Zhang Z, Donohue JF. Targeted drug-aerosol delivery in the human respiratory system. Annu Rev Biomed Eng. 2008;10: 195–220. | ||
Plank C. Nanomagnetosols: magnetism opens up new prespectives for targeted aerosol delivery to the lung. Trends Biotechnol. 2008;26(2):59–63. | ||
Dames P, Gleich B, Flemmer A, et al. Targeted delivery of magnetic aerosol droplets to the lung. Nat Nanotechnol. 2007;2(8):495–499. | ||
Brain JD, Bloom SB, Valberg PA, Gehr P. Correlation between the behavior of magnetic iron oxide particles in the lungs of rabbits and phagocytosis. Exp Lung Res. 1984;6(2):115–131. | ||
Bellin MF. MR contrast agents, the old and the new. Eur J Radiol. 2006;60(3):314–323. | ||
Saito K, Shindo H, Ozuki T, et al. Perfusion study of hypervascular hepatocellular carcinoma with SPIO. Magn Reson Med Sci. 2005;4(4):151–158. | ||
Vehring R. Pharmaceutical particle engineering via spray drying. Pharm Res. 2008;25(5):999–1022. | ||
Tewes F, Ehrhardt C, Healy AM. Superparamagnetic iron oxide nanoparticles (SPIONs)-loaded Trojan microparticles for targeted aerosol delivery to the lung. Eur J Pharm Biopharm. 2014;86(1):98–104. | ||
Lee WL, Guo WM, Ho VHB, et al. Inhibition of 3-d tumor spheroids by timed-released hydrophilic and hydrophobic drugs from multilayered polymeric microparticles. Small. 2014;10(19):3986–3996. | ||
Xie Y, Longest PW, Xu YH, Wang JP, Wiedmann TS. In vitro and in vivo lung deposition of coated magnetic aerosol particles. J Pharm Sci. 2010;99(11):4658–4668. | ||
Redman GES, Martin AR, Waszak P, et al. Pilot study of inhaled aerosols targeted via magnetic alignment of high aspect ratio particles in rabbits. J Nanomater. 2011;2011:1–7. | ||
Xi J, Zhang Z, Si X. Improving intranasal delivery of neurological nanomedicine to the olfactory region using magnetophoretic guidance of microsphere carriers. Int J Nanomedicine. 2015;10:1211–1222. | ||
Pourmhran O, Rahimi-Gorji M, Gorji-Bandpy M, Gorji TB. Simulation of magnetic drug targeting through tracheobronchial airways in the presence of an external non-uniform magnetic field using Lagrangian magnetic particle tracking. J Magn Magn Mater. 2015;393:380–393. | ||
Martinez RC, Roshchenko A, Minev P, Finlay WH. Simulation of enhanced deposition due to magnetic field alignment of ellipsoidal particles in a lung bifurcation. J Aerosol Med Pulm Drug Deliv. 2013;26(1):31–40. | ||
Ochs M, Nyengaard JR, Jung A, et al. The number of alveoli in the human lung. Am J Respir Crit Care Med. 2004;169(1):120–124. | ||
Haefeli-Bleuer B, Weibel ER. Morphometry of the human pulmonary acinus. Anat Rec. 1988;220(4):401–414. | ||
Krafcik A, Babinec P, Frollo I. Computational analysis of magnetic field induced deposition of magnetic particles in lung alveolus in comparison to deposition produced with viscous drag and gravitational force. J Magn Magn Mater. 2015;380:46–53. | ||
Sznitman J, Heimsch T, Wildhaber JH, Tsuda A, Rösgen T. Respiratory flow phenomena and gravitational deposition in a three-dimensional space-filling model of the pulmonary acinar tree. J Biomech Eng. 2009;131(3):031010. | ||
Hofemeier P, Sznitman J. Role of alveolar topology on acinar flows and convective mixing. J Biomech Eng. 2014;136(6):061007. | ||
Hofemeier P, Sznitman J. Revisiting pulmonary acinar particle transport: convection, sedimentation, diffusion, and their interplay. J Appl Physiol. 2015;118(11):1375–1385. | ||
Linhartová A, Caldwell W, Anderson AE. A proposed alveolar model for adult human lungs: the regular dodecahedron. Anat Rec. 1986;214(3):266–272. | ||
Kumar H, Vasilescu DM, Yin Y, Hoffman EA, Tawhai MH, Lin CL. Multiscale imaging and registration-driven model for pulmonary acinar mechanics in the mouse. J Appl Physiol. 2013;114(8):971–978. | ||
Fung YC. A model of the lung structure and its validation. J Appl Physiol. 1988;64(5):2132–2141. | ||
Khajeh-Hosseini-Dalasm N, Longest PW. Deposition of particles in the alveolar airways: inhalation and breath-hold with pharmaceutical aerosols. J Aerosol Sci. 2015;79:15–30. | ||
Jahani N, Yin Y, Hoffman EA, Lin CL. Assessment of regional non-linear tissue deformation and air volume change of human lungs via image registration. J Biomech. 2014;47(7):1626–1633. | ||
Hofemeier P, Fishler R, Sznitman J. The role of respiratory flow asynchrony on convective mixing in the pulmonary acinus. Fluid Dyn Res. 2014;46(4):1–16. | ||
Gil J, Bachofen H, Gehr P, Weibel ER. Alveolar volume-surface area relation in air- and saline-filled lungs fixed by vascular perfusion. J Appl Physiol Respir Environ Exerc Physiol. 1979;47(5):990–1001. | ||
Sznitman J, Heimsch F, Heimsch T, Rusch D, Rösgen T. Three-dimensional convective alveolar flow induced by rhythmic breathing motion of the pulmonary acinus. J Biomech Eng. 2007;129(5):658–665. | ||
Sznitman J. Respiratory microflows in the pulmonary acinus. J Biomech. 2013;46(2):284–298. | ||
ANSYS® Academic Research, Release 15.0, Help System, Ansys Fluent Theory Guide, ANSYS, Inc. 2011. | ||
Ounis H, Ahmadi G, McLaughlin JB. Brownian diffusion of submicrometer particles in the viscous sublayer. J Colloid Interface Sci. 1991;143(1):266–277. | ||
Haverkort JW, Kenjereš S, Kleijn CR. Computational simulations of magnetic particle capture in arterial flows. Ann Biomed Eng. 2009;37(12):2436–2448. | ||
Xu H, Song T, Bao X, Hu L. Site-directed research of magnetic nanoparticles in magnetic drug targeting. J Magn Magn Mater. 2005;293(1):514–519. | ||
Nacev A. Magnetic drug targeting: developing the basics. [phD thesis]. Graduate School the of University of Maryland, College Park, MD, USA. 2013. | ||
Nacev A, Kim SH, Rodriguez-Canales J, Tangrea M, Shapiro B, Emmert-Buck MR. A dynamic magnetic shift method to increase nanoparticle concentration in cancer metastases: a feasibility study using simulations on autopsy specimens. Int J Nanomedicine. 2011;6:2907–2923. | ||
Alexiou C, Diehl D, Henninger P, et al. A high field gradient magnet for magnetic drug targeting. IEEE Trans Appl Supercond. 2006;16(2):1527–1530. | ||
Li T, Kheifets S, Medellin D, Raizen MG. Measurement of the instantaneous velocity of a Brownian particle. Science. 2010;328(5986):1673–1675. | ||
Kojic M, Tsuda A. A simple model for gravitational deposition of non-diffusing particles in oscillatory laminar pipe flow and its application to small airways. J Aerosol Sci. 2004;35(2):245–261. | ||
Brosh T, Kalman H, Levy A. Accelerating CFD–DEM simulation of processes with wide particle size distributions. Particuology. 2014;12:113–121. | ||
ICRP Protection International Commission on Radiological. Human respiratory tract model for radiological protection. ICRP publication 66. Ann ICRP. 1994;24(1–3):1–482. | ||
Tenenbaum Katan J, Hofemeier P, Sznitman J. Computational models of inhalation therapy in early childhood: therapeutic aerosols in the developing acinus. J Aerosol Med Pulm Drug Deliv. Epub 2016 Feb 23. | ||
Velkov T, Abdul Rahim N, Zhou QT, Chan H-K, Li J. Inhaled anti-infective chemotherapy for respiratory tract infections: successes, challenges and the road ahead. Adv Drug Deliv Rev. 2015;85:65–82. |
 © 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.
© 2016 The Author(s). This work is published and licensed by Dove Medical Press Limited. The full terms of this license are available at https://www.dovepress.com/terms.php and incorporate the Creative Commons Attribution - Non Commercial (unported, v3.0) License.
By accessing the work you hereby accept the Terms. Non-commercial uses of the work are permitted without any further permission from Dove Medical Press Limited, provided the work is properly attributed. For permission for commercial use of this work, please see paragraphs 4.2 and 5 of our Terms.